了解噪声的含义、添加位置以及噪声对效果衡量工作的影响。
摘要报告是对可汇总报告进行汇总的结果。 当收集器对可汇总报告进行批处理并由汇总服务处理时,生成的摘要报告中会添加噪声(随机数量的数据)。 系统会添加噪声,以保护用户隐私。此机制的目标是拥有一个可以支持差分隐私衡量的框架。
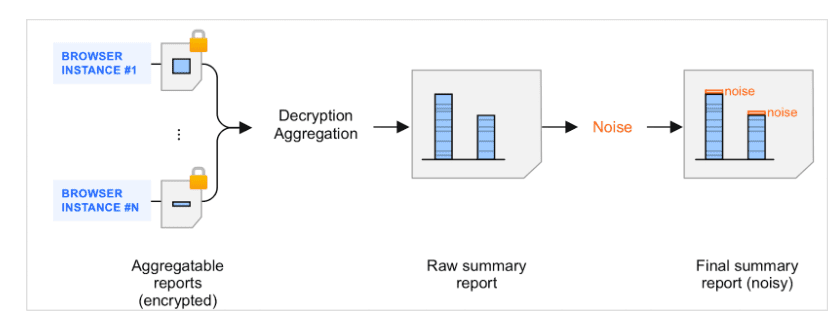
摘要报告中的噪声简介
虽然目前在广告效果衡量中通常不会添加噪声,但在很多情况下,添加噪声不会显著改变您对结果的解读方式。
您不妨从以下几个方面进行思考: 如果数据并不杂乱,您是否有信心根据这些数据做出决策?
例如,假设广告系列 A 获得了 15 次转化,广告系列 B 获得了 16 次转化,广告客户是否有信心改变其广告系列策略或预算?
如果答案是否定的,则表示噪声不相关。
您需要按如下方式配置 API 使用:
- 上述问题的答案是“是”。
- 管理噪声的方式不会显著影响您根据特定数据做出决策的能力。您可以按以下步骤操作:对于预期的最低转化次数,您希望将所收集指标中的噪声保持在一定百分比以下。
在本节和后续内容中,我们将概述实现 2.
核心概念
每次请求摘要报告时,汇总服务都会向每个摘要值添加一次噪声(即每个键添加一次)。
这些噪声值是从特定概率分布中随机抽取的,如下所述。
所有影响噪声的元素都依赖于两个主要概念。
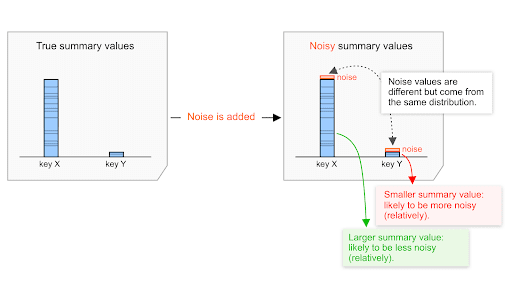
无论汇总值是低值还是高值,噪声分布情况(详情如下)都相同。因此,摘要值越高,噪声的影响(相对于此值)可能越小。
例如,假设总购买总价值 2 万美元和总购买总价值 200 美元都受到了从同一分布中选择的噪声的影响。
我们假设此分布的噪音变化大约在 -100 到 +100 之间。
- 对于 20,000 美元的摘要购买价值,噪声介于 0 和 100/20,000=0.5% 之间。
- 对于 200 美元的汇总购买价值,噪声介于 0 和 100/200=50% 之间。
因此,噪声对 2 万美元的总购买价值的影响可能低于 200 美元。相对而言,20,000 美元可能不太嘈杂,因为信噪比可能会更高。
这有一些重要的实际影响,将在下一部分概述。此机制是 API 设计的一部分,其实际影响是长期的。在广告技术平台设计和评估各种汇总策略时,它们将继续发挥重要作用。
虽然无论汇总值如何,噪声都是从同一分布中提取的,但该分布取决于多个参数。在已结束的来源试验中,广告技术平台可以更改其中一个参数 epsilon,以评估各种效用/隐私调整。但是,将 Epsilon 调整能力视为临时性。我们欢迎您就自己的用例和效果良好的 Epsilon 值提供反馈。
虽然广告技术公司无法直接控制噪声的添加方式,但可能会影响噪声对衡量数据的影响。在接下来的部分中,我们将深入探讨在实践中噪声如何影响。
在开始之前,我们先来详细了解一下噪声应用方式。
放大:如何应用噪声
单一噪声分布
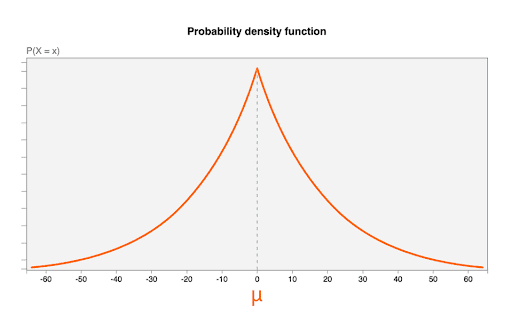
噪声是从拉普拉斯分布中提取的,包含以下参数:
- 平均值 (
μ) 为 0。这意味着最可能的噪声值为 0(未添加噪声),并且噪声值既可能小于原始值,也可能小于原始值(有时称为“无偏见”)。 - scale 参数为
b = CONTRIBUTION_BUDGET/epsilon。CONTRIBUTION_BUDGET是在浏览器中定义的。epsilon在汇总服务器中已修复。
下图显示了 μ=0、b = 20 时拉普拉斯分布的概率密度函数:
随机噪声值,一个噪声分布
假设广告技术平台请求获取两个汇总键(key1 和 key2)的摘要报告。
汇总服务会遵循相同的噪声分布选择两个噪声值 x1 和 x2。将 x1 添加到 key1 的汇总值中,并将 x2 添加到 key2 的汇总值中。
在图中,我们将噪声值表示为相同值。这是一种简化:实际上,噪声值会有所不同,因为它们是从分布中随机抽取的。
这说明噪声值均来自相同的分布,并且独立于它们所应用到的摘要值。
噪声的其他属性
噪声将应用于每个摘要值,包括空值 (0)。
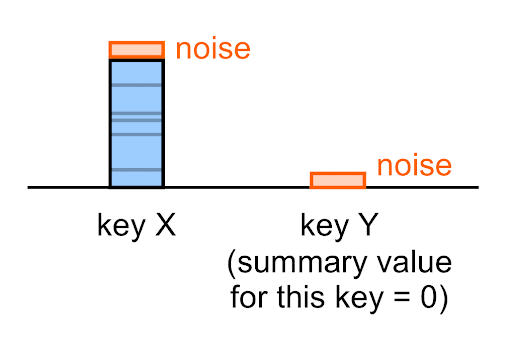
例如,即使给定键的真实摘要值为 0,您在该键的摘要报告中看到的噪声摘要值(极有可能)也不会为 0。
噪声可以是正数或负数。
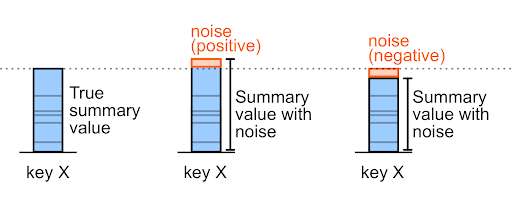
例如,对于噪声前的购买交易金额 327,000,噪声可以是 +6,000 或 -6,000(这些是任意示例值)。
正在评估噪声
计算噪声的标准差
噪声的标准差为:
b*sqrt(2) = (CONTRIBUTION_BUDGET / epsilon)*sqrt(2)
示例
当 Epsilon 值为 10 时,噪声的标准偏差为:
b*sqrt(2) = (CONTRIBUTION_BUDGET / epsilon)*sqrt(2) = (65,536/10)*sqrt(2) = 9,267
评估衡量结果出现显著差异的情况
由于您将知道汇总服务向每个输出值添加的噪声的标准差,因此可以确定适当的阈值进行比较,以确定观察到的差异是否可能由噪声所致。
例如,如果添加到值中的噪声约为 +/- 10(考虑到缩放),并且两个广告系列之间的值差超过 100,那么我们很有可能会得出以下结论:每个广告系列之间测量的值的差异并非仅由噪声所致。
互动和分享反馈
您可以参与试用并试用此 API。
- 了解可汇总报告和汇总服务,提出问题并提出反馈。
- 阅读归因报告指南。
- 在 Privacy Sandbox 开发者支持代码库中提问并加入讨论。
后续步骤
- 如需了解您可以控制哪些变量来提高信噪比,请参阅处理噪声。
- 查看根据摘要报告设计决策进行实验,获取有关规划汇总报告策略的帮助。
- 不妨试试 Noise 实验室。

