Bu sayfada Karar Ağaçları sözlük terimleri yer almaktadır. Tüm terimler için burayı tıklayın.
A
özellik örnekleme
Her karar ağacının koşulu öğrenirken yalnızca olası özelliklerden rastgele bir alt kümeyi dikkate aldığı bir karar ormanı eğitme taktiği. Genellikle her düğüm için farklı bir özellik alt kümesi örneklenir. Buna karşılık, özellik örnekleme olmadan bir karar ağacı eğitilirken her düğüm için olası tüm özellikler dikkate alınır.
eksenle hizalanmış koşul
Karar ağacında yalnızca tek bir özelliği içeren koşul. Örneğin, area bir özellikse aşağıdaki koşul eksene göre hizalanmış bir koşuldur:
area > 200
Eğik koşul ile karşılaştırın.
B
paketleme
Her bileşen modelinin, yerine örneklemeyle rastgele bir eğitim örneği alt kümesinde eğitildiği bir toplu eğitme yöntemi. Örneğin, rastgele orman, torba oluşturma yöntemiyle eğitilmiş karar ağaçlarının bir koleksiyonudur.
Bagging terimi, bootstrap aggregating ifadesinin kısaltmasıdır.
Daha fazla bilgi için Karar Ağaçları kursunda Rastgele ormanlar bölümüne bakın.
ikili koşul
Karar ağacında, genellikle evet veya hayır olmak üzere yalnızca iki olası sonucu olan koşul. Örneğin, aşağıdakiler ikili koşuldur:
temperature >= 100
Non-binary koşulu ile karşılaştırın.
Daha fazla bilgi için Karar Ağaçları kursunda Koşul türleri bölümüne bakın.
C
koşul
Karar ağacında, bir ifadeyi değerlendiren tüm düğümler. Örneğin, bir karar ağacının aşağıdaki kısmı iki koşul içerir:
Koşullara gruplandırma veya test denir.
Yaprak ile kontrast koşulu.
Şuna da bakabilirsiniz:
Daha fazla bilgi için Karar Ağaçları kursunda Koşul türleri bölümüne bakın.
D
karar ormanı
Birden fazla karar ağacından oluşturulmuş bir model. Karar ormanı, karar ağaçlarının tahminlerini toplayarak tahmin yapar. Popüler karar ağacı türleri arasında rastgele ormanlar ve gradyan artırmalı ağaçlar yer alır.
Daha fazla bilgi için Karar Ağaçları kursunun Karar Ağaçları bölümüne bakın.
karar ağacı
Hiyerarşik olarak düzenlenmiş bir dizi koşul ve yaprak içeren denetimli bir öğrenme modeli. Örneğin, aşağıdaki bir karar ağacıdır:
E
entropi
Bilgi teorisinde, olasılık dağılımının ne kadar tahmin edilemez olduğunun açıklaması. Alternatif olarak entropi, her örnek'in ne kadar bilgi içerdiği olarak da tanımlanır. Bir rastgele değişkenin tüm değerlerinin olasılığı eşit olduğunda dağılım mümkün olan en yüksek entropi değerine sahiptir.
"0" ve "1" olmak üzere iki olası değere sahip bir kümenin entropisi (örneğin, ikili sınıflandırma problemindeki etiketler) aşağıdaki formüle sahiptir:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
Bu örnekte:
- H entropidir.
- p, "1" örneklerinin kesridir.
- q, "0" örneklerinin kesridir. q = (1 - p) olduğunu unutmayın.
- log genellikle log2'dir. Bu durumda entropi birimi bittir.
Örneğin, aşağıdakileri varsayalım:
- 100 örnek "1" değerini içerir
- 300 örnek "0" değerini içeriyor
Bu nedenle, entropi değeri:
- p = 0,25
- q = 0,75
- H = (-0,25)log2(0,25) - (0,75)log2(0,75) = örnek başına 0,81 bit
Mükemmel şekilde dengelenmiş bir kümenin (örneğin, 200 "0" ve 200 "1") örnek başına entropisi 1,0 bit olur. Bir veri kümesi dengeli olmaktan uzaklaştıkça entropisi 0, 0'a doğru hareket eder.
Karar ağaçlarında entropi, sınıflandırma karar ağacının büyümesi sırasında ayırıcı'nın koşulları seçmesine yardımcı olmak için bilgi kazancı oluşturmaya yardımcı olur.
Entropiyi şu verilerle karşılaştırın:
- gini impurity
- çapraz entropi kayıp işlevi
Entropi genellikle Shannon entropisi olarak adlandırılır.
Daha fazla bilgi için Karar Ağaçları kursunda Sayısal özelliklere sahip ikili sınıflandırma için tam bölücü bölümüne bakın.
C
özellik önem düzeyleri
Değişken önemleri için eş anlamlı.
G
gini safsızlık
Entropy'ye benzer bir metrik. Bölücüler, sınıflandırma karar ağaçları için koşullar oluşturmak amacıyla gini safsızlık veya entropi değerlerinden türetilen değerleri kullanır. Bilgi kazancı entropi temellidir. Gini safsızlıktan türetilen metrik için evrensel olarak kabul edilen eşdeğer bir terim yoktur. Ancak bu adsız metrik, bilgi kazancı kadar önemlidir.
Gini safsızlık oranı, gini endeksi veya kısaca gini olarak da adlandırılır.
gradyan artırımlı (karar) ağaçları (GBT)
Aşağıdaki özelliklere sahip bir karar ormanı türü:
- Eğitim, gradyan güçlendirme yöntemini kullanır.
- Zayıf model bir karar ağacıdır.
Daha fazla bilgi için Karar Ağaçları kursunda Gradyan Destekli Karar Ağaçları bölümüne bakın.
gradyan güçlendirme
Zayıf modellerin, güçlü bir modelin kalitesini iteratif olarak iyileştirmek (kaybını azaltmak) için eğitildiği bir eğitim algoritması. Örneğin, doğrusal veya küçük bir karar ağacı modeli zayıf bir model olabilir. Güçlü model, daha önce eğitilmiş tüm zayıf modellerin toplamı olur.
Gradyan artırmanın en basit biçiminde, her iterasyonda zayıf bir model, güçlü modelin kayıp gradyanını tahmin edecek şekilde eğitilir. Ardından, güçlü modelin çıkışı, gradyan azalma'ya benzer şekilde tahmin edilen gradyan çıkarılarak güncellenir.
Bu örnekte:
- $F_{0}$, başlangıçtaki güçlü modeldir.
- $F_{i+1}$, bir sonraki güçlü modeldir.
- $F_{i}$, mevcut güçlü modeldir.
- $\xi$, 0,0 ile 1,0 arasında bir değerdir ve küçültme olarak adlandırılır. Bu değer, gradyan azalmadaki öğrenme hızına benzer.
- $f_{i}$, $F_{i}$ değerinin kayıp gradyantını tahmin etmek için eğitilmiş zayıf modeldir.
Gradyan artırmanın modern varyasyonları, hesaplamalarında kaybın ikinci türevini (Hessian) de içerir.
Karar ağaçları, gradyan artırmada genellikle zayıf modeller olarak kullanılır. Gradyan artırılmış (karar) ağaçları başlıklı makaleyi inceleyin.
I
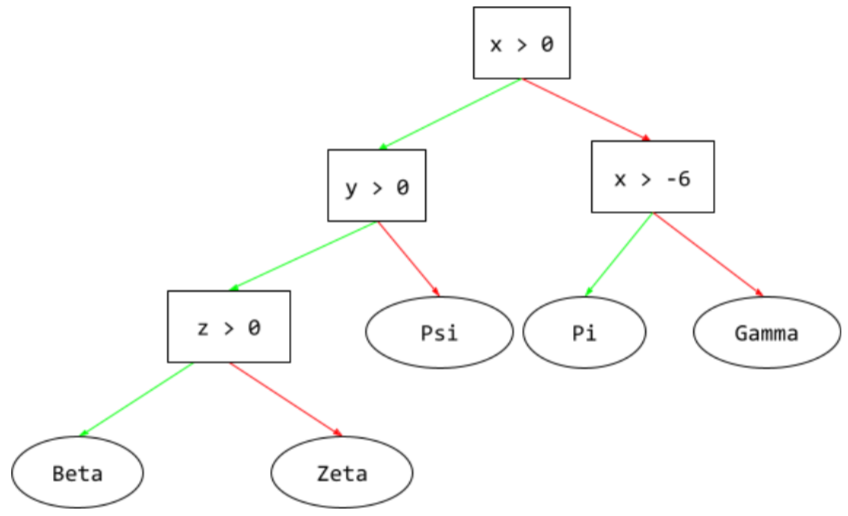
çıkarım yolu
Karar ağacında, çıkarım sırasında belirli bir örnek, kökten diğer koşullara giden ve yaprak ile sona eren yolu takip eder. Örneğin, aşağıdaki karar ağacında daha kalın oklar, aşağıdaki özellik değerlerine sahip bir örnek için çıkarım yolunu gösterir:
- x = 7
- y = 12
- z = -3
Aşağıdaki görselde gösterilen çıkarım yolu, yaprağa (Zeta) ulaşmadan önce üç koşuldan geçer.
Üç kalın ok, çıkarım yolunu gösterir.
Daha fazla bilgi için Karar Ağaçları kursundaki Karar ağaçları bölümüne bakın.
bilgi kazancı
Karar ağaçlarında, bir düğümün entropisi ile alt düğümlerinin entropisinin ağırlıklı (örnek sayısına göre) toplamı arasındaki farktır. Bir düğümün entropisi, söz konusu düğümdeki örneklerin entropisidir.
Örneğin, aşağıdaki entropi değerlerini ele alalım:
- Üst düğümün entropisi = 0,6
- 16 alakalı örnek içeren bir alt düğümün entropisi = 0,2
- 24 alakalı örnek içeren başka bir alt düğümün entropisi = 0,1
Dolayısıyla örneklerin% 40'ı bir alt düğümde, %60'ı ise diğer alt düğümdedir. Bu nedenle:
- Alt düğümlerin ağırlıklı entropi toplamı = (0,4 * 0,2) + (0,6 * 0,1) = 0,14
Bilgi kazancı şu şekildedir:
- bilgi kazancı = üst öğenin entropisi - alt öğelerin ağırlıklı entropi toplamı
- bilgi kazancı = 0,6 - 0,14 = 0,46
Çoğu bölen, bilgi kazanımını en üst düzeye çıkaran koşullar oluşturmaya çalışır.
ayar içinde koşul
Karar ağacında, bir öğe grubunda bir öğenin bulunup bulunmadığını test eden koşul. Örneğin, aşağıdakiler grup içi koşuldur:
house-style in [tudor, colonial, cape]
Çıkarımda, ev stili özelliğinin değeri tudor veya colonial veya cape ise bu koşul Evet olarak değerlendirilir. Ev stili özelliğinin değeri başka bir şeyse (örneğin, ranch) bu koşul Hayır olarak değerlendirilir.
Set içi koşullar genellikle tek sıcak kodlu özellikleri test eden koşullardan daha verimli karar ağaçlarına yol açar.
L
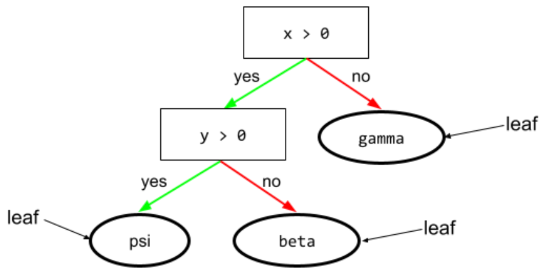
yaprak
Karar ağacındaki herhangi bir uç nokta. Koşul'un aksine, yaprak bir test gerçekleştirmez. Bunun yerine, bir yaprak olası bir tahmindir. Yapraklar, çıkarım yolunun terminal düğümüdür.
Örneğin, aşağıdaki karar ağacı üç yaprak içerir:
H
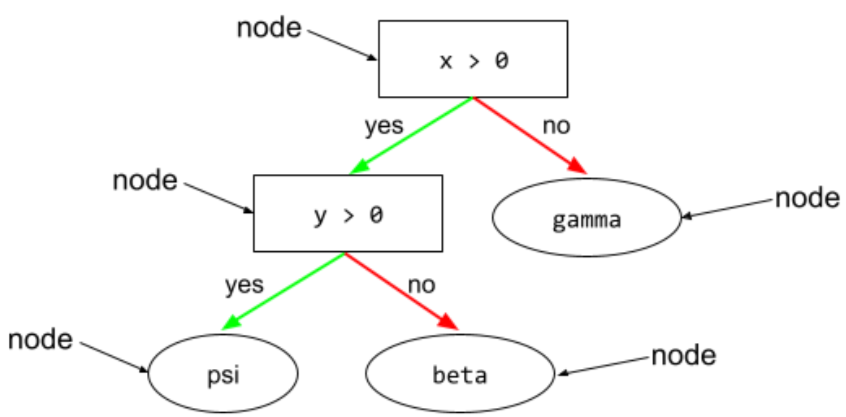
düğüm (karar ağacı)
Karar ağacında koşul veya yaprak.
diğer durum
İkiden fazla olası sonuç içeren bir koşul. Örneğin, aşağıdaki ikili olmayan koşul üç olası sonuç içerir:
O
eğik koşul
Karar ağacında, birden fazla özellik içeren koşul. Örneğin, yükseklik ve genişlik her ikisi de özellikse aşağıdaki koşul eğik koşuldur:
height > width
Ekseni hizalama koşuluyla karşılaştırın.
paket dışı değerlendirme (OOB değerlendirme)
Her karar ağacını, söz konusu karar ağacının eğitimi sırasında kullanılmayan örneklerle test ederek karar ormanı kalitesini değerlendirme mekanizması. Örneğin, aşağıdaki şemada sistemin her karar ağacını örneklerin yaklaşık üçte ikisinde eğittiğini ve ardından örneklerin kalan üçte birinde değerlendirdiğini görebilirsiniz.
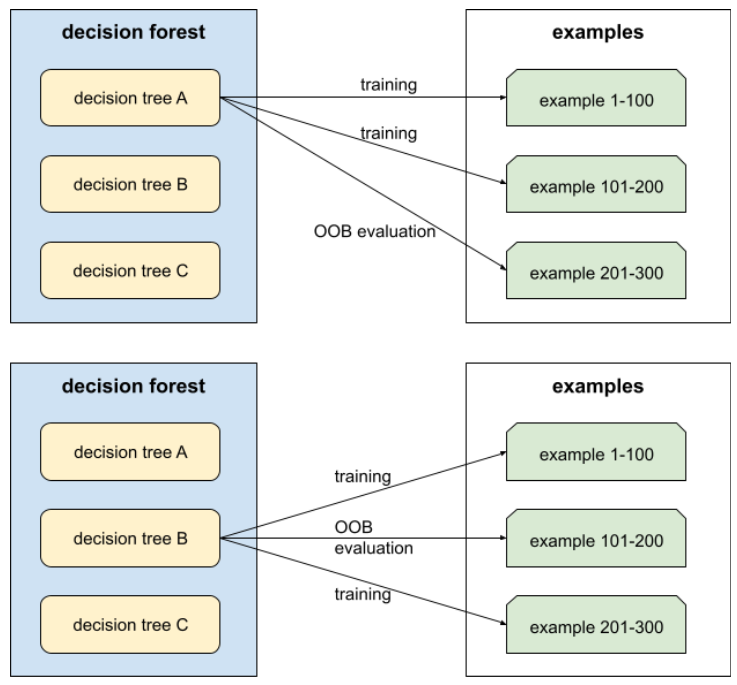
Paket dışı değerlendirme, çapraz doğrulama mekanizmasının hesaplama açısından verimli ve muhafazakar bir yaklaşımıdır. Çapraz doğrulamada her çapraz doğrulama turu için bir model eğitilir (örneğin, 10 kat çapraz doğrulamada 10 model eğitilir). Hariç tutulan veri kümesi değerlendirmesinde tek bir model eğitilir. Toplama, eğitim sırasında her ağaçtan bazı verileri atladığı için, harici veri kümesi değerlendirmesi, çapraz doğrulamayı yaklaşık olarak belirlemek için bu verileri kullanabilir.
P
permütasyon değişkeni önemleri
Özelliğin değerlerini permütasyona tabi tuttuktan sonra bir modelin tahmin hatasındaki artışı değerlendiren bir değişken önemi türü. Permütasyon değişkeni önemi, modelden bağımsız bir metriktir.
K
rastgele orman
Her karar ağacının bagging gibi belirli bir rastgele gürültüyle eğitildiği karar ağaçlarından oluşan bir toplu.
Rastgele ormanlar, bir tür karar ormanı'dır.
kök
Karar ağacındaki başlangıç düğümü (ilk koşul). Kural olarak, diyagramlarda kök karar ağacının en üstüne yerleştirilir. Örneğin:
S
Değiştirmeyle örnekleme
Aynı öğenin birden çok kez seçilebileceği bir aday öğe grubundan öğe seçme yöntemi. "Yenilemeli" ifadesi, her seçimden sonra seçilen öğenin, aday öğe havuzuna iade edildiği anlamına gelir. Ters yöntem olan yerine koyma olmadan örnekleme, bir aday öğenin yalnızca bir kez seçilebileceği anlamına gelir.
Örneğin, aşağıdaki meyve grubunu ele alalım:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Sistemin ilk öğe olarak rastgele fig seçtiğini varsayalım.
Değişimli örnekleme kullanılıyorsa sistem aşağıdaki gruptan ikinci öğeyi seçer:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Evet, bu öncekiyle aynı grup. Dolayısıyla sistem fig'ü tekrar seçebilir.
Örnekleme işleminde değiştirme yapılmazsa seçilen bir örnek tekrar seçilemez. Örneğin, sistem ilk örnek olarak rastgele fig'ü seçerse fig tekrar seçilemez. Bu nedenle sistem, ikinci örneği aşağıdaki (azaltılmış) kümeden seçer:
fruit = {kiwi, apple, pear, cherry, lime, mango}küçülme
Gradyan güçlendirme'de aşırı uyumu kontrol eden bir hiperparametre. Gradyan artırmada küçülme, gradyan inişindeki öğrenme hızına benzer. Shrinkage, 0,0 ile 1,0 arasında bir ondalık değerdir. Daha düşük bir küçülme değeri, daha yüksek bir küçülme değerinden daha fazla aşırı uyumu azaltır.
Split
Karar ağacında koşul için kullanılan başka bir ad.
ayırıcı
Bir karar ağacı eğitilirken her düğümde en iyi koşulu bulmakla görevli rutin (ve algoritma).
T
test
Karar ağacında koşul için kullanılan başka bir ad.
eşik (karar ağaçları için)
Ekseni hizalanmış koşulda, özelliğin karşılaştırıldığı değerdir. Örneğin, aşağıdaki koşulda eşik değer 75'tir:
grade >= 75
V
değişken önemleri
Her bir özelliğin modele göreli önemini gösteren bir puan grubu.
Örneğin, ev fiyatlarını tahmin eden bir karar ağacını düşünün. Bu karar ağacında üç özellik kullanıldığını varsayalım: beden, yaş ve stil. Üç özellik için değişken önem değerleri {beden=5,8, yaş=2,5, stil=4,7} olarak hesaplanırsa beden, karar ağacı için yaş veya stilden daha önemlidir.
ML uzmanlarını modellerin farklı yönleri hakkında bilgilendirebilecek farklı değişken önemi metrikleri vardır.
W
kitlenin bilgeliği
Büyük bir grup insanın ("kalabalık") görüşlerinin veya tahminlerinin ortalamasının genellikle şaşırtıcı derecede iyi sonuçlar verdiği fikri. Örneğin, kullanıcıların büyük bir kavanoza doldurulmuş jöle fasulyesi sayısını tahmin ettiği bir oyun düşünün. Çoğu tahmin yanlış olsa da tüm tahminlerin ortalamasının, kavanozdaki jelibon sayısının gerçek değerine şaşırtıcı derecede yakın olduğu deneysel olarak gösterilmiştir.
Ensembler, kitlenin bilgeliğinin yazılımdaki karşılığıdır. Tek tek modeller çok yanlış tahminler yapsa bile birçok modelin tahminlerinin ortalaması genellikle şaşırtıcı derecede iyi tahminler verir. Örneğin, tek bir karar ağacı kötü tahminler yapabilir ancak karar ormanı genellikle çok iyi tahminler yapar.