Sayısal özelliklere sahip ikili sınıflandırma için tam ayırıcı

Bu ünitede, aşağıdaki ayarda $\mathrm{feature}_i \geq t$ biçiminde koşullar oluşturan en basit ve en yaygın ayırıcı algoritmasını keşfedeceksiniz:

• İkili program sınıflandırma görevi
• Örneklerde değerler eksik
• Örneklerde önceden hesaplanmış dizin olmadan

Sayısal bir özellik ve ikili etiket içeren "turuncu" ve "mavi" şeklinde bir dizi $n$ örneği varsayalım. $D$ veri kümesini şu şekilde açıklayabiliriz:

$$D = \{(x_i,y_i)\}_{i\in[1,n]}$$

Bu örnekte:

• $x_i$, $\mathbb{R}$ cinsinden sayısal bir özelliğin değeridir (gerçek sayılar grubu).
• $y_i$, {orange, blue} cinsinden ikili sınıflandırma etiketi değeridir.

Amacımız, $D$ (eşik) değerini, $x_i \geq t$ koşuluna göre $D(rue)$ ve $F(alse)$ gruplarına bölmek ile etiketlerin ayrılmasını iyileştirmek için bir eşik değeri bulmaktır. Örneğin, $T$ ve diğer kaynaklardaki $o{0}turuncu" daha fazla örnek

Shannon entropisi bir bozukluk ölçüsüdür. İkili etiket için:

• Shannon entropi, örneklerdeki etiketler dengeli olduğunda maksimum düzeydedir (%50 mavi ve% 50 turuncu).
• Shannon entropi, örneklerdeki etiketler saf (%100 mavi veya% 100 turuncu) olduğunda minimum düzeydedir (sıfır değerinde).

8. Şekil. Üç farklı entropi seviyesi.

 

Resmî olarak, $T$ ve $F$ arasındaki etiket dağıtımlarının entropilerinin ağırlıklı toplamını azaltan bir koşul bulmak istiyoruz. Buna karşılık, bilgi kazancı $$$, <$$tr, tr-TR$ arasındaki farktır. Bu farka bilgi edinme denir.

Aşağıdaki şekilde, entropi yüksek kalırken bilgiler düşük olan kötü bir dağılım gösterilmektedir:

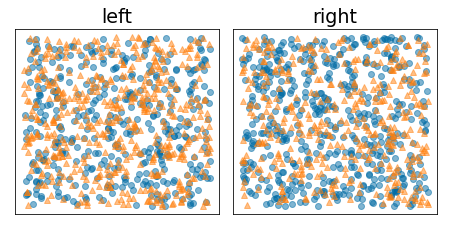
9. Şekil. Kötü bölme, etiketin entropisini azaltmaz.

 

Buna karşılık, aşağıdaki şekilde entropi düşük olduğunda (ve bilgi arttığında) daha iyi bir dağılım görülmektedir:

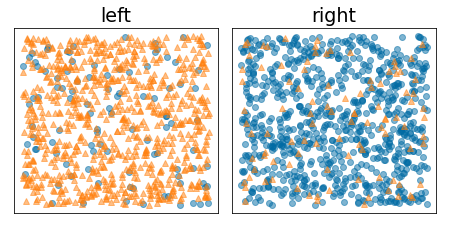
Şekil 10. İyi bir bölme, etiketin entropisini azaltır.

 

Resmi olarak:

\[\begin{eqnarray} T & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \ge t \} \\[12pt] F & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \lt t \} \\[12pt] R(X) & = & \frac{\lvert \{ x | x \in X \ \textrm{and} \ x = \mathrm{pos} \} \rvert}{\lvert X \rvert} \\[12pt] H(X) & = & - p \log p - (1 - p) \log (1-p) \ \textrm{with} \ p = R(X)\\[12pt] IG(D,T,F) & = & H(D) - \frac {\lvert T\rvert} {\lvert D \rvert } H(T) - \frac {\lvert F \rvert} {\lvert D \rvert } H(F) \end{eqnarray}\]

Bu örnekte:

• $IG(D,T,F)$, $D$'ı $T$ ve $F$ olarak ikiye bölerek elde edilen bilgi kazancıdır.
• $H(X)$, $X$ örnek grubunun entropisidir.
• $|X|$, $X$ kümesindeki öğelerin sayısıdır.
• Eşik, $t$ değeridir.
• $pos$, pozitif etiket değeridir. Örneğin, yukarıdaki örnekte "blue" "Pozitif etiket" olarak farklı bir etiket seçilmesi, entropi değerini veya bilgi kazancını değiştirmez.
• $R(X)$, $X$ örneklerindeki pozitif etiket değerlerinin oranıdır.
• $D$, bu veri kümesinde olduğu gibi veri kümesidir.

Aşağıdaki örnekte, tek bir sayısal özellik olan $x$ değerine sahip bir ikili sınıflandırma veri kümesi değerlendirilmektedir. Aşağıdaki şekilde, farklı eşik $t$ değerleri (x ekseni) için gösterilmektedir:

1. $x$ özelliğinin histogramı.
2. Eşik değerine göre $D$, $T$ ve $F$ setlerindeki "mavi" örneklerin oranı.
3. $D$, $T$ ve $F$ adlı entropi.
4. Bilgi kazancı; diğer bir deyişle, $D$ ile {$T$,$F$} arasındaki entropi deltası, örnek sayısı tarafından ağırlıklandırılır.

Şekil 11. Dört eşik grafiği.

 

Bu grafiklerde şunlar gösterilir:

• "Sıklık" grafiği, gözlemlerin 18 ile 60 arasındaki konsantrasyonlarla nispeten iyi bir şekilde yayıldığını gösterir. Geniş bir değer dağılımı, modelin eğitilmesi açısından iyi olan çok sayıda potansiyel bölünme olduğu anlamına gelir.

• Veri kümesindeki "mavi" etiketlerinin oranı yaklaşık %25'tir. Mavi etiketin "oranı", 20 ile 50 arasındaki eşik değerleri için şunları gösterir:

  • $T$ grubu, aşırı sayıda "mavi" etiket örneği içeriyor (35. eşik için% 35'e kadar).
  • $F$ grubu, tamamlayıcı "mavi" etiket örnekleri eksikliğini içeriyor (35. eşik için yalnızca% 8).

  Hem mavi etiketlerin "oranı" hem de "entropi" grafikleri, etiketlerin bu eşik aralığında nispeten iyi bir şekilde ayrılabileceğini gösterir.

• Bu gözlem, "bilgi edinme" grafiğinde doğrulanmıştır. Maksimum bilgi edinmenin, yaklaşık 0,074 değerinde bir bilgi edinme değeri için t=28 ile elde edildiğini görüyoruz. Bu nedenle, ayırıcının döndürdüğü koşul $x \geq 28$ olur.

• Bilgi kazancı her zaman pozitif veya değersizdir. Eşik değeri, maksimum / minimum değerine yaklaştıkça sıfıra dönüşür. Bu durumlarda, $F$ veya $T$, diğeri veri kümesinin tamamını içerirken diğeri $D$'dakine benzer bir entropi gösterir. $H(T)$ = $H(F)$ = $H(D)$ olduğunda, ${20&$($) ve ${

Gerçek sayı kümesindeki ($\mathbb{R}$) $t$ için aday değerleri sonsuzdur. Bununla birlikte, verilen örneklerin sayısı sınırlıysa $D$ ve $F$ olarak yalnızca sınırlı sayıda bölüm oluşturulur. Bu nedenle, yalnızca sınırlı sayıda $t$ değeri test edilebilir.

Klasik bir yaklaşım, x_i değerlerini artan x_s(i) sıralamasına göre sıralamaktır. Örneğin:

$$ x_{s(i)} \leq x_{s(i+1)} $$

Daha sonra, arka arkaya sıralanmış $x_i$ değerinin her değeri için $t$ değerini test edin. Örneğin, belirli bir özelliğin 1.000 kayan nokta değerinin olduğunu varsayalım. Sıralamadan sonra ilk iki değerin 8.5 ve 8.7 olduğunu varsayalım. Bu durumda, test edilecek ilk eşik değeri 8,6 olur.

Resmi olarak, t için aşağıdaki aday değerlerini göz önünde bulundururuz:

$$ X = \left\{ \frac {x_{s(i)} + x_{s(i + 1)}} {2} \lvert x_{s(i)} \ne x_{s(i+1)} \right\} $$

Bu algoritmanın zaman karmaşıklığı, $nma ile $\mathcal{O} ( n \log n) $ şeklindedir ve düğümdeki örneklerin sayısıdır (özellik değerlerinin sıralaması nedeniyle). Karar ağacına uygulandığında, ayırıcı düğüm her düğüme ve özelliğe uygulanır. Her düğümün üst örneklerinin yaklaşık 1/2'sini aldığını unutmayın. Dolayısıyla, ana teoreme göre, bu ayırıcıyla bir karar ağacının eğitilmesi zaman alan karmaşıktır:

$$ \mathcal{O} ( m n \log^2 n ) $$

Bu örnekte:

• $m$, özelliklerin sayısıdır.
• $n$, eğitim örneklerinin sayısıdır.

Bu algoritmada, özelliklerin değeri değil, yalnızca sıralama önemlidir. Bu nedenle bu algoritma, özellik değerlerinin ölçeğinden veya dağıtımından bağımsız olarak çalışır. Bu yüzden bir karar ağacı eğitilirken sayısal özellikleri normalleştirmemiz veya ölçeklendirmemiz gerekmez.