מילון מונחים ללמידת מכונה: עקרונות בסיסיים של למידת מכונה

בדף הזה מופיעים מונחים במילון המונחים של ML Fundamentals. כאן אפשר לראות את כל המונחים במילון המונחים.

A

דיוק

#fundamentals

#Metric

מספר התחזיות הנכונות של הסיווג חלקי המספר הכולל של התחזיות. כלומר:

$$\text{Accuracy} = \frac{\text{correct predictions}} {\text{correct predictions + incorrect predictions }}$$

לדוגמה, למודל שביצע 40 חיזויים נכונים ו-10 חיזויים לא נכונים יהיה דיוק של:

$$\text{Accuracy} = \frac{\text{40}} {\text{40 + 10}} = \text{80%}$$

סיווג בינארי מספק שמות ספציפיים לקטגוריות השונות של תחזיות נכונות ותחזיות שגויות. לכן, הנוסחה לחישוב הדיוק בסיווג בינארי היא:

$$\text{Accuracy} = \frac{\text{TP} + \text{TN}} {\text{TP} + \text{TN} + \text{FP} + \text{FN}}$$

where:‎

• ‫TP הוא מספר החיוביים האמיתיים (תחזיות נכונות).
• ‫TN הוא מספר השליליים האמיתיים (חיזויים נכונים).
• ‫FP הוא מספר החיוביים הכוזבים (תחזיות שגויות).
• ‫FN הוא מספר השליליים הכוזבים (תחזיות שגויות).

השוו בין דיוק לבין דיוק והחזרה.

כדי לקבל פרטים על רמת הדיוק ועל מערכי נתונים לא מאוזנים לפי סיווג, לוחצים על הסמל.

למרות שמדובר במדד חשוב במצבים מסוימים, המדד 'דיוק' עלול להטעות מאוד במצבים אחרים. חשוב לציין שדיוק הוא בדרך כלל מדד לא טוב להערכת מודלים של סיווג שמבצעים עיבוד של מערכי נתונים עם חוסר איזון בין המחלקות.

לדוגמה, נניח שבמאה שנה יורד שלג רק ב-25 ימים בעיר סובטרופית מסוימת. מכיוון שמספר הימים ללא שלג (הסיווג השלילי) גדול בהרבה ממספר הימים עם שלג (הסיווג החיובי), מערך הנתונים של השלג בעיר הזו הוא לא מאוזן. תארו לעצמכם מודל של סיווג בינארי שאמור לחזות אם יירד שלג בכל יום, אבל פשוט חוזה שלא יירד שלג בכל יום. המודל הזה מדויק מאוד, אבל אין לו יכולת חיזוי. בטבלה הבאה מסוכמות התוצאות של חיזויים למשך מאה שנה:

קטגוריה	מספר
TP	0
TN	36499
FP	0
FN	25

לכן, רמת הדיוק של המודל הזה היא:

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (0 + 36499) / (0 + 36499 + 0 + 25) = 0.9993 = 99.93%

למרות שרמת דיוק של 99.93% נראית מרשימה מאוד, למודל אין למעשה יכולת חיזוי.

דיוק ורגישות הם בדרך כלל מדדים שימושיים יותר מדיוק להערכת מודלים שאומנו על מערכי נתונים עם חוסר איזון בין המחלקות.

---

מידע נוסף זמין במאמר בנושא סיווג: דיוק, היזכרות, פרסיזיה ומדדים קשורים בסדנה ללמידת מכונה.

פונקציית הפעלה

#fundamentals

פונקציה שמאפשרת לרשתות נוירונים ללמוד קשרים לא ליניאריים (מורכבים) בין תכונות לבין התווית.

פונקציות הפעלה פופולריות כוללות:

• ReLU
• סיגמואיד

הגרפים של פונקציות ההפעלה אף פעם לא קווים ישרים. לדוגמה, הגרף של פונקציית ההפעלה ReLU מורכב משני קווים ישרים:

גרף של פונקציית ההפעלה הסיגמואידית נראה כך:

כדי לראות דוגמה, לוחצים על הסמל.

ברשת נוירונים, פונקציות ההפעלה משנות את הסכום המשוקלל של כל ערכי הקלט לנוירון. כדי לחשב סכום משוקלל, הנוירון מחבר את המכפלות של הערכים והמשקלים הרלוונטיים. לדוגמה, נניח שהקלט הרלוונטי לנוירון מורכב מהנתונים הבאים:

ערך קלט	משקל קלט
2	‫1.3-
-1	0.6
3	0.4

לכן הסכום המשוקלל הוא:

‫

weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0

נניח שהמתכנן של הרשת העצבית הזו בוחר בפונקציית הסיגמואיד כפונקציית ההפעלה. במקרה כזה, הנוירון מחשב את הסיגמואיד של ‎-2.0, שהוא בערך 0.12. לכן, הנוירון מעביר את הערך 0.12 (ולא את הערך ‎-2.0) לשכבה הבאה ברשת העצבית. האיור הבא מציג את החלק הרלוונטי בתהליך:

---

מידע נוסף מופיע במאמר רשתות עצביות: פונקציות הפעלה בסדנה ללימוד מכונת למידה.

לגבי בינה מלאכותית,

#fundamentals

תוכנה או מודל לא אנושיים שיכולים לפתור משימות מורכבות. לדוגמה, תוכנית או מודל שמתרגמים טקסט, או תוכנית או מודל שמזהים מחלות מתמונות רדיולוגיות, שניהם מציגים בינה מלאכותית.

באופן רשמי, למידת מכונה היא תחום משנה של בינה מלאכותית. עם זאת, בשנים האחרונות, חלק מהארגונים התחילו להשתמש במונחים בינה מלאכותית ולמידת מכונה לסירוגין.

AUC (השטח מתחת לעקומת ה-ROC)

#fundamentals

#Metric

מספר בין 0.0 ל-1.0 שמייצג את היכולת של מודל סיווג בינארי להפריד בין סיווגים חיוביים לבין סיווגים שליליים. ככל שערך ה-AUC קרוב יותר ל-1.0, כך יכולת המודל להפריד בין המחלקות טובה יותר.

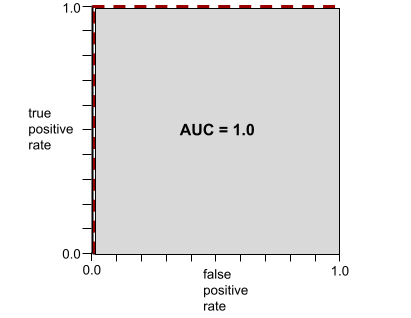
לדוגמה, באיור הבא מוצג מודל סיווג שמפריד בצורה מושלמת בין מחלקות חיוביות (אליפסות ירוקות) לבין מחלקות שליליות (מלבנים סגולים). למודל המושלם הלא-מציאותי הזה יש AUC של 1.0:

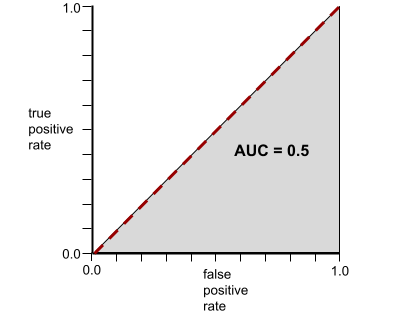
לעומת זאת, באיור הבא מוצגות התוצאות של מודל סיווג שיצר תוצאות אקראיות. למודל הזה יש AUC של 0.5:

כן, למודל הקודם יש AUC של 0.5, ולא 0.0.

רוב הדגמים נמצאים איפשהו בין שני הקצוות. לדוגמה, המודל הבא מפריד בין ערכים חיוביים לשליליים במידה מסוימת, ולכן ערך ה-AUC שלו הוא בין 0.5 ל-1.0:

המדד AUC מתעלם מכל ערך שתגדירו לסף הסיווג. במקום זאת, מדד ה-AUC מתייחס לכל ספי הסיווג האפשריים.

כדי לקבל מידע על הקשר בין AUC לבין עקומות ROC, לוחצים על הסמל.

הערך AUC מייצג את השטח מתחת לעקומת ROC. לדוגמה, עקומת ה-ROC של מודל שמפריד בצורה מושלמת בין ערכים חיוביים לערכים שליליים נראית כך:

ה-AUC הוא השטח של האזור האפור באיור שלמעלה. במקרה החריג הזה, השטח הוא פשוט אורך האזור האפור (1.0) כפול רוחב האזור האפור (1.0). לכן, המכפלה של 1.0 ו-1.0 היא 1.0 בדיוק, שהוא הציון הכי גבוה שאפשר לקבל ב-AUC.

לעומת זאת, עקומת ה-ROC של מודל סיווג שלא יכול להפריד בין מחלקות בכלל נראית כך. שטח האזור האפור הוא 0.5.

עקומת ROC אופיינית יותר נראית בערך כך:

חישוב השטח מתחת לעקומה הזו באופן ידני הוא תהליך מייגע, ולכן בדרך כלל תוכנה מחשבת את רוב ערכי ה-AUC.

---

אפשר ללחוץ על הסמל כדי לראות הגדרה רשמית יותר של AUC.

המדד AUC הוא ההסתברות שמודל סיווג יהיה בטוח יותר שדוגמה חיובית שנבחרה באופן אקראי היא חיובית, מאשר שדוגמה שלילית שנבחרה באופן אקראי היא חיובית.

---

מידע נוסף זמין במאמר בנושא סיווג: ROC ו-AUC בקורס המקוצר על למידת מכונה.

B

backpropagation

#fundamentals

האלגוריתם שמיישם ירידת גרדיאנט ברשתות נוירונים.

אימון של רשת נוירונים כולל הרבה איטרציות של המחזור הבא בן שני השלבים:

1. במהלך המעבר קדימה, המערכת מעבדת אצווה של דוגמאות כדי להפיק חיזויים. המערכת משווה כל תחזית לכל ערך של תווית. ההפרש בין התחזית לבין ערך התווית הוא ההפסד של הדוגמה הזו. המערכת מסכמת את ההפסדים של כל הדוגמאות כדי לחשב את ההפסד הכולל של האצווה הנוכחית.
2. במהלך המעבר לאחור (backpropagation), המערכת מצמצמת את אובדן המידע על ידי התאמת המשקלים של כל הנוירונים בכל השכבות הנסתרות.

נוירונים מלאכותיות מכילות בדרך כלל הרבה נוירונים בהרבה שכבות נסתרות. כל אחד מהנוירונים האלה תורם להפסד הכולל בדרכים שונות. האלגוריתם Backpropagation קובע אם להגדיל או להקטין את המשקלים שמוחלים על נוירונים מסוימים.

קצב הלמידה הוא מכפיל שקובע את מידת ההגדלה או ההקטנה של כל משקל בכל מעבר לאחור. שיעור למידה גבוה יגדיל או יקטין כל משקל יותר משיעור למידה נמוך.

במונחים של חשבון אינפיניטסימלי, backpropagation מיישם את כלל השרשרת מתוך חשבון אינפיניטסימלי. כלומר, בשיטת backpropagation מחושב הנגזרת החלקית של השגיאה ביחס לכל פרמטר.

לפני שנים, מומחים ל-ML היו צריכים לכתוב קוד כדי להטמיע backpropagation. ממשקי API מודרניים של למידת מכונה, כמו Keras, מטמיעים עכשיו בשבילכם את האלגוריתם backpropagation. סוף סוף!

מידע נוסף זמין במאמר רשתות עצביות בקורס המקוצר על למידת מכונה.

אצווה

#fundamentals

קבוצת הדוגמאות שמשמשת באיטרציה אחת של אימון. גודל האצווה קובע את מספר הדוגמאות באצווה.

בקטע epoch מוסבר איך קבוצת נתונים קשורה ל-epoch.

מידע נוסף זמין במאמר רגרסיה ליניארית: היפר-פרמטרים בקורס המקוצר על למידת מכונה.

גודל אצווה

#fundamentals

מספר הדוגמאות באצווה. לדוגמה, אם גודל האצווה הוא 100, המודל מעבד 100 דוגמאות לכל איטרציה.

אלה כמה אסטרטגיות פופולריות לגודל אצווה:

• ‫Stochastic Gradient Descent (SGD), שבו גודל האצווה הוא 1.
• קבוצת נתונים מלאה, שבה גודל הקבוצה הוא מספר הדוגמאות בקבוצת האימון כולה. לדוגמה, אם קבוצת האימון מכילה מיליון דוגמאות, גודל האצווה יהיה מיליון דוגמאות. שיטה של עדכון מלא של נתונים היא בדרך כלל לא יעילה.
• מיני-batch שבו גודל ה-batch הוא בדרך כלל בין 10 ל-1,000. בדרך כלל, אסטרטגיית המיני-batch היא היעילה ביותר.

מידע נוסף מפורט במאמרים הבאים:

• מערכות ML לייצור: הסקה סטטית לעומת הסקה דינמית בקורס המקוצר על למידת מכונה.
• מדריך לשיפור הביצועים של למידה עמוקה.

הטיה (אתיקה/הוגנות)

#responsible

#fundamentals

1. הצגת סטריאוטיפים, דעות קדומות או העדפה של דברים, אנשים או קבוצות מסוימים על פני אחרים. ההטיות האלה יכולות להשפיע על איסוף הנתונים ועל הפרשנות שלהם, על עיצוב המערכת ועל האופן שבו המשתמשים מבצעים אינטראקציה עם המערכת. דוגמאות להטיות מסוג זה:

• הטיית אוטומציה
• הטיית אישור
• הטיה של עורכי הניסוי
• הטיה בשיוך לקבוצה
• הטיה מרומזת
• הטיה לטובת קבוצת השייכות
• הטיה של הומוגניות בקבוצה החיצונית

2. שגיאה שיטתית שנובעת מהליך דגימה או דיווח. דוגמאות להטיות מסוג זה:

• הטיה בסיקור
• הטיית אי-תגובה
• הטיית השתתפות
• הטיית דיווח
• הטיית דגימה
• הטיית בחירה

לא להתבלבל עם מונח ההטיה במודלים של למידת מכונה או עם הטיה בתחזית.

מידע נוסף זמין במאמר הוגנות: סוגי הטיה בקורס המזורז ללימוד מכונת למידה.

הטיה (מתמטיקה) או מונח הטיה

#fundamentals

נקודת חיתוך או היסט מנקודת המוצא. הטיה היא פרמטר במודלים של למידת מכונה, שמסומל באחד מהערכים הבאים:

• b
• w₀

לדוגמה, הטיה היא b בנוסחה הבאה:

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

בקו דו-ממדי פשוט, הטיה פשוט מייצגת את נקודת החיתוך עם ציר ה-y. לדוגמה, ההטיה של הקו באיור הבא היא 2.

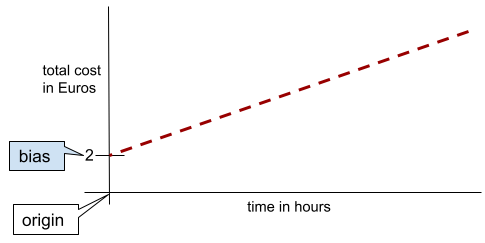
ההטיה קיימת כי לא כל המודלים מתחילים מהמקור (0,0). לדוגמה, נניח שעלות הכניסה לפארק שעשועים היא 2 אירו, ועל כל שעה שהלקוח נמצא בפארק הוא משלם עוד 0.5 אירו. לכן, למודל שממפה את העלות הכוללת יש הטיה של 2 כי העלות הנמוכה ביותר היא 2 אירו.

הטיה לא זהה להטיה באתיקה ובהוגנות או להטיה בתחזיות.

מידע נוסף זמין במאמר רגרסיה ליניארית בקורס המקוצר על למידת מכונה.

סיווג בינארי

#fundamentals

סוג של משימת סיווג שבה המודל חוזה אחת משתי קטגוריות שאינן חופפות:

• הסיווג החיובי
• ה-negative class

לדוגמה, כל אחד משני המודלים הבאים של למידת מכונה מבצע סיווג בינארי:

• מודל שקובע אם הודעות אימייל הן ספאם (הסיווג החיובי) או לא ספאם (הסיווג השלילי).
• מודל שמעריך תסמינים רפואיים כדי לקבוע אם לאדם מסוים יש מחלה מסוימת (הסיווג החיובי) או שאין לו את המחלה הזו (הסיווג השלילי).

ההפך מסיווג רב-מחלקתי.

אפשר לעיין גם במאמרים בנושא רגרסיה לוגיסטית וסף סיווג.

מידע נוסף זמין במאמר סיווג בקורס המקוצר על למידת מכונה.

bucketing

#fundamentals

המרת תכונה אחת לכמה תכונות בינאריות שנקראות buckets או bins, בדרך כלל על סמך טווח ערכים. התכונה שנחתכת היא בדרך כלל תכונה רציפה.

לדוגמה, במקום לייצג טמפרטורה כמאפיין רציף של נקודה צפה, אפשר לחלק טווחי טמפרטורות לקטגוריות נפרדות, כמו:

• ‫<= 10 degrees Celsius would be the "cold" bucket.
• ‫11 עד 24 מעלות צלזיוס יהיו בקטגוריה 'ממוזג'.
• ‫>= 25 degrees Celsius יהיה הדלי 'warm'.

המודל יתייחס לכל הערכים באותו דלי באופן זהה. לדוגמה, הערכים 13 ו-22 נמצאים שניהם בדלי של אזורים ממוזגים, ולכן המודל מתייחס לשני הערכים בצורה זהה.

כדי לראות הערות נוספות, לוחצים על הסמל.

אם מייצגים את הטמפרטורה כמאפיין רציף, המודל מתייחס לטמפרטורה כמאפיין יחיד. אם מייצגים את הטמפרטורה באמצעות שלוש קטגוריות, המודל מתייחס לכל קטגוריה כאל תכונה נפרדת. כלומר, מודל יכול ללמוד קשרים נפרדים של כל קטגוריה לתווית. לדוגמה, מודל של רגרסיה לינארית יכול ללמוד משקלים נפרדים לכל קבוצת משנה.

הגדלת מספר הדליים מסבכת את המודל, כי היא מגדילה את מספר הקשרים שהמודל צריך ללמוד. לדוגמה, קטגוריות קרות, ממוזגות וחמות הן למעשה שלוש תכונות נפרדות לאימון המודל. אם תחליטו להוסיף עוד שני מאגרי נתונים – למשל, מאגר נתונים של נתונים קפואים ומאגר נתונים של נתונים פעילים – המודל יצטרך להתאמן על חמישה מאפיינים נפרדים.

איך יודעים כמה קטגוריות ליצור, או מה צריך להיות טווח הערכים של כל קטגוריה? בדרך כלל צריך לבצע לא מעט ניסויים כדי לקבל תשובות.

---

מידע נוסף מופיע במאמר נתונים מספריים: חלוקה לקטגוריות בקורס המקוצר על למידת מכונה.

C

נתונים קטגוריים

#fundamentals

מאפיינים עם קבוצה ספציפית של ערכים אפשריים. לדוגמה, נניח שיש מאפיין קטגוריאלי בשם traffic-light-state, שיכול לקבל רק אחד משלושת הערכים האפשריים הבאים:

• red
• yellow
• green

אם מייצגים את traffic-light-state כמאפיין קטגוריאלי, מודל יכול ללמוד את ההשפעות השונות של red, green ו-yellow על התנהגות הנהג.

תכונות קטגוריות נקראות לפעמים תכונות בדידות.

ההפך מנתונים מספריים.

מידע נוסף זמין במאמר עבודה עם נתונים שמחולקים לקטגוריות בקורס המקוצר על למידת מכונה.

כיתה

#fundamentals

קטגוריה שתווית יכולה להשתייך אליה. לדוגמה:

• במודל סיווג בינארי שמזהה ספאם, שתי המחלקות יכולות להיות ספאם ולא ספאם.
• במודל סיווג רב-מחלקתי שמזהה גזעי כלבים, המחלקות יכולות להיות פודל, ביגל, פאג וכו'.

מודל סיווג חוזה את הסיווג. לעומת זאת, מודל רגרסיה חוזה מספר ולא סיווג.

מידע נוסף זמין במאמר סיווג בקורס המקוצר על למידת מכונה.

מודל סיווג

#fundamentals

מודל שהחיזוי שלו הוא סיווג. לדוגמה, כל אלה הם מודלים של סיווג:

• מודל שמנבא את השפה של משפט קלט (צרפתית? ספרדית? איטלקית?).
• מודל שמנבא מיני עצים (אדר? אלון? באובב?).
• מודל שמנבא את הסיווג החיובי או השלילי של מצב רפואי מסוים.

לעומת זאת, מודלים של רגרסיה חוזים מספרים ולא סיווגים.

שני סוגים נפוצים של מודלים לסיווג הם:

• סיווג בינארי
• סיווג רב-מחלקתי

סף סיווג (classification threshold)

#fundamentals

בסיווג בינארי, מספר בין 0 ל-1 שממיר את הפלט הגולמי של מודל רגרסיה לוגיסטית לתחזית של הסיווג החיובי או של הסיווג השלילי. חשוב לזכור שסף הסיווג הוא ערך שנבחר על ידי בן אדם, ולא ערך שנבחר על ידי אימון המודל.

מודל רגרסיה לוגיסטית מחזיר ערך גולמי בין 0 ל-1. לאחר מכן:

• אם הערך הגולמי הזה גדול יותר מסף הסיווג, אז המערכת חוזה את הסיווג החיובי.
• אם הערך הגולמי הזה נמוך מסף הסיווג, המערכת תנבא את הסיווג השלילי.

לדוגמה, נניח שסף הסיווג הוא 0.8. אם הערך הגולמי הוא 0.9, המודל חוזה את הסיווג החיובי. אם הערך הגולמי הוא 0.7, המודל חוזה את המחלקה השלילית.

בחירת סף הסיווג משפיעה מאוד על מספר התוצאות החיוביות הכוזבות והתוצאות השליליות הכוזבות.

כדי לראות הערות נוספות, לוחצים על הסמל.

כשהמודלים או מערכי הנתונים מתפתחים, לפעמים מהנדסים משנים גם את ערך הסף של הסיווג. כשסף הסיווג משתנה, חיזויים חיוביים של מחלקה יכולים להפוך פתאום למחלקות שליליות, ולהיפך.

לדוגמה, נניח שיש מודל בינארי לסיווג של חיזוי מחלות. נניח שבשנה הראשונה שבה המערכת פועלת:

• הערך הגולמי של מטופל מסוים הוא 0.95.
• סף הסיווג הוא 0.94.

לכן המערכת מאבחנת את המחלקה החיובית. (המטופל נאנח, "אוי לא! I'm sick!")

שנה לאחר מכן, יכול להיות שהערכים ייראו כך:

• הערך הגולמי של אותו מטופל נשאר 0.95.
• סף הסיווג משתנה ל-0.97.

לכן, המערכת מסווגת מחדש את המטופל הזה כסיווג השלילי. ("יום שמח! I'm not sick.") אותו מטופל. אבחון שונה.

---

מידע נוסף זמין במאמר ערכי סף ומטריצת בלבול בקורס המקוצר על למידת מכונה.

מסווג

#fundamentals

מונח לא רשמי למודל סיווג.

קבוצת נתונים לא מאוזנת מבחינת כיתות

#fundamentals

מערך נתונים של סיווג שבו המספר הכולל של תוויות של כל סיווג שונה באופן משמעותי. לדוגמה, נניח שיש קבוצת נתונים של סיווג בינארי עם שתי תוויות שמחולקות באופן הבא:

• ‫1,000,000 תוויות שליליות
• ‫10 תוויות חיוביות

היחס בין תוויות שליליות לחיוביות הוא 100,000 ל-1, ולכן זהו מערך נתונים עם חוסר איזון בין המחלקות.

לעומת זאת, מערך הנתונים הבא הוא מאוזן לפי מחלקות כי היחס בין התוויות השליליות לתוויות החיוביות קרוב יחסית ל-1:

• ‫517 תוויות שליליות
• ‫483 תוויות חיוביות

יכול להיות גם חוסר איזון בין המחלקות במערכי נתונים עם כמה מחלקות. לדוגמה, מערך הנתונים הבא של סיווג רב-מחלקתי הוא גם לא מאוזן מבחינת מחלקות, כי לתווית אחת יש הרבה יותר דוגמאות מאשר לשתי התוויות האחרות:

• ‫1,000,000 תוויות עם הסיווג 'ירוק'
• ‫200 תוויות עם המחלקה 'סגול'
• ‫350 תוויות עם המחלקה orange

אימון של מערכי נתונים לא מאוזנים בכיתות יכול להציב אתגרים מיוחדים. פרטים נוספים זמינים במאמר Imbalanced datasets (מערכי נתונים לא מאוזנים) בקורס Machine Learning Crash Course (קורס מקוצר על למידת מכונה).

אפשר לעיין גם בערכים אנטרופיה, מחלקת הרוב ומחלקת המיעוט.

חיתוך

#fundamentals

טכניקה לטיפול בערכים חריגים באמצעות אחת מהפעולות הבאות או שתיהן:

• הפחתת ערכי מאפיינים שגדולים מסף מקסימלי מסוים עד לסף המקסימלי הזה.
• הגדלת ערכי התכונות שקטנים מסף מינימלי עד לסף המינימלי הזה.

לדוגמה, נניח שפחות מ-0.5% מהערכים של תכונה מסוימת נמצאים מחוץ לטווח 40-60. במקרה כזה, אפשר לבצע את הפעולות הבאות:

• כל הערכים מעל 60 (הסף המקסימלי) יקוצצו ל-60 בדיוק.
• כל הערכים שקטנים מ-40 (סף המינימום) יוגבלו ל-40 בדיוק.

ערכים חריגים עלולים לפגוע במודלים, ולפעמים לגרום למשקלים לגלוש במהלך האימון. חלק מהערכים החריגים יכולים גם לפגוע באופן משמעותי במדדים כמו דיוק. חיתוך הוא טכניקה נפוצה להגבלת הנזק.

חיתוך גרדיאנטים מאלץ ערכי גרדיאנט בטווח מוגדר במהלך האימון.

מידע נוסף זמין במאמר נתונים מספריים: נורמליזציה בסדנה ללימוד מכונת למידה.

מטריצת בלבול

#fundamentals

טבלה בגודל NxN שמסכמת את מספר התחזיות הנכונות והלא נכונות שמודל סיווג יצר. לדוגמה, הנה מטריצת בלבול עבור מודל של סיווג בינארי:

	גידול (צפוי)	Non-Tumor (predicted)
גידול (ערך סף)	‫18 (TP)	‫1 (FN)
Non-Tumor (ground truth)	‫6 (FP)	‫452 (TN)

מטריצת הבלבול שלמעלה מציגה את הנתונים הבאים:

• מתוך 19 התחזיות שבהן האמת הבסיסית הייתה Tumor, המודל סיווג 18 מהן בצורה נכונה ו-1 בצורה שגויה.
• מתוך 458 התחזיות שבהן האמת הבסיסית הייתה Non-Tumor, המודל סיווג 452 בצורה נכונה ו-6 בצורה שגויה.

מטריצת הבלבול של בעיית סיווג רב-מחלקתי יכולה לעזור לכם לזהות דפוסים של טעויות. לדוגמה, נניח שיש לנו מטריצת בלבול למודל סיווג רב-סוגי עם 3 סוגים, שמסווג 3 סוגים שונים של אירוסים (Virginica, ‏ Versicolor ו-Setosa). כשנתוני האמת היו Virginica, מטריצת השגיאות מראה שהמודל היה הרבה יותר סביר לטעות ולחזות Versicolor מאשר Setosa:

	Setosa (predicted)	Versicolor (צפוי)	Virginica (predicted)
Setosa (ערך סף)	88	12	0
Versicolor (ערכי סף)	6	141	7
Virginica (ערכי סף)	2	27	109

דוגמה נוספת: מטריצת בלבול יכולה לחשוף שמודל שאומן לזיהוי ספרות בכתב יד נוטה לחזות בטעות 9 במקום 4, או לחזות בטעות 1 במקום 7.

מטריצות השגיאה מכילות מספיק מידע כדי לחשב מגוון מדדי ביצועים, כולל דיוק ורגישות.

תכונה רציפה

#fundamentals

תכונה של נקודה צפה עם טווח אינסופי של ערכים אפשריים, כמו טמפרטורה או משקל.

ההבדל בין התכונה הזו לבין תכונה נפרדת.

התכנסות

#fundamentals

מצב שמתקבל כשערכי ההפסד משתנים מעט מאוד או לא משתנים בכלל בכל איטרציה. לדוגמה, מעקומת ההפסד הבאה אפשר לראות שההתכנסות מתרחשת בערך אחרי 700 איטרציות:

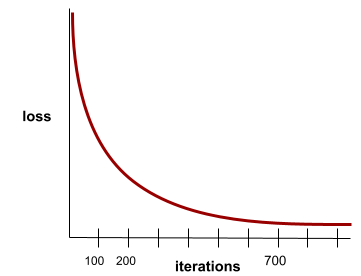
מודל מתכנס כשאימון נוסף לא ישפר אותו.

בלמידה עמוקה, ערכי ההפסד נשארים לפעמים קבועים או כמעט קבועים במשך הרבה איטרציות לפני שהם יורדים בסופו של דבר. במהלך תקופה ארוכה של ערכי הפסד קבועים, יכול להיות שתקבלו באופן זמני תחושה מוטעית של התכנסות.

אפשר לעיין גם במאמר בנושא עצירה מוקדמת.

מידע נוסף זמין במאמר בנושא התכנסות מודלים ועקומות הפסד בקורס המקוצר על למידת מכונה.

D

DataFrame

#fundamentals

סוג נתונים פופולרי של pandas לייצוג מערכי נתונים בזיכרון.

אובייקט DataFrame דומה לטבלה או לגיליון אלקטרוני. לכל עמודה ב-DataFrame יש שם (כותרת), ולכל שורה יש מספר ייחודי.

כל עמודה ב-DataFrame בנויה כמו מערך דו-ממדי, אבל לכל עמודה אפשר להקצות סוג נתונים משלה.

אפשר לעיין גם בדף העיון הרשמי של pandas.DataFrame.

קבוצת נתונים

#fundamentals

אוסף של נתונים גולמיים, בדרך כלל (אבל לא רק) באחד מהפורמטים הבאים:

• גיליון אלקטרוני
• קובץ בפורמט CSV (ערכים מופרדים בפסיקים)

מודל עמוק

#fundamentals

רשת עצבית שמכילה יותר משכבה נסתרת.

מודל עמוק נקרא גם רשת נוירונים עמוקה.

ההבדל בינו לבין מודל רחב.

תכונה צפופה

#fundamentals

תכונה שרוב הערכים שלה או כולם הם לא אפס, בדרך כלל טנזור של ערכים מסוג נקודה צפה. לדוגמה, טנסור 10-אלמנטים הבא הוא צפוף כי 9 מהערכים שלו הם לא אפס:

8

3

7

5

2

4

0

4

9

6

ההבדל בין התכונה הזו לבין sparse feature.

עומק

#fundamentals

הסכום של הרכיבים הבאים ברשת נוירונים:

• מספר השכבות הנסתרות
• מספר שכבות הפלט, שבדרך כלל הוא 1
• מספר שכבות ההטמעה

לדוגמה, רשת עצבית עם חמש שכבות נסתרות ושכבת פלט אחת היא בעומק 6.

שימו לב ששכבת הקלט לא משפיעה על העומק.

תכונה נפרדת

#fundamentals

תכונה עם קבוצה סופית של ערכים אפשריים. לדוגמה, מאפיין שהערכים שלו יכולים להיות רק animal (בעל חיים), vegetable (ירק) או mineral (מינרל) הוא מאפיין נפרד (או קטגורי).

ההפך מתכונה מתמשכת.

דינמי

#fundamentals

משהו שעושים לעיתים קרובות או באופן רציף. המונחים דינמי ואונליין הם מילים נרדפות בתחום למידת המכונה. אלה שימושים נפוצים במונחים דינמי ואונליין בלמידת מכונה:

• מודל דינמי (או מודל אונליין) הוא מודל שעובר אימון מחדש לעיתים קרובות או באופן רציף.
• הדרכה דינמית (או הדרכה אונליין) היא תהליך של הדרכה בתדירות גבוהה או באופן רציף.
• הסקת מסקנות דינמית (או הסקת מסקנות אונליין) היא תהליך של יצירת תחזיות לפי דרישה.

מודל דינמי

#fundamentals

מודל שעובר אימון מחדש לעיתים קרובות (אולי אפילו באופן רציף). מודל דינמי הוא 'לומד לכל החיים' שמתאים את עצמו כל הזמן לנתונים משתנים. מודל דינמי נקרא גם מודל אונליין.

השוואה למודל סטטי.

E

עצירה מוקדמת

#fundamentals

שיטה לרגולריזציה שכוללת סיום של אימון לפני שההפסד של האימון מפסיק לרדת. בשיטת העצירה המוקדמת, עוצרים בכוונה את אימון המודל כשההפסד במערך נתוני האימות מתחיל לעלות, כלומר כשביצועי ההכללה מתדרדרים.

כדי לראות הערות נוספות, לוחצים על הסמל.

יכול להיות שההפסקה המוקדמת תיראה לכם לא הגיונית. אחרי הכול, אם אומרים למודל להפסיק את האימון בזמן שההפסד עדיין יורד, זה כמו להגיד לשף להפסיק לבשל לפני שהקינוח נאפה לגמרי. עם זאת, אימון מודל למשך זמן ארוך מדי עלול להוביל להתאמת יתר. כלומר, אם מאמנים מודל יותר מדי זמן, יכול להיות שהמודל יתאים לנתוני האימון בצורה כל כך מדויקת שהוא לא יבצע חיזויים טובים לגבי דוגמאות חדשות.

---

ההפך מיציאה מוקדמת.

שכבת הטמעה

#fundamentals

שכבה נסתרת מיוחדת שעוברת אימון על מאפיין קטגורי עם הרבה ממדים, כדי ללמוד בהדרגה וקטור הטמעה עם פחות ממדים. שכבת הטמעה מאפשרת לרשת נוירונים להתאמן ביעילות רבה יותר מאשר אימון רק על תכונת סיווג רב-ממדית.

לדוגמה, נכון לעכשיו, Earth תומך בכ-73,000 מיני עצים. נניח שהתכונה במודל היא מיני עצים, ולכן שכבת הקלט של המודל כוללת וקטור one-hot באורך 73,000 אלמנטים. לדוגמה, יכול להיות שהתו baobab ייוצג כך:

מערך עם 73,000 רכיבים הוא ארוך מאוד. אם לא מוסיפים למודל שכבת הטמעה, האימון ייקח הרבה זמן כי צריך להכפיל 72,999 אפסים. יכול להיות שתבחרו ששכבת ההטמעה תכלול 12 מימדים. כתוצאה מכך, שכבת ההטמעה תלמד בהדרגה וקטור הטמעה חדש לכל מין של עץ.

במצבים מסוימים, גיבוב הוא חלופה סבירה לשכבת הטמעה.

מידע נוסף זמין במאמר Embeddings בקורס המקוצר על למידת מכונה.

תקופה של זמן מערכת

#fundamentals

מעבר אימון מלא על כל מערך האימון כך שכל דוגמה עברה עיבוד פעם אחת.

אפוקה מייצגת N/גודל אצווה אימונים של איטרציות, כאשר N הוא מספר הדוגמאות הכולל.

לדוגמה, נניח את הדברים הבאים:

• מערך הנתונים מורכב מ-1,000 דוגמאות.
• גודל הקבוצה הוא 50 דוגמאות.

לכן, כל אפוקה דורשת 20 איטרציות:

1 epoch = (N/batch size) = (1,000 / 50) = 20 iterations

מידע נוסף זמין במאמר רגרסיה ליניארית: היפר-פרמטרים בקורס המקוצר על למידת מכונה.

דוגמה

#fundamentals

הערכים של שורה אחת ב-features ואולי גם label. דוגמאות בלמידה מונחית מתחלקות לשתי קטגוריות כלליות:

• דוגמה עם תווית מורכבת מתכונה אחת או יותר ומתווית. דוגמאות עם תוויות משמשות במהלך האימון.
• דוגמה לא מסומנת מורכבת מתכונה אחת או יותר, אבל לא כוללת תווית. דוגמאות ללא תוויות משמשות במהלך ההסקה.

לדוגמה, נניח שאתם מאמנים מודל כדי לקבוע את ההשפעה של תנאי מזג האוויר על ציוני התלמידים במבחנים. הנה שלוש דוגמאות עם תוויות:

תכונות			תווית
טמפרטורה	לחות	לחץ	ציון הבדיקה
15	47	998	טוב
19	34	1020	מצוינת
18	92	1012	גרועה

הנה שלוש דוגמאות ללא תווית:

טמפרטורה	לחות	לחץ
12	62	1014
21	47	1017
19	41	1021

השורה במערך נתונים היא בדרך כלל המקור הגולמי לדוגמה. כלומר, דוגמה בדרך כלל מורכבת מקבוצת משנה של העמודות במערך הנתונים. בנוסף, התכונות בדוגמה יכולות לכלול גם תכונות סינתטיות, כמו תכונות מצטלבות.

מידע נוסף זמין במאמר למידה מפוקחת בקורס מבוא ללמידת מכונה.

F

תוצאה שלילית שגויה (FN)

#fundamentals

#Metric

דוגמה שבה המודל מנבא בטעות את הסיווג השלילי. לדוגמה, המודל מנבא שהודעת אימייל מסוימת אינה ספאם (הסיווג השלילי), אבל הודעת האימייל הזו היא למעשה ספאם.

תוצאה חיובית שגויה (FP)

#fundamentals

#Metric

דוגמה שבה המודל חוזה בטעות את הסיווג החיובי. לדוגמה, המודל חוזה שהודעת אימייל מסוימת היא ספאם (הסיווג החיובי), אבל הודעת האימייל הזו לא ספאם בפועל.

מידע נוסף זמין במאמר ערכי סף ומטריצת בלבול בקורס המקוצר על למידת מכונה.

שיעור התוצאות החיוביות השגויות (FPR)

#fundamentals

#Metric

השיעור של הדוגמאות השליליות בפועל שהמודל טעה בהן וחיזה את הסיווג החיובי. הנוסחה הבאה משמשת לחישוב שיעור התוצאות החיוביות השגויות:

$$\text{false positive rate} = \frac{\text{false positives}}{\text{false positives} + \text{true negatives}}$$

שיעור התוצאות החיוביות השגויות הוא ציר ה-x בעקומת ROC.

מידע נוסף זמין במאמר בנושא סיווג: ROC ו-AUC בקורס המקוצר על למידת מכונה.

מאפיין

#fundamentals

משתנה קלט למודל למידת מכונה. דוגמה מורכבת מתכונה אחת או יותר. לדוגמה, נניח שאתם מאמנים מודל כדי לקבוע את ההשפעה של תנאי מזג האוויר על ציוני התלמידים במבחנים. בטבלה הבאה מוצגות שלוש דוגמאות, שכל אחת מהן מכילה שלוש תכונות ותווית אחת:

תכונות			תווית
טמפרטורה	לחות	לחץ	ציון הבדיקה
15	47	998	92
19	34	1020	84
18	92	1012	87

ניגודיות עם תווית.

מידע נוסף זמין במאמר Supervised Learning (למידה מפוקחת) בקורס Introduction to Machine Learning (מבוא ללמידת מכונה).

שילוב מאפיינים

#fundamentals

תכונה סינתטית שנוצרת על ידי 'הצלבה' של תכונות קטגוריות או תכונות שמוגדרות כקבוצות.

לדוגמה, נניח שיש מודל של 'חיזוי מצב רוח' שמייצג טמפרטורה באחת מארבע הקטגוריות הבאות:

• freezing
• chilly
• temperate
• warm

המשתנה הזה מייצג את מהירות הרוח באחד משלושת הסיווגים הבאים:

• still
• light
• windy

בלי תכונות משולבות, המודל הלינארי מתאמן באופן עצמאי על כל אחד משבעת הדליים הקודמים. לכן, המודל מתאמן על, למשל, freezing בנפרד מהאימון על, למשל, windy.

אפשרות אחרת היא ליצור שילוב של טמפרטורה ומהירות רוח. לתכונה הסינתטית הזו יהיו 12 ערכים אפשריים:

• freezing-still
• freezing-light
• freezing-windy
• chilly-still
• chilly-light
• chilly-windy
• temperate-still
• temperate-light
• temperate-windy
• warm-still
• warm-light
• warm-windy

הודות לשילובים של תכונות, המודל יכול ללמוד את ההבדלים במצב הרוח בין יום freezing-windy ליום freezing-still.

אם תיצרו תכונה סינתטית משתי תכונות שלכל אחת מהן יש הרבה דליים שונים, לתכונה המשולבת שתתקבל יהיה מספר עצום של שילובים אפשריים. לדוגמה, אם לתכונה אחת יש 1,000 קטגוריות ולתכונה השנייה יש 2,000 קטגוריות, לתכונה המשולבת שמתקבלת יש 2,000,000 קטגוריות.

באופן רשמי, הצלבה היא מכפלה קרטזית.

השימוש בתכונות משולבות נעשה בעיקר עם מודלים לינאריים, ובדרך כלל לא עם רשתות עצביות.

מידע נוסף זמין במאמר נתונים קטגוריים: שילובים של תכונות בקורס המקוצר על למידת מכונה.

הנדסת פיצ'רים (feature engineering)

#fundamentals

#TensorFlow

תהליך שכולל את השלבים הבאים:

1. קביעה של תכונות שעשויות להיות שימושיות באימון מודל.
2. המרת נתונים גולמיים ממערך הנתונים לגרסאות יעילות של התכונות האלה.

לדוגמה, יכול להיות שתקבעו ש-temperature הוא תכונה שימושית. אחר כך אפשר להתנסות בחלוקה לקטגוריות כדי לשפר את היכולת של המודל ללמוד מטווחים שונים של temperature.

הנדסת תכונות נקראת לפעמים חילוץ תכונות או יצירת תכונות.

כדי לראות הערות נוספות על TensorFlow, לוחצים על הסמל.

ב-TensorFlow, הנדסת תכונות לרוב מתייחסת להמרה של רשומות גולמיות בקובץ יומן למאגרי פרוטוקולים של tf.Example. מידע נוסף זמין במאמר בנושא tf.Transform.

---

מידע נוסף זמין במאמר נתונים מספריים: איך מודל מעכל נתונים באמצעות וקטורים של תכונות בסדנה המקוונת בנושא למידת מכונה.

מערך תכונות

#fundamentals

קבוצת התכונות שעליהן מתבסס האימון של המודל של למידת המכונה. לדוגמה, קבוצת תכונות פשוטה למודל שמנבא מחירי דיור יכולה לכלול מיקוד, גודל הנכס ומצב הנכס.

וקטור מאפיינים

#fundamentals

מערך של ערכי feature שמרכיבים example. וקטור המאפיינים משמש כקלט במהלך האימון ובמהלך ההסקה. לדוגמה, וקטור התכונות של מודל עם שתי תכונות נפרדות יכול להיות:

[0.92, 0.56]

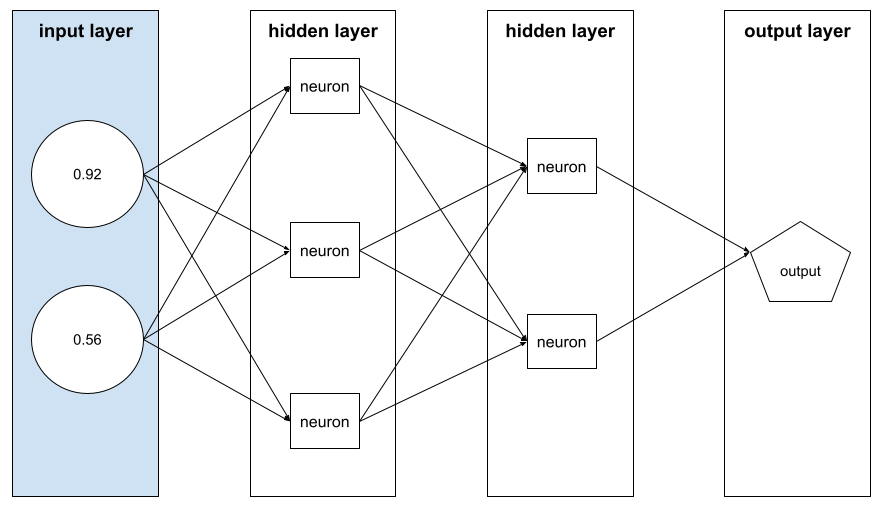
בכל דוגמה מופיעים ערכים שונים של וקטור התכונות, ולכן וקטור התכונות של הדוגמה הבאה יכול להיות משהו כזה:

[0.73, 0.49]

הנדסת תכונות קובעת איך לייצג תכונות בווקטור התכונות. לדוגמה, מאפיין קטגורי בינארי עם חמישה ערכים אפשריים יכול להיות מיוצג באמצעות קידוד one-hot. במקרה כזה, החלק של וקטור התכונות בדוגמה מסוימת יכלול ארבעה אפסים ו-1.0 אחד במיקום השלישי, באופן הבא:

[0.0, 0.0, 1.0, 0.0, 0.0]

דוגמה נוספת: נניח שהמודל שלכם מורכב משלושה מאפיינים:

• תכונה קטגורית בינארית עם חמישה ערכים אפשריים שמיוצגים באמצעות קידוד one-hot. לדוגמה: [0.0, 1.0, 0.0, 0.0, 0.0]
• תכונה קטגורית בינארית נוספת עם שלושה ערכים אפשריים שמיוצגים באמצעות קידוד one-hot. לדוגמה: [0.0, 0.0, 1.0]
• תכונה מסוג נקודה צפה, לדוגמה: 8.3.

במקרה כזה, וקטור התכונות של כל דוגמה ייוצג על ידי תשעה ערכים. בהינתן הערכים לדוגמה ברשימה הקודמת, וקטור התכונות יהיה:

0.0
1.0
0.0
0.0
0.0
0.0
0.0
1.0
8.3

מידע נוסף זמין במאמר נתונים מספריים: איך מודל מעכל נתונים באמצעות וקטורים של תכונות בסדנה המקוונת בנושא למידת מכונה.

לולאת משוב

#fundamentals

במערכות ללמידת מכונה, מצב שבו החיזויים של מודל מסוים משפיעים על נתוני האימון של אותו מודל או של מודל אחר. לדוגמה, מודל שממליץ על סרטים ישפיע על הסרטים שאנשים רואים, מה שישפיע על מודלים עתידיים להמלצות על סרטים.

מידע נוסף זמין במאמר מערכות ML לייצור: שאלות שכדאי לשאול בסדנה ללימוד למידת מכונה.

G

הכללה

#fundamentals

היכולת של מודל לבצע חיזויים נכונים לגבי נתונים חדשים שלא נראו קודם. מודל שיכול להכליל הוא ההפך ממודל שמותאם יתר על המידה.

כדי לראות הערות נוספות, לוחצים על הסמל.

מאמנים מודל על הדוגמאות שבקבוצת האימון. כתוצאה מכך, המודל לומד את המאפיינים הייחודיים של הנתונים במערך האימון. הכללה (Generalization) בודקת בעצם אם המודל יכול ליצור תחזיות טובות לגבי דוגמאות שלא נכללות במערך האימון.

כדי לעודד הכללה, רגולריזציה עוזרת למודל להתאמן בצורה פחות מדויקת למאפיינים הייחודיים של הנתונים במערך האימון.

---

מידע נוסף מופיע במאמר הכללה בקורס המקוצר על למידת מכונה.

עקומת הכללה

#fundamentals

תרשים של הפסד האימון ושל הפסד האימות כפונקציה של מספר האיטרציות.

עקומת הכללה יכולה לעזור לכם לזהות התאמת יתר אפשרית. לדוגמה, עקומת ההכללה הבאה מצביעה על התאמת יתר, כי הפסד האימות בסופו של דבר גבוה משמעותית מהפסד האימון.

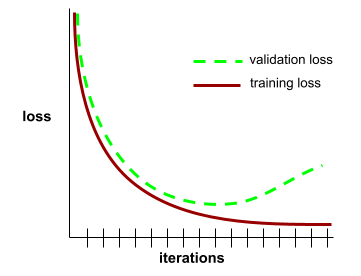
מידע נוסף מופיע במאמר הכללה בקורס המקוצר על למידת מכונה.

ירידת גרדיאנט

#fundamentals

טכניקה מתמטית שמטרתה למזער את ההפסד. האלגוריתם Gradient descent (ירידת גרדיאנט) משנה באופן איטרטיבי את המשקלים ואת ההטיות, ומוצא בהדרגה את השילוב הטוב ביותר לצמצום ההפסד.

השיטה של ירידת גרדיאנט קיימת כבר הרבה מאוד זמן, הרבה יותר זמן מלמידת מכונה.

מידע נוסף זמין במאמר רגרסיה לינארית: ירידה הדרגתית בסדנה ללימוד מכונת למידה.

ערכי סף (ground truth)

#fundamentals

ריאליטי.

מה שקרה בפועל.

לדוגמה, נניח שיש מודל של סיווג בינארי שמנבא אם סטודנט בשנה הראשונה באוניברסיטה יסיים את התואר תוך שש שנים. האמת הבסיסית של המודל הזה היא אם התלמיד או התלמידה סיימו את הלימודים תוך שש שנים או לא.

כדי לראות הערות נוספות, לוחצים על הסמל.

אנחנו מעריכים את איכות המודל בהשוואה לאמת הבסיסית. עם זאת, נתוני האמת לא תמיד מדויקים לחלוטין. לדוגמה, הנה כמה דוגמאות לפגמים פוטנציאליים בנתוני האמת:

• בדוגמה של סיום הלימודים, האם אנחנו בטוחים שרשומות סיום הלימודים של כל תלמיד תמיד נכונות? האם רישום הנתונים באוניברסיטה מתבצע בצורה מושלמת?
• נניח שהתווית היא ערך נקודה צפה שנמדד על ידי מכשירים (לדוגמה, ברומטרים). איך אפשר לוודא שכל המכשירים מכוילים באופן זהה או שכל קריאה בוצעה באותם תנאים?
• אם התווית היא עניין של דעה אנושית, איך אפשר לוודא שכל בודק אנושי מעריך את האירועים באותו אופן? כדי לשפר את העקביות, לפעמים מתערבים מומחים אנושיים.

---

H

שכבה נסתרת

#fundamentals

שכבה ברשת עצבית בין שכבת הקלט (התכונות) לבין שכבת הפלט (התחזית). כל שכבה מוסתרת מורכבת מנוירון אחד או יותר. לדוגמה, רשת הנוירונים הבאה מכילה שתי שכבות נסתרות, הראשונה עם שלושה נוירונים והשנייה עם שני נוירונים:

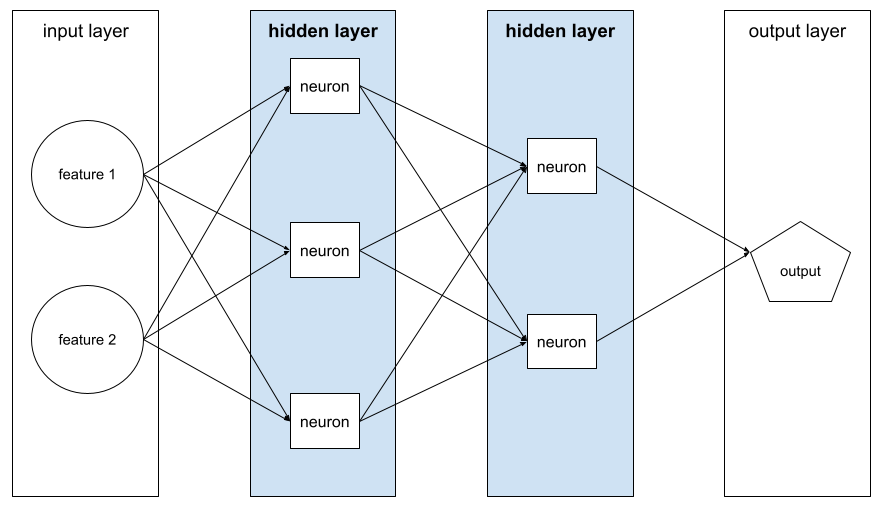
רשת עצבית עמוקה מכילה יותר משכבה נסתרת אחת. לדוגמה, האיור הקודם הוא רשת עצבית עמוקה כי המודל מכיל שתי שכבות מוסתרות.

מידע נוסף זמין במאמר רשתות עצביות: צמתים ושכבות מוסתרות בסדנה ללמידת מכונה.

היפר-פרמטר

#fundamentals

המשתנים שאתם או שירות לכוונון היפר-פרמטרים משנים במהלך הרצות עוקבות של אימון מודל. לדוגמה, קצב הלמידה הוא היפר-פרמטר. אפשר להגדיר את קצב הלמידה ל-0.01 לפני סשן אימון. אם תגיעו למסקנה ש-0.01 הוא ערך גבוה מדי, תוכלו להגדיר את קצב הלמידה ל-0.003 בסשן האימון הבא.

לעומת זאת, פרמטרים הם משקלים והטיות שונים שהמודל לומד במהלך האימון.

מידע נוסף זמין במאמר רגרסיה ליניארית: היפר-פרמטרים בקורס המקוצר על למידת מכונה.

I

בלתי תלויים ומחולקים באופן זהה (i.i.d)

#fundamentals

נתונים שנלקחים מהתפלגות שלא משתנה, וכל ערך שנלקח לא תלוי בערכים שנלקחו קודם. התפלגות i.i.d. היא הגז האידיאלי של למידת מכונה – מבנה מתמטי שימושי אבל כמעט אף פעם לא נמצא בדיוק בעולם האמיתי. לדוגמה, התפלגות המבקרים בדף אינטרנט עשויה להיות i.i.d. במהלך חלון זמן קצר. כלומר, ההתפלגות לא משתנה במהלך חלון הזמן הקצר הזה, והביקור של אדם אחד בדרך כלל לא תלוי בביקור של אדם אחר. עם זאת, אם תרחיבו את חלון הזמן הזה, יכול להיות שתראו הבדלים עונתיים במספר המבקרים בדף האינטרנט.

מידע נוסף מופיע במאמר בנושא nonstationarity.

היקש

#fundamentals

#generativeAI

בלמידת מכונה מסורתית, התהליך של ביצוע חיזויים על ידי החלת מודל שעבר אימון על דוגמאות לא מסומנות. מידע נוסף זמין במאמר בנושא למידה מפוקחת בקורס 'מבוא ל-ML'.

במודלים גדולים של שפה, הסקה היא התהליך של שימוש במודל מאומן כדי ליצור תשובה לקלט הנחיה.

למונח 'היסק' יש משמעות שונה בסטטיסטיקה. פרטים נוספים זמינים במאמר בוויקיפדיה בנושא הסקה סטטיסטית.

שכבת קלט

#fundamentals

השכבה של רשת הנוירונים שמכילה את וקטור התכונות. כלומר, שכבת הקלט מספקת דוגמאות לאימון או להסקת מסקנות. לדוגמה, שכבת הקלט ברשת העצבית הבאה מורכבת משני מאפיינים:

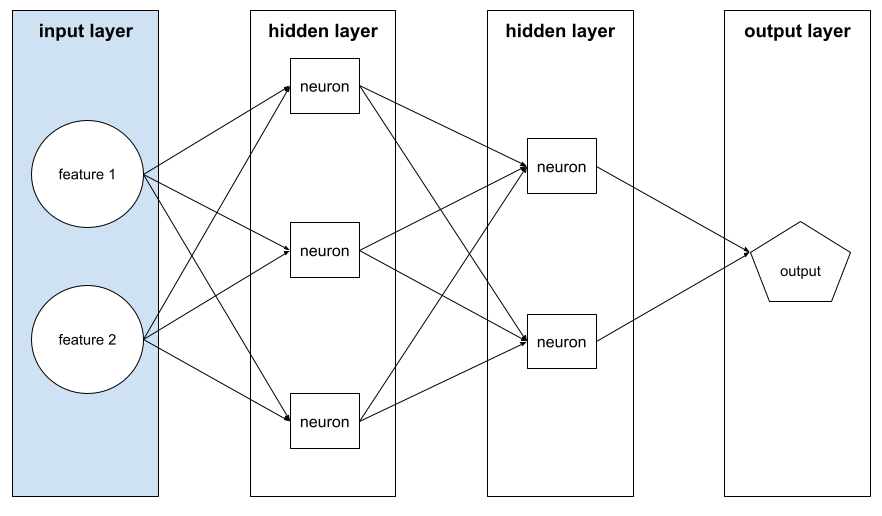
יכולת פירוש

#fundamentals

היכולת להסביר או להציג את הנימוקים של מודל למידת מכונה במונחים מובנים לאדם.

לדוגמה, רוב המודלים של רגרסיה לינארית ניתנים לפירוש בקלות. (צריך רק לבדוק את המשקלים שאומנו לכל תכונה). בנוסף, קל מאוד לפרש את התוצאות של יערות החלטה. עם זאת, כדי להבין חלק מהמודלים צריך להשתמש בהדמיה מתוחכמת.

אפשר להשתמש בכלי לפרשנות של למידת מכונה (LIT) כדי לפרש מודלים של למידת מכונה.

איטרציה

#fundamentals

עדכון יחיד של הפרמטרים של מודל – המשקולות וההטיות של המודל – במהלך האימון. ההגדרה batch size קובעת כמה דוגמאות המודל מעבד באיטרציה אחת. לדוגמה, אם גודל האצווה הוא 20, המודל מעבד 20 דוגמאות לפני התאמת הפרמטרים.

כשמאמנים רשת נוירונים, איטרציה אחת כוללת את שני המעברים הבאים:

1. העברה קדימה להערכת הפסד באצווה אחת.
2. מעבר אחורה (backpropagation) כדי לשנות את הפרמטרים של המודל על סמך הפסד וקצב הלמידה.

מידע נוסף זמין במאמר בנושא Gradient descent בקורס המקוצר בנושא למידת מכונה.

L

רגולריזציה (regularization) מסוג L₀

#fundamentals

סוג של רגולריזציה שמעניש את המספר הכולל של משקלים שאינם אפס במודל. לדוגמה, מודל עם 11 משקלים שונים מאפס ייענש יותר ממודל דומה עם 10 משקלים שונים מאפס.

רגולריזציה מסוג L₀ נקראת לפעמים רגולריזציה מסוג L0-norm.

כדי לראות הערות נוספות, לוחצים על הסמל.

_{בדרך כלל, רגולריזציה מסוג L0 לא מעשית במודלים גדולים כי היא הופכת את האימון לבעיית אופטימיזציה קמורה.}

---

הפסד של ₁

#fundamentals

#Metric

פונקציית הפסד שמחשבת את הערך המוחלט של ההפרש בין ערכי התוויות בפועל לבין הערכים שהמודל חוזה. לדוגמה, כך מחשבים את הפסד L₁ עבור קבוצה של חמש דוגמאות:

ערך בפועל של הדוגמה	הערך שהמודל חזה	הערך המוחלט של השינוי
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		‫8 = הפסד L1

הפונקציה L₁ loss פחות רגישה לערכים חריגים מאשר הפונקציה _L2 loss.

השגיאה הממוצעת המוחלטת היא הפסד _L1 הממוצע לכל דוגמה.

כדי לראות את המתמטיקה הפורמלית, לוחצים על הסמל.

$$ L_1 loss = \sum_{i=0}^n | y_i - \hat{y}_i |$$

כאשר:

• ‫$n$ הוא מספר הדוגמאות.
• ‫$y$ הוא הערך בפועל של התווית.
• ‫$\hat{y}$ הוא הערך שהמודל חוזה עבור $y$.

---

מידע נוסף זמין במאמר Linear regression: Loss (רגרסיה לינארית: הפסד) בסדרת המאמרים Machine Learning Crash Course (מבוא ללמידת מכונה).

רגולריזציה מסוג L₁

#fundamentals

סוג של רגולריזציה שמענישה משקלים באופן יחסי לסכום הערך המוחלט של המשקלים. רגולריזציה מסוג L₁ עוזרת להקטין את המשקלים של תכונות לא רלוונטיות או רלוונטיות במידה מועטה ל-0 בדיוק. תכונה עם משקל 0 למעשה מוסרת מהמודל.

השוואה לרגולריזציה מסוג L₂.

הפסד L₂

#fundamentals

#Metric

פונקציית הפסד שמחשבת את ריבוע ההפרש בין ערכי התוויות בפועל לבין הערכים שהמודל חוזה. לדוגמה, הנה חישוב של הפסד L₂ עבור קבוצה של חמש דוגמאות:

ערך בפועל של הדוגמה	הערך שהמודל חזה	ריבוע של דלתא
7	6	1
5	4	1
8	11	9
4	6	4
9	8	1
		‫16 = L2 loss

בגלל ההעלאה בריבוע, הפסד L₂ מגביר את ההשפעה של ערכים חריגים. כלומר, הפסד L₂ מגיב בעוצמה רבה יותר לחיזויים לא טובים מאשר הפסד L₁. לדוגמה, ערך ההפסד L₁ עבור האצווה הקודמת יהיה 8 ולא 16. שימו לב שערך חריג אחד מייצג 9 מתוך 16.

מודלים של רגרסיה משתמשים בדרך כלל בהפסד L₂ כפונקציית ההפסד.

השגיאה הריבועית הממוצעת היא הפסד _L2 הממוצע לכל דוגמה. שגיאה בריבוע הוא שם נוסף לשגיאת L₂.

כדי לראות את המתמטיקה הפורמלית, לוחצים על הסמל.

$$ L_2 loss = \sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$

כאשר:

• ‫$n$ הוא מספר הדוגמאות.
• ‫$y$ הוא הערך בפועל של התווית.
• ‫$\hat{y}$ הוא הערך שהמודל חוזה עבור $y$.

---

מידע נוסף זמין במאמר Logistic regression: Loss and regularization (רגרסיה לוגיסטית: הפסד ורגולריזציה) בסדנה בנושא למידת מכונה.

רגולריזציה (regularization) של L₂

#fundamentals

סוג של רגולריזציה שמעניש משקלים באופן יחסי לסכום הריבועים של המשקלים. רגולריזציה מסוג L₂ עוזרת להסיט משקלים של ערכים חריגים (ערכים חיוביים גבוהים או ערכים שליליים נמוכים) קרוב יותר ל-0, אבל לא בדיוק ל-0. תכונות עם ערכים שקרובים מאוד ל-0 נשארות במודל, אבל לא משפיעות על התחזית של המודל.

רגולריזציה מסוג L₂ תמיד משפרת את ההכללה במודלים לינאריים.

השוואה לרגולריזציה מסוג _L1.

מידע נוסף זמין במאמר התאמת יתר: רגולריזציה מסוג L2 בקורס המקוצר על למידת מכונה.

תווית

#fundamentals

בלמידת מכונה מפוקחת, החלק של ה"תשובה" או ה "תוצאה" בדוגמה.

כל דוגמה מתויגת מורכבת ממאפיין אחד או יותר ומתווית. לדוגמה, במערך נתונים לזיהוי ספאם, התווית תהיה כנראה 'ספאם' או 'לא ספאם'. במערך נתונים של גשמים, התווית יכולה להיות כמות הגשם שירדה במהלך תקופה מסוימת.

מידע נוסף זמין במאמר Supervised Learning (למידה מפוקחת) בסדרה Introduction to Machine Learning (מבוא ללמידת מכונה).

דוגמה מסומנת בתווית

#fundamentals

דוגמה שמכילה תכונה אחת או יותר ותווית. לדוגמה, בטבלה הבאה מוצגות שלוש דוגמאות מתויגות ממודל להערכת שווי של בית, שלכל אחת מהן יש שלוש תכונות ותווית אחת:

מספר חדרי שינה	מספר חדרי אמבטיה	גיל הבית	מחיר הבית (תווית)
3	2	15	$345,000
2	1	72	$179,000
4	2	34	$392,000

בלמידת מכונה מבוקרת, מודלים מתאמנים על דוגמאות מתויגות ומבצעים חיזויים על דוגמאות לא מתויגות.

השוואה בין דוגמה עם תוויות לבין דוגמאות ללא תוויות.

מידע נוסף זמין במאמר Supervised Learning (למידה מפוקחת) בסדרה Introduction to Machine Learning (מבוא ללמידת מכונה).

lambda

#fundamentals

מילה נרדפת ל-regularization rate.

המונח Lambda הוא מונח עמוס. במאמר הזה אנחנו מתמקדים בהגדרה של המונח רגולריזציה.

שכבה

#fundamentals

קבוצה של נוירונים ברשת נוירונים. שלושה סוגים נפוצים של שכבות:

• שכבת הקלט, שמספקת ערכים לכל התכונות.
• שכבות מוסתרות אחת או יותר, שמוצאות קשרים לא לינאריים בין התכונות לבין התווית.
• שכבת הפלט, שמספקת את החיזוי.

לדוגמה, באיור הבא מוצג רשת עצבית עם שכבת קלט אחת, שתי שכבות נסתרות ושכבת פלט אחת:

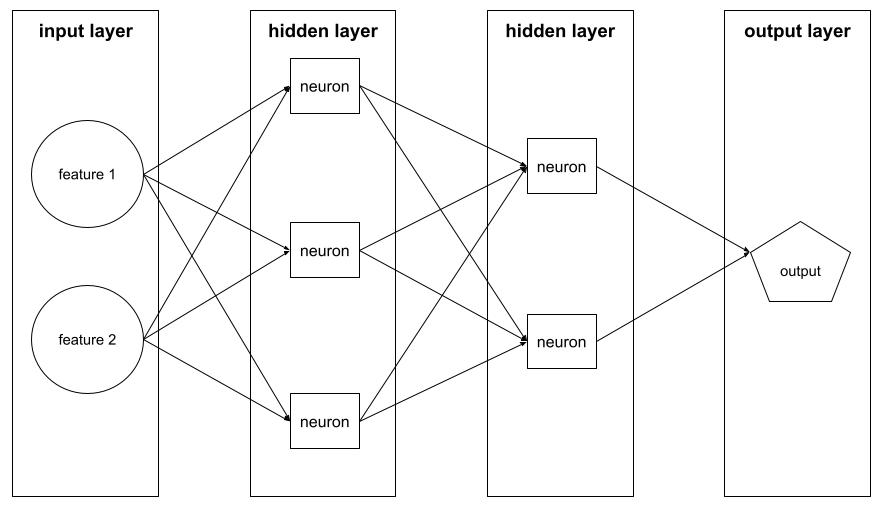
ב-TensorFlow, שכבות הן גם פונקציות Python שמקבלות טנסורים ואפשרויות הגדרה כקלט, ומפיקות טנסורים אחרים כפלט.

קצב למידה

#fundamentals

מספר נקודה צפה שמציין לאלגוריתם gradient descent עד כמה לשנות את המשקלים וההטיות בכל iteration. לדוגמה, שיעור למידה של 0.3 יתאים את המשקלים וההטיות בעוצמה גדולה פי 3 בהשוואה לשיעור למידה של 0.1.

קצב הלמידה הוא היפר-פרמטר מרכזי. אם מגדירים את קצב הלמידה נמוך מדי, האימון יימשך זמן רב מדי. אם קצב הלמידה מוגדר גבוה מדי, לרוב קשה להגיע להתכנסות בשיטת הגרדיאנט.

כדי לקבל הסבר מתמטי יותר, לוחצים על הסמל.

במהלך כל איטרציה, האלגוריתם gradient descent מכפיל את קצב הלמידה בשיפוע. המוצר שמתקבל נקרא צעד הגרדיאנט.

---

מידע נוסף זמין במאמר רגרסיה ליניארית: היפר-פרמטרים בקורס המקוצר על למידת מכונה.

ליניארי

#fundamentals

קשר בין שני משתנים או יותר שאפשר לייצג רק באמצעות חיבור וכפל.

הגרף של קשר לינארי הוא קו.

השוואה ללא לינארי.

מודל לינארי

#fundamentals

מודל שמקצה משקל אחד לכל מאפיין כדי ליצור תחזיות. (מודלים לינאריים כוללים גם הטיה). לעומת זאת, הקשר בין התכונות לבין התחזיות במודלים עמוקים הוא בדרך כלל לא לינארי.

בדרך כלל קל יותר לאמן מודלים לינאריים והם ניתנים יותר לפירוש ממודלים עמוקים. עם זאת, מודלים עמוקים יכולים ללמוד קשרים מורכבים בין תכונות.

רגרסיה לינארית ורגרסיה לוגיסטית הם שני סוגים של מודלים לינאריים.

כדי לראות את החישוב, לוחצים על הסמל.

מודל לינארי פועל לפי הנוסחה הבאה:

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

כאשר:

• ‫y' הוא החיזוי הגולמי. (בסוגים מסוימים של מודלים לינאריים, התחזית הגולמית הזו תעבור שינוי נוסף. לדוגמה, ראו רגרסיה לוגיסטית.)
• ‫b הוא ההטיה.
• ‫w הוא משקל, לכן w₁ הוא המשקל של התכונה הראשונה, w₂ הוא המשקל של התכונה השנייה וכן הלאה.
• ‫x הוא מאפיין, לכן x₁ הוא הערך של המאפיין הראשון, x₂ הוא הערך של המאפיין השני וכן הלאה.

לדוגמה, נניח שמודל לינארי עם שלוש תכונות לומד את ההטיה והמשקלים הבאים:

• b = 7
• ‫w₁ = -2.5
• w₂ = -1.2
• w₃ = 1.4

לכן, בהינתן שלוש תכונות (x₁, x₂ ו-x₃), המודל הליניארי משתמש במשוואה הבאה כדי ליצור כל תחזית:

y' = 7 + (-2.5)(x1) + (-1.2)(x2) + (1.4)(x3)

נניח שדוגמה מסוימת מכילה את הערכים הבאים:

• x₁ = 4
• x₂ = -10
• x₃ = 5

אם מציבים את הערכים האלה בנוסחה, מקבלים את התחזית הבאה לדוגמה הזו:

y' = 7 + (-2.5)(4) + (-1.2)(-10) + (1.4)(5)
y' = 16

מודלים ליניאריים כוללים לא רק מודלים שמשתמשים רק במשוואה ליניארית כדי ליצור תחזיות, אלא גם קבוצה רחבה יותר של מודלים שמשתמשים במשוואה ליניארית כרכיב אחד בלבד בנוסחה שיוצרת תחזיות. לדוגמה, רגרסיה לוגיסטית מבצעת עיבוד אחרי החיזוי הגולמי (y') כדי ליצור ערך חיזוי סופי בין 0 ל-1, לא כולל.

---

רגרסיה לינארית

#fundamentals

סוג של מודל למידת מכונה שבו מתקיימים שני התנאים הבאים:

• המודל הוא מודל לינארי.
• החיזוי הוא ערך נקודה צפה (floating-point). (זהו החלק של הרגרסיה ברגרסיה לינארית).

השוואה בין רגרסיה לינארית לבין רגרסיה לוגיסטית. כדאי גם להשוות בין רגרסיה לבין סיווג.

מידע נוסף זמין במאמר בנושא רגרסיה לינארית בקורס המקוצר על למידת מכונה.

רגרסיה לוגיסטית

#fundamentals

סוג של מודל רגרסיה שמנבא הסתברות. למודלים של רגרסיה לוגיסטית יש את המאפיינים הבאים:

• התווית היא קטגורית. המונח רגרסיה לוגיסטית מתייחס בדרך כלל לרגרסיה לוגיסטית בינארית, כלומר למודל שמחשב הסתברויות לתוויות עם שני ערכים אפשריים. וריאנט פחות נפוץ, רגרסיה לוגיסטית מולטינומיאלית, מחשב הסתברויות לתוויות עם יותר משני ערכים אפשריים.
• פונקציית ההפסד במהלך האימון היא Log Loss. (אפשר להציב כמה יחידות של Log Loss במקביל לתוויות עם יותר משני ערכים אפשריים).
• למודל יש ארכיטקטורה לינארית, ולא רשת עצבית עמוקה. עם זאת, שאר ההגדרה הזו חלה גם על מודלים עמוקים שמנבאים הסתברויות של תוויות קטגוריות.

לדוגמה, נניח שיש מודל רגרסיה לוגיסטית שמחשב את ההסתברות לכך שאימייל קלט הוא ספאם או לא ספאם. במהלך ההסקה, נניח שהמודל חוזה 0.72. לכן, המודל מעריך:

• סיכוי של 72% שהאימייל הוא ספאם.
• יש סיכוי של 28% שהאימייל לא ספאם.

מודל רגרסיה לוגיסטית משתמש בארכיטקטורה הבאה בת שני השלבים:

1. המודל יוצר חיזוי גולמי (y') על ידי החלת פונקציה לינארית של תכונות קלט.
2. המודל משתמש בתחזית הגולמית הזו כקלט לפונקציית סיגמואיד, שממירה את התחזית הגולמית לערך בין 0 ל-1, לא כולל.

בדומה לכל מודל רגרסיה, מודל רגרסיה לוגיסטית חוזה מספר. עם זאת, המספר הזה בדרך כלל הופך לחלק ממודל סיווג בינארי באופן הבא:

• אם המספר החזוי גדול מסף הסיווג, מודל הסיווג הבינארי חוזה את המחלקה החיובית.
• אם המספר החזוי נמוך מסף הסיווג, מודל הסיווג הבינארי חוזה את המחלקה השלילית.

מידע נוסף זמין במאמר רגרסיה לוגיסטית בקורס המקוצר על למידת מכונה.

אובדן לוגריתמי

#fundamentals

פונקציית ההפסד שמשמשת ברגרסיה לוגיסטית בינארית.

כדי לראות את החישוב, לוחצים על הסמל.

הנוסחה הבאה משמשת לחישוב של Log Loss:

$$\text{Log Loss} = \sum_{(x,y)\in D} -y\log(y') - (1 - y)\log(1 - y')$$

כאשר:

• ‫ \((x,y)\in D\) הוא מערך הנתונים שמכיל הרבה דוגמאות מתויגות, שהן זוגות של \((x,y)\) .
• ‫ \(y\) היא התווית בדוגמה המתויגת. מכיוון שמדובר ברגרסיה לוגיסטית, כל ערך של \(y\) חייב להיות 0 או 1.
• ‫ \(y'\) הוא הערך החזוי (בין 0 ל-1, לא כולל), בהינתן קבוצת התכונות ב- \(x\).

---

מידע נוסף זמין במאמר Logistic regression: Loss and regularization (רגרסיה לוגיסטית: אובדן ורגולריזציה) בסדנה בנושא למידת מכונה.

יחס הלוגים

#fundamentals

הלוגריתם של הסיכויים לאירוע מסוים.

כדי לראות את החישוב, לוחצים על הסמל.

אם האירוע הוא הסתברות בינארית, אז odds מתייחס ליחס בין ההסתברות להצלחה (p) לבין ההסתברות לכישלון (1-p). לדוגמה, נניח שלאירוע מסוים יש סיכוי של 90% להצלחה וסיכוי של 10% לכישלון. במקרה הזה, הסיכויים מחושבים כך:

$$ {\text{odds}} = \frac{\text{p}} {\text{(1-p)}} = \frac{.9} {.1} = {\text{9}} $$

הלוגריתם של הסיכויים הוא פשוט הלוגריתם של היחס בין הסיכויים. לפי המוסכמה, המונח 'לוגריתם' מתייחס ללוגריתם טבעי, אבל למעשה לוגריתם יכול להיות כל בסיס שגדול מ-1. בהתאם למוסכמה, הלוג-אודס של הדוגמה שלנו הוא:

$$ {\text{log-odds}} = ln(9) ~= 2.2 $$

פונקציית הלוג-אודס היא ההופכי של פונקציית הסיגמואיד.

---

ירידה

#fundamentals

#Metric

במהלך האימון של מודל בפיקוח, נמדד המרחק בין התחזית של המודל לבין התווית שלו.

פונקציית הפסד מחשבת את ההפסד.

מידע נוסף זמין במאמר רגרסיה ליניארית: הפסד בסדנה בנושא למידת מכונה.

עקומת הפסד

#fundamentals

תרשים של הפסד כפונקציה של מספר איטרציות האימון. התרשים הבא מציג עקומת הפסד אופיינית:

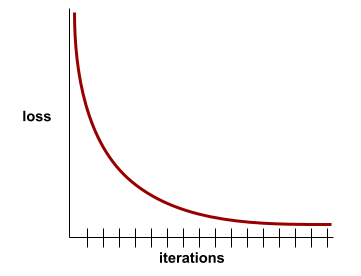
עקומות הפסד יכולות לעזור לכם לקבוע מתי המודל מתכנס או מתאים יתר על המידה.

עקומות הפסד יכולות להציג את כל סוגי ההפסד הבאים:

• הפסד האימון
• הפסד האימות
• test loss

אפשר לעיין גם בעקומת הכללה.

מידע נוסף מופיע במאמר התאמת יתר: פירוש עקומות הפסד בסדנה ללימוד מכונת למידה.

פונקציית אובדן

#fundamentals

#Metric

במהלך האימון או הבדיקה, פונקציה מתמטית שמחשבת את ההפסד באצווה של דוגמאות. פונקציית הפסד מחזירה ערך הפסד נמוך יותר למודלים שמבצעים חיזויים טובים מאשר למודלים שמבצעים חיזויים לא טובים.

המטרה של האימון היא בדרך כלל למזער את ההפסד שמוחזר על ידי פונקציית הפסד.

קיימים סוגים רבים ושונים של פונקציות אובדן. בוחרים את פונקציית ההפסד המתאימה לסוג המודל שאתם בונים. לדוגמה:

• הפונקציה אובדן _L2 (או השגיאה הריבועית הממוצעת) היא פונקציית האובדן של רגרסיה ליניארית.
• Log Loss היא פונקציית האובדן של רגרסיה לוגיסטית.

M

למידה חישובית

#fundamentals

תוכנה או מערכת שמאמנת מודל מנתוני קלט. המודל שעבר אימון יכול לבצע חיזויים שימושיים מנתונים חדשים (שלא נראו אף פעם) שנלקחו מאותו פיזור ששימש לאימון המודל.

למידת מכונה היא גם תחום המחקר שעוסק בתוכנות או במערכות האלה.

מידע נוסף זמין בקורס מבוא ללמידת מכונה.

מחלקה עם רוב

#fundamentals

התווית הנפוצה יותר במערך נתונים עם חוסר איזון בין מחלקות. לדוגמה, אם קבוצת נתונים מכילה 99% תוויות שליליות ו-1% תוויות חיוביות, התוויות השליליות הן מחלקת הרוב.

בניגוד לכיתת מיעוט.

מידע נוסף זמין במאמר מערכי נתונים: מערכי נתונים לא מאוזנים בסדנה ללימוד מכונתית.

מיני-batch

#fundamentals

קבוצת משנה קטנה שנבחרה באופן אקראי מתוך batch שעובר עיבוד באיטרציה אחת. גודל האצווה של אצווה קטנה הוא בדרך כלל בין 10 ל-1,000 דוגמאות.

לדוגמה, נניח שקבוצת האימון כולה (הקבוצה המלאה) כוללת 1,000 דוגמאות. נניח שאתם מגדירים את גודל האצווה של כל אצווה קטנה ל-20. לכן, בכל איטרציה נקבע ההפסד על סמך 20 דוגמאות אקראיות מתוך 1,000 הדוגמאות, ואז מתבצעים שינויים במשקלים ובהטיות בהתאם.

יעיל הרבה יותר לחשב את ההפסד במיני-אצווה מאשר לחשב את ההפסד בכל הדוגמאות באצווה המלאה.

מידע נוסף זמין במאמר רגרסיה ליניארית: היפר-פרמטרים בקורס המקוצר על למידת מכונה.

קבוצת מיעוט

#fundamentals

התווית הפחות נפוצה במערך נתונים לא מאוזן של מחלקות. לדוגמה, אם יש מערך נתונים שמכיל 99% תוויות שליליות ו-1% תוויות חיוביות, התוויות החיוביות הן המחלקה המיעוטית.

ההפך ממחלקת הרוב.

כדי לראות הערות נוספות, לוחצים על הסמל.

קבוצת אימון עם מיליון דוגמאות נשמעת מרשימה. עם זאת, אם הייצוג של המחלקה המיעוטית לא מספיק טוב, יכול להיות שגם מערך אימון גדול מאוד לא יספיק. חשוב להתמקד יותר במספר הדוגמאות בסיווג המיעוט, ולא במספר הכולל של הדוגמאות במערך הנתונים.

אם מערך הנתונים לא מכיל מספיק דוגמאות של מחלקת המיעוט, כדאי להשתמש בדילול (ההגדרה בתבליט השני) כדי להשלים את מחלקת המיעוט.

---

מידע נוסף זמין במאמר מערכי נתונים: מערכי נתונים לא מאוזנים בסדנה ללימוד מכונתית.

מודל

#fundamentals

באופן כללי, כל מבנה מתמטי שמעבד נתוני קלט ומחזיר פלט. במילים אחרות, מודל הוא קבוצת הפרמטרים והמבנה שדרושים למערכת כדי ליצור תחזיות. בלמידת מכונה מבוקרת, מודל מקבל דוגמה כקלט ומסיק חיזוי כפלט. בלמידת מכונה בפיקוח, יש הבדלים מסוימים בין המודלים. לדוגמה:

• מודל רגרסיה לינארית מורכב מקבוצה של משקלים ומהטיה.
• מודל של רשת נוירונים מורכב מ:
  • קבוצה של שכבות מוסתרות, שכל אחת מהן מכילה נוירון אחד או יותר.
  • המשקלים וההטיה שמשויכים לכל נוירון.
• מודל של עץ החלטה מורכב מ:
  • הצורה של העץ, כלומר התבנית שבה התנאים והעלים מחוברים.
  • התנאים והחופשות.

אפשר לשמור מודל, לשחזר אותו או ליצור ממנו עותקים.

למידת מכונה לא מפוקחת גם יוצרת מודלים, בדרך כלל פונקציה שיכולה למפות דוגמה של קלט לאשכול המתאים ביותר.

לוחצים על הסמל כדי להשוות בין פונקציות אלגבריות ופונקציות תכנות לבין מודלים של ML.

פונקציה אלגברית כמו הבאה היא מודל:

  f(x, y) = 3x -5xy + y2 + 17

הפונקציה הקודמת ממפה ערכי קלט (x ו-y) לפלט.

באופן דומה, פונקציית תכנות כמו הבאה היא גם מודל:

def half_of_greater(x, y):
  if (x > y):
    return(x / 2)
  else
    return(y / 2)

הפונקציה הקוראת מעבירה ארגומנטים לפונקציית Python הקודמת, ופונקציית Python יוצרת פלט (באמצעות ההצהרה return).

למרות שלרשת נוירונים עמוקה יש מבנה מתמטי שונה מאוד מזה של פונקציה אלגברית או פונקציית תכנות, היא עדיין מקבלת קלט (דוגמה) ומחזירה פלט (תחזית).

מתכנת אנושי מקודד פונקציית תכנות באופן ידני. לעומת זאת, מודל למידת מכונה לומד בהדרגה את הפרמטרים האופטימליים במהלך אימון אוטומטי.

---

סיווג רב-מחלקתי

#fundamentals

בלמידה מפוקחת, בעיית סיווג שבה מערך הנתונים מכיל יותר משני סוגים של תוויות. לדוגמה, התוויות במערך הנתונים של Iris צריכות להיות אחת משלוש המחלקות הבאות:

• Iris setosa
• Iris virginica
• Iris versicolor

מודל שאומן על מערך הנתונים של איריס ומנבא את סוג האיריס בדוגמאות חדשות, מבצע סיווג רב-מחלקתי.

לעומת זאת, בעיות סיווג שמבחינות בין שתי קטגוריות בדיוק הן מודלים של סיווג בינארי. לדוגמה, מודל אימייל שמנבא אם אימייל הוא ספאם או לא ספאם הוא מודל סיווג בינארי.

בבעיות של קיבוץ לאשכולות, סיווג רב-מחלקה מתייחס ליותר משני אשכולות.

מידע נוסף זמין במאמר רשתות עצביות: סיווג רב-מחלקתי בקורס המקוצר בנושא למידת מכונה.

לא

סיווג שלילי

#fundamentals

#Metric

בסיווג בינארי, מחלקים את הנתונים לשתי קבוצות: חיובית ושלילית. הסיווג החיובי הוא הדבר או האירוע שהמודל בודק, והסיווג השלילי הוא האפשרות השנייה. לדוגמה:

• הסיווג השלילי בבדיקה רפואית יכול להיות 'לא גידול'.
• הסיווג השלילי במודל סיווג של אימייל יכול להיות 'לא ספאם'.

ההגדרה הזו שונה מסיווג חיובי.

רשת הזרימה קדימה

#fundamentals

מודל שמכיל לפחות שכבה מוסתרת אחת. רשת עצבית עמוקה היא סוג של רשת עצבית שמכילה יותר משכבה נסתרת אחת. לדוגמה, בתרשים הבא מוצגת רשת עצבית עמוקה שמכילה שתי שכבות נסתרות.

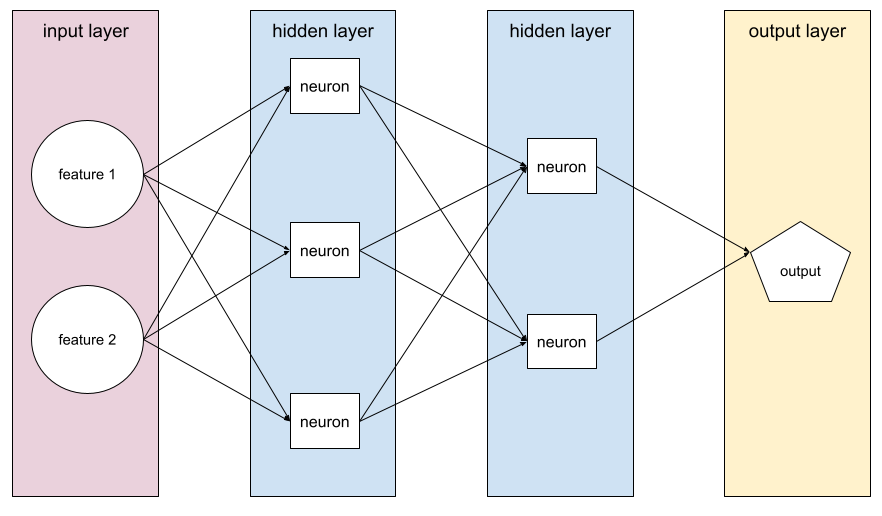
כל נוירון ברשת נוירונים מתחבר לכל הצמתים בשכבה הבאה. לדוגמה, בדיאגרמה הקודמת אפשר לראות שכל אחד משלושת הנוירונים בשכבה הנסתרת הראשונה מחובר בנפרד לשני הנוירונים בשכבה הנסתרת השנייה.

רשתות נוירונים שמיושמות במחשבים נקראות לפעמים רשתות נוירונים מלאכותיות כדי להבדיל ביניהן לבין רשתות נוירונים שנמצאות במוח ובמערכות עצבים אחרות.

חלק מהרשתות העצביות יכולות לחקות קשרים לא לינאריים מורכבים במיוחד בין תכונות שונות לבין התווית.

ראו גם רשת נוירונים מתקפלת ורשת נוירונים חוזרת.

מידע נוסף זמין במאמר רשתות עצביות בקורס המקוצר על למידת מכונה.

נוירון

#fundamentals

בלמידת מכונה, יחידה נפרדת בשכבה נסתרת של רשת נוירונים. כל נוירון מבצע את הפעולה הבאה בשני שלבים:

1. הפונקציה מחשבת את הסכום המשוקלל של ערכי הקלט כפול המשקלים התואמים שלהם.
2. הפונקציה מעבירה את הסכום המשוקלל כקלט לפונקציית הפעלה.

נוירון בשכבה הנסתרת הראשונה מקבל קלט מערכי המאפיינים בשכבת הקלט. נוירון בכל שכבה מוסתרת מעבר לשכבה הראשונה מקבל קלט מהנוירונים בשכבה המוסתרת הקודמת. לדוגמה, נוירון בשכבה הנסתרת השנייה מקבל קלט מהנוירונים בשכבה הנסתרת הראשונה.

באיור הבא אפשר לראות שני נוירונים והקלט שלהם.

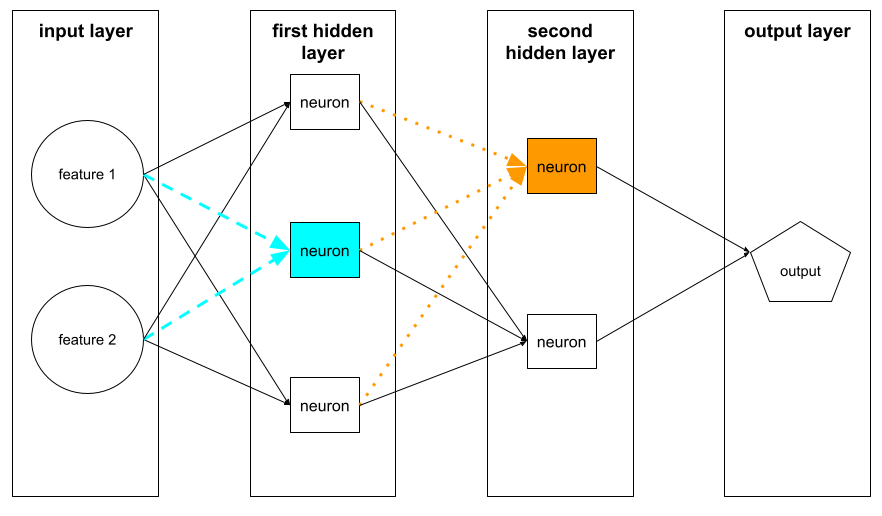
נוירון ברשת נוירונים מחקה את ההתנהגות של נוירונים במוח ובחלקים אחרים של מערכת העצבים.

צומת (רשת נוירונים)

#fundamentals

נוירון בשכבה נסתרת.

מידע נוסף מופיע במאמר רשתות עצביות בקורס המקוצר על למידת מכונה.

לא לינארי

#fundamentals

קשר בין שני משתנים או יותר שלא ניתן לייצג רק באמצעות חיבור וכפל. אפשר לייצג קשר לינארי באמצעות קו, אבל אי אפשר לייצג קשר לא לינארי באמצעות קו. לדוגמה, נניח שיש שני מודלים שכל אחד מהם מקשר בין תכונה אחת לתווית אחת. המודל בצד ימין הוא ליניארי והמודל בצד שמאל הוא לא ליניארי:

בקורס המקוצר בנושא למידת מכונה, אפשר לעיין בקטע רשתות עצביות: צמתים ושכבות מוסתרות כדי להתנסות בסוגים שונים של פונקציות לא לינאריות.

nonstationarity

#fundamentals

תכונה שהערכים שלה משתנים לאורך מאפיין אחד או יותר, בדרך כלל זמן. לדוגמה, שימו לב לדוגמאות הבאות של אי-סטציונריות:

• מספר בגדי הים שנמכרים בחנות מסוימת משתנה בהתאם לעונה.
• הכמות של פרי מסוים שנקטף באזור מסוים היא אפס במשך רוב השנה, אבל גדולה לתקופה קצרה.
• בגלל שינויי האקלים, הטמפרטורות הממוצעות השנתיות משתנות.

הניגוד לסטציונריות.

נירמול

#fundamentals

באופן כללי, תהליך ההמרה של טווח הערכים בפועל של משתנה לטווח ערכים סטנדרטי, כמו:

• ‫‎-1 עד ‎+1
• ‫0 עד 1
• ציוני תקן (בערך, ‎-3 עד ‎+3)

לדוגמה, נניח שהטווח בפועל של ערכי תכונה מסוימת הוא 800 עד 2,400. כחלק מהנדסת התכונות, אפשר לנרמל את הערכים בפועל לטווח סטנדרטי, למשל מ-1 עד +1.

נורמליזציה היא משימה נפוצה בהנדסת תכונות. בדרך כלל, אימון המודלים מהיר יותר (והתחזיות מדויקות יותר) כשכל תכונה מספרית בווקטור התכונות נמצאת בטווח דומה.

אפשר לעיין גם במאמר נורמליזציה של ציון תקן.

מידע נוסף זמין במאמר נתונים מספריים: נורמליזציה בסדנה ללימוד למידת מכונה.

נתונים מספריים

#fundamentals

מאפיינים שמיוצגים כמספרים שלמים או כמספרים ממשיים. לדוגמה, במודל להערכת שווי של בית, גודל הבית (במטרים רבועים או ברגל רבוע) כנראה ייוצג כנתונים מספריים. ייצוג של תכונה כנתונים מספריים מציין שלערכים של התכונה יש קשר מתמטי לתווית. כלומר, למספר המטרים הרבועים בבית יש כנראה קשר מתמטי כלשהו לערך הבית.

לא כל נתוני המספרים השלמים צריכים להיות מיוצגים כנתונים מספריים. לדוגמה, מיקודים בחלקים מסוימים בעולם הם מספרים שלמים, אבל מיקודים שהם מספרים שלמים לא צריכים להיות מיוצגים כנתונים מספריים במודלים. הסיבה לכך היא שמיקוד של 20000 לא חזק פי שניים (או חצי) ממיקוד של 10000. בנוסף, למרות שיש קשר בין מיקודים שונים לבין ערכי נדל"ן שונים, אי אפשר להניח שערכי הנדל"ן במיקוד 20000 הם כפולים מערכי הנדל"ן במיקוד 10000. במקום זאת, צריך להציג את המיקודים כנתונים קטגוריים.

תכונות מספריות נקראות לפעמים תכונות רציפות.

מידע נוסף זמין במאמר עבודה עם נתונים מספריים בקורס המקוצר על למידת מכונה.

O

לא מקוון

#fundamentals

מילה נרדפת ל-static.

הסקת מסקנות אופליין

#fundamentals

התהליך שבו מודל יוצר קבוצה של חיזויים ואז שומר אותם במטמון. לאחר מכן, האפליקציות יכולות לגשת לתחזית המשוערת מהמטמון במקום להפעיל מחדש את המודל.

לדוגמה, נניח שיש מודל שמפיק תחזיות מזג אוויר מקומיות (חיזויים) פעם בארבע שעות. אחרי כל הרצת מודל, המערכת שומרת במטמון את כל התחזיות המקומיות. אפליקציות מזג האוויר מאחזרות את התחזיות מהמטמון.

הסקת מסקנות אופליין נקראת גם הסקת מסקנות סטטית.

השוואה להסקת מסקנות אונליין. מידע נוסף זמין במאמר מערכות ML לייצור: הסקה סטטית לעומת הסקה דינמית בתוכנית Machine Learning Crash Course.

קידוד one-hot

#fundamentals

ייצוג נתונים קטגוריים כווקטור שבו:

• רכיב אחד מוגדר ל-1.
• כל שאר הרכיבים מוגדרים כ-0.

קידוד one-hot משמש בדרך כלל לייצוג מחרוזות או מזהים שיש להם קבוצה סופית של ערכים אפשריים. לדוגמה, נניח שלתכונה קטגורית מסוימת בשם Scandinavia יש חמישה ערכים אפשריים:

• "דנמרק"
• "Sweden"
• "Norway"
• "Finland"
• "איסלנד"

קידוד one-hot יכול לייצג כל אחד מחמשת הערכים באופן הבא:

מדינה	וקטור
"דנמרק"	1	0	0	0	0
"Sweden"	0	1	0	0	0
"Norway"	0	0	1	0	0
"Finland"	0	0	0	1	0
"איסלנד"	0	0	0	0	1

הודות לקידוד one-hot, מודל יכול ללמוד קשרים שונים על סמך כל אחת מחמש המדינות.

ייצוג מאפיין כנתונים מספריים הוא חלופה לקידוד "חם-יחיד". לצערנו, לא מומלץ לייצג את המדינות הסקנדינביות באמצעות מספרים. לדוגמה, הנה ייצוג מספרי:

• ‫"Denmark" הוא 0
• ‫"Sweden" הוא 1
• ‫"Norway" הוא 2
• ‫"Finland" הוא 3
• ‫"Iceland" הוא 4

בקידוד מספרי, המודל יפרש את המספרים הגולמיים באופן מתמטי וינסה להתאמן על המספרים האלה. עם זאת, איסלנד לא גדולה פי שניים (או קטנה פי שניים) מנורווגיה, ולכן המודל יגיע למסקנות מוזרות.

מידע נוסף זמין במאמר נתונים קטגוריים: אוצר מילים וקידוד one-hot בסדנה ללימוד למידת מכונה.

אחד מול כולם

#fundamentals

בהינתן בעיית סיווג עם N מחלקות, פתרון שמורכב ממודל סיווג בינארי נפרד של N – מודל סיווג בינארי אחד לכל תוצאה אפשרית. לדוגמה, אם יש מודל שמסווג דוגמאות כבעלי חיים, ירקות או מינרלים, פתרון של אחד מול כולם יספק את שלושת המודלים הנפרדים הבאים של סיווג בינארי:

• בעל חיים לעומת לא בעל חיים
• ירק לעומת לא ירק
• מינרל לעומת לא מינרל

online

#fundamentals

מילה נרדפת לדינמי.

היקש אונליין

#fundamentals

יצירת תחזיות לפי דרישה. לדוגמה, נניח שאפליקציה מעבירה קלט למודל ושולחת בקשה לתחזית. מערכת שמשתמשת בהסקת מסקנות אונליין מגיבה לבקשה על ידי הפעלת המודל (ומחזירה את החיזוי לאפליקציה).

ההבדל בין הסקת מסקנות אופליין לבין הסקת מסקנות אונליין.

מידע נוסף זמין במאמר מערכות ML לייצור: הסקה סטטית לעומת הסקה דינמית בתוכנית Machine Learning Crash Course.

שכבת הפלט

#fundamentals

השכבה ה'הסופית' של רשת נוירונים. שכבת הפלט מכילה את החיזוי.

האיור הבא מציג רשת עצבית עמוקה קטנה עם שכבת קלט, שתי שכבות נסתרות ושכבת פלט:

התאמת יתר (overfitting)

#fundamentals

יצירת מודל שתואם לנתוני האימון בצורה כל כך מדויקת, שהמודל לא מצליח לבצע חיזויים נכונים לגבי נתונים חדשים.

רגולריזציה יכולה לצמצם את התאמת היתר. אימון על מערך אימון גדול ומגוון יכול גם להפחית את התאמת היתר.

כדי לראות הערות נוספות, לוחצים על הסמל.

התאמת יתר היא כמו לפעול לפי העצות של המורה האהוב עליך בלבד. סביר להניח שתצליחו בכיתה של המורה הזה, אבל יכול להיות שתתאימו את עצמכם יותר מדי לרעיונות של המורה ולא תצליחו בכיתות אחרות. אם תקשיבו לעצות של מורים שונים, תוכלו להסתגל טוב יותר למצבים חדשים.

---

מידע נוסף מופיע במאמר בנושא התאמת יתר בקורס המקוצר על למידת מכונה.

P

פנדות

#fundamentals

‫API לניתוח נתונים מבוסס-עמודות, שמבוסס על numpy. הרבה מסגרות של למידת מכונה, כולל TensorFlow, תומכות במבני נתונים של pandas כקלט. פרטים נוספים זמינים במסמכי התיעוד של pandas.

פרמטר

#fundamentals

המשקולות וההטיות שהמודל לומד במהלך האימון. לדוגמה, במודל רגרסיה לינארית, הפרמטרים מורכבים מההטיה (b) ומכל המשקלים (w₁,‏ w₂ וכן הלאה) בנוסחה הבאה:

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

לעומת זאת, היפר-פרמטרים הם הערכים שאתם (או שירות להתאמת היפר-פרמטרים) מספקים למודל. לדוגמה, קצב הלמידה הוא היפר-פרמטר.

סיווג חיובי

#fundamentals

#Metric

הכיתה שאתם נבחנים בה.

לדוגמה, המחלקה החיובית במודל לסרטן יכולה להיות 'גידול'. הסיווג החיובי במודל סיווג של אימייל יכול להיות 'ספאם'.

ההפך מכיתה שלילית.

כדי לראות הערות נוספות, לוחצים על הסמל.

המונח סיווג חיובי עלול לבלבל, כי התוצאה ה'חיובית' של הרבה בדיקות היא לרוב תוצאה לא רצויה. לדוגמה, הסיווג החיובי בהרבה בדיקות רפואיות מתאים לגידולים או למחלות. באופן כללי, אתם רוצים לשמוע מרופא את המילים: "מזל טוב! תוצאות הבדיקה שלך היו שליליות". בכל מקרה, המחלקה החיובית היא האירוע שהבדיקה מנסה למצוא.

אמנם, אתם בודקים בו-זמנית את המחלקות החיוביות והשליליות.

---

עיבוד תמונה (Post Processing)

#responsible

#fundamentals

שינוי הפלט של מודל אחרי שהמודל הופעל. אפשר להשתמש בעיבוד שלאחר מכן כדי לאכוף אילוצי הוגנות בלי לשנות את המודלים עצמם.

לדוגמה, אפשר להחיל עיבוד אחרי על מודל סיווג בינארי על ידי הגדרת סף סיווג כך ששוויון הזדמנויות יישמר עבור מאפיין מסוים. כדי לעשות זאת, צריך לוודא ששיעור החיוביים האמיתיים זהה לכל הערכים של אותו מאפיין.

דיוק

#fundamentals

#Metric

מדד למודלים של סיווג שעונה על השאלה הבאה:

כשהמודל חזה את הסיווג החיובי, מה אחוז החיזויים הנכונים?

זו הנוסחה:

$$\text{Precision} = \frac{\text{true positives}} {\text{true positives} + \text{false positives}}$$

where:‎

• חיובי אמיתי פירושו שהמודל חזה נכון את המחלקה החיובית.
• תוצאה חיובית שגויה פירושה שהמודל טעה וחיזוי את הסיווג החיובי.

לדוגמה, נניח שמודל יצר 200 תחזיות חיוביות. מתוך 200 התחזיות החיוביות האלה:

• 150 היו חיוביים אמיתיים.
• 50 מהן היו תוצאות חיוביות שגויות.

במקרה זה:

$$\text{Precision} = \frac{\text{150}} {\text{150} + \text{50}} = 0.75$$

ההגדרה הזו שונה מדיוק ומהחזרה.

מידע נוסף זמין במאמר בנושא סיווג: דיוק, היזכרות, פרסיזיה ומדדים קשורים בסדנה ללמידת מכונה.

חיזוי (prediction)

#fundamentals

הפלט של המודל. לדוגמה:

• החיזוי של מודל סיווג בינארי הוא או הסיווג החיובי או הסיווג השלילי.
• החיזוי של מודל סיווג רב-מחלקתי הוא מחלקה אחת.
• החיזוי של מודל רגרסיה לינארית הוא מספר.

תוויות לשרת proxy

#fundamentals

הנתונים שמשמשים לחישוב משוער של התוויות לא זמינים ישירות במערך נתונים.

לדוגמה, נניח שאתם צריכים לאמן מודל כדי לחזות את רמת הלחץ של העובדים. מערך הנתונים מכיל הרבה תכונות חיזוי, אבל לא מכיל תווית בשם stress level. אתם לא מתייאשים ובוחרים בתווית 'תאונות במקום העבודה' כתווית חלופית לרמת הלחץ. בסופו של דבר, עובדים שנמצאים במתח גבוה מעורבים ביותר תאונות מעובדים רגועים. או שכן? יכול להיות שתאונות במקומות עבודה עולות ויורדות בפועל מכמה סיבות.

דוגמה נוספת: נניח שאתם רוצים ש-is it raining? יהיה תווית בוליאנית למערך הנתונים, אבל מערך הנתונים לא מכיל נתוני גשם. אם יש תמונות זמינות, יכול להיות שתגדירו תמונות של אנשים עם מטריות כתווית פרוקסי לשאלה is it raining? (האם יורד גשם?). האם זו תווית טובה לשימוש כפרוקסי? יכול להיות, אבל אנשים בתרבויות מסוימות נוטים יותר לשאת מטרייה כדי להגן על עצמם מפני השמש ולא מפני הגשם.

תוויות של שרתי proxy הן לרוב לא מושלמות. במידת האפשר, עדיף לבחור תוויות בפועל ולא תוויות פרוקסי. עם זאת, אם אין תווית בפועל, צריך לבחור את תווית הפרוקסי בזהירות רבה, ולבחור את תווית הפרוקסי שהיא הכי פחות גרועה מבין האפשרויות.

מידע נוסף זמין במאמר Datasets: Labels (קבוצות נתונים: תוויות) בקורס המקוצר על למידת מכונה.

R

RAG

#fundamentals

קיצור של retrieval-augmented generation (גנרציה מועשרת באחזור).

מעריך

#fundamentals

אדם שמספק תוויות לדוגמאות. 'מבאר' הוא שם נוסף ל'מדרג'.

מידע נוסף זמין במאמר נתונים קטגוריים: בעיות נפוצות בסדנת Machine Learning.

recall

#fundamentals

#Metric

מדד למודלים של סיווג שעונה על השאלה הבאה:

כאשר האמת הבסיסית הייתה הסיווג החיובי, מהו אחוז התחזיות שהמודל זיהה נכון כסיווג החיובי?

זו הנוסחה:

\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]

where:‎

• חיובי אמיתי פירושו שהמודל חזה נכון את המחלקה החיובית.
• תוצאה שלילית שגויה פירושה שהמודל טעה וחיזה את הסיווג השלילי.

לדוגמה, נניח שהמודל שלכם יצר 200 תחזיות לגבי דוגמאות שבהן האמת הבסיסית הייתה הסיווג החיובי. מתוך 200 התחזיות האלה:

• 180 היו תוצאות חיוביות אמיתיות.
• 20 מהן היו תוצאות שליליות מטעות.

במקרה זה:

\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]

לוחצים על הסמל כדי לראות הערות לגבי מערכי נתונים עם חוסר איזון בין הכיתות.

המדד Recall שימושי במיוחד לקביעת יכולת החיזוי של מודלים לסיווג שבהם המחלקה החיובית היא נדירה. לדוגמה, נניח שיש מערך נתונים עם חוסר איזון בין המחלקות שבו המחלקה החיובית למחלה מסוימת מופיעה רק אצל 10 מתוך מיליון מטופלים. נניח שהמודל שלכם מבצע חמישה מיליון חיזויים שמניבים את התוצאות הבאות:

• ‫30 חיוביים אמיתיים
• 20 תוצאות שליליות כוזבות
• ‫4,999,000 תוצאות שליליות אמיתיות
• 950 תוצאות חיוביות שגויות

לכן, ה-recall של המודל הזה הוא:

recall = TP / (TP + FN)
recall = 30 / (30 + 20) = 0.6 = 60%

לעומת זאת, רמת הדיוק של המודל הזה היא:

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (30 + 4,999,000) / (30 + 4,999,000 + 950 + 20) = 99.98%

ערך הדיוק הגבוה הזה נראה מרשים, אבל הוא חסר משמעות. המדד Recall שימושי הרבה יותר למערכי נתונים לא מאוזנים מבחינת כמות הנתונים בכל מחלקה מאשר המדד Accuracy.

---

מידע נוסף זמין במאמר סיווג: דיוק, היזכרות, פרסיזיה ומדדים קשורים.

יחידה לינארית מתוקנת (ReLU)

#fundamentals

פונקציית הפעלה עם ההתנהגות הבאה:

• אם הקלט שלילי או אפס, הפלט הוא 0.
• אם הקלט חיובי, הפלט שווה לקלט.

לדוגמה:

• אם הקלט הוא ‎-3, הפלט הוא 0.
• אם הקלט הוא ‎+3, הפלט הוא 3.0.

הנה גרף של ReLU:

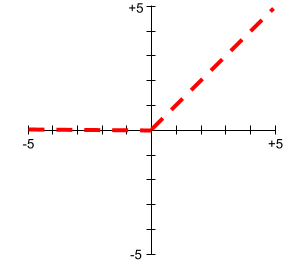
‫ReLU היא פונקציית הפעלה פופולרית מאוד. למרות ההתנהגות הפשוטה שלה, ReLU עדיין מאפשרת לרשת נוירונים ללמוד על קשרים לא לינאריים בין תכונות לבין התווית.

מודל רגרסיה

#fundamentals

באופן לא רשמי, מודל שיוצר חיזוי מספרי. (לעומת זאת, מודל סיווג יוצר חיזוי של סיווג.) לדוגמה, כל המודלים הבאים הם מודלים של רגרסיה:

• מודל שמנבא את הערך של בית מסוים באירו, למשל 423,000.
• מודל שמנבא את תוחלת החיים של עץ מסוים בשנים, למשל 23.2.
• מודל שמנבא את כמות הגשם באינצ'ים שתירד בעיר מסוימת במהלך שש השעות הבאות, למשל 0.18.

שני סוגים נפוצים של מודלים של רגרסיה הם:

• רגרסיה לינארית, שמוצאת את הקו שהכי מתאים לערכי התוויות ולמאפיינים.
• רגרסיה לוגיסטית, שמפיקה הסתברות בין 0.0 ל-1.0, שבדרך כלל ממופה על ידי המערכת לחיזוי של סיווג.

לא כל מודל שמפיק תחזיות מספריות הוא מודל רגרסיה. במקרים מסוימים, חיזוי מספרי הוא למעשה מודל סיווג עם שמות מחלקות מספריים. לדוגמה, מודל שמנבא מיקוד מספרי הוא מודל סיווג ולא מודל רגרסיה.

רגולריזציה (regularization)

#fundamentals

כל מנגנון שמפחית התאמת יתר. סוגים פופולריים של רגולריזציה כוללים:

• רגולריזציה מסוג L₁
• רגולריזציה מסוג _L2
• dropout regularization
• עצירה מוקדמת (זו לא שיטה רשמית של רגולריזציה, אבל היא יכולה להגביל ביעילות את התאמת היתר)

אפשר גם להגדיר רגולריזציה כעונש על מורכבות של מודל.

כדי לראות הערות נוספות, לוחצים על הסמל.

הרגולריזציה היא לא אינטואיטיבית. הגדלת הרגולריזציה בדרך כלל מגדילה את הפסד האימון, וזה מבלבל כי המטרה היא למזער את הפסד האימון.

למעשה, לא. המטרה היא לא למזער את הפסד האימון. המטרה היא ליצור תחזיות מצוינות על דוגמאות מהעולם האמיתי. חשוב לציין שאף על פי שהגדלת הרגולריזציה מגדילה את אובדן האימון, היא בדרך כלל עוזרת למודלים לבצע תחזיות טובות יותר בדוגמאות מהעולם האמיתי.

---

מידע נוסף זמין במאמר התאמת יתר: מורכבות המודל בקורס המקוצר על למידת מכונה.

שיעור הרגולריזציה

#fundamentals

מספר שמציין את החשיבות היחסית של רגולריזציה במהלך האימון. העלאת שיעור הרגולריזציה מפחיתה את ההתאמה העודפת, אבל עשויה להפחית את יכולת החיזוי של המודל. לעומת זאת, הקטנה של שיעור הרגולריזציה או השמטה שלו מגדילות את התאמת היתר.

כדי לראות את החישוב, לוחצים על הסמל.

שיעור הרגולריזציה מיוצג בדרך כלל באמצעות האות היוונית למדא. המשוואה הפשוטה הבאה של loss מראה את ההשפעה של lambda:

$$\text{minimize(loss function + }\lambda\text{(regularization))}$$

כאשר regularization הוא כל מנגנון regularization, כולל:

• רגולריזציה מסוג L₁
• רגולריזציה מסוג _L2

---

מידע נוסף זמין במאמר התאמת יתר: רגולריזציה מסוג L2 בקורס המקוצר על למידת מכונה.

ReLU

#fundamentals

קיצור של Rectified Linear Unit (יחידה לינארית מתוקנת).

שיפור התשובות בעזרת אחזור מידע (RAG)

#fundamentals

טכניקה לשיפור האיכות של הפלט של מודל שפה גדול (LLM) על ידי ביסוסו על מקורות ידע שאוחזרו אחרי שהמודל אומן. ‫RAG משפר את הדיוק של התשובות של LLM בכך שהוא מספק ל-LLM המאומן גישה למידע שאוחזר ממסמכים או מבסיסי ידע מהימנים.

הנה כמה מהסיבות הנפוצות לשימוש ב-RAG:

• שיפור הדיוק העובדתי של התשובות שהמודל יוצר.
• מתן גישה למודל לידע שהוא לא אומן עליו.
• שינוי הידע שבו המודל משתמש.
• הפעלת האפשרות לציטוט מקורות על ידי המודל.

לדוגמה, נניח שאפליקציה ללימוד כימיה משתמשת ב-PaLM API כדי ליצור סיכומים שקשורים לשאילתות של משתמשים. כשחלק הקצה העורפי של האפליקציה מקבל שאילתה, הוא:

1. מחפש (או מאחזר) נתונים שרלוונטיים לשאילתה של המשתמש.
2. מצרף ("מרחיב") את נתוני הכימיה הרלוונטיים לשאילתה של המשתמש.
3. ההנחיה הזו גורמת ל-LLM ליצור סיכום על סמך הנתונים שנוספו.

עקומת ROC (מאפיין הפעולה של המקלט)

#fundamentals

#Metric

תרשים של שיעור החיוביים האמיתיים לעומת שיעור החיוביים הכוזבים עבור ערכי סף שונים לסיווג בסיווג בינארי.

הצורה של עקומת ROC מצביעה על היכולת של מודל סיווג בינארי להפריד בין סיווגים חיוביים לסיווגים שליליים. נניח, לדוגמה, שמודל סיווג בינארי מפריד בצורה מושלמת בין כל המחלקות השליליות לבין כל המחלקות החיוביות:

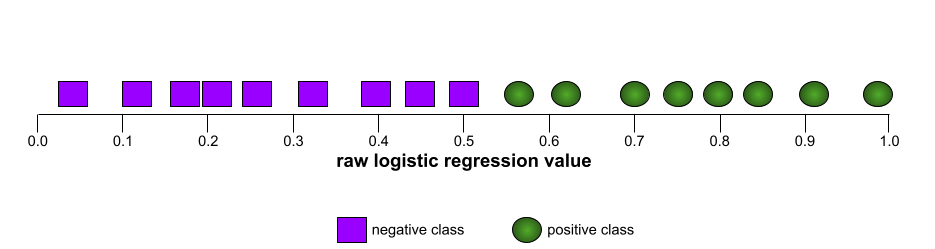
עקומת ה-ROC של המודל הקודם נראית כך:

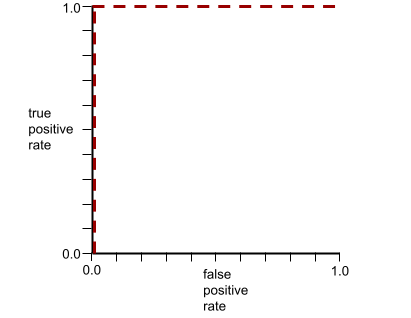
לעומת זאת, באיור הבא מוצגים ערכי הרגרסיה הלוגיסטית הגולמיים של מודל גרוע שלא מצליח להפריד בין מחלקות שליליות למחלקות חיוביות:

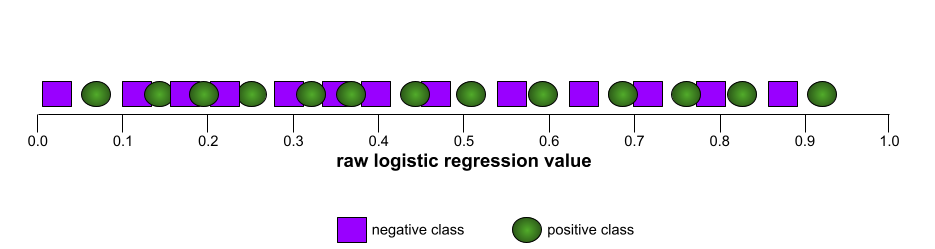
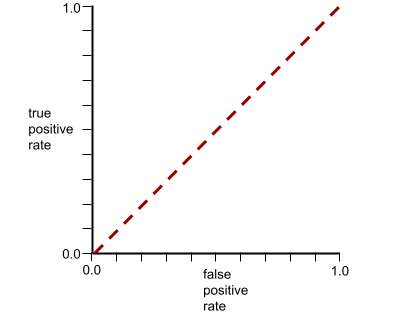
עקומת ה-ROC של המודל הזה נראית כך:

בינתיים, בעולם האמיתי, רוב מודלי הסיווג הבינארי מפרידים בין מחלקות חיוביות ושליליות במידה מסוימת, אבל בדרך כלל לא בצורה מושלמת. לכן, עקומת ROC אופיינית נמצאת איפשהו בין שני הקצוות:

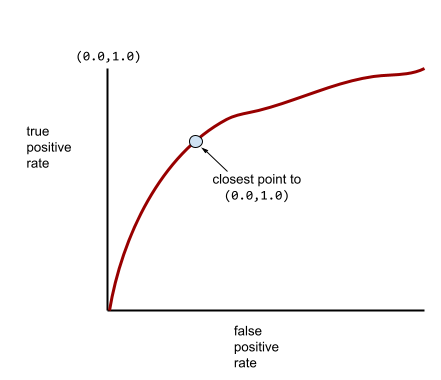
הנקודה בעקומת ROC שהכי קרובה ל-(0.0,1.0) מזהה באופן תיאורטי את סף הסיווג האידיאלי. עם זאת, יש כמה בעיות בעולם האמיתי שמשפיעות על הבחירה של סף הסיווג האידיאלי. לדוגמה, יכול להיות שתוצאות שליליות כוזבות גורמות להרבה יותר נזק מתוצאות חיוביות כוזבות.

מדד מספרי שנקרא AUC מסכם את עקומת ה-ROC לערך יחיד של נקודה צפה.

שורש טעות ריבועית ממוצעת (RMSE)

#fundamentals

#Metric

השורש הריבועי של הטעות הריבועית הממוצעת.

S

פונקציית סיגמואיד

#fundamentals

פונקציה מתמטית ש'דוחסת' ערך קלט לטווח מוגבל, בדרך כלל 0 עד 1 או ‎-1 עד ‎+1. כלומר, אפשר להעביר כל מספר (שניים, מיליון, מינוס מיליארד, מה שרוצים) לפונקציית הסיגמואיד, והפלט עדיין יהיה בטווח המוגבל. גרף של פונקציית ההפעלה הסיגמואידית נראה כך:

לפונקציית הסיגמואיד יש כמה שימושים בלמידת מכונה, כולל:

• המרת הפלט הגולמי של מודל רגרסיה לוגיסטית או רגרסיה מולטינומיאלית להסתברות.
• פועלת כפונקציית הפעלה בחלק מהרשתות העצביות.

כדי לראות את החישוב, לוחצים על הסמל.

הנוסחה של פונקציית הסיגמואיד על מספר קלט x היא:

$$ sigmoid(x) = \frac{1}{1 + e^{-\text{x}}} $$

בלמידת מכונה, x הוא בדרך כלל סכום משוקלל.

---

softmax

#fundamentals

פונקציה שקובעת הסתברויות לכל מחלקה אפשרית במודל סיווג רב-מחלקה. סכום ההסתברויות הוא בדיוק 1.0. לדוגמה, הטבלה הבאה מראה איך פונקציית softmax מחלקת הסתברויות שונות:

התמונה היא…	Probability
כלב	‫0.85
cat	‫.13
סוס	‫.02

‫Softmax נקרא גם full softmax.

ההבדל בין זה לבין דגימת מועמדים.

כדי לראות את החישוב, לוחצים על הסמל.

המשוואה של softmax היא:

$$\sigma_i = \frac{e^{\text{z}_i}} {\sum_{j=1}^{j=K} {e^{\text{z}_j}}} $$

כאשר:

• ‫$\sigma_i$ הוא וקטור הפלט. כל רכיב של וקטור הפלט מציין את ההסתברות של הרכיב הזה. סכום כל הרכיבים בווקטור הפלט הוא 1.0. וקטור הפלט מכיל את אותו מספר רכיבים כמו וקטור הקלט, ‎$z$‎.
• ‫$z$ הוא וקטור הקלט. כל רכיב של וקטור הקלט מכיל ערך של נקודה צפה.
• ‫$K$ הוא מספר הרכיבים בווקטור הקלט (ובווקטור הפלט).

לדוגמה, נניח שווקטור הקלט הוא:

[1.2, 2.5, 1.8]

לכן, פונקציית softmax מחשבת את המכנה באופן הבא:

$$\text{denominator} = e^{1.2} + e^{2.5} + e^{1.8} = 21.552$$

לכן, ההסתברות של כל אלמנט ב-softmax היא:

$$\sigma_1 = \frac{e^{1.2}}{21.552} = 0.154 $$ $$\sigma_2 = \frac{e^{2.5}}{21.552} = 0.565 $$ $$\sigma_1 = \frac{e^{1.8}}{21.552} = 0.281 $$

לכן, וקטור הפלט הוא:

$$\sigma = [0.154, 0.565, 0.281]$$

סכום שלושת הרכיבים ב-$\sigma$ הוא 1.0. סוף סוף!

---

מידע נוסף זמין במאמר רשתות עצביות: סיווג רב-מחלקתי בקורס המקוצר בנושא למידת מכונה.

תכונה דלילה

#fundamentals

תכונה שהערכים שלה הם בעיקר אפס או ריקים. לדוגמה, תכונה שמכילה ערך אחד של 1 ומיליון ערכים של 0 היא דלילה. לעומת זאת, לתכונה צפופה יש ערכים שהם בעיקר לא אפס או לא ריקים.

בלמידת מכונה, מספר מפתיע של מאפיינים הם מאפיינים דלילים. תכונות קטגוריות הן בדרך כלל תכונות דלילות. לדוגמה, מתוך 300 מיני עצים אפשריים ביער, דוגמה אחת יכולה לזהות רק עץ אדר. או מתוך מיליוני הסרטונים האפשריים בספריית סרטונים, דוגמה אחת עשויה לזהות רק את הסרט 'קזבלנקה'.

במודל, בדרך כלל מייצגים מאפיינים דלילים באמצעות קידוד חם-יחיד. אם הקידוד מסוג "חם-יחיד" גדול, אפשר להוסיף שכבת הטמעה מעל הקידוד מסוג "חם-יחיד" כדי לשפר את היעילות.

ייצוג דליל

#fundamentals

אחסון רק של המיקומים של רכיבים שאינם אפס בתכונה דלילה.

לדוגמה, נניח שיש תכונה קטגורית בשם species שמזהה את 36 מיני העצים ביער מסוים. בנוסף, נניח שכל דוגמה מזהה רק מין אחד.

אפשר להשתמש בווקטור one-hot כדי לייצג את מיני העצים בכל דוגמה. וקטור one-hot יכיל ערך 1 אחד (לייצוג של מין העץ הספציפי בדוגמה) ו-35 ערכים של 0 (לייצוג של 35 מיני העצים שלא בדוגמה). לכן, ייצוג one-hot של maple יכול להיראות כך:

לחלופין, ייצוג דליל יזהה פשוט את המיקום של המינים הספציפיים. אם maple נמצא במיקום 24, הייצוג הדליל של maple יהיה פשוט:

24

שימו לב שהייצוג הדליל הרבה יותר קומפקטי מהייצוג one-hot.

הערה: לא מומלץ להעביר ייצוג דליל כקלט תכונה ישיר למודל. במקום זאת, צריך להמיר את הייצוג הדליל לייצוג one-hot לפני שמבצעים אימון על בסיסו.

כדי לראות דוגמה קצת יותר מורכבת, לוחצים על הסמל.

נניח שכל דוגמה במודל צריכה לייצג את המילים – אבל לא את הסדר שלהן – במשפט באנגלית. האנגלית כוללת כ-170,000 מילים, ולכן היא מאפיין קטגורי עם כ-170,000 רכיבים. רוב המשפטים באנגלית משתמשים בחלק קטן מאוד מ-170,000 המילים האלה, ולכן קבוצת המילים בדוגמה בודדת כמעט תמיד תהיה נתונים דלילים.

נניח שיש לכם את המשפט הבא:

My dog is a great dog

אפשר להשתמש בווקטור one-hot כדי לייצג את המילים במשפט הזה. בגרסה הזו, כמה תאים בווקטור יכולים להכיל ערך שונה מאפס. בנוסף, בגרסה הזו, תא יכול להכיל מספר שלם שאינו אחד. המילים my, is, a ו-great מופיעות רק פעם אחת במשפט, אבל המילה dog מופיעה פעמיים. שימוש בווריאציה הזו של וקטורים עם קידוד one-hot כדי לייצג את המילים במשפט הזה יוצר את הווקטור הבא עם 170,000 רכיבים:

ייצוג דליל של אותו משפט יהיה פשוט:

0: 1
26100: 2
45770: 1
58906: 1
91520: 1

---

אם אתם לא מבינים משהו, לוחצים על הסמל.

המונח 'ייצוג דליל' מבלבל הרבה אנשים כי ייצוג דליל הוא לא וקטור דליל. במקום זאת, ייצוג דליל הוא למעשה ייצוג צפוף של וקטור דליל. המילה הנרדפת ייצוג אינדקס קצת יותר ברורה מהמונח 'ייצוג דליל'.

---

מידע נוסף זמין במאמר עבודה עם נתונים שמחולקים לקטגוריות בסדנה ללימוד מכונת למידה.

וקטור דליל

#fundamentals

וקטור שהערכים שלו הם בעיקר אפסים. כדאי לעיין גם בתכונת הדלילות ובדלילות.

squared loss

#fundamentals

#Metric

מילה נרדפת לירידה ברמת _L2.

סטטי

#fundamentals

משהו שעושים פעם אחת ולא באופן רציף. המונחים סטטי ואופליין הם מילים נרדפות. אלה שימושים נפוצים במונחים סטטי ואופליין בלמידת מכונה:

• מודל סטטי (או מודל אופליין) הוא מודל שעובר אימון פעם אחת ואז משתמשים בו למשך תקופה.
• אימון סטטי (או אימון אופליין) הוא תהליך האימון של מודל סטטי.
• היקש סטטי (או היקש אופליין) הוא תהליך שבו מודל יוצר קבוצה של תחזיות בכל פעם.

ניגודיות לדינמי.

היקש סטטי

#fundamentals

מילה נרדפת להסקת מסקנות במצב אופליין.

סטציונריות

#fundamentals

תכונה שהערכים שלה לא משתנים לאורך מאפיין אחד או יותר, בדרך כלל זמן. לדוגמה, תכונה שהערכים שלה דומים ב-2021 וב-2023 מציגה סטציונריות.

בעולם האמיתי, מעט מאוד תכונות מציגות סטציונריות. גם תכונות שמזוהות עם יציבות (כמו גובה פני הים) משתנות עם הזמן.

ההפך מאי-סטציונריות.

ירידת גרדיאנט סטוכסטית (SGD)

#fundamentals

אלגוריתם gradient descent שבו גודל האצווה הוא אחד. במילים אחרות, SGD מתאמן על דוגמה אחת שנבחרה באופן אחיד ואקראי מתוך קבוצת אימון.

מידע נוסף זמין במאמר רגרסיה ליניארית: היפר-פרמטרים בקורס המקוצר על למידת מכונה.

למידת מכונה מפוקחת

#fundamentals

אימון מודל מתכונות ותוויות תואמות. למידת מכונה מפוקחת דומה ללימוד נושא מסוים על ידי עיון בסדרת שאלות ובתשובות המתאימות להן. אחרי שהתלמיד או התלמידה מבינים את הקשר בין השאלות לתשובות, הם יכולים לענות על שאלות חדשות (שלא נראו קודם) באותו נושא.

השוואה ללמידת מכונה לא מפוקחת.

מידע נוסף זמין במאמר Supervised Learning (למידה מפוקחת) בקורס Introduction to ML (מבוא ל-ML).

תכונה סינתטית

#fundamentals

תכונה שלא מופיעה בין תכונות הקלט, אבל מורכבת מאחת או יותר מהן. שיטות ליצירת תכונות סינתטיות:

• חלוקה לקטגוריות של תכונה רציפה לקטגוריות של טווחים.
• יצירת תכונה חוצה.
• הכפלה (או חלוקה) של ערך תכונה אחד בערך תכונה אחר או בכמה ערכים אחרים, או בעצמו. לדוגמה, אם a ו-b הם מאפייני קלט, אלה דוגמאות למאפיינים סינתטיים:
  • ab
  • a²
• החלת פונקציה טרנסצנדנטית על ערך של תכונה. לדוגמה, אם c הוא מאפיין קלט, אלה דוגמאות למאפיינים סינתטיים:
  • sin(c)
  • ln(c)

תכונות שנוצרו על ידי נרמול או שינוי קנה מידה בלבד לא נחשבות לתכונות סינתטיות.

T

אובדן נתונים במהלך בדיקה

#fundamentals

#Metric

מדד שמייצג את הפסד של מודל בהשוואה לקבוצת הבדיקה. כשבונים מודל, בדרך כלל מנסים למזער את הפסד הבדיקה. הסיבה לכך היא שערך נמוך של הפסד בבדיקה הוא אות איכות חזק יותר מערך נמוך של הפסד באימון או ערך נמוך של הפסד באימות.

פער גדול בין הפסד הבדיקה לבין הפסד האימון או הפסד האימות מצביע לפעמים על הצורך להגדיל את שיעור הרגולריזציה.

הדרכה

#fundamentals

התהליך של קביעת הפרמטרים האידיאליים (משקלים והטיות) שמרכיבים מודל. במהלך האימון, המערכת קוראת דוגמאות ומתאימה בהדרגה את הפרמטרים. במהלך האימון, כל דוגמה משמשת בין כמה פעמים למיליארדי פעמים.

מידע נוסף זמין במאמר Supervised Learning (למידה מפוקחת) בקורס Introduction to ML (מבוא ל-ML).

הפסד האימון

#fundamentals

#Metric

מדד שמייצג את האובדן של מודל במהלך איטרציה מסוימת של אימון. לדוגמה, נניח שפונקציית ההפסד היא Mean Squared Error. יכול להיות שההפסד של האימון (השגיאה הממוצעת בריבוע) באיטרציה העשירית הוא 2.2, וההפסד של האימון באיטרציה ה-100 הוא 1.9.

בעקומת הפסד מוצג הפסד האימון לעומת מספר האיטרציות. עקומת ההפסד מספקת את הרמזים הבאים לגבי האימון:

• שיפוע כלפי מטה מעיד על שיפור במודל.
• שיפוע כלפי מעלה מעיד על כך שהמודל הולך ומשתפר.
• שיפוע שטוח מרמז שהמודל הגיע להתכנסות.

לדוגמה, בעקומת ההפסד הבאה, שהיא מעט אידיאלית, מוצגים:

• שיפוע חד כלפי מטה במהלך האיטרציות הראשוניות, שמצביע על שיפור מהיר במודל.
• שיפוע שמשתטח בהדרגה (אבל עדיין יורד) עד לסיום האימון, מה שמצביע על שיפור מתמשך של המודל בקצב איטי יותר מאשר במהלך האיטרציות הראשוניות.
• שיפוע מתון לקראת סוף האימון, שמצביע על התכנסות.

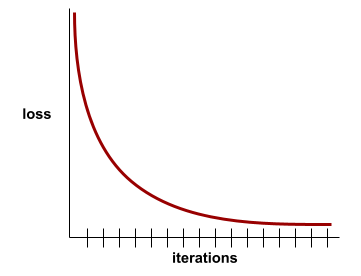
למרות שחשוב להבין את הפסדי האימון, כדאי גם לעיין במושג הכללה.

training-serving skew

#fundamentals

ההבדל בין הביצועים של מודל במהלך האימון לבין הביצועים של אותו מודל במהלך הצגת המודל.

קבוצת נתונים לאימון

#fundamentals

קבוצת המשנה של מערך הנתונים שמשמשת לאימון מודל.

באופן מסורתי, הדוגמאות במערך הנתונים מחולקות לשלוש קבוצות משנה נפרדות:

• קבוצת נתונים לאימון
• קבוצת נתונים לתיקוף
• קבוצת נתונים לבדיקה

באופן אידיאלי, כל דוגמה בקבוצת הנתונים צריכה להיות שייכת רק לאחת מקבוצות המשנה הקודמות. לדוגמה, דוגמה אחת לא יכולה להיות גם בקבוצת האימון וגם בקבוצת האימות.

מידע נוסף זמין במאמר מערכי נתונים: חלוקת מערך הנתונים המקורי בקורס המקוצר על למידת מכונה.

שלילי אמיתי (TN)

#fundamentals

#Metric

דוגמה שבה המודל מנבא בצורה נכונה את הסיווג השלילי. לדוגמה, המודל מסיק שהודעת אימייל מסוימת היא לא ספאם, והודעת האימייל הזו באמת לא ספאם.

חיובי אמיתי (TP)

#fundamentals

#Metric

דוגמה שבה המודל מנבא בצורה נכונה את הסיווג החיובי. לדוגמה, המודל מסיק שהודעת אימייל מסוימת היא ספאם, והודעת האימייל הזו באמת ספאם.

שיעור החיוביים האמיתיים (TPR)

#fundamentals

#Metric

מילה נרדפת לrecall. כלומר:

$$\text{true positive rate} = \frac {\text{true positives}} {\text{true positives} + \text{false negatives}}$$

שיעור החיוביים האמיתיים הוא ציר ה-y בעקומת ROC.

U

התאמה חסרה (underfitting)

#fundamentals

יצירת מודל עם יכולת חיזוי נמוכה, כי המודל לא הצליח לתפוס באופן מלא את המורכבות של נתוני האימון. יש הרבה בעיות שיכולות לגרום להתאמה חסרה, כולל:

• אימון על קבוצה שגויה של תכונות.
• אימון למספר נמוך מדי של תקופות אימון או בקצב למידה נמוך מדי.
• אימון עם שיעור רגולריזציה גבוה מדי.
• הוספה של מעט מדי שכבות נסתרות ברשת נוירונים עמוקה.

מידע נוסף מופיע במאמר בנושא התאמת יתר בקורס המקוצר על למידת מכונה.

דוגמה ללא תווית

#fundamentals

דוגמה שכוללת תכונות אבל לא תווית. לדוגמה, בטבלה הבאה מוצגות שלוש דוגמאות לא מסומנות ממודל להערכת שווי של בית. לכל דוגמה יש שלושה מאפיינים, אבל לא מצוין ערך הבית:

מספר חדרי שינה	מספר חדרי אמבטיה	גיל הבית
3	2	15
2	1	72
4	2	34

בלמידת מכונה מבוקרת, מודלים מתאמנים על דוגמאות מתויגות ומבצעים חיזויים על דוגמאות לא מתויגות.

בלמידה מונחית למחצה ובלמידה לא מונחית, נעשה שימוש בדוגמאות לא מסומנות במהלך האימון.

השוו בין דוגמה ללא תוויות לבין דוגמה עם תוויות.

למידת מכונה לא מפוקחת

#clustering

#fundamentals

אימון מודל כדי לזהות דפוסים במערך נתונים, בדרך כלל מערך נתונים לא מסומן.

השימוש הנפוץ ביותר בלמידת מכונה לא מפוקחת הוא אשכול של נתונים לקבוצות של דוגמאות דומות. לדוגמה, אלגוריתם ללמידת מכונה לא מפוקחת יכול לקבץ שירים לאשכולות על סמך מאפיינים שונים של המוזיקה. האשכולות שמתקבלים יכולים לשמש כקלט לאלגוריתמים אחרים של למידת מכונה (למשל, לשירות המלצות למוזיקה). האשכולות יכולים לעזור אם יש מעט תוויות שימושיות או אם אין כאלה בכלל. לדוגמה, בתחומים כמו מניעת ניצול לרעה והונאה, אשכולות יכולים לעזור לבני אדם להבין טוב יותר את הנתונים.

ההבדל בין למידת מכונה לא מפוקחת לבין למידת מכונה מפוקחת.

כדי לראות הערות נוספות, לוחצים על הסמל.

דוגמה נוספת ללמידת מכונה לא מפוקחת היא ניתוח רכיבים עיקריים (PCA). לדוגמה, יישום PCA על מערך נתונים שמכיל את התוכן של מיליוני עגלות קניות עשוי לחשוף שעגלות קניות שמכילות לימונים מכילות גם תרופות נגד צרבת.

---

מידע נוסף זמין במאמר מהי למידת מכונה? בקורס 'מבוא ל-ML'.

V

אימות

#fundamentals

הערכה ראשונית של איכות המודל. במהלך האימות נבדקת האיכות של התחזיות של המודל בהשוואה לקבוצת האימות.

מכיוון שקבוצת האימות שונה מקבוצת האימון, האימות עוזר למנוע התאמת יתר.

אפשר לחשוב על הערכת המודל ביחס לקבוצת האימות כסיבוב הראשון של הבדיקה, ועל הערכת המודל ביחס לקבוצת הבדיקה כסיבוב השני של הבדיקה.

הפסד אימות

#fundamentals

#Metric

מדד שמייצג את הפסד המודל בקבוצת האימות במהלך איטרציה מסוימת של האימון.

אפשר לעיין גם בעקומת הכללה.

קבוצת נתונים לתיקוף

#fundamentals

קבוצת המשנה של מערך הנתונים שמשמשת לביצוע הערכה ראשונית של מודל שאומן. בדרך כלל, מעריכים את המודל שאומן ביחס למערך האימות כמה פעמים לפני שמעריכים את המודל ביחס למערך הבדיקה.

באופן מסורתי, מחלקים את הדוגמאות במערך הנתונים לשלושה תת-קבוצות נפרדות:

• קבוצת נתונים לאימון
• קבוצת נתונים לתיקוף
• קבוצת נתונים לבדיקה

באופן אידיאלי, כל דוגמה בקבוצת הנתונים צריכה להיות שייכת רק לאחת מקבוצות המשנה הקודמות. לדוגמה, דוגמה אחת לא יכולה להיות גם בקבוצת האימון וגם בקבוצת האימות.

מידע נוסף זמין במאמר מערכי נתונים: חלוקת מערך הנתונים המקורי בקורס המקוצר על למידת מכונה.

W

משקל

#fundamentals

ערך שהמודל מכפיל בערך אחר. אימון הוא התהליך של קביעת המשקלים האידיאליים של המודל. הסקת מסקנות היא התהליך של שימוש במשקלים שנלמדו כדי ליצור תחזיות.

כדי לראות דוגמה למשקלים במודל ליניארי, לוחצים על הסמל.

דמיינו מודל לינארי עם שתי תכונות. נניח שהאימון קובע את המשקלים הבאים (והטיה):

• ההטיה, b, היא 2.2
• המשקל, w₁ שמשויך לתכונה אחת הוא 1.5.
• המשקל, w₂ שמשויך לתכונה השנייה הוא 0.4.

עכשיו נדמיין דוגמה עם ערכי התכונות הבאים:

• הערך של תכונה אחת, x₁, הוא 6.
• הערך של התכונה השנייה, x₂, הוא 10.

המודל הליניארי הזה משתמש בנוסחה הבאה כדי ליצור תחזית, y':

$$y' = b + w_1x_1 + w_2x_2$$

לכן, התחזית היא:

$$y' = 2.2 + (1.5)(6) + (0.4)(10) = 15.2$$

אם המשקל הוא 0, התכונה המתאימה לא תורמת למודל. לדוגמה, אם w₁ הוא 0, אז הערך של x₁ לא רלוונטי.

---

מידע נוסף זמין במאמר בנושא רגרסיה לינארית בקורס המקוצר על למידת מכונה.

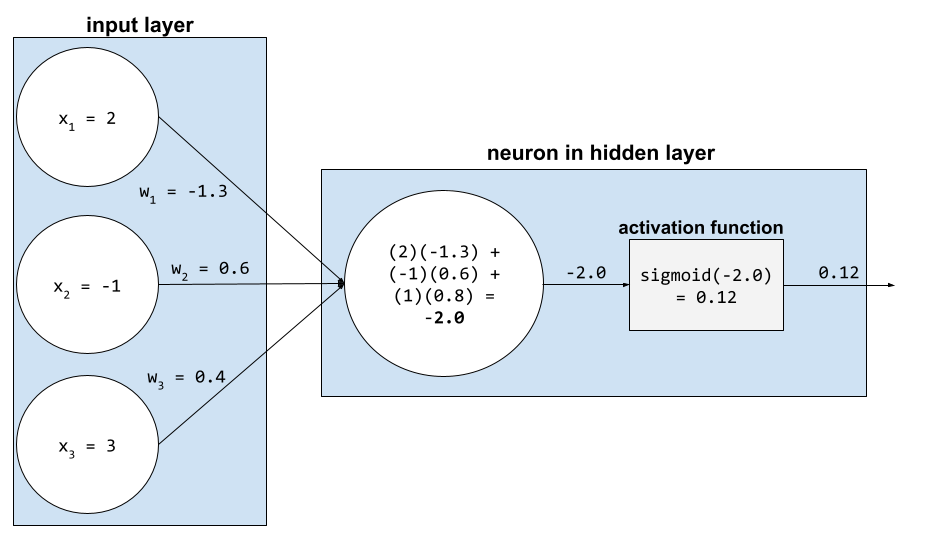
סכום משוקלל

#fundamentals

הסכום של כל ערכי הקלט הרלוונטיים כפול המשקלים המתאימים שלהם. לדוגמה, נניח שהקלט הרלוונטי כולל את הרכיבים הבאים:

ערך קלט	משקל קלט
2	‫1.3-
-1	0.6
3	0.4

לכן הסכום המשוקלל הוא:

weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0

סכום משוקלל הוא ארגומנט הקלט של פונקציית הפעלה.

Z

נורמליזציה של ציון תקן

#fundamentals

טכניקת קנה מידה שמחליפה ערך גולמי של מאפיין בערך נקודה צפה שמייצג את מספר סטיות התקן מהממוצע של המאפיין הזה. לדוגמה, נניח שיש תכונה שהממוצע שלה הוא 800 וסטיית התקן שלה היא 100. בטבלה הבאה מוצגת דוגמה למיפוי של ערך גולמי לציון Z שלו באמצעות נורמליזציה של ציון Z:

ערך גולמי	ציון תקן
800	0
950	‫+1.5
575	‫‎-2.25

לאחר מכן, המודל של למידת המכונה מתאמן על ציוני ה-Z של התכונה הזו במקום על הערכים הגולמיים.

מידע נוסף זמין במאמר נתונים מספריים: נורמליזציה בסדנה ללימוד מכונת למידה.