בתרגיל הקודם ראינו שרק הוספת שכבות סמויות לרשת לא מספיקה כדי לייצג פונקציות לא לינאריות. פעולות ליניאריות המבוצעות בפעולות ליניאריות הן עדיין ליניאריות.
איך אפשר להגדיר רשת נוירונים כדי ללמוד על קשרים לא לינאריים בין ערכים? אנחנו צריכים דרך להוסיף למודל פעולות מתמטיות לא לינאריות.
אם זה נראה קצת מוכר, הסיבה לכך היא שבאמת יישמנו פעולות מתמטיות לא ליניאריות על הפלט של מודל ליניארי מוקדם יותר במהלך הקורס. במודול Logistic Regression, התאמנו מודל של רגרסיה לינארית כדי להפיק ערך רציף מ-0 ל-1 (שמייצג הסתברות), על ידי העברת הפלט של המודל דרך פונקציית סיגמויד.
אפשר להחיל את אותו עיקרון על רשת העצבים שלנו. נבחן שוב את המודל שלנו מתרגיל 2, אבל הפעם, לפני שאנחנו נותנים את הערך של כל צומת כפלט, אנחנו מחילים קודם את פונקציית הסיגמוייד:
נסו לבצע את החישובים של כל צומת באמצעות לחיצה על הלחצן >| (משמאל ללחצן ההפעלה). אפשר לבדוק את הפעולות המתמטיות שבוצעו כדי לחשב את הערך של כל צומת בחלונית Calculations שמתחת לתרשים. שימו לב שהפלט של כל צומת הוא עכשיו טרנספורמציה סיגמואידית של השילוב הליניארי של הצמתים בשכבה הקודמת, וערכי הפלט כולם מצומצמים בין 0 ל-1.
כאן, הפונקציה הסיגמואידית משמשת כפונקציית הפעלה לרשת העצבית, טרנספורמציה לא לינארית של ערך הפלט של נוירון לפני שהערך מועבר כקלט לחישובים של השכבה הבאה ברשת העצבית.
עכשיו, אחרי שהוספנו פונקציית הפעלה, להוספת שכבות יש השפעה רבה יותר. סידור נתונים לא ליניאריים בערימה על אי-ליניאריות מאפשר לנו לבנות מודלים של קשרים מורכבים מאוד בין הקלט לפלט החזוי. בקצרה, כל שכבה לומדת בפועל פונקציה מורכבת יותר ברמה גבוהה יותר על סמך הקלט הגולמי. אם אתם רוצים לפתח יותר הבנה לגבי אופן הפעולה, כדאי לקרוא את הפוסט המעולה של כריס אולה בבלוג.
פונקציות הפעלה נפוצות
שלוש פונקציות מתמטיות שמשמשות לעיתים קרובות כפונקציות הפעלה הן sigmoid, tanh ו-ReLU.
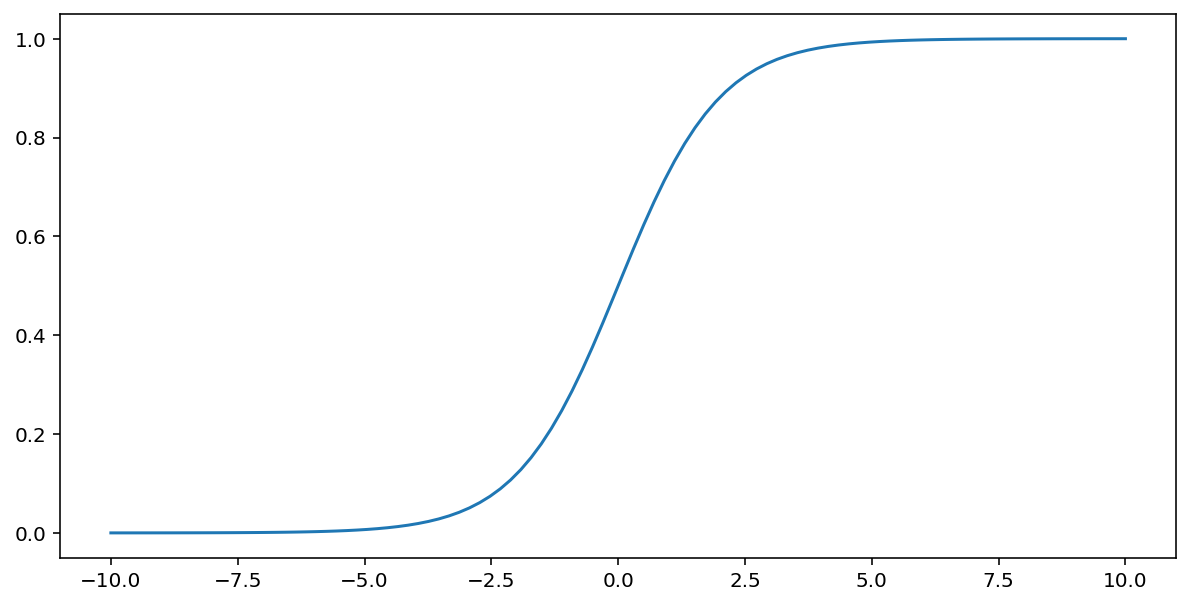
פונקציית הסיגמואיד (שנדונה למעלה) מבצעת את הטרנספורמציה הבאה על הקלט $x$, ומפיקה ערך פלט בין 0 ל-1:
\[F(x)=\frac{1} {1+e^{-x}}\]
זוהי תרשים של הפונקציה הזו:
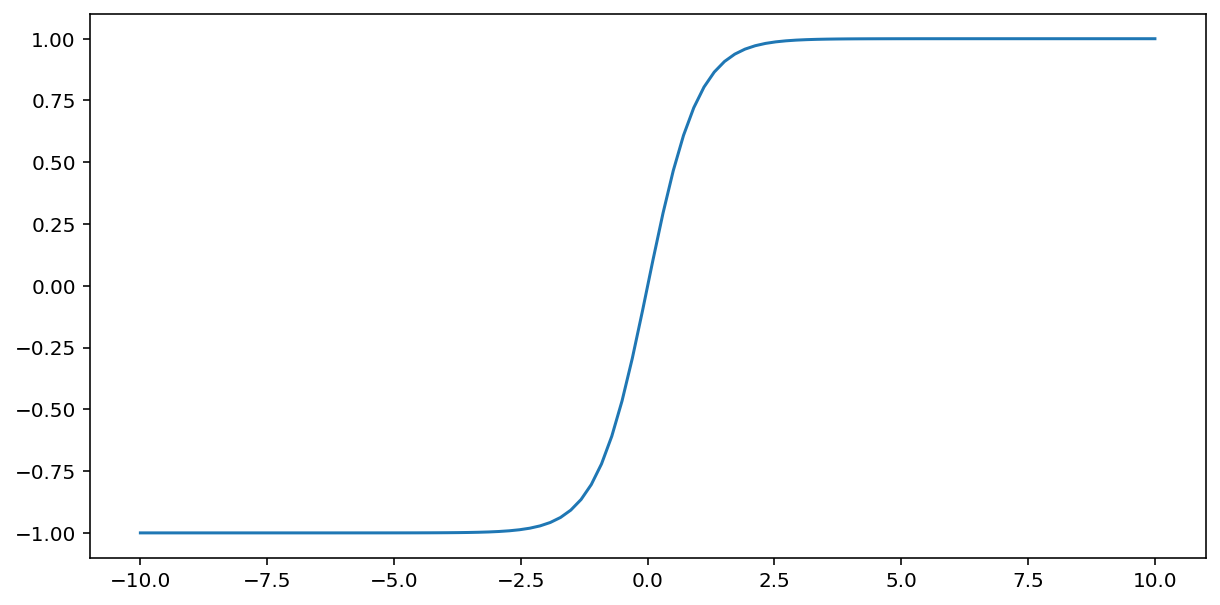
הפונקציה tanh (קיצור של 'קוטנגנס היפרבולי') הופכת את הקלט x כדי לייצר ערך פלט בין -1 ל-1:
\[F(x)=tanh(x)\]
זוהי תרשים של הפונקציה הזו:
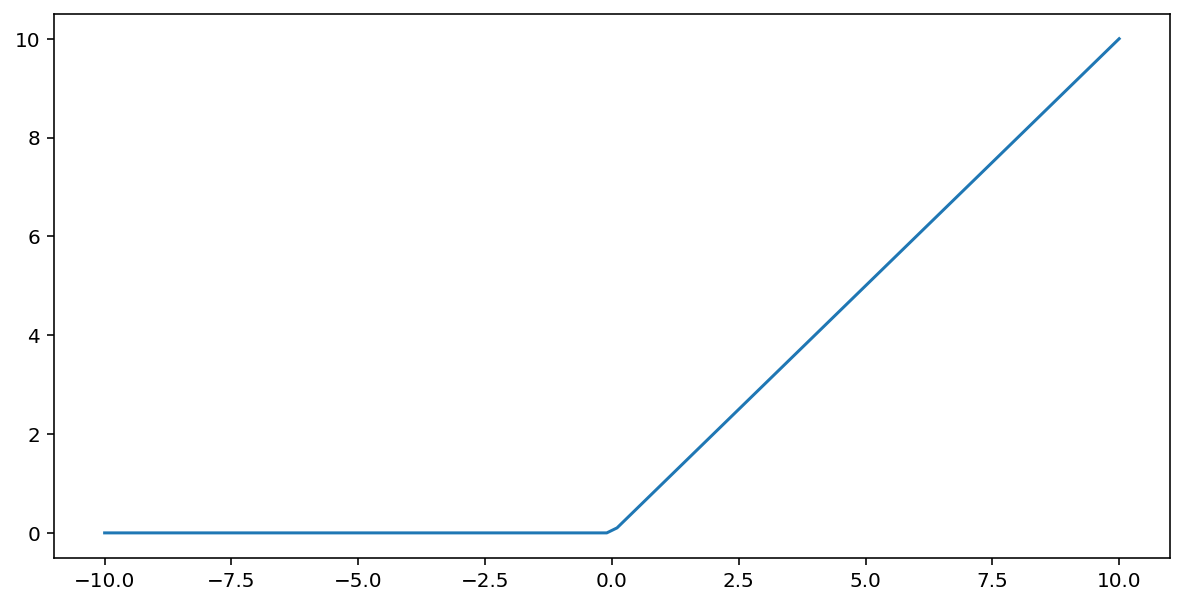
פונקציית ההפעלה של יחידה ליניארית מתוקנת (או ReLU בקיצור) מבצעת טרנספורמציה של הפלט באמצעות האלגוריתם הבא:
- אם ערך הקלט $x$ קטן מ-0, הפונקציה מחזירה 0.
- אם ערך הקלט $x$ גדול מ-0 או שווה לו, מוחזר ערך הקלט.
אפשר לייצג ReLU באופן מתמטי באמצעות הפונקציה max() :
זוהי תרשים של הפונקציה הזו:
לרוב, פונקציית ReLU פועלת טוב יותר כפונקציית הפעלה מאשר פונקציה חלקה כמו sigmoid או tanh, כי היא פחות נוטה לבעיית שיפוע נעלם במהלך אימון רשתות נוירונליות. בנוסף, קל יותר לבצע חישוב של ReLU מאשר של הפונקציות האלה.
פונקציות הפעלה אחרות
בפועל, כל פונקציה מתמטית יכולה לשמש כפונקציית הפעלה. נניח ש- \(\sigma\) מייצגת את פונקציית ההפעלה שלנו. הערך של צומת ברשת מחושב לפי הנוסחה הבאה:
Keras מספק תמיכה מובנית בפונקציות הפעלה רבות. עם זאת, עדיין מומלץ להתחיל עם ReLU.
סיכום
בסרטון הבא מופיע סיכום של כל מה שלמדתם עד עכשיו על האופן שבו נוצרות רשתות נוירונים:
עכשיו המודל שלנו כולל את כל הרכיבים הסטנדרטיים של מה שאנשים בדרך כלל מתכוונים אליו כשהם מדברים על רשת עצבית:
- קבוצה של צמתים, בדומה לנוירונים, שמאורגנים בשכבות.
- קבוצת משקלים שמייצגת את החיבורים בין כל שכבה ברשת העצבית לבין השכבה שמתחתיה. השכבה שמתחת עשויה להיות שכבת רשת נוירונים אחרת או שכבה מסוג אחר.
- קבוצה של הטיות, אחת לכל צומת.
- פונקציית הפעלה שממירה את הפלט של כל צומת בשכבה. לשכבות שונות יכולות להיות פונקציות הפעלה שונות.
הערה: רשתות נוירונים לא תמיד טובות יותר ממיזוג תכונות, אבל הן מציעות חלופה גמישה שפועלת היטב במקרים רבים.
