Glossaire du machine learning: Bases du ML

Cette page contient les termes du glossaire des principes fondamentaux du ML. Pour consulter tous les termes du glossaire, cliquez ici.

A

accuracy

#fundamentals

#Metric

Nombre de prédictions de classification correctes divisé par le nombre total de prédictions. Par exemple :

$$\text{Accuracy} = \frac{\text{correct predictions}} {\text{correct predictions + incorrect predictions }}$$

Par exemple, un modèle qui a fait 40 prédictions correctes et 10 prédictions incorrectes aurait une précision de :

$$\text{Accuracy} = \frac{\text{40}} {\text{40 + 10}} = \text{80%}$$

La classification binaire fournit des noms spécifiques pour les différentes catégories de prédictions correctes et de prédictions incorrectes. La formule de précision pour la classification binaire est la suivante :

$$\text{Accuracy} = \frac{\text{TP} + \text{TN}} {\text{TP} + \text{TN} + \text{FP} + \text{FN}}$$

où :

• TP correspond au nombre de vrais positifs (prédictions correctes).
• TN correspond au nombre de vrais négatifs (prédictions correctes).
• FP correspond au nombre de faux positifs (prédictions incorrectes).
• FN correspond au nombre de faux négatifs (prédictions incorrectes).

Comparer et opposer la justesse à la précision et au rappel.

Cliquez sur l'icône pour en savoir plus sur la précision et les ensembles de données déséquilibrés.

Bien qu'il s'agisse d'une métrique utile dans certaines situations, la précision est très trompeuse dans d'autres. En particulier, la précision est généralement une mauvaise métrique pour évaluer les modèles de classification qui traitent les ensembles de données déséquilibrés en termes de classes.

Par exemple, supposons qu'il ne neige que 25 jours par siècle dans une certaine ville subtropicale. Comme les jours sans neige (classe négative) sont beaucoup plus nombreux que les jours avec neige (classe positive), l'ensemble de données sur la neige pour cette ville est déséquilibré. Imaginez un modèle de classification binaire qui est censé prédire s'il va neiger ou non chaque jour, mais qui prédit simplement "pas de neige" tous les jours. Ce modèle est très précis, mais n'a aucun pouvoir prédictif. Le tableau suivant récapitule les résultats pour un siècle de prédictions :

Catégorie	Nombre
VP	0
TN	36499
FP	0
FN	25

La précision de ce modèle est donc la suivante :

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (0 + 36499) / (0 + 36499 + 0 + 25) = 0.9993 = 99.93%

Bien qu'une précision de 99,93 % semble très impressionnante, le modèle n'a en réalité aucun pouvoir prédictif.

La précision et le rappel sont généralement des métriques plus utiles que la justesse pour évaluer les modèles entraînés sur des ensembles de données aux classes déséquilibrées.

---

Pour en savoir plus, consultez Classification : précision, rappel, exactitude et métriques associées dans le Cours d'initiation au Machine Learning.

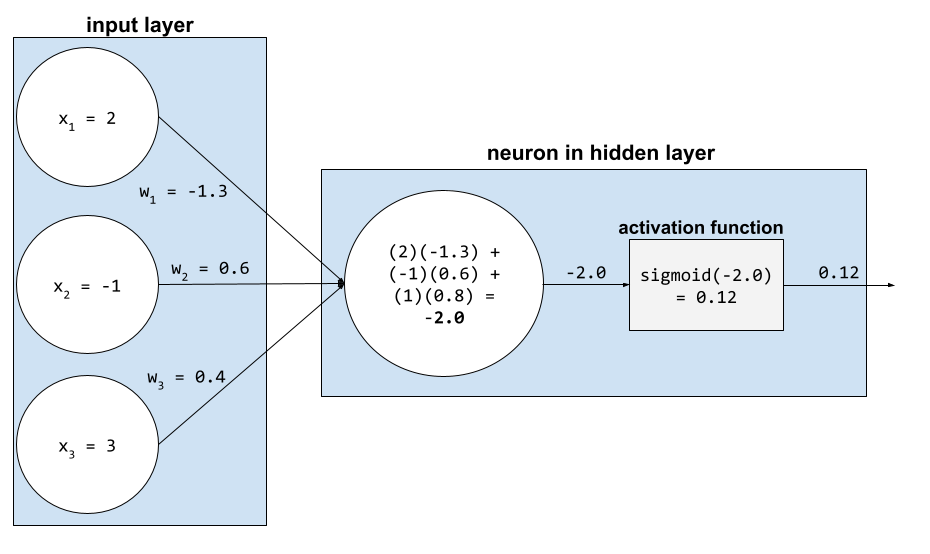
fonction d'activation

#fundamentals

Fonction qui permet aux réseaux de neurones d'apprendre les relations non linéaires (complexes) entre les caractéristiques et le libellé.

Voici quelques fonctions d'activation courantes :

• ReLU
• Sigmoïde

Les graphiques des fonctions d'activation ne sont jamais des lignes droites. Par exemple, le graphique de la fonction d'activation ReLU se compose de deux lignes droites :

Voici à quoi ressemble un graphique de la fonction d'activation sigmoïde :

Cliquez sur l'icône pour voir un exemple.

Dans un réseau de neurones, les fonctions d'activation manipulent la somme pondérée de toutes les entrées d'un neurone. Pour calculer une somme pondérée, le neurone additionne les produits des valeurs et des pondérations concernées. Par exemple, supposons que l'entrée pertinente d'un neurone se compose des éléments suivants :

valeur d'entrée	pondération d'entrée
2	-1,3
-1	0,6
3	0,4

La somme pondérée est donc la suivante :

weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0

Supposons que le concepteur de ce réseau de neurones choisisse la fonction sigmoïde comme fonction d'activation. Dans ce cas, le neurone calcule le sigmoïde de -2,0, qui est d'environ 0,12. Le neurone transmet donc 0,12 (plutôt que -2,0) à la couche suivante du réseau de neurones. La figure suivante illustre la partie concernée du processus :

---

Pour en savoir plus, consultez Réseaux de neurones : fonctions d'activation dans le Cours d'initiation au Machine Learning.

intelligence artificielle

#fundamentals

Un programme ou un modèle non humain capable de résoudre des tâches complexes. Par exemple, un programme ou un modèle qui traduit du texte ou un programme ou un modèle qui identifie des maladies à partir d'images radiologiques font tous deux preuve d'intelligence artificielle.

Formellement, le machine learning est un sous-domaine de l'intelligence artificielle. Toutefois, ces dernières années, certaines organisations ont commencé à utiliser les termes intelligence artificielle et machine learning de manière interchangeable.

AUC (aire sous la courbe ROC)

#fundamentals

#Metric

Nombre compris entre 0,0 et 1,0 représentant la capacité d'un modèle de classification binaire à séparer les classes positives des classes négatives. Plus l'AUC est proche de 1,0, plus le modèle est performant pour séparer les classes les unes des autres.

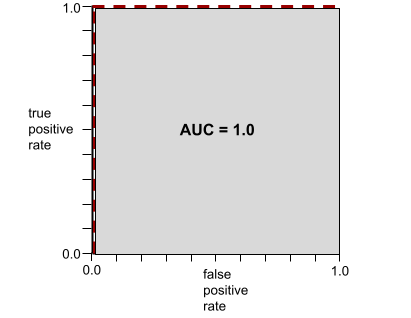
Par exemple, l'illustration suivante montre un modèle de classification qui sépare parfaitement les classes positives (ovales verts) des classes négatives (rectangles violets). Ce modèle parfait et irréaliste a une AUC de 1,0 :

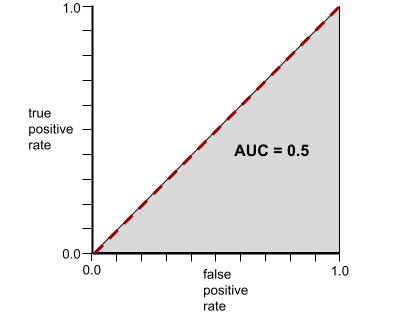
À l'inverse, l'illustration suivante montre les résultats d'un modèle de classification qui a généré des résultats aléatoires. Ce modèle a une AUC de 0,5 :

Oui, le modèle précédent a une AUC de 0,5, et non de 0.

La plupart des modèles se situent entre ces deux extrêmes. Par exemple, le modèle suivant sépare plus ou moins les positifs des négatifs et présente donc une AUC comprise entre 0,5 et 1,0 :

L'AUC ignore toute valeur que vous définissez pour classification threshold. L'AUC prend en compte tous les seuils de classification possibles.

Cliquez sur l'icône pour en savoir plus sur la relation entre les courbes AUC et ROC.

L'AUC représente l'aire sous une courbe ROC. Par exemple, la courbe ROC d'un modèle qui sépare parfaitement les positifs des négatifs se présente comme suit :

L'AUC correspond à la zone grise de l'illustration précédente. Dans ce cas inhabituel, la surface correspond simplement à la longueur de la région grise (1,0) multipliée par sa largeur (1,0). Ainsi, le produit de 1,0 et 1,0 donne une AUC de exactement 1,0, qui est le score AUC le plus élevé possible.

À l'inverse, la courbe ROC d'un modèle de classification qui ne peut pas du tout séparer les classes est la suivante. L'aire de cette région grise est de 0,5.

Une courbe ROC plus typique ressemble approximativement à ce qui suit :

Il serait fastidieux de calculer manuellement l'aire sous cette courbe. C'est pourquoi un programme calcule généralement la plupart des valeurs AUC.

---

Cliquez sur l'icône pour obtenir une définition plus formelle de l'AUC.

L'AUC correspond à la probabilité qu'un modèle de classification soit plus confiant qu'un exemple positif choisi aléatoirement soit effectivement positif par rapport à un exemple négatif choisi aléatoirement.

---

Pour en savoir plus, consultez Classification : ROC et AUC dans le Cours d'initiation au machine learning.

B

rétropropagation

#fundamentals

Algorithme qui implémente la descente de gradient dans les réseaux de neurones.

L'entraînement d'un réseau de neurones implique de nombreuses itérations du cycle à deux passes suivant :

1. Lors de la propagation directe, le système traite un lot d'exemples pour générer une ou plusieurs prédictions. Le système compare chaque prédiction à chaque valeur de libellé. La différence entre la prédiction et la valeur de l'étiquette correspond à la perte pour cet exemple. Le système agrège les pertes de tous les exemples pour calculer la perte totale du lot actuel.
2. Lors de la propagation à rebours (rétropropagation), le système réduit la perte en ajustant les pondérations de tous les neurones dans toutes les couches cachées.

Les réseaux de neurones contiennent souvent de nombreux neurones répartis sur plusieurs couches cachées. Chacun de ces neurones contribue à la perte globale de différentes manières. La rétropropagation détermine s'il faut augmenter ou diminuer les pondérations appliquées à certains neurones.

Le taux d'apprentissage est un multiplicateur qui contrôle le degré d'augmentation ou de diminution de chaque poids à chaque passe arrière. Un taux d'apprentissage élevé augmentera ou diminuera chaque poids plus qu'un taux d'apprentissage faible.

En termes de calcul, la rétropropagation implémente la règle de la chaîne du calcul. Autrement dit, la rétropropagation calcule la dérivée partielle de l'erreur par rapport à chaque paramètre.

Il y a quelques années, les spécialistes du ML devaient écrire du code pour implémenter la rétropropagation. Les API de ML modernes comme Keras implémentent désormais la rétropropagation pour vous. Ouf !

Pour en savoir plus, consultez la section Réseaux de neurones du cours d'initiation au machine learning.

lot

#fundamentals

Ensemble d'exemples utilisés dans une itération d'entraînement. La taille de lot détermine le nombre d'exemples dans un lot.

Pour comprendre le lien entre un lot et une époque, consultez époque.

Pour en savoir plus, consultez Régression linéaire : hyperparamètres dans le Cours d'initiation au Machine Learning.

taille du lot

#fundamentals

Nombre d'exemples dans un lot. Par exemple, si la taille de lot est de 100, le modèle traite 100 exemples par itération.

Voici quelques stratégies de taille de lot populaires :

• Descente de gradient stochastique (SGD, Stochastic Gradient Descent), dans laquelle la taille de lot est égale à 1.
• Lot complet : la taille du lot correspond au nombre d'exemples dans l'ensemble d'entraînement. Par exemple, si l'ensemble d'entraînement contient un million d'exemples, la taille du lot sera d'un million d'exemples. Le traitement par lot complet est généralement une stratégie inefficace.
• Mini-lot, dont la taille est généralement comprise entre 10 et 1 000. Le mini-lot est généralement la stratégie la plus efficace.

Pour en savoir plus, lisez les informations ci-après.

• Systèmes de production de ML : inférence statique ou dynamique dans le cours d'initiation au machine learning
• Playbook sur l'optimisation du deep learning.

biais (éthique/équité) (bias (ethics/fairness))

#responsible

#fundamentals

1. Stéréotypes, préjudice ou favoritisme envers certains groupes, choses ou personnes par rapport à d'autres. Ces biais peuvent avoir une incidence sur la collecte et l'interprétation des données, ainsi que sur la conception d'un système et la manière dont les utilisateurs interagissent avec celui-ci. Les formes de ce type de biais comprennent les éléments suivants :

• biais d'automatisation
• biais de confirmation
• effet expérimentateur
• biais de représentativité
• biais implicite
• biais d'appartenance
• biais d'homogénéité de l'exogroupe

2. Erreur systématique introduite par une procédure d'échantillonnage ou de rapport. Les formes de ce type de biais comprennent les éléments suivants :

• Biais de couverture
• biais de non-réponse
• biais de participation
• biais de fréquence
• biais d'échantillonnage
• biais de sélection

À ne pas confondre avec le biais des modèles de machine learning ou le biais de prédiction.

Pour en savoir plus, consultez Équité : types de biais dans le cours d'initiation au machine learning.

biais (mathématiques) ou terme de biais

#fundamentals

Ordonnée à l'origine ou décalage par rapport à une origine. Le biais est un paramètre des modèles de machine learning, symbolisé par l'un des éléments suivants :

• b
• w₀

Par exemple, b représente le biais dans la formule suivante :

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

Dans une ligne bidimensionnelle simple, le biais signifie simplement "ordonnée à l'origine". Par exemple, le biais de la ligne dans l'illustration suivante est de 2.

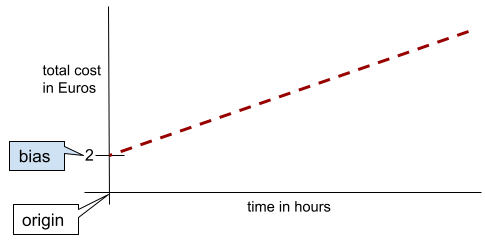
Le biais existe, car tous les modèles ne partent pas de l'origine (0,0). Par exemple, supposons qu'un parc d'attractions coûte 2 euros à l'entrée et 0,5 euro supplémentaire par heure passée par un client. Par conséquent, un modèle mappant le coût total présente un biais de 2, car le coût le plus bas est de 2 euros.

Le biais ne doit pas être confondu avec le biais en matière d'éthique et d'équité ni avec le biais de prédiction.

Pour en savoir plus, consultez Régression linéaire dans le cours d'initiation au machine learning.

classification binaire

#fundamentals

Type de tâche de classification qui prédit l'une des deux classes mutuellement exclusives :

• la classe positive
• la classe négative

Par exemple, les deux modèles de machine learning suivants effectuent chacun une classification binaire :

• Modèle qui détermine si les e-mails sont du spam (classe positive) ou non-spam (classe négative).
• Un modèle qui évalue les symptômes médicaux pour déterminer si une personne est atteinte d'une maladie spécifique (classe positive) ou non (classe négative).

À comparer à la classification à classes multiples.

Consultez également Régression logistique et Seuil de classification.

Pour en savoir plus, consultez la section Classification du cours d'initiation au machine learning.

le binning

#fundamentals

Conversion d'une seule caractéristique en plusieurs caractéristiques binaires appelées ensembles ou classes, généralement en fonction d'une plage de valeurs. La caractéristique tronquée est généralement une caractéristique continue.

Par exemple, au lieu de représenter la température comme une seule caractéristique continue à virgule flottante, vous pouvez découper les plages de températures en buckets distincts, tels que :

• La catégorie "froid" correspond à une température inférieure ou égale à 10 degrés Celsius.
• La tranche "tempérée" correspondrait à une température comprise entre 11 et 24 degrés Celsius.
• La tranche "chaud" correspondrait à une température supérieure ou égale à 25 degrés Celsius.

Le modèle traitera chaque valeur du même bucket de manière identique. Par exemple, les valeurs 13 et 22 se trouvent toutes les deux dans le bucket "tempéré". Le modèle les traite donc de manière identique.

Cliquez sur l'icône pour afficher des notes supplémentaires.

Si vous représentez la température comme une caractéristique continue, le modèle la traite comme une caractéristique unique. Si vous représentez la température sous forme de trois groupes, le modèle traite chaque groupe comme une caractéristique distincte. Autrement dit, un modèle peut apprendre des relations distinctes entre chaque bucket et le libellé. Par exemple, un modèle de régression linéaire peut apprendre des pondérations distinctes pour chaque bucket.

Augmenter le nombre de buckets complique votre modèle en augmentant le nombre de relations que votre modèle doit apprendre. Par exemple, les buckets froid, tempéré et chaud sont essentiellement trois caractéristiques distinctes sur lesquelles votre modèle peut s'entraîner. Si vous décidez d'ajouter deux autres buckets (par exemple, "froid" et "chaud"), votre modèle devra désormais s'entraîner sur cinq caractéristiques distinctes.

Comment savoir combien de buckets créer ou quelles doivent être les plages de chaque bucket ? Les réponses nécessitent généralement pas mal d'expérimentation.

---

Pour en savoir plus, consultez Données numériques : binning dans le cours d'initiation au machine learning.

C

données catégorielles

#fundamentals

Caractéristiques avec un ensemble spécifique de valeurs possibles. Par exemple, prenons une caractéristique catégorielle nommée traffic-light-state, qui ne peut avoir que l'une des trois valeurs possibles suivantes :

• red
• yellow
• green

En représentant traffic-light-state comme une caractéristique catégorielle, un modèle peut apprendre les différents impacts de red, green et yellow sur le comportement du conducteur.

Les caractéristiques catégorielles sont parfois appelées caractéristiques discrètes.

À comparer aux données numériques.

Pour en savoir plus, consultez Utiliser des données catégorielles dans le Cours d'initiation au Machine Learning.

classe

#fundamentals

Catégorie à laquelle une étiquette peut appartenir. Exemple :

• Dans un modèle de classification binaire qui détecte le spam, les deux classes peuvent être spam et non-spam.
• Dans un modèle de classification à classes multiples qui identifie les races de chiens, les classes peuvent être caniche, beagle, carlin, etc.

Un modèle de classification prédit une classe. En revanche, un modèle de régression prédit un nombre plutôt qu'une classe.

Pour en savoir plus, consultez la section Classification du cours d'initiation au machine learning.

modèle de classification

#fundamentals

Un modèle dont la prédiction est une classe. Par exemple, les éléments suivants sont tous des modèles de classification :

• Un modèle qui prédit la langue d'une phrase saisie (français ? Espagnol ? Italien ?)
• Un modèle qui prédit les espèces d'arbres (érable ? Chêne ? Baobab ?).
• Modèle qui prédit la classe positive ou négative pour une affection médicale spécifique.

En revanche, les modèles de régression prédisent des nombres plutôt que des classes.

Voici deux types courants de modèles de classification :

• Classification binaire
• Classification à classes multiples

seuil de classification

#fundamentals

Dans une classification binaire, il s'agit d'un nombre compris entre 0 et 1 qui convertit la sortie brute d'un modèle de régression logistique en prédiction de la classe positive ou de la classe négative. Notez que le seuil de classification est une valeur choisie par un humain, et non par l'entraînement du modèle.

Un modèle de régression logistique génère une valeur brute comprise entre 0 et 1. Ensuite :

• Si cette valeur brute est supérieure au seuil de classification, la classe positive est prédite.
• Si cette valeur brute est inférieure au seuil de classification, la classe négative est prédite.

Par exemple, supposons que le seuil de classification soit de 0,8. Si la valeur brute est de 0,9, le modèle prédit la classe positive. Si la valeur brute est de 0,7, le modèle prédit la classe négative.

Le choix du seuil de classification a une forte influence sur le nombre de faux positifs et de faux négatifs.

Cliquez sur l'icône pour afficher des notes supplémentaires.

À mesure que les modèles ou les ensembles de données évoluent, les ingénieurs modifient parfois également le seuil de classification. Lorsque le seuil de classification change, les prédictions de classe positive peuvent soudainement devenir des classes négatives et inversement.

Prenons l'exemple d'un modèle de prédiction des maladies par classification binaire. Supposons que lorsque le système s'exécute la première année :

• La valeur brute pour un patient donné est de 0,95.
• Le seuil de classification est de 0,94.

Le système diagnostique donc la classe positive. (Le patient halète, "Oh non ! Je suis malade !")

Un an plus tard, les valeurs peuvent se présenter comme suit :

• La valeur brute pour le même patient reste à 0,95.
• Le seuil de classification passe à 0,97.

Le système reclassifie donc ce patient dans la classe négative. ("Bonne journée ! Je ne suis pas malade.") Le même patient. Diagnostic différent.

---

Pour en savoir plus, consultez Seuils et matrice de confusion dans le Cours d'initiation au machine learning.

classificateur

#fundamentals

Terme informel désignant un modèle de classification.

ensemble de données avec déséquilibre des classes

#fundamentals

Un ensemble de données pour une classification dans lequel le nombre total d'étiquettes de chaque classe diffère de manière significative. Prenons l'exemple d'un ensemble de données de classification binaire dont les deux libellés sont répartis comme suit :

• 1 000 000 de libellés à exclure
• 10 libellés positifs

Le ratio d'étiquettes négatives par rapport aux étiquettes positives est de 100 000 pour 1. Il s'agit donc d'un ensemble de données avec déséquilibre des classes.

En revanche, l'ensemble de données suivant est équilibré par classe, car le ratio de libellés négatifs par rapport aux libellés positifs est relativement proche de 1 :

• 517 libellés négatifs
• 483 libellés positifs

Les ensembles de données multiclasses peuvent également présenter un déséquilibre des classes. Par exemple, l'ensemble de données de classification multiclasse suivant est également déséquilibré, car un libellé comporte beaucoup plus d'exemples que les deux autres :

• 1 000 000 d'étiquettes avec la classe "vert"
• 200 étiquettes avec la classe "violet"
• 350 libellés avec la classe "orange"

L'entraînement d'ensembles de données avec déséquilibre des classes peut présenter des difficultés particulières. Pour en savoir plus, consultez Ensembles de données déséquilibrés dans le Cours d'initiation au Machine Learning.

Voir aussi entropie, classe majoritaire et classe minoritaire.

écrêtage

#fundamentals

Technique de gestion des valeurs aberrantes en effectuant l'une des opérations suivantes ou les deux :

• Abaisser les valeurs de caractéristiques qui sont au-dessus d'un seuil maximal à ce seuil maximal.
• Augmenter les valeurs de caractéristiques qui sont en-dessous d'un certain seuil minimal à ce seuil minimal.

Supposons, par exemple, que moins de 0,5 % des valeurs d'une caractéristique donnée ne sont pas comprises entre 40 et 60. Dans ce cas, vous pouvez procéder comme suit :

• Borner toutes les valeurs supérieures à 60 (le seuil maximal) pour obtenir exactement 60.
• Borner toutes les valeurs inférieures à 40 (le seuil minimal) pour obtenir exactement 40.

Les valeurs aberrantes peuvent endommager les modèles et parfois entraîner un dépassement de capacité des pondérations pendant l'entraînement. Certaines valeurs aberrantes peuvent également nuire considérablement aux métriques telles que la précision. Le clipping est une technique courante pour limiter les dégâts.

Le bornement du gradient force les valeurs de gradient dans une plage désignée pendant l'entraînement.

Pour en savoir plus, consultez Données numériques : normalisation dans le Cours d'initiation au machine learning.

matrice de confusion

#fundamentals

Table NxN qui résume le nombre de prédictions correctes et incorrectes effectuées par un modèle de classification. Prenons l'exemple de la matrice de confusion suivante pour un modèle de classification binaire :

	Tumeur (prédite)	Non tumoral (prédit)
Tumeur (vérité terrain)	18 (VP)	1 (FN)
Non-Tumor (vérité terrain)	6 (FP)	452 (VN)

La matrice de confusion précédente montre les éléments suivants :

• Sur les 19 prédictions où la vérité terrain était "Tumeur", le modèle en a classé 18 correctement et 1 incorrectement.
• Sur les 458 prédictions pour lesquelles la vérité terrain était "Non-Tumor", le modèle en a classé 452 correctement et 6 incorrectement.

La matrice de confusion pour un problème de classification multiclasse peut vous aider à identifier les types d'erreurs. Prenons l'exemple de la matrice de confusion suivante pour un modèle de classification multiclasse à trois classes qui catégorise trois types d'iris différents (Virginica, Versicolor et Setosa). Lorsque la vérité terrain était "Virginica", la matrice de confusion montre que le modèle était beaucoup plus susceptible de prédire à tort "Versicolor" que "Setosa" :

	Setosa (prédit)	Versicolor (prédit)	Virginica (prédit)
Setosa (vérité terrain)	88	12	0
Versicolor (vérité terrain)	6	141	7
Virginica (vérité terrain)	2	27	109

Par exemple, une matrice de confusion peut révéler qu'un modèle entraîné à reconnaître les chiffres écrits à la main tend à prédire de façon erronée 9 à la place de 4, ou 1 au lieu de 7.

Les matrices de confusion contiennent suffisamment d'informations pour calculer diverses métriques de performances, y compris la précision et le rappel.

caractéristique continue

#fundamentals

Caractéristique à virgule flottante avec une plage infinie de valeurs possibles, comme la température ou le poids.

À comparer à la caractéristique discrète.

convergence

#fundamentals

État atteint lorsque les valeurs de perte varient très peu ou pas du tout à chaque itération. Par exemple, la courbe de perte suivante suggère une convergence à environ 700 itérations :

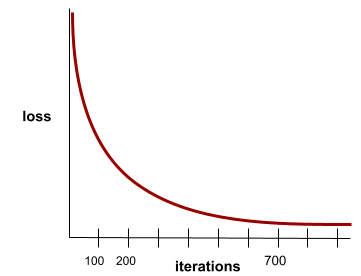
Un modèle converge lorsque la poursuite de l'entraînement ne l'améliore pas.

Dans le deep learning, les valeurs de perte restent parfois constantes ou presque pendant de nombreuses itérations avant de finalement diminuer. Pendant une longue période de valeurs de perte constantes, vous pouvez temporairement avoir une fausse impression de convergence.

Voir aussi arrêt prématuré.

Pour en savoir plus, consultez Convergence du modèle et courbes de perte dans le cours d'initiation au Machine Learning.

D

DataFrame

#fundamentals

Type de données pandas populaire pour représenter les ensembles de données en mémoire.

Un DataFrame est analogue à un tableau ou à une feuille de calcul. Chaque colonne d'un DataFrame porte un nom (un en-tête) et chaque ligne est identifiée par un numéro unique.

Chaque colonne d'un DataFrame est structurée comme un tableau à deux dimensions, sauf que chaque colonne peut se voir attribuer son propre type de données.

Consultez également la page de référence pandas.DataFrame officielle.

ensemble de données (data set ou dataset)

#fundamentals

Ensemble de données brutes, généralement (mais pas exclusivement) organisé dans l'un des formats suivants :

• une feuille de calcul
• un fichier au format CSV (valeurs séparées par une virgule)

modèle deep learning

#fundamentals

Un réseau de neurones contenant plus d'une couche cachée.

Un modèle profond est également appelé réseau de neurones profond.

À comparer au modèle large.

caractéristique dense

#fundamentals

Une feature dans laquelle la plupart ou la totalité des valeurs sont non nulles, généralement un Tensor de valeurs à virgule flottante. Par exemple, le Tensor à 10 éléments ci-dessous est dense, car 9 de ses valeurs sont non nulles :

8

3

7

5

2

4

0

4

9

6

À comparer à la caractéristique creuse.

profondeur

#fundamentals

La somme des éléments suivants dans un réseau de neurones :

• le nombre de couches cachées ;
• le nombre de couches de sortie, qui est généralement de 1.
• le nombre de couches d'embedding

Par exemple, un réseau de neurones avec cinq couches cachées et une couche de sortie a une profondeur de 6.

Notez que la couche d'entrée n'a pas d'incidence sur la profondeur.

caractéristique discrète

#fundamentals

Caractéristique avec un ensemble fini de valeurs possibles. Par exemple, une caractéristique dont les valeurs ne peuvent être que animal, végétal ou minéral est une caractéristique discrète (ou catégorielle).

À comparer à la caractéristique continue.

dynamic

#fundamentals

Quelque chose qui est fait fréquemment ou en continu. Les termes dynamique et en ligne sont synonymes dans le machine learning. Voici des utilisations courantes des termes dynamique et en ligne dans le machine learning :

• Un modèle dynamique (ou modèle en ligne) est un modèle réentraîné fréquemment ou en continu.
• L'entraînement dynamique (ou entraînement en ligne) est le processus d'entraînement fréquent ou continu.
• L'inférence dynamique (ou inférence en ligne) est le processus de génération de prédictions à la demande.

modèle dynamique

#fundamentals

Un modèle fréquemment (voire en continu) réentraîné. Un modèle dynamique est un "apprenant permanent" qui s'adapte constamment aux données en évolution. Un modèle dynamique est également appelé modèle en ligne.

À comparer au modèle statique.

E

arrêt prématuré

#fundamentals

Méthode de régularisation qui consiste à mettre fin à l'entraînement avant que la perte d'entraînement ait fini de baisser. Dans l'arrêt prématuré, vous arrêtez intentionnellement l'entraînement du modèle lorsque la perte sur un ensemble de données de validation commence à augmenter, c'est-à-dire lorsque les performances de généralisation se détériorent.

Cliquez sur l'icône pour afficher des notes supplémentaires.

L'arrêt prématuré peut sembler contre-intuitif. Après tout, dire à un modèle d'arrêter l'entraînement alors que la perte diminue encore peut sembler équivaloir à dire à un chef d'arrêter de cuisiner avant que le dessert ne soit complètement cuit. Toutefois, entraîner un modèle trop longtemps peut entraîner un surapprentissage. En d'autres termes, si vous entraînez un modèle trop longtemps, il peut s'adapter si étroitement aux données d'entraînement qu'il ne parvient pas à faire de bonnes prédictions sur de nouveaux exemples.

---

À comparer à la sortie anticipée.

couche d'embedding

#fundamentals

Une couche cachée spéciale qui s'entraîne sur une caractéristique catégorielle de grande dimension pour apprendre progressivement un vecteur d'intégration de dimension inférieure. Une couche d'intégration permet à un réseau de neurones de s'entraîner beaucoup plus efficacement que s'il s'entraînait uniquement sur la caractéristique catégorielle de grande dimension.

Par exemple, la Terre abrite actuellement environ 73 000 espèces d'arbres. Supposons que l'espèce d'arbre soit une caractéristique de votre modèle. La couche d'entrée de votre modèle inclut donc un vecteur one-hot de 73 000 éléments. Par exemple, baobab pourrait se présenter comme suit :

Un tableau de 73 000 éléments est très long. Si vous n'ajoutez pas de couche d'intégration au modèle, l'entraînement prendra beaucoup de temps en raison de la multiplication de 72 999 zéros. Vous pouvez choisir que la couche d'intégration comporte 12 dimensions. Par conséquent, la couche d'intégration apprendra progressivement un nouveau vecteur d'intégration pour chaque espèce d'arbre.

Dans certaines situations, le hachage est une alternative raisonnable à un calque d'intégration.

Pour en savoir plus, consultez Embeddings dans le Cours d'initiation au Machine Learning.

epoch

#fundamentals

Cycle d'entraînement complet sur l'intégralité de l'ensemble d'entraînement de manière à ce que chaque exemple ait été traité une fois.

Une époque représente N/taille du lot itérations d'entraînement, où N correspond au nombre total d'exemples.

Par exemple, supposons les éléments suivants :

• L'ensemble de données se compose de 1 000 exemples.
• La taille de lot est de 50 exemples.

Par conséquent, une seule époque nécessite 20 itérations :

1 epoch = (N/batch size) = (1,000 / 50) = 20 iterations

Pour en savoir plus, consultez Régression linéaire : hyperparamètres dans le Cours d'initiation au Machine Learning.

exemple

#fundamentals

Les valeurs d'une ligne de caractéristiques et éventuellement un libellé. Les exemples d'apprentissage supervisé se répartissent en deux catégories générales :

• Un exemple étiqueté se compose d'une ou plusieurs caractéristiques et d'une étiquette. Des exemples étiquetés sont utilisés pendant l'entraînement.
• Un exemple non étiqueté se compose d'une ou plusieurs caractéristiques, mais pas d'étiquette. Les exemples sans étiquette sont utilisés lors de l'inférence.

Par exemple, supposons que vous entraîniez un modèle pour déterminer l'influence des conditions météorologiques sur les résultats des élèves aux tests. Voici trois exemples annotés :

Fonctionnalités			Libellé
Température	Humidité	Pression	Note du test
15	47	998	Bonne
19	34	1020	Excellente
18	92	1012	Médiocre

Voici trois exemples non étiquetés :

Température	Humidité	Pression
12	62	1014
21	47	1017
19	41	1021

La ligne d'un ensemble de données est généralement la source brute d'un exemple. Autrement dit, un exemple se compose généralement d'un sous-ensemble des colonnes de l'ensemble de données. De plus, les caractéristiques d'un exemple peuvent également inclure des caractéristiques synthétiques, telles que des caractéristiques croisées.

Pour en savoir plus, consultez Apprentissage supervisé dans le cours "Introduction au machine learning".

F

Faux négatif (FN)

#fundamentals

#Metric

Exemple dans lequel le modèle a prédit à tort la classe négative. Par exemple, le modèle prédit qu'un e-mail particulier n'est pas du spam (classe négative), alors qu'en réalité, il l'est.

Faux positif (FP)

#fundamentals

#Metric

Exemple dans lequel le modèle prédit à tort la classe positive. Par exemple, le modèle prédit qu'un e-mail particulier est du spam (classe positive), alors qu'en réalité ce n'est pas un courrier indésirable.

Pour en savoir plus, consultez Seuils et matrice de confusion dans le Cours d'initiation au machine learning.

taux de faux positifs (TFP) (false positive rate (FPR))

#fundamentals

#Metric

Proportion d'exemples négatifs réels pour lesquels le modèle a prédit à tort la classe positive. La formule suivante permet de calculer le taux de faux positifs :

$$\text{false positive rate} = \frac{\text{false positives}}{\text{false positives} + \text{true negatives}}$$

Le taux de faux positifs correspond à l'abscisse d'une courbe ROC.

Pour en savoir plus, consultez Classification : ROC et AUC dans le Cours d'initiation au machine learning.

fonctionnalité

#fundamentals

Variable d'entrée d'un modèle de machine learning. Un exemple se compose d'une ou de plusieurs caractéristiques. Par exemple, supposons que vous entraîniez un modèle pour déterminer l'influence des conditions météorologiques sur les résultats des élèves aux tests. Le tableau suivant présente trois exemples, chacun contenant trois caractéristiques et un libellé :

Fonctionnalités			Libellé
Température	Humidité	Pression	Note du test
15	47	998	92
19	34	1020	84
18	92	1012	87

À comparer à label.

Pour en savoir plus, consultez Apprentissage supervisé dans le cours "Introduction au Machine Learning".

croisement de caractéristiques

#fundamentals

Une caractéristique synthétique formée en "croisant" des caractéristiques catégorielles ou regroupées dans des bins.

Par exemple, prenons un modèle de "prévision de l'humeur" qui représente la température dans l'un des quatre buckets suivants :

• freezing
• chilly
• temperate
• warm

et représente la vitesse du vent dans l'un des trois buckets suivants :

• still
• light
• windy

Sans croisements de caractéristiques, le modèle linéaire s'entraîne indépendamment sur chacun des sept buckets précédents. Ainsi, le modèle s'entraîne sur freezing indépendamment de l'entraînement sur windy.

Vous pouvez également créer un croisement de caractéristiques de la température et de la vitesse du vent. Cette caractéristique synthétique aurait les 12 valeurs possibles suivantes :

• freezing-still
• freezing-light
• freezing-windy
• chilly-still
• chilly-light
• chilly-windy
• temperate-still
• temperate-light
• temperate-windy
• warm-still
• warm-light
• warm-windy

Grâce aux croisements de caractéristiques, le modèle peut apprendre les différences d'humeur entre un jour freezing-windy et un jour freezing-still.

Si vous créez une caractéristique synthétique à partir de deux caractéristiques comportant chacune de nombreux buckets différents, le croisement de caractéristiques obtenu aura un nombre énorme de combinaisons possibles. Par exemple, si une caractéristique comporte 1 000 buckets et l'autre 2 000, la caractéristique croisée résultante comporte 2 000 000 de buckets.

Formellement, un croisement est un produit cartésien.

Les croisements de caractéristiques sont principalement utilisés avec les modèles linéaires et rarement avec les réseaux de neurones.

Pour en savoir plus, consultez Données catégorielles : croisements de caractéristiques dans le Cours d'initiation au machine learning.

l'ingénierie des caractéristiques.

#fundamentals

#TensorFlow

Processus comprenant les étapes suivantes :

1. Déterminer les caractéristiques susceptibles d'être utiles pour entraîner un modèle.
2. Convertir les données brutes de l'ensemble de données en versions efficaces de ces caractéristiques.

Par exemple, vous pouvez déterminer que temperature peut être une fonctionnalité utile. Vous pouvez ensuite tester le bucketing pour optimiser ce que le modèle peut apprendre à partir de différentes plages de temperature.

L'ingénierie des caractéristiques est parfois appelée extraction de caractéristiques ou caractérisation.

Cliquez sur l'icône pour obtenir des notes supplémentaires sur TensorFlow.

Dans TensorFlow, l'ingénierie des caractéristiques implique souvent de convertir les entrées des fichiers journaux bruts en Protocol Buffers tf.Example. Voir aussi tf.Transform.

---

Pour en savoir plus, consultez Données numériques : comment un modèle ingère des données à l'aide de vecteurs de caractéristiques dans le cours intensif sur le machine learning.

ensemble de fonctionnalités

#fundamentals

Groupe des caractéristiques utilisées pour l'entraînement de votre modèle de machine learning. Par exemple, un ensemble de caractéristiques simple pour un modèle qui prédit les prix des logements peut se composer du code postal, de la taille du bien et de son état.

vecteur de caractéristiques

#fundamentals

Tableau des valeurs de caractéristiques constituant un exemple. Le vecteur de caractéristiques est saisi lors de l'entraînement et de l'inférence. Par exemple, le vecteur de caractéristiques d'un modèle comportant deux caractéristiques discrètes peut être le suivant :

[0.92, 0.56]

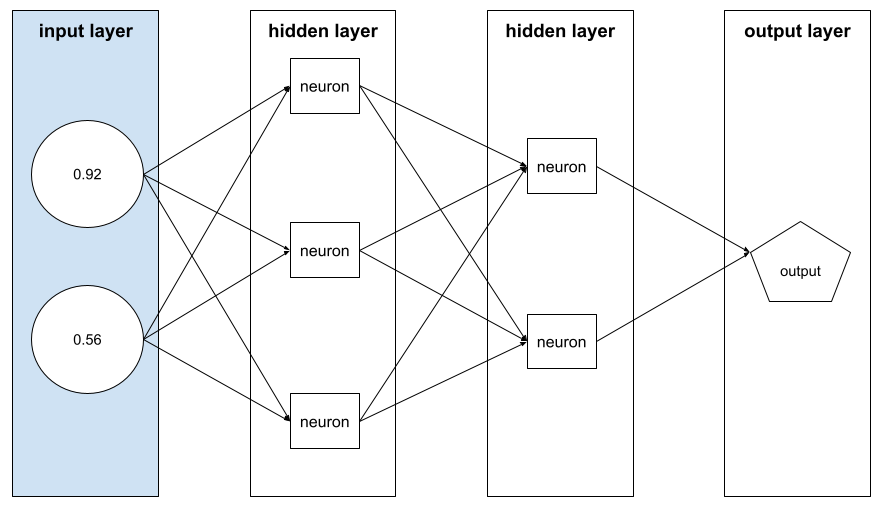
Chaque exemple fournit des valeurs différentes pour le vecteur de caractéristiques. Le vecteur de caractéristiques pour l'exemple suivant pourrait donc ressembler à ceci :

[0.73, 0.49]

L'ingénierie des caractéristiques détermine comment représenter les caractéristiques dans le vecteur de caractéristiques. Par exemple, une caractéristique catégorielle binaire avec cinq valeurs possibles peut être représentée avec un encodage one-hot. Dans ce cas, la partie du vecteur de caractéristiques pour un exemple particulier se composerait de quatre zéros et d'un seul 1.0 à la troisième position, comme suit :

[0.0, 0.0, 1.0, 0.0, 0.0]

Prenons un autre exemple. Supposons que votre modèle se compose de trois caractéristiques :

• une caractéristique catégorielle binaire avec cinq valeurs possibles représentées avec l'encodage one-hot (par exemple, [0.0, 1.0, 0.0, 0.0, 0.0]) ;
• une autre caractéristique catégorielle binaire avec trois valeurs possibles représentées avec l'encodage one-hot, par exemple : [0.0, 0.0, 1.0].
• une caractéristique à virgule flottante, par exemple : 8.3.

Dans ce cas, le vecteur de caractéristiques de chaque exemple serait représenté par neuf valeurs. Compte tenu des exemples de valeurs de la liste précédente, le vecteur de caractéristiques serait le suivant :

0.0
1.0
0.0
0.0
0.0
0.0
0.0
1.0
8.3

Pour en savoir plus, consultez Données numériques : comment un modèle ingère des données à l'aide de vecteurs de caractéristiques dans le cours intensif sur le machine learning.

boucle de rétroaction

#fundamentals

En machine learning, situation dans laquelle les prédictions d'un modèle influencent les données d'entraînement du même modèle ou d'un autre modèle. Par exemple, un modèle qui recommande des films influencera les films que les utilisateurs verront, ce qui influencera ensuite les modèles de recommandation de films ultérieurs.

Pour en savoir plus, consultez Systèmes de ML de production : questions à poser dans le cours d'initiation au machine learning.

G

généralisation

#fundamentals

Capacité d'un modèle à effectuer des prédictions correctes pour des données nouvelles, qui n'ont encore jamais été vues. Un modèle capable de généraliser est l'opposé d'un modèle en surapprentissage.

Cliquez sur l'icône pour afficher des notes supplémentaires.

Vous entraînez un modèle sur les exemples de l'ensemble d'entraînement. Par conséquent, le modèle apprend les particularités des données de l'ensemble d'entraînement. La généralisation consiste essentiellement à déterminer si votre modèle peut faire de bonnes prédictions sur des exemples qui ne figurent pas dans l'ensemble d'entraînement.

Pour encourager la généralisation, la régularisation aide un modèle à s'entraîner de manière moins précise sur les particularités des données de l'ensemble d'entraînement.

---

Pour en savoir plus, consultez Généralisation dans le cours d'initiation au machine learning.

courbe de généralisation

#fundamentals

Graphique de la perte d'entraînement et de la perte de validation en fonction du nombre d'itérations.

Une courbe de généralisation peut vous aider à détecter un éventuel surapprentissage. Par exemple, la courbe de généralisation suivante suggère un surapprentissage, car la perte de validation devient finalement beaucoup plus élevée que la perte d'entraînement.

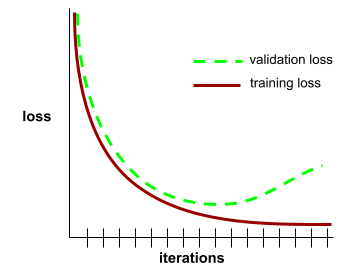
Pour en savoir plus, consultez Généralisation dans le cours d'initiation au machine learning.

descente de gradient

#fundamentals

Technique mathématique permettant de minimiser la perte. La descente de gradient ajuste de manière itérative les pondérations et les biais afin de trouver progressivement la meilleure combinaison pour minimiser la perte.

La descente de gradient est beaucoup plus ancienne que le machine learning.

Pour en savoir plus, consultez la section Régression linéaire : descente de gradient du cours d'initiation au machine learning.

vérité terrain

#fundamentals

La réalité.

Ce qui s'est réellement passé

Prenons l'exemple d'un modèle de classification binaire qui prédit si un étudiant en première année d'université obtiendra son diplôme dans les six ans. La vérité terrain pour ce modèle est de savoir si l'élève a obtenu son diplôme dans les six ans.

Cliquez sur l'icône pour afficher des notes supplémentaires.

Nous évaluons la qualité du modèle par rapport à la vérité terrain. Toutefois, la vérité terrain n'est pas toujours complètement, eh bien, vraie. Par exemple, voici quelques exemples d'imperfections potentielles dans la vérité terrain :

• Dans l'exemple de remise de diplôme, sommes-nous certains que les dossiers de remise de diplôme de chaque élève sont toujours corrects ? L'université tient-elle des registres impeccables ?
• Supposons que le libellé soit une valeur à virgule flottante mesurée par des instruments (par exemple, des baromètres). Comment pouvons-nous être sûrs que chaque instrument est calibré de manière identique ou que chaque lecture a été effectuée dans les mêmes circonstances ?
• Si le libellé est une question d'opinion humaine, comment pouvons-nous être sûrs que chaque évaluateur évalue les événements de la même manière ? Pour améliorer la cohérence, des évaluateurs humains experts interviennent parfois.

---

H

couche cachée

#fundamentals

Couche d'un réseau de neurones entre la couche d'entrée (les caractéristiques) et la couche de sortie (la prédiction). Chaque couche cachée est constituée d'un ou plusieurs neurones. Par exemple, le réseau de neurones suivant contient deux couches cachées, la première avec trois neurones et la seconde avec deux neurones :

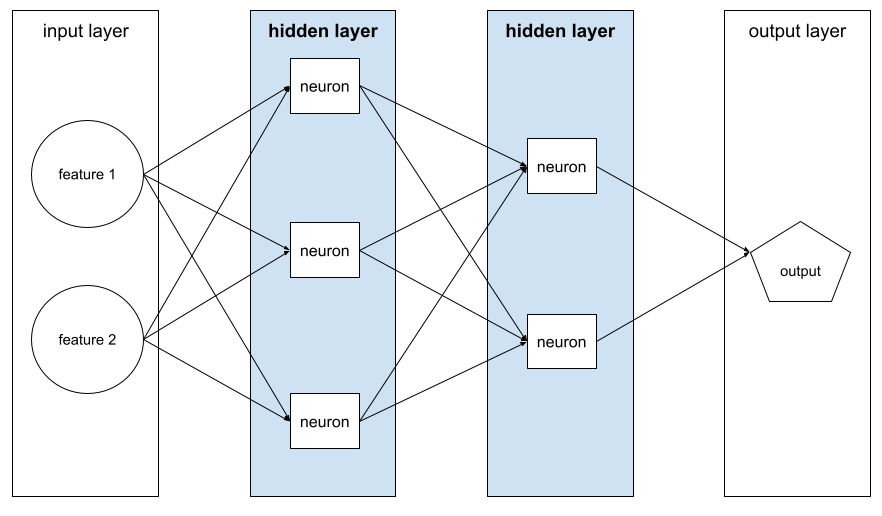
Un réseau de neurones profond contient plus d'une couche cachée. Par exemple, l'illustration précédente est un réseau de neurones profond, car le modèle contient deux couches cachées.

Pour en savoir plus, consultez Réseaux de neurones : nœuds et couches cachées dans le Cours d'initiation au Machine Learning.

hyperparamètre

#fundamentals

Variables que vous ou un service de réglage des hyperparamètres ajustez lors des exécutions successives de l'entraînement d'un modèle. Le taux d'apprentissage, par exemple, est un hyperparamètre. Vous pouvez définir le taux d'apprentissage sur 0,01 avant une session d'entraînement. Si vous déterminez que 0,01 est trop élevé, vous pouvez peut-être définir le taux d'apprentissage sur 0,003 pour la prochaine session d'entraînement.

En revanche, les paramètres sont les différents poids et biais que le modèle apprend pendant l'entraînement.

Pour en savoir plus, consultez Régression linéaire : hyperparamètres dans le Cours d'initiation au Machine Learning.

I

variables indépendantes et identiquement distribuées (i.i.d)

#fundamentals

Données issues d'une distribution qui ne change pas et où chaque valeur tirée ne dépend pas des valeurs tirées précédemment. Un i.i.d. est le gaz parfait du machine learning : c'est une construction mathématique utile qui ne se rencontre quasiment jamais à l'identique dans le monde réel. Par exemple, la distribution des visiteurs d'une page Web peut être une variable idd sur une courte période, c'est-à-dire que la distribution ne change pas pendant cette période et que la visite d'un internaute est généralement indépendante de la visite d'un autre. Toutefois, si vous élargissez cette période, des différences saisonnières peuvent apparaître dans les visiteurs de la page Web.

Voir aussi non-stationnarité.

inférence

#fundamentals

#generativeAI

Dans le machine learning traditionnel, processus consistant à effectuer des prédictions en appliquant un modèle entraîné à des exemples sans étiquette. Pour en savoir plus, consultez Apprentissage supervisé dans le cours d'introduction au ML.

Dans les grands modèles de langage, l'inférence est le processus d'utilisation d'un modèle entraîné pour générer une réponse à une requête d'entrée.

L'inférence a une signification quelque peu différente en statistiques. Pour en savoir plus, consultez l' article Wikipédia sur l'inférence statistique.

couche d'entrée

#fundamentals

La couche d'un réseau de neurones qui contient le vecteur de caractéristiques. Autrement dit, la couche d'entrée fournit des exemples pour l'entraînement ou l'inférence. Par exemple, la couche d'entrée du réseau de neurones suivant se compose de deux caractéristiques :

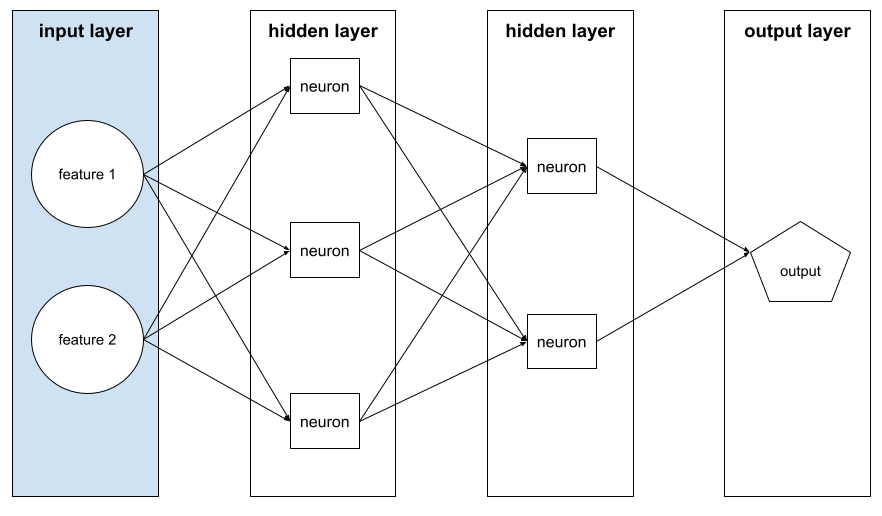
interprétabilité

#fundamentals

Capacité à expliquer ou à présenter le raisonnement d'un modèle de ML en termes compréhensibles pour un humain.

La plupart des modèles de régression linéaire, par exemple, sont très interprétables. (Il suffit d'examiner les pondérations entraînées pour chaque fonctionnalité.) Les forêts de décision sont également très interprétables. Cependant, certains modèles nécessitent des visualisations complexes pour pouvoir être interprétés.

Vous pouvez utiliser le Learning Interpretability Tool (LIT) pour interpréter les modèles de ML.

itération

#fundamentals

Mise à jour unique des paramètres d'un modèle (pondérations et biais) pendant l'entraînement. La taille du lot détermine le nombre d'exemples que le modèle traite en une seule itération. Par exemple, si la taille de lot est de 20, le modèle traite 20 exemples avant d'ajuster les paramètres.

Lors de l'entraînement d'un réseau de neurones, une seule itération implique les deux passes suivantes :

1. Transmission directe pour évaluer la perte sur un seul lot.
2. Un passage à rebours (rétropropagation) pour ajuster les paramètres du modèle en fonction de la perte et du taux d'apprentissage.

Pour en savoir plus, consultez la section Descente de gradient du cours d'initiation au machine learning.

L

Régularisation L₀

#fundamentals

Type de régularisation qui pénalise le nombre total de pondérations non nulles dans un modèle. Par exemple, un modèle comportant 11 pondérations non nulles sera plus pénalisé qu'un modèle similaire comportant 10 pondérations non nulles.

La régularisation L₀ est parfois appelée régularisation de la norme L0.

Cliquez sur l'icône pour afficher des notes supplémentaires.

_{La régularisation L0 est généralement peu pratique dans les grands modèles, car elle transforme l'entraînement en un problème d'optimisation convexe.}

---

Perte L₁

#fundamentals

#Metric

Fonction de perte qui calcule la valeur absolue de la différence entre les valeurs d'étiquette réelles et les valeurs prédites par un modèle. Par exemple, voici le calcul de la perte L₁ pour un batch de cinq exemples :

Valeur réelle de l'exemple	Valeur prédite du modèle	Valeur absolue du delta
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = perte L1

La perte L₁ est moins sensible aux valeurs aberrantes que la perte L₂.

L'erreur absolue moyenne correspond à la perte L₁ moyenne par exemple.

Cliquez sur l'icône pour afficher la formule mathématique.

$$ L_1 loss = \sum_{i=0}^n | y_i - \hat{y}_i |$$

où :

• $n$ correspond au nombre d'exemples.
• $y$ est la valeur réelle du libellé.
• $\hat{y}$ est la valeur que le modèle prédit pour $y$.

---

Pour en savoir plus, consultez Régression linéaire : perte dans le cours d'initiation au machine learning.

Régularisation L₁

#fundamentals

Type de régularisation qui pénalise les pondérations proportionnellement à la somme de leurs valeurs absolues. La régularisation L₁ aide à mettre à zéro les pondérations des caractéristiques peu ou pas pertinentes. Une caractéristique avec un poids de 0 est effectivement supprimée du modèle.

À comparer à la régularisation _L2.

Perte L₂

#fundamentals

#Metric

Une fonction de perte qui calcule le carré de la différence entre les valeurs d'étiquette réelles et les valeurs prédites par un modèle. Par exemple, voici le calcul de la perte L₂ pour un batch de cinq exemples :

Valeur réelle de l'exemple	Valeur prédite du modèle	Carré du delta
7	6	1
5	4	1
8	11	9
4	6	4
9	8	1
		16 = perte L2

En raison de la mise au carré, la perte L₂ amplifie l'influence des valeurs aberrantes. En d'autres termes, la perte L₂ réagit plus fortement aux mauvaises prédictions que la perte L₁. Par exemple, la perte L₁ pour le lot précédent serait de 8 au lieu de 16. Notez qu'une seule valeur aberrante représente 9 des 16 valeurs.

Les modèles de régression utilisent généralement la perte L₂ comme fonction de perte.

L'erreur quadratique moyenne correspond à la perte L₂ moyenne par exemple. La perte quadratique est un autre nom pour la perte L₂.

Cliquez sur l'icône pour afficher la formule mathématique.

$$ L_2 loss = \sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$

où :

• $n$ correspond au nombre d'exemples.
• $y$ est la valeur réelle du libellé.
• $\hat{y}$ est la valeur que le modèle prédit pour $y$.

---

Pour en savoir plus, consultez Régression logistique : perte et régularisation dans le Cours d'initiation au machine learning.

Régularisation L₂

#fundamentals

Type de régularisation qui pénalise les pondérations proportionnellement à la somme des carrés des pondérations. La régularisation L₂ aide à rapprocher de zéro la pondération des valeurs aberrantes (celles dont la valeur est très positive ou très négative), sans pour autant atteindre zéro. Les caractéristiques dont les valeurs sont très proches de 0 restent dans le modèle, mais n'ont pas beaucoup d'influence sur la prédiction du modèle.

La régularisation L₂ améliore toujours la généralisation dans les modèles linéaires.

À comparer à la régularisation _L1.

Pour en savoir plus, consultez Surapprentissage : régularisation L2 dans le cours d'initiation au machine learning.

étiquette

#fundamentals

Dans l'apprentissage supervisé, "réponse" ou "résultat" d'un exemple.

Chaque exemple étiqueté se compose d'une ou plusieurs caractéristiques et d'une étiquette. Par exemple, dans un ensemble de données de détection de spam, l'étiquette serait probablement "spam" ou "non spam". Dans un ensemble de données sur les précipitations, le libellé peut correspondre à la quantité de pluie tombée au cours d'une période donnée.

Pour en savoir plus, consultez Apprentissage supervisé dans "Introduction au machine learning".

exemple étiqueté

#fundamentals

Exemple contenant une ou plusieurs caractéristiques et un libellé. Par exemple, le tableau suivant présente trois exemples étiquetés d'un modèle d'évaluation de maisons, chacun avec trois caractéristiques et une étiquette :

Nombre de chambres	Nombre de salles de bain	Âge de la maison	Prix de la maison (libellé)
3	2	15	$345,000
2	1	72	179 000 $
4	2	34	392 000 $

Dans le machine learning supervisé, les modèles sont entraînés sur des exemples étiquetés et effectuent des prédictions sur des exemples sans étiquette.

Comparer un exemple étiqueté avec des exemples non étiquetés.

Pour en savoir plus, consultez Apprentissage supervisé dans "Introduction au machine learning".

lambda

#fundamentals

Synonyme de taux de régularisation.

Lambda est un terme surchargé. Ici, nous nous référons à sa définition dans le cadre de la régularisation.

cachée)

#fundamentals

Ensemble de neurones dans un réseau de neurones. Voici trois types de calques courants :

• La couche d'entrée, qui fournit des valeurs pour toutes les caractéristiques.
• Une ou plusieurs couches cachées, qui trouvent des relations non linéaires entre les caractéristiques et l'étiquette.
• La couche de sortie, qui fournit la prédiction.

Par exemple, l'illustration suivante montre un réseau de neurones avec une couche d'entrée, deux couches cachées et une couche de sortie :

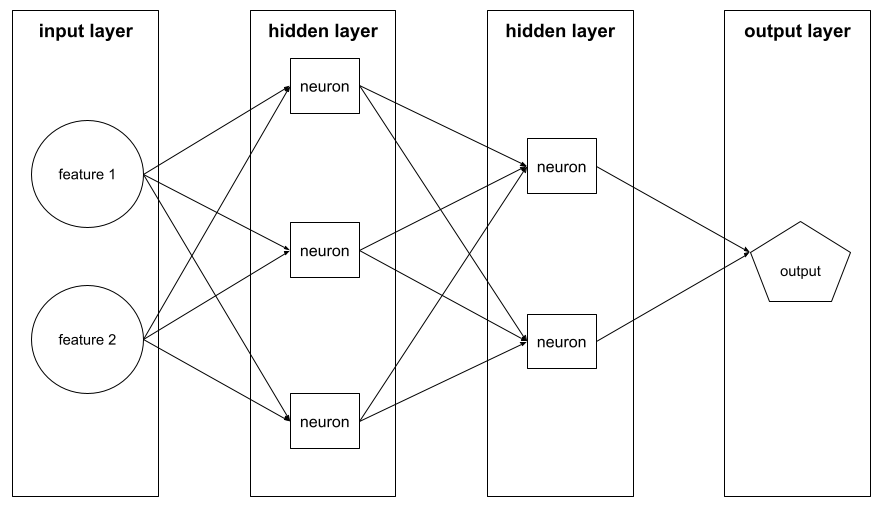
Dans TensorFlow, les couches sont également des fonctions Python qui prennent des Tensors et des options de configuration en entrée pour générer d'autres Tensors en sortie.

taux d'apprentissage

#fundamentals

Nombre à virgule flottante qui indique à l'algorithme de descente de gradient l'ampleur de l'ajustement des pondérations et des biais à chaque itération. Par exemple, un taux d'apprentissage de 0,3 ajusterait les pondérations et les biais trois fois plus fortement qu'un taux d'apprentissage de 0,1.

Le taux d'apprentissage est un hyperparamètre clé. Si vous définissez un taux d'apprentissage trop faible, l'entraînement prendra trop de temps. Si vous définissez un taux d'apprentissage trop élevé, la descente de gradient a souvent du mal à atteindre la convergence.

Cliquez sur l'icône pour obtenir une explication plus mathématique.

À chaque itération, l'algorithme de descente de gradient multiplie le taux d'apprentissage par le gradient. Le produit obtenu est appelé étape de gradient.

---

Pour en savoir plus, consultez Régression linéaire : hyperparamètres dans le Cours d'initiation au Machine Learning.

linear

#fundamentals

Relation entre deux variables ou plus qui peut être représentée uniquement par l'addition et la multiplication.

Le graphique d'une relation linéaire est une ligne.

À comparer à non linéaire.

modèle linéaire

#fundamentals

Un modèle qui attribue une pondération par caractéristique pour effectuer des prédictions. (Les modèles linéaires intègrent également un biais.) En revanche, la relation entre les caractéristiques et les prédictions dans les modèles profonds est généralement non linéaire.

Les modèles linéaires sont généralement plus faciles à entraîner et plus interprétables que les modèles profonds. Toutefois, les modèles profonds peuvent apprendre des relations complexes entre les caractéristiques.

La régression linéaire et la régression logistique sont deux types de modèles linéaires.

Cliquez sur l'icône pour afficher le calcul.

Un modèle linéaire suit la formule suivante :

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

où :

• y' est la prédiction brute. (Dans certains types de modèles linéaires, cette prédiction brute sera modifiée. Par exemple, consultez Régression logistique.
• b correspond au biais.
• w est une pondération. w₁ est donc la pondération de la première caractéristique, w₂ est la pondération de la deuxième caractéristique, et ainsi de suite.
• x est une caractéristique. Par conséquent, x₁ est la valeur de la première caractéristique, x₂ est la valeur de la deuxième caractéristique, et ainsi de suite.

Par exemple, supposons qu'un modèle linéaire pour trois caractéristiques apprenne les biais et pondérations suivants :

• b = 7
• w₁ = -2,5
• w₂ = -1,2
• w₃ = 1,4

Par conséquent, étant donné trois caractéristiques (x₁, x₂ et x₃), le modèle linéaire utilise l'équation suivante pour générer chaque prédiction :

y' = 7 + (-2.5)(x1) + (-1.2)(x2) + (1.4)(x3)

Supposons qu'un exemple particulier contienne les valeurs suivantes :

• x₁ = 4
• x₂ = -10
• x₃ = 5

En insérant ces valeurs dans la formule, on obtient une prédiction pour cet exemple :

y' = 7 + (-2.5)(4) + (-1.2)(-10) + (1.4)(5)
y' = 16

Les modèles linéaires incluent non seulement les modèles qui utilisent uniquement une équation linéaire pour effectuer des prédictions, mais aussi un ensemble plus large de modèles qui utilisent une équation linéaire comme l'un des composants de la formule qui effectue des prédictions. Par exemple, la régression logistique post-traite la prédiction brute (y') pour produire une valeur de prédiction finale comprise entre 0 et 1, exclusive.

---

régression linéaire

#fundamentals

Type de modèle de machine learning dans lequel les deux conditions suivantes sont remplies :

• Le modèle est un modèle linéaire.
• La prédiction est une valeur à virgule flottante. (Il s'agit de la partie régression de la régression linéaire.)

Comparez la régression linéaire à la régression logistique. Comparez également la régression à la classification.

Pour en savoir plus, consultez Régression linéaire dans le Cours d'initiation au Machine Learning.

régression logistique

#fundamentals

Type de modèle de régression qui prédit une probabilité. Les modèles de régression logistique présentent les caractéristiques suivantes :

• Le libellé est catégoriel. Le terme "régression logistique" fait généralement référence à la régression logistique binaire, c'est-à-dire à un modèle qui calcule les probabilités pour les libellés avec deux valeurs possibles. La régression logistique multinomiale, une variante moins courante, calcule les probabilités pour les libellés comportant plus de deux valeurs possibles.
• La fonction de perte pendant l'entraînement est la perte logistique. (Plusieurs unités de perte logistique multiple peuvent être placées en parallèle pour les libellés comportant plus de deux valeurs possibles.)
• Le modèle possède une architecture linéaire, et non un réseau de neurones profond. Toutefois, le reste de cette définition s'applique également aux modèles profonds qui prédisent les probabilités pour les libellés de catégories.

Prenons l'exemple d'un modèle de régression logistique qui calcule la probabilité qu'un e-mail entrant soit du spam ou non. Pendant l'inférence, supposons que le modèle prédise 0,72. Le modèle estime donc :

• L'e-mail a 72 % de chances d'être un spam.
• Il y a 28 % de chances que l'e-mail ne soit pas du spam.

Un modèle de régression logistique utilise l'architecture en deux étapes suivante :

1. Le modèle génère une prédiction brute (y') en appliquant une fonction linéaire des caractéristiques d'entrée.
2. Le modèle utilise cette prédiction brute comme entrée pour une fonction sigmoïde, qui convertit la prédiction brute en une valeur comprise entre 0 et 1 (exclusivement).

Comme tout modèle de régression, un modèle de régression logistique prédit un nombre. Toutefois, ce nombre fait généralement partie d'un modèle de classification binaire comme suit :

• Si le nombre prédit est supérieur au seuil de classification, le modèle de classification binaire prédit la classe positive.
• Si le nombre prédit est inférieur au seuil de classification, le modèle de classification binaire prédit la classe négative.

Pour en savoir plus, consultez Régression logistique dans le Cours d'initiation au machine learning.

Perte logistique

#fundamentals

La fonction de perte utilisée dans la régression logistique binaire.

Cliquez sur l'icône pour afficher le calcul.

La formule suivante permet de calculer la perte logistique :

$$\text{Log Loss} = \sum_{(x,y)\in D} -y\log(y') - (1 - y)\log(1 - y')$$

où :

• \((x,y)\in D\) est l'ensemble de données contenant de nombreux exemples étiquetés, qui sont des paires \((x,y)\) .
• \(y\) est l'étiquette dans un exemple étiqueté. Puisqu'il s'agit de régression logistique, chaque valeur de \(y\) doit être 0 ou 1.
• \(y'\) est la valeur prédite (comprise entre 0 et 1, exclus), étant donné l'ensemble des caractéristiques dans \(x\).

---

Pour en savoir plus, consultez Régression logistique : perte et régularisation dans le Cours d'initiation au Machine Learning.

logarithme de cote

#fundamentals

Logarithme des chances d'un événement.

Cliquez sur l'icône pour afficher le calcul.

Si l'événement est une probabilité binaire, odds fait référence au rapport entre la probabilité de succès (p) et la probabilité d'échec (1-p). Par exemple, supposons qu'un événement donné ait 90 % de chances de succès et 10 % de chances d'échec. Dans ce cas, les cotes sont calculées de la manière suivante :

$$ {\text{odds}} = \frac{\text{p}} {\text{(1-p)}} = \frac{.9} {.1} = {\text{9}} $$

Le logarithme des cotes est simplement le logarithme des cotes. Par convention, le terme "logarithme" fait référence au logarithme naturel, mais le logarithme peut en fait être n'importe quelle base supérieure à 1. Si l'on s'en tient à la convention, le logarithme des cotes de notre exemple est donc :

$$ {\text{log-odds}} = ln(9) ~= 2.2 $$

La fonction logit est l'inverse de la fonction sigmoïde.

---

perte

#fundamentals

#Metric

Pendant l'entraînement d'un modèle supervisé, une mesure de l'écart entre la prédiction d'un modèle et son libellé.

Une fonction de perte calcule la perte.

Pour en savoir plus, consultez Régression linéaire : perte dans le cours d'initiation au machine learning.

courbe de perte

#fundamentals

Graphique de la perte en fonction du nombre d'itérations d'entraînement. Le graphique suivant montre une courbe de perte typique :

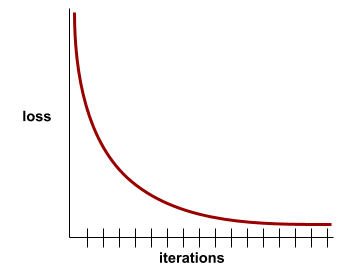
Les courbes de perte peuvent vous aider à déterminer quand votre modèle converge ou surapprend.

Les courbes de perte peuvent représenter tous les types de perte suivants :

• Perte d'entraînement
• Perte de validation
• test loss

Voir aussi courbe de généralisation.

Pour en savoir plus, consultez Surapprentissage : interpréter les courbes de perte dans le Cours d'initiation au machine learning.

fonction de perte

#fundamentals

#Metric

Pendant l'entraînement ou le test, une fonction mathématique qui calcule la perte sur un batch d'exemples. Une fonction de perte renvoie une perte plus faible pour les modèles qui font de bonnes prédictions que pour ceux qui font de mauvaises prédictions.

L'objectif de l'entraînement est généralement de minimiser la perte renvoyée par une fonction de perte.

Il existe de nombreux types de fonctions de perte. Choisissez la fonction de perte appropriée pour le type de modèle que vous créez. Exemple :

• La perte L₂ (ou erreur quadratique moyenne) est la fonction de perte pour la régression linéaire.
• La perte logistique est la fonction de perte pour la régression logistique.

M

machine learning

#fundamentals

Programme ou système qui entraîne un modèle à partir de données d'entrée. Le modèle entraîné peut faire des prédictions utiles à partir de données inédites issues de la même distribution que celle utilisée pour entraîner le modèle.

Le machine learning (ou apprentissage automatique) désigne également la discipline qui traite de ces programmes ou systèmes.

Pour en savoir plus, consultez le cours Introduction au machine learning.

classe majoritaire

#fundamentals

Étiquette la plus commune dans un ensemble de données avec déséquilibre des classes. Par exemple, pour un ensemble de données contenant 99 % d'étiquettes négatives et 1 % d'étiquettes positives, les étiquettes négatives constituent la classe majoritaire.

À comparer à la classe minoritaire.

Pour en savoir plus, consultez Ensembles de données : ensembles de données déséquilibrés dans le Cours d'initiation au Machine Learning.

mini-lot

#fundamentals

Petit sous-ensemble, sélectionné aléatoirement, d'un lot traité en une seule itération. La taille de lot d'un mini-lot est généralement comprise entre 10 et 1 000 exemples.

Par exemple, supposons que l'ensemble d'entraînement complet (le lot complet) se compose de 1 000 exemples. Supposons également que vous définissez la taille de lot de chaque mini-lot sur 20. Par conséquent, chaque itération détermine la perte sur 20 exemples aléatoires sur les 1 000,puis ajuste les poids et les biais en conséquence.

Il est bien plus efficace de calculer la perte pour un mini-lot que pour l'ensemble des exemples du lot complet.

Pour en savoir plus, consultez Régression linéaire : hyperparamètres dans le Cours d'initiation au Machine Learning.

classe minoritaire

#fundamentals

Étiquette la moins commune dans un ensemble de données avec déséquilibre des classes. Par exemple, pour un ensemble de données contenant 99 % d'étiquettes négatives et 1 % d'étiquettes positives, les étiquettes positives constituent la classe minoritaire.

À comparer à la classe majoritaire.

Cliquez sur l'icône pour afficher des notes supplémentaires.

Un ensemble d'entraînement avec un million d'exemples semble impressionnant. Toutefois, si la classe minoritaire est mal représentée, même un ensemble d'entraînement très volumineux peut s'avérer insuffisant. Concentrez-vous moins sur le nombre total d'exemples dans l'ensemble de données et davantage sur le nombre d'exemples dans la classe minoritaire.

Si votre ensemble de données ne contient pas suffisamment d'exemples de la classe minoritaire, envisagez d'utiliser le sous-échantillonnage (définition dans le deuxième point) pour compléter la classe minoritaire.

---

Pour en savoir plus, consultez Ensembles de données : ensembles de données déséquilibrés dans le Cours d'initiation au Machine Learning.

modèle

#fundamentals

En général, toute construction mathématique qui traite des données d'entrée et renvoie des données de sortie. En d'autres termes, un modèle est l'ensemble des paramètres et de la structure nécessaires à un système pour effectuer des prédictions. Dans le machine learning supervisé, un modèle prend un exemple comme entrée et infère une prédiction comme sortie. Dans l'apprentissage automatique supervisé, les modèles diffèrent quelque peu. Exemple :

• Un modèle de régression linéaire se compose d'un ensemble de pondérations et d'un biais.
• Un modèle de réseau de neurones se compose des éléments suivants :
  • Un ensemble de couches cachées, chacune contenant un ou plusieurs neurones.
  • Les pondérations et le biais associés à chaque neurone.
• Un modèle en arbre de décision se compose des éléments suivants :
  • Forme de l'arbre, c'est-à-dire le schéma selon lequel les conditions et les feuilles sont connectées.
  • Conditions et feuilles

Vous pouvez enregistrer, restaurer ou copier un modèle.

Le machine learning non supervisé génère également des modèles, généralement une fonction qui peut mapper un exemple d'entrée au cluster le plus approprié.

Cliquez sur l'icône pour comparer les fonctions algébriques et de programmation aux modèles de ML.

Une fonction algébrique telle que la suivante est un modèle :

  f(x, y) = 3x -5xy + y2 + 17

La fonction précédente mappe les valeurs d'entrée (x et y) à la sortie.

De même, une fonction de programmation comme celle-ci est également un modèle :

def half_of_greater(x, y):
  if (x > y):
    return(x / 2)
  else
    return(y / 2)

Un appelant transmet des arguments à la fonction Python précédente, et la fonction Python génère une sortie (via l'instruction return).

Bien qu'un réseau de neurones profond ait une structure mathématique très différente de celle d'une fonction algébrique ou de programmation, il prend toujours une entrée (un exemple) et renvoie une sortie (une prédiction).

Un programmeur humain code manuellement une fonction de programmation. En revanche, un modèle de machine learning apprend progressivement les paramètres optimaux lors de l'entraînement automatisé.

---

classification à classes multiples

#fundamentals

Dans l'apprentissage supervisé, un problème de classification dans lequel l'ensemble de données contient plus de deux classes d'étiquettes. Par exemple, les libellés de l'ensemble de données Iris doivent appartenir à l'une des trois classes suivantes :

• Iris setosa
• Iris virginica
• Iris versicolor

Un modèle entraîné sur l'ensemble de données Iris qui prédit le type d'iris sur de nouveaux exemples effectue une classification à classes multiples.

En revanche, les problèmes de classification qui font la distinction entre exactement deux classes sont des modèles de classification binaire. Par exemple, un modèle d'e-mails qui prédit si un e-mail est du spam ou non-spam est un modèle de classification binaire.

Dans les problèmes de clustering, la classification multiclasse fait référence à plus de deux clusters.

Pour en savoir plus, consultez Réseaux de neurones : classification multiclasse dans le cours d'initiation au machine learning.

N

classe négative

#fundamentals

#Metric

Dans la classification binaire, une classe est dite positive et l'autre négative. La classe positive est l'élément ou l'événement que le modèle teste, et la classe négative est l'autre possibilité. Exemple :

• La classe négative d'un test médical pourrait être "pas une tumeur".
• La classe négative d'un modèle de classification d'e-mails peut être "non-spam".

À comparer à la classe positive.

neurones feedforward

#fundamentals

Un modèle contenant au moins une couche cachée. Un réseau de neurones profond est un type de réseau de neurones contenant plus d'une couche cachée. Par exemple, le diagramme suivant montre un réseau de neurones profonds contenant deux couches cachées.

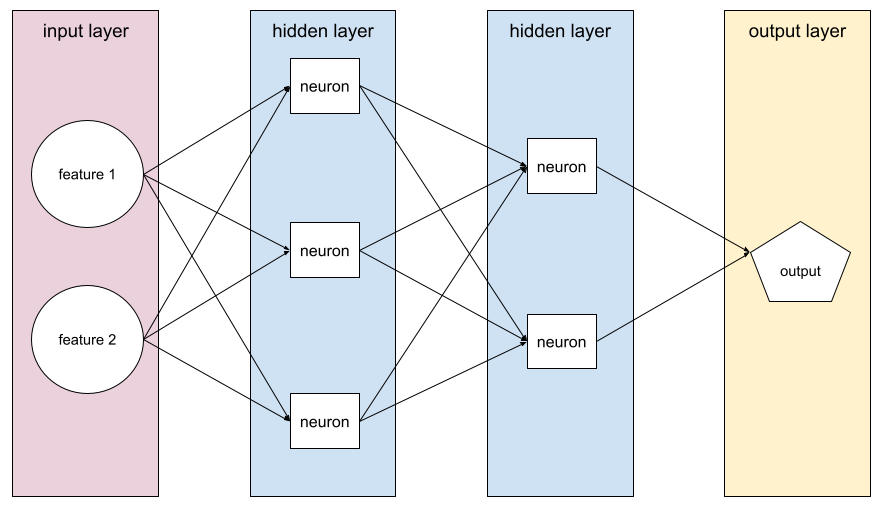
Chaque neurone d'un réseau de neurones se connecte à tous les nœuds de la couche suivante. Par exemple, dans le diagramme précédent, notez que chacun des trois neurones de la première couche cachée se connecte séparément aux deux neurones de la deuxième couche cachée.

Les réseaux de neurones implémentés sur des ordinateurs sont parfois appelés réseaux de neurones artificiels pour les différencier des réseaux de neurones présents dans le cerveau et d'autres systèmes nerveux.

Certains réseaux de neurones peuvent imiter des relations non linéaires extrêmement complexes entre différentes caractéristiques et le libellé.

Consultez également Réseau de neurones convolutif et Réseau de neurones récurrent.

Pour en savoir plus, consultez la section Réseaux de neurones du cours d'initiation au machine learning.

neurone

#fundamentals

En machine learning, une unité distincte au sein d'une couche cachée d'un réseau de neurones. Chaque neurone effectue les deux actions suivantes :

1. Calcule la somme pondérée des valeurs d'entrée multipliées par leurs pondérations correspondantes.
2. Transmet la somme pondérée en tant qu'entrée à une fonction d'activation.

Un neurone de la première couche cachée accepte les entrées des valeurs de caractéristiques dans la couche d'entrée. Un neurone de n'importe quelle couche cachée au-delà de la première accepte les entrées des neurones de la couche cachée précédente. Par exemple, un neurone de la deuxième couche cachée accepte les entrées des neurones de la première couche cachée.

L'illustration suivante met en évidence deux neurones et leurs entrées.

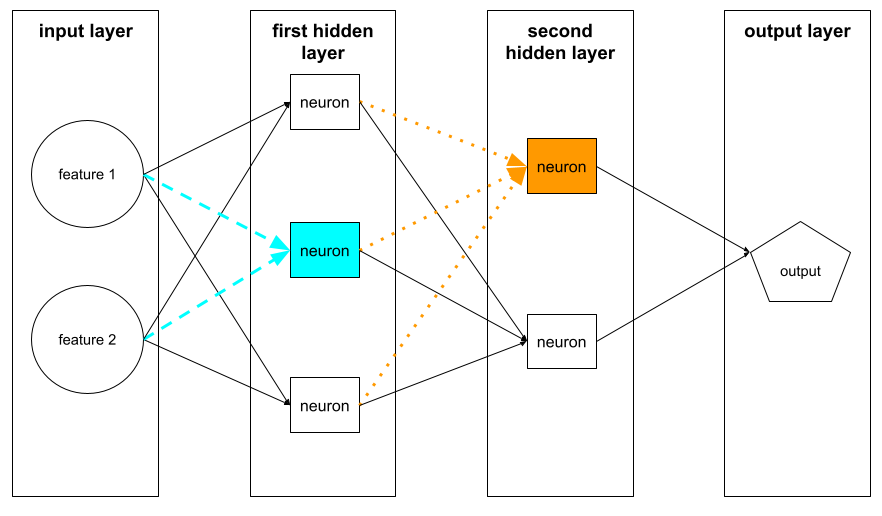
Un neurone dans un réseau de neurones imite le comportement des neurones dans le cerveau et d'autres parties du système nerveux.

nœud (réseau de neurones)

#fundamentals

Un neurone dans une couche cachée.

Pour en savoir plus, consultez Réseaux de neurones dans le Cours d'initiation au Machine Learning.

non linéaire

#fundamentals

Relation entre deux variables ou plus qui ne peut pas être représentée uniquement par l'addition et la multiplication. Une relation linéaire peut être représentée sous la forme d'une ligne, contrairement à une relation non linéaire. Prenons l'exemple de deux modèles qui associent chacun une seule caractéristique à un seul libellé. Le modèle de gauche est linéaire et celui de droite est non linéaire :

Consultez Réseaux de neurones : nœuds et couches cachées dans le cours d'initiation au machine learning pour tester différents types de fonctions non linéaires.

non-stationnarité

#fundamentals

Caractéristique dont les valeurs changent selon une ou plusieurs dimensions, généralement le temps. Par exemple, voici quelques exemples de non-stationnarité :

• Le nombre de maillots de bain vendus dans un magasin donné varie selon la saison.
• La quantité d'un fruit particulier récolté dans une région donnée est nulle pendant la majeure partie de l'année, mais importante pendant une brève période.
• En raison du changement climatique, les températures moyennes annuelles évoluent.

À comparer à la stationnarité.

normalisation

#fundamentals

De manière générale, le processus de conversion de la plage de valeurs réelle d'une variable en une plage de valeurs standard, par exemple :

• -1 à +1
• Entre 0 et 1
• Scores Z (environ de -3 à +3)

Par exemple, supposons que la plage de valeurs réelle d'une caractéristique donnée soit comprise entre 800 et 2 400. Dans le cadre de l'ingénierie des caractéristiques, vous pouvez normaliser les valeurs réelles dans une plage standard, par exemple de -1 à +1.

La normalisation est une tâche courante dans l'ingénierie des caractéristiques. Les modèles s'entraînent généralement plus rapidement (et produisent de meilleures prédictions) lorsque chaque caractéristique numérique du vecteur de caractéristiques a à peu près la même plage.

Voir aussi Normalisation du score Z.

Pour en savoir plus, consultez Données numériques : normalisation dans le Cours d'initiation au machine learning.

données numériques

#fundamentals

Caractéristiques représentées par des nombres entiers ou réels. Par exemple, un modèle d'évaluation de maison représenterait probablement la taille d'une maison (en pieds carrés ou en mètres carrés) sous forme de données numériques. Représenter une caractéristique sous forme de données numériques indique que les valeurs de la caractéristique ont une relation mathématique avec le libellé. Autrement dit, le nombre de mètres carrés d'une maison est probablement lié mathématiquement à sa valeur.

Toutes les données entières ne doivent pas être représentées sous forme de données numériques. Par exemple, les codes postaux de certaines régions du monde sont des nombres entiers. Toutefois, les codes postaux entiers ne doivent pas être représentés comme des données numériques dans les modèles. En effet, un code postal 20000 n'est pas deux fois (ou moitié) plus puissant qu'un code postal 10000. De plus, bien que différents codes postaux correspondent à différentes valeurs immobilières, nous ne pouvons pas supposer que les valeurs immobilières du code postal 20000 sont deux fois plus élevées que celles du code postal 10000. Les codes postaux doivent être représentés par des données catégorielles.

Les caractéristiques numériques sont parfois appelées caractéristiques continues.

Pour en savoir plus, consultez Utiliser des données numériques dans le Cours d'initiation au Machine Learning.

O

Hors connexion

#fundamentals

Synonyme de statique.

inférence hors connexion

#fundamentals

Processus par lequel un modèle génère un lot de prédictions, puis met ces prédictions en cache (les enregistre). Les applications peuvent ensuite accéder à la prédiction inférée à partir du cache au lieu de réexécuter le modèle.

Prenons l'exemple d'un modèle qui génère des prévisions météo locales (prédictions) toutes les quatre heures. Après chaque exécution du modèle, le système met en cache toutes les prévisions météo locales. Les applications météo récupèrent les prévisions à partir du cache.

L'inférence hors connexion est également appelée inférence statique.

À comparer à l'inférence en ligne. Pour en savoir plus, consultez Systèmes de ML de production : inférence statique ou dynamique dans le Cours d'initiation au machine learning.

Encodage one-hot

#fundamentals

Représentation des données catégorielles sous forme de vecteur dans lequel :

• Un élément est défini sur 1.
• Tous les autres éléments sont définis sur 0.

L'encodage one-hot est couramment utilisé pour représenter des chaînes ou des identifiants qui ont un ensemble fini de valeurs possibles. Par exemple, supposons qu'une certaine caractéristique catégorielle nommée Scandinavia comporte cinq valeurs possibles :

• "Danemark"
• "Suède"
• "Norvège"
• "Finlande"
• "Islande"

L'encodage one-hot pourrait représenter chacune des cinq valeurs comme suit :

Pays	Vecteur
"Danemark"	1	0	0	0	0
"Suède"	0	1	0	0	0
"Norvège"	0	0	1	0	0
"Finlande"	0	0	0	1	0
"Islande"	0	0	0	0	1

Grâce à l'encodage one-hot, un modèle peut apprendre différentes connexions en fonction de chacun des cinq pays.

Représenter une caractéristique sous forme de données numériques est une alternative à l'encodage one-hot. Malheureusement, représenter les pays scandinaves numériquement n'est pas un bon choix. Par exemple, prenons la représentation numérique suivante :

• "Denmark" (Danemark) est défini sur 0.
• "Sweden" est 1
• "Norvège" est 2
• "Finlande" est 3
• "Islande" est 4

Avec l'encodage numérique, un modèle interpréterait les nombres bruts de manière mathématique et tenterait de s'entraîner sur ces nombres. Cependant, l'Islande n'est pas deux fois plus (ou deux fois moins) que la Norvège. Le modèle tirerait donc des conclusions étranges.

Pour en savoir plus, consultez Données catégorielles : vocabulaire et encodage one-hot dans le Cours d'initiation au Machine Learning.

un contre tous

#fundamentals

Face à un problème de classification avec N classes, une solution consiste en N modèles de classification binaire distincts : un modèle de classification binaire pour chaque résultat possible. Soit, par exemple, un modèle qui classe les exemples en animal, végétal ou minéral. Une solution un contre tous fournirait les trois modèles de classification binaire distincts suivants :

• animal ou non
• légume ou non
• minéral ou non minéral

online

#fundamentals

Synonyme de dynamique.

inférence en ligne

#fundamentals

Génération de prédictions à la demande. Par exemple, supposons qu'une application transmette une entrée à un modèle et émette une demande de prédiction. Un système utilisant l'inférence en ligne répond à la requête en exécutant le modèle (et en renvoyant la prédiction à l'application).

À comparer à l'inférence hors connexion.

Pour en savoir plus, consultez Systèmes de ML de production : inférence statique ou dynamique dans le Cours d'initiation au machine learning.

couche de sortie

#fundamentals

Couche "finale" d'un réseau de neurones. La couche de sortie contient la prédiction.

L'illustration suivante montre un petit réseau de neurones profond avec une couche d'entrée, deux couches cachées et une couche de sortie :

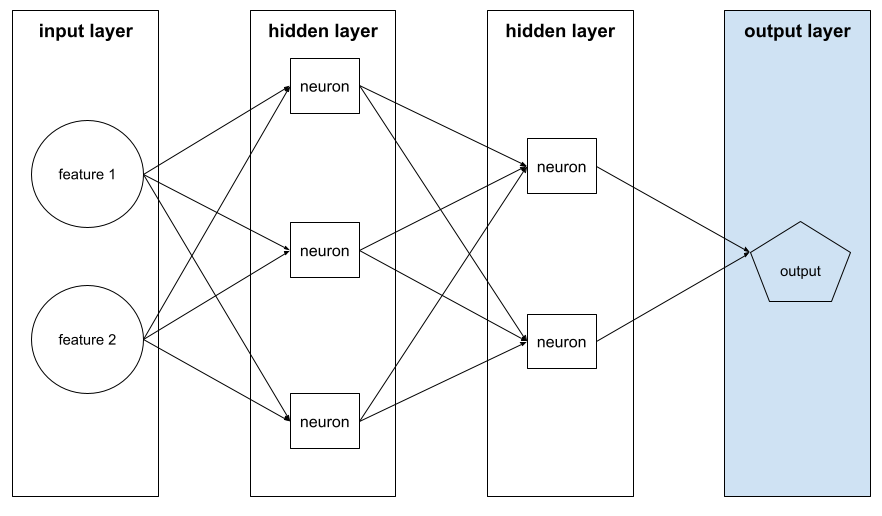
surapprentissage

#fundamentals

Création d'un modèle correspondant si étroitement aux données d'entraînement qu'il ne parvient pas à effectuer des prédictions correctes avec de nouvelles données.

La régularisation peut réduire le surapprentissage. L'entraînement sur un ensemble d'entraînement vaste et diversifié peut également réduire le surapprentissage.

Cliquez sur l'icône pour afficher des notes supplémentaires.

Le surapprentissage, c'est comme suivre strictement les conseils de votre professeur préféré. Vous réussirez probablement dans le cours de cet enseignant, mais vous risquez de vous "suradapter" à ses idées et d'échouer dans d'autres cours. En suivant les conseils de plusieurs enseignants, vous pourrez mieux vous adapter aux nouvelles situations.

---

Pour en savoir plus, consultez Surapprentissage dans le Cours d'initiation au Machine Learning.

P

pandas

#fundamentals

API d'analyse de données orientée colonnes, basée sur numpy. De nombreux frameworks de machine learning, y compris TensorFlow, acceptent les structures de données pandas comme entrées. Pour en savoir plus, consultez la documentation de pandas.

paramètre

#fundamentals

Les pondérations et les biais qu'un modèle apprend lors de l'entraînement. Par exemple, dans un modèle de régression linéaire, les paramètres se composent du biais (b) et de toutes les pondérations (w₁, w₂, etc.) dans la formule suivante :

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

En revanche, les hyperparamètres sont les valeurs que vous (ou un service de réglage d'hyperparamètres) fournissez au modèle. Le taux d'apprentissage, par exemple, est un hyperparamètre.

classe positive

#fundamentals

#Metric

Classe pour laquelle vous effectuez le test.

Par exemple, la classe positive d'un modèle de détection du cancer pourrait être "tumeur". La classe positive d'un modèle de classification d'e-mails peut être "spam".

À comparer à la classe négative.

Cliquez sur l'icône pour afficher des notes supplémentaires.

Le terme classe positive peut être déroutant, car le résultat "positif" de nombreux tests est souvent indésirable. Par exemple, la classe positive de nombreux tests médicaux correspond aux tumeurs ou aux maladies. En général, vous souhaitez qu'un médecin vous dise : "Félicitations ! Les résultats de votre test sont négatifs." Dans tous les cas, la classe positive correspond à l'événement que le test cherche à identifier.

Certes, vous testez simultanément les classes positives et négatives.

---

post-traitement

#responsible

#fundamentals

Ajuster la sortie d'un modèle après son exécution. Le post-traitement peut être utilisé pour appliquer des contraintes d'équité sans modifier les modèles eux-mêmes.

Par exemple, il est possible d'appliquer un post-traitement à un modèle de classification binaire en définissant un seuil de classification de sorte que l'égalité des chances soit maintenue pour un attribut donné en vérifiant que le taux de vrais positifs est le même pour toutes les valeurs de cet attribut.

precision

#fundamentals

#Metric

Statistique des modèles de classification qui répond à la question suivante :

Lorsque le modèle a prédit la classe positive, quel pourcentage de prédictions étaient correctes ?

Voici la formule :

$$\text{Precision} = \frac{\text{true positives}} {\text{true positives} + \text{false positives}}$$

où :

• Un vrai positif signifie que le modèle a prédit correctement la classe positive.
• Un faux positif signifie que le modèle a prédit à tort la classe positive.

Par exemple, supposons qu'un modèle a effectué 200 prédictions positives. Parmi ces 200 prédictions positives :

• 150 étaient des vrais positifs.
• 50 étaient des faux positifs.

Dans ce cas :

$$\text{Precision} = \frac{\text{150}} {\text{150} + \text{50}} = 0.75$$

À comparer à la justesse et au rappel.

Pour en savoir plus, consultez Classification : précision, rappel, exactitude et métriques associées dans le Cours d'initiation au Machine Learning.

prédiction

#fundamentals

Résultat d'un modèle. Exemple :

• La prédiction d'un modèle de classification binaire correspond à la classe positive ou à la classe négative.
• La prédiction d'un modèle de classification à classes multiples est une classe.
• La prédiction d'un modèle de régression linéaire est un nombre.

étiquettes de substitution

#fundamentals

Données utilisées pour réaliser une approximation des libellés qui ne sont pas directement disponibles dans un ensemble de données.

Par exemple, supposons que vous deviez entraîner un modèle pour prédire le niveau de stress des employés. Votre ensemble de données contient de nombreuses caractéristiques prédictives, mais pas d'étiquette nommée niveau de stress. Sans vous décourager, vous choisissez "accidents du travail" comme libellé proxy pour le niveau de stress. En effet, les employés stressés sont plus susceptibles d'avoir des accidents que les employés calmes. Ou pas ? Il est possible que les accidents du travail augmentent et diminuent pour plusieurs raisons.

Prenons un deuxième exemple. Supposons que vous souhaitiez que pleut-il ? soit une étiquette booléenne pour votre ensemble de données, mais que celui-ci ne contienne pas de données sur la pluie. Si des photos sont disponibles, vous pouvez créer des photos de personnes portant des parapluies comme étiquette de substitution pour la phrase is it raining? Est-ce un bon libellé de substitution ? C'est possible, mais dans certaines cultures, les gens sont plus susceptibles de porter un parapluie pour se protéger du soleil que de la pluie.

Les libellés de substitution sont souvent imparfaits. Dans la mesure du possible, choisissez des libellés réels plutôt que des libellés de substitution. Cela dit, en l'absence d'étiquette réelle, choisissez l'étiquette de substitution avec beaucoup de soin, en sélectionnant le candidat le moins horrible.

Pour en savoir plus, consultez Ensembles de données : libellés dans le Cours d'initiation au Machine Learning.

R

RAG

#fundamentals

Abréviation de génération augmentée par récupération.

évaluateur

#fundamentals

Personne qui fournit des libellés pour des exemples. "Annotateur" est un autre nom pour évaluateur.

Pour en savoir plus, consultez Données catégorielles : problèmes courants dans le Cours d'initiation au Machine Learning.

recall (rappel)

#fundamentals

#Metric

Statistique des modèles de classification qui répond à la question suivante :

Lorsque la vérité terrain correspondait à la classe positive, quel pourcentage de prédictions le modèle a-t-il correctement identifié comme classe positive ?

Voici la formule :

\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]

où :

• Un vrai positif signifie que le modèle a prédit correctement la classe positive.
• Un faux négatif signifie que le modèle a prédit à tort la classe négative.

Par exemple, supposons que votre modèle ait effectué 200 prédictions sur des exemples pour lesquels la vérité terrain était la classe positive. Sur ces 200 prédictions :

• 180 étaient des vrais positifs.
• 20 étaient des faux négatifs.

Dans ce cas :

\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]

Cliquez sur l'icône pour afficher des notes sur les ensembles de données avec déséquilibre des classes.

Le rappel est particulièrement utile pour déterminer le pouvoir prédictif des modèles de classification dans lesquels la classe positive est rare. Prenons l'exemple d'un ensemble de données déséquilibré dans lequel la classe positive pour une certaine maladie ne se produit que chez 10 patients sur un million. Supposons que votre modèle effectue cinq millions de prédictions qui donnent les résultats suivants :

• 30 vrais positifs
• 20 faux négatifs
• 4 999 000 vrais négatifs
• 950 faux positifs

Le rappel de ce modèle est donc le suivant :

recall = TP / (TP + FN)
recall = 30 / (30 + 20) = 0.6 = 60%

En revanche, la précision de ce modèle est la suivante :

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (30 + 4,999,000) / (30 + 4,999,000 + 950 + 20) = 99.98%

Cette valeur de précision élevée semble impressionnante, mais elle n'a en réalité aucune signification. Le rappel est une métrique beaucoup plus utile que la précision pour les ensembles de données avec déséquilibre des classes.

---

Pour en savoir plus, consultez Classification : précision, rappel et métriques associées.

Unité de rectification linéaire (ReLU)

#fundamentals

Fonction d'activation dont le comportement est le suivant :

• Si l'entrée est négative ou nulle, la sortie est 0.
• Si l'entrée est positive, la sortie est égale à l'entrée.

Exemple :

• Si l'entrée est -3, la sortie est 0.
• Si l'entrée est +3, la sortie est 3.0.

Voici un graphique de ReLU :

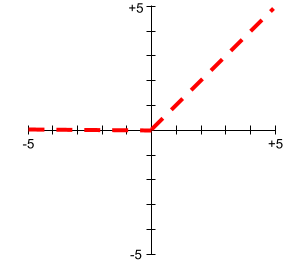
ReLU est une fonction d'activation très populaire. Malgré son comportement simple, ReLU permet toujours à un réseau de neurones d'apprendre les relations non linéaires entre les caractéristiques et le libellé.

modèle de régression

#fundamentals

Informellement, un modèle qui génère une prédiction numérique. (À l'inverse, un modèle de classification génère une prédiction de classe.) Par exemple, les modèles suivants sont tous des modèles de régression :

• Un modèle qui prédit la valeur d'une maison en euros, par exemple 423 000.
• Modèle qui prédit l'espérance de vie d'un arbre en années, par exemple 23,2.
• Modèle qui prédit la quantité de pluie (en centimètres) qui tombera dans une ville donnée au cours des six prochaines heures, par exemple 0,46 cm.

Voici deux types courants de modèles de régression :

• La régression linéaire, qui trouve la ligne qui correspond le mieux aux valeurs de libellé par rapport aux caractéristiques.
• La régression logistique, qui génère une probabilité comprise entre 0,0 et 1,0 qu'un système mappe généralement à une prédiction de classe.

Tous les modèles qui génèrent des prédictions numériques ne sont pas des modèles de régression. Dans certains cas, une prédiction numérique n'est en réalité qu'un modèle de classification dont les noms de classes sont numériques. Par exemple, un modèle qui prédit un code postal numérique est un modèle de classification, et non un modèle de régression.

régularisation

#fundamentals

Tout mécanisme qui réduit le surapprentissage. Voici quelques types de régularisation courants :

• Régularisation L₁
• Régularisation L₂
• Régularisation par abandon
• Arrêt prématuré (Il ne s'agit pas vraiment d'une méthode de régularisation, mais l'arrêt prématuré peut limiter efficacement le surapprentissage.)

La régularisation peut également être définie comme la pénalité appliquée à la complexité d'un modèle.

Cliquez sur l'icône pour afficher des notes supplémentaires.

La régularisation est contre-intuitive. L'augmentation de la régularisation augmente généralement la perte d'entraînement, ce qui est déroutant, car l'objectif n'est-il pas de minimiser la perte d'entraînement ?

En fait, non. L'objectif n'est pas de minimiser la perte d'entraînement. L'objectif est de faire d'excellentes prédictions sur des exemples concrets. Étonnamment, même si l'augmentation de la régularisation accroît la perte d'entraînement, elle aide généralement les modèles à faire de meilleures prédictions sur des exemples concrets.

---

Pour en savoir plus, consultez Surapprentissage : complexité du modèle dans le Cours d'initiation au Machine Learning.

taux de régularisation

#fundamentals

Nombre qui spécifie l'importance relative de la régularisation pendant l'entraînement. L'augmentation du taux de régularisation réduit le surapprentissage, mais peut réduire le pouvoir prédictif du modèle. À l'inverse, réduire ou omettre le taux de régularisation augmente le surapprentissage.

Cliquez sur l'icône pour afficher le calcul.

Le taux de régularisation est généralement représenté par la lettre grecque lambda. L'équation de perte simplifiée suivante montre l'influence de lambda :

$$\text{minimize(loss function + }\lambda\text{(regularization))}$$

où regularization est un mécanisme de régularisation, y compris :

• Régularisation L₁
• Régularisation L₂

---

Pour en savoir plus, consultez Surapprentissage : régularisation L2 dans le cours d'initiation au machine learning.

ReLU

#fundamentals

Abréviation de Rectified Linear Unit.

génération augmentée par récupération (RAG)

#fundamentals

Technique permettant d'améliorer la qualité de la sortie d'un grand modèle de langage (LLM) en l'ancrant avec des sources de connaissances récupérées après l'entraînement du modèle. Le RAG améliore la précision des réponses des LLM en leur donnant accès à des informations extraites de bases de connaissances ou de documents fiables.

Voici quelques raisons courantes d'utiliser la génération augmentée par récupération :

• Améliorer la justesse factuelle des réponses générées par un modèle.
• Donner au modèle l'accès à des connaissances sur lesquelles il n'a pas été entraîné.
• Modifier les connaissances utilisées par le modèle.
• Permettre au modèle de citer des sources.

Par exemple, supposons qu'une application de chimie utilise l'API PaLM pour générer des résumés liés aux requêtes des utilisateurs. Lorsque le backend de l'application reçoit une requête, il effectue les opérations suivantes :

1. Recherche ("récupère") les données pertinentes pour la requête de l'utilisateur.
2. Ajoute ("augmente") les données de chimie pertinentes à la requête de l'utilisateur.
3. Indique au LLM de créer un résumé en fonction des données ajoutées.

Courbe ROC (receiver operating characteristic)

#fundamentals

#Metric

Graphique du taux de vrais positifs par rapport au taux de faux positifs pour différents seuils de classification dans la classification binaire.

La forme d'une courbe ROC suggère la capacité d'un modèle de classification binaire à séparer les classes positives des classes négatives. Supposons, par exemple, qu'un modèle de classification binaire sépare parfaitement toutes les classes négatives de toutes les classes positives :

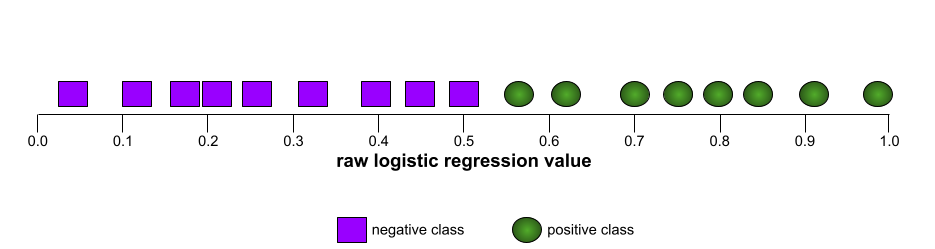
La courbe ROC du modèle précédent se présente comme suit :

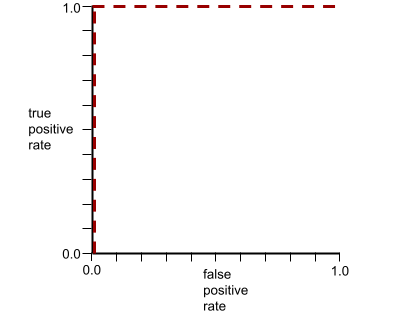
En revanche, l'illustration suivante représente les valeurs brutes de régression logistique pour un modèle médiocre qui ne peut pas du tout séparer les classes négatives des classes positives :

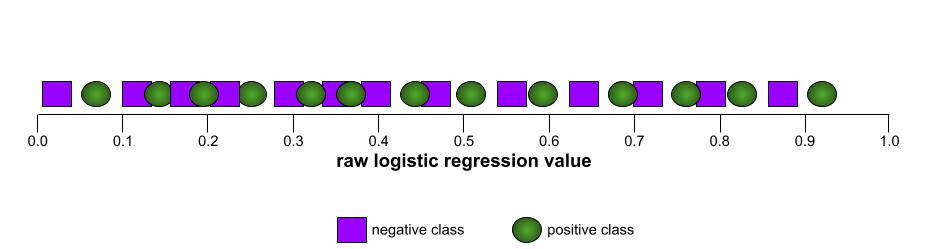
La courbe ROC de ce modèle se présente comme suit :

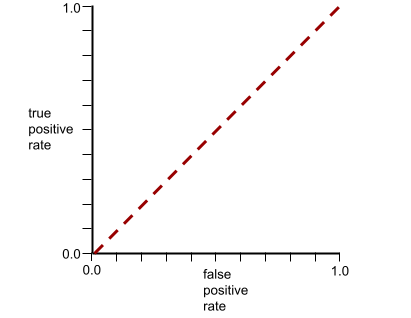
Dans le monde réel, la plupart des modèles de classification binaire séparent les classes positives et négatives dans une certaine mesure, mais généralement pas parfaitement. Par conséquent, une courbe ROC typique se situe quelque part entre les deux extrêmes :

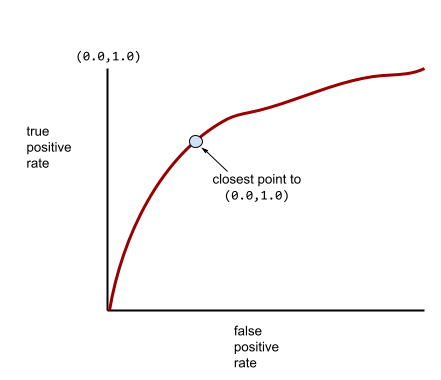
Le point d'une courbe ROC le plus proche de (0.0,1.0) identifie théoriquement le seuil de classification idéal. Toutefois, plusieurs autres problèmes concrets influencent la sélection du seuil de classification idéal. Par exemple, les faux négatifs peuvent être beaucoup plus problématiques que les faux positifs.

Une métrique numérique appelée AUC résume la courbe ROC en une seule valeur à virgule flottante.

la racine carrée de l'erreur quadratique moyenne (RMSE, Root Mean Squared Error)

#fundamentals

#Metric

Racine carrée de l'erreur quadratique moyenne.

S

fonction sigmoïde

#fundamentals

Fonction mathématique qui "écrase" une valeur d'entrée dans une plage limitée, généralement de 0 à 1 ou de -1 à +1. Autrement dit, vous pouvez transmettre n'importe quel nombre (deux, un million, un milliard négatif, etc.) à une sigmoïde, et la sortie sera toujours dans la plage contrainte. Voici à quoi ressemble un graphique de la fonction d'activation sigmoïde :

La fonction sigmoïde a plusieurs utilisations dans le machine learning, y compris :

• Conversion de la sortie brute d'un modèle de régression logistique ou de régression multinomiale en probabilité.
• Agit comme une fonction d'activation dans certains réseaux de neurones.

Cliquez sur l'icône pour afficher le calcul.

La fonction sigmoïde pour un nombre d'entrée x a la formule suivante :

$$ sigmoid(x) = \frac{1}{1 + e^{-\text{x}}} $$

En machine learning, x est généralement une somme pondérée.

---

softmax

#fundamentals

Fonction qui détermine les probabilités pour chaque classe possible dans un modèle de classification à classes multiples. La somme des probabilités est exactement égale à 1.0. Par exemple, le tableau suivant montre comment softmax distribue différentes probabilités :

L'image est…	Probabilité
chien	0,85
cat	.13
cheval	.02

Softmax est également appelé softmax complet.

À comparer à l'échantillonnage de candidats.

Cliquez sur l'icône pour afficher le calcul.

L'équation softmax est la suivante :

$$\sigma_i = \frac{e^{\text{z}_i}} {\sum_{j=1}^{j=K} {e^{\text{z}_j}}} $$

où :

• $\sigma_i$ est le vecteur de sortie. Chaque élément du vecteur de sortie spécifie la probabilité de cet élément. La somme de tous les éléments du vecteur de sortie est égale à 1.0. Le vecteur de sortie contient le même nombre d'éléments que le vecteur d'entrée $z$.
• $z$ est le vecteur d'entrée. Chaque élément du vecteur d'entrée contient une valeur à virgule flottante.
• $K$ correspond au nombre d'éléments dans le vecteur d'entrée (et le vecteur de sortie).

Par exemple, supposons que le vecteur d'entrée soit le suivant :

[1.2, 2.5, 1.8]

Softmax calcule donc le dénominateur comme suit :

$$\text{denominator} = e^{1.2} + e^{2.5} + e^{1.8} = 21.552$$

La probabilité softmax de chaque élément est donc la suivante :

$$\sigma_1 = \frac{e^{1.2}}{21.552} = 0.154 $$ $$\sigma_2 = \frac{e^{2.5}}{21.552} = 0.565 $$ $$\sigma_1 = \frac{e^{1.8}}{21.552} = 0.281 $$

Le vecteur de sortie est donc le suivant :

$$\sigma = [0.154, 0.565, 0.281]$$

La somme des trois éléments de $\sigma$ est égale à 1. Ouf !

---

Pour en savoir plus, consultez Réseaux de neurones : classification multiclasse dans le cours d'initiation au machine learning.

caractéristique creuse

#fundamentals

Caractéristique dont les valeurs sont pour la plupart nulles ou vides. Par exemple, une caractéristique contenant une seule valeur 1 et un million de valeurs 0 est considérée comme éparse. En revanche, une caractéristique dense comporte des valeurs qui ne sont pas majoritairement nulles ni vides.

En machine learning, un nombre surprenant de caractéristiques sont des caractéristiques éparses. Les caractéristiques catégorielles sont généralement des caractéristiques éparses. Par exemple, sur les 300 espèces d'arbres possibles dans une forêt, un seul exemple peut identifier un érable. Ou, parmi les millions de vidéos possibles dans une bibliothèque vidéo, un seul exemple peut identifier "Casablanca".

Dans un modèle, vous représentez généralement les caractéristiques creuses avec l'encodage one-hot. Si l'encodage one-hot est volumineux, vous pouvez ajouter une couche d'embedding au-dessus de l'encodage one-hot pour plus d'efficacité.

représentation creuse

#fundamentals

Stockage uniquement des positions des éléments non nuls dans une caractéristique éparse.

Par exemple, supposons qu'une caractéristique catégorielle nommée species identifie les 36 espèces d'arbres d'une forêt donnée. Supposons également que chaque exemple n'identifie qu'une seule espèce.

Vous pouvez utiliser un vecteur one-hot pour représenter les espèces d'arbres dans chaque exemple. Un vecteur one-hot contiendrait un seul 1 (pour représenter l'espèce d'arbre spécifique dans cet exemple) et 35 0 (pour représenter les 35 espèces d'arbres non présentes dans cet exemple). La représentation one-hot de maple peut donc ressembler à ce qui suit :

Une représentation creuse identifierait simplement la position de l'espèce en question. Si maple se trouve à la position 24, la représentation creuse de maple serait simplement la suivante :

24

Notez que la représentation creuse est beaucoup plus compacte que la représentation one-hot.

Remarque : Vous ne devez pas transmettre de représentation creuse en tant qu'entrée de caractéristique directe à un modèle. Au lieu de cela, vous devez convertir la représentation creuse en représentation one-hot avant de l'utiliser pour l'entraînement.

Cliquez sur l'icône pour obtenir un exemple légèrement plus complexe.

Supposons que chaque exemple de votre modèle doive représenter les mots d'une phrase en anglais, mais pas leur ordre. L'anglais se compose d'environ 170 000 mots. Il s'agit donc d'une caractéristique catégorielle avec environ 170 000 éléments. La plupart des phrases en anglais utilisent une infime fraction de ces 170 000 mots. L'ensemble de mots dans un seul exemple sera donc presque certainement une donnée creuse.

Considérez la phrase suivante :

My dog is a great dog

Vous pouvez utiliser une variante de vecteur one-hot pour représenter les mots de cette phrase. Dans cette variante, plusieurs cellules du vecteur peuvent contenir une valeur non nulle. De plus, dans cette variante, une cellule peut contenir un nombre entier autre que un. Bien que les mots "mon", "est", "un" et "super" n'apparaissent qu'une seule fois dans la phrase, le mot "chien" apparaît deux fois. L'utilisation de cette variante de vecteurs one-hot pour représenter les mots de cette phrase donne le vecteur de 170 000 éléments suivant :

Une représentation creuse de la même phrase serait simplement :

0: 1
26100: 2
45770: 1
58906: 1
91520: 1

---

Cliquez sur l'icône si vous êtes perdu.

Le terme "représentation creuse" en déroute plus d'un, car une représentation creuse n'est pas un vecteur creux. En réalité, la représentation creuse est une représentation dense d'un vecteur creux. La représentation d'index des synonymes est un peu plus claire que "représentation creuse".

---

Pour en savoir plus, consultez Utiliser des données catégorielles dans le Cours d'initiation au Machine Learning.

vecteur creux

#fundamentals

Vecteur dont les valeurs sont principalement nulles. Voir aussi caractéristique creuse et creux.

perte quadratique

#fundamentals

#Metric

Synonyme de perte _L2.

static

#fundamentals

Action ponctuelle et non continue. Les termes statique et hors connexion sont synonymes. Voici des utilisations courantes des termes statique et hors connexion dans le machine learning :

• Un modèle statique (ou modèle hors connexion) est un modèle entraîné une seule fois, puis utilisé pendant un certain temps.
• L'entraînement statique (ou entraînement hors connexion) est le processus d'entraînement d'un modèle statique.
• L'inférence statique (ou inférence hors connexion) est un processus dans lequel un modèle génère un lot de prédictions à la fois.

À comparer à dynamique.

inférence statique

#fundamentals

Synonyme d'inférence hors connexion.

stationnarité

#fundamentals

Caractéristique dont les valeurs ne changent pas pour une ou plusieurs dimensions, généralement le temps. Par exemple, une caractéristique dont les valeurs sont à peu près les mêmes en 2021 et en 2023 présente une stationnarité.

Dans la réalité, très peu de caractéristiques présentent une stationnarité. Même les caractéristiques synonymes de stabilité (comme le niveau de la mer) évoluent au fil du temps.

À comparer à la non-stationnarité.

descente de gradient stochastique (SGD)

#fundamentals

Algorithme de descente de gradient dans lequel la taille de lot est égale à un. Autrement dit, la descente de gradient stochastique s'entraîne sur un seul exemple prélevé uniformément, de manière aléatoire, dans un ensemble d'entraînement.

Pour en savoir plus, consultez Régression linéaire : hyperparamètres dans le Cours d'initiation au Machine Learning.

machine learning supervisé

#fundamentals

Entraînement d'un modèle à partir de caractéristiques et de leurs libellés correspondants. Le machine learning supervisé est comparable à l'apprentissage d'un sujet en étudiant une série de questions et les réponses correspondantes. Après avoir maîtrisé la mise en correspondance entre les questions et les réponses, un élève peut ensuite répondre à de nouvelles questions (jamais vues auparavant) sur le même sujet.

À comparer au machine learning non supervisé.

Pour en savoir plus, consultez la section Apprentissage supervisé du cours "Introduction au ML".

caractéristique synthétique

#fundamentals

Une caractéristique absente des caractéristiques d'entrée, mais assemblée à partir d'une ou plusieurs d'entre elles. Voici quelques méthodes pour créer des caractéristiques synthétiques :

• Binning d'une caractéristique continue dans des paquets de plage
• Création d'un croisement de caractéristiques
• Multiplication (ou division) d'une valeur de caractéristique par d'autres valeurs de caractéristiques ou par elle-même Par exemple, si a et b sont des caractéristiques d'entrée, les exemples suivants sont des caractéristiques synthétiques :
  • ab
  • a²
• Appliquer une fonction transcendante à une valeur de caractéristique. Par exemple, si c est une caractéristique d'entrée, les exemples suivants sont des caractéristiques synthétiques :
  • sin(c)
  • ln(c)

Les caractéristiques créées par normalisation ou mise à l'échelle ne sont pas considérées comme des caractéristiques synthétiques.

T

perte de test

#fundamentals

#Metric

Une métrique représentant la perte d'un modèle par rapport à l'ensemble de test. Lorsque vous créez un modèle, vous essayez généralement de minimiser la perte de test. En effet, une faible perte de test est un signal de qualité plus fort qu'une faible perte d'entraînement ou une faible perte de validation.

Un écart important entre la perte de test et la perte d'entraînement ou de validation suggère parfois que vous devez augmenter le taux de régularisation.

entraînement

#fundamentals

Processus consistant à déterminer les paramètres (pondérations et biais) idéaux d'un modèle. Lors de l'entraînement, un système lit des exemples et ajuste progressivement les paramètres. L'entraînement utilise chaque exemple de quelques fois à des milliards de fois.

Pour en savoir plus, consultez la section Apprentissage supervisé du cours "Introduction au ML".

perte d'entraînement

#fundamentals

#Metric

Métrique représentant la perte d'un modèle lors d'une itération d'entraînement spécifique. Par exemple, supposons que la fonction de perte soit Mean Squared Error. Supposons que la perte d'entraînement (erreur quadratique moyenne) pour la 10e itération soit de 2,2 et que la perte d'entraînement pour la 100e itération soit de 1,9.

Une courbe de perte représente la perte d'entraînement par rapport au nombre d'itérations. Une courbe de perte fournit les indications suivantes sur l'entraînement :

• Une pente descendante implique que le modèle s'améliore.
• Une pente ascendante signifie que le modèle se dégrade.
• Une pente plate signifie que le modèle a atteint la convergence.

Par exemple, la courbe de perte suivante, quelque peu idéalisée, montre :

• Une pente descendante abrupte lors des itérations initiales, ce qui implique une amélioration rapide du modèle.
• Une pente qui s'aplatit progressivement (mais reste descendante) jusqu'à la fin de l'entraînement, ce qui implique une amélioration continue du modèle à un rythme un peu plus lent que lors des itérations initiales.
• Une pente plate vers la fin de l'entraînement, ce qui suggère une convergence.

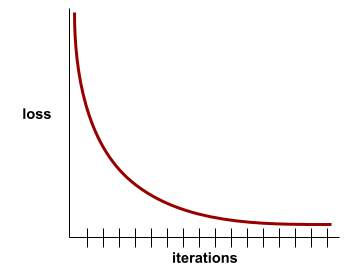
Bien que la perte d'entraînement soit importante, consultez également la section Généralisation.

décalage entraînement/mise en service

#fundamentals

La différence entre les performances d'un modèle pendant l'entraînement et celles du même modèle pendant la diffusion.

ensemble d'entraînement

#fundamentals

Sous-ensemble de l'ensemble de données utilisé pour entraîner un modèle.

Traditionnellement, les exemples de l'ensemble de données sont divisés en trois sous-ensembles distincts :

• un ensemble d'entraînement ;
• un ensemble de validation.
• un ensemble de test ;

Idéalement, chaque exemple de l'ensemble de données ne doit appartenir qu'à l'un des sous-ensembles précédents. Par exemple, un même exemple ne doit pas appartenir à la fois à l'ensemble d'entraînement et à l'ensemble de validation.

Pour en savoir plus, consultez Ensembles de données : diviser l'ensemble de données d'origine dans le cours d'initiation au machine learning.

vrai négatif (VN)

#fundamentals

#Metric

Exemple dans lequel le modèle prédit correctement la classe négative. Par exemple, le modèle déduit qu'un e-mail particulier n'est pas du spam, ce qui est bien le cas.

vrai positif (VP)

#fundamentals

#Metric

Exemple dans lequel le modèle prédit correctement la classe positive. Par exemple, le modèle déduit qu'un e-mail particulier est du spam, ce qui est bien le cas.

taux de vrais positifs (TVP)

#fundamentals

#Metric

Synonyme de rappel. Par exemple :

$$\text{true positive rate} = \frac {\text{true positives}} {\text{true positives} + \text{false negatives}}$$

Le taux de vrais positifs correspond à l'ordonnée d'une courbe ROC.

U

sous-ajustement

#fundamentals

Produire un modèle qui a une faible capacité de prédiction, car le modèle n'a pas appréhendé la complexité des données d'entraînement. De nombreux problèmes peuvent causer un sous-apprentissage, y compris :

• Entraînement sur un ensemble de caractéristiques inadéquat
• Entraînement sur trop peu d'époques ou avec un taux d'apprentissage trop faible.
• Entraînement avec un taux de régularisation trop élevé.
• Fournir trop peu de couches cachées dans un réseau de neurones profond

Pour en savoir plus, consultez Surapprentissage dans le Cours d'initiation au Machine Learning.

exemple sans étiquette

#fundamentals

Exemple contenant des caractéristiques, mais aucune étiquette. Par exemple, le tableau suivant présente trois exemples non étiquetés issus d'un modèle d'évaluation de maisons, chacun comportant trois caractéristiques, mais aucune valeur de maison :

Nombre de chambres	Nombre de salles de bain	Âge de la maison
3	2	15
2	1	72
4	2	34

Dans le machine learning supervisé, les modèles sont entraînés sur des exemples étiquetés et effectuent des prédictions sur des exemples sans étiquette.

Dans l'apprentissage semi-supervisé et non supervisé, les exemples sans étiquette sont utilisés pendant l'entraînement.

À comparer à un exemple étiqueté.

machine learning non supervisé

#clustering

#fundamentals

Entraînement d'un modèle pour détecter des schémas dans un ensemble de données, généralement sans étiquette.

Le machine learning non supervisé est surtout utilisé pour regrouper les données dans des groupes d'exemples similaires. Par exemple, un algorithme d'apprentissage automatique non supervisé peut regrouper des titres en fonction de diverses propriétés de la musique. Les clusters obtenus peuvent servir d'entrée à d'autres algorithmes de machine learning (par exemple, à un service de recommandation musicale). Le clustering peut être utile lorsque les libellés utiles sont rares ou absents. Par exemple, dans les domaines tels que la lutte contre les abus et la fraude, les clusters peuvent aider à mieux comprendre les données.

À comparer au machine learning supervisé.

Cliquez sur l'icône pour afficher des notes supplémentaires.

Un autre exemple de machine learning non supervisé est l'analyse en composantes principales (ACP). Par exemple, l'application de la PCA sur un ensemble de données contenant des millions de paniers d'achat peut révéler que ceux contenant des citrons contiennent également fréquemment des antiacides.

---

Pour en savoir plus, consultez Qu'est-ce que le machine learning ? dans le cours d'introduction au ML.

V

validation

#fundamentals

Évaluation initiale de la qualité d'un modèle. La validation vérifie la qualité des prédictions d'un modèle par rapport à l'ensemble de validation.

Étant donné que l'ensemble de validation diffère de l'ensemble d'entraînement, la validation permet de se prémunir contre le surapprentissage.

Vous pouvez considérer l'évaluation du modèle par rapport à l'ensemble de validation comme le premier cycle de test et l'évaluation du modèle par rapport à l'ensemble de test comme le deuxième cycle de test.

perte de validation

#fundamentals

#Metric

Métrique représentant la perte d'un modèle sur l'ensemble de validation lors d'une itération d'entraînement spécifique.

Voir aussi courbe de généralisation.

ensemble de validation

#fundamentals

Sous-ensemble de l'ensemble de données qui effectue une évaluation initiale par rapport à un modèle entraîné. En règle générale, vous évaluez le modèle entraîné par rapport à l'ensemble de validation plusieurs fois avant de l'évaluer par rapport à l'ensemble de test.

Traditionnellement, vous divisez les exemples de l'ensemble de données en trois sous-ensembles distincts :

• un ensemble d'entraînement
• un ensemble de validation ;
• un ensemble de test ;

Idéalement, chaque exemple de l'ensemble de données ne doit appartenir qu'à l'un des sous-ensembles précédents. Par exemple, un même exemple ne doit pas appartenir à la fois à l'ensemble d'entraînement et à l'ensemble de validation.

Pour en savoir plus, consultez Ensembles de données : diviser l'ensemble de données d'origine dans le cours d'initiation au machine learning.

W

weight

#fundamentals

Valeur par laquelle un modèle multiplie une autre valeur. L'entraînement est le processus qui permet de déterminer les pondérations idéales d'un modèle. L'inférence est le processus qui permet d'utiliser ces pondérations apprises pour faire des prédictions.

Cliquez sur l'icône pour voir un exemple de pondérations dans un modèle linéaire.

Imaginez un modèle linéaire avec deux caractéristiques. Supposons que l'entraînement détermine les pondérations (et le biais) suivants :

• Le biais, b, a une valeur de 2,2.
• Le poids w₁ associé à une caractéristique est de 1, 5.
• Le poids w₂ associé à l'autre caractéristique est de 0, 4.

Imaginons maintenant un exemple avec les valeurs de caractéristiques suivantes :

• La valeur d'une caractéristique, x₁, est de 6.
• La valeur de l'autre caractéristique, x₂, est de 10.

Ce modèle linéaire utilise la formule suivante pour générer une prédiction, y' :

$$y' = b + w_1x_1 + w_2x_2$$

La prédiction est donc la suivante :

$$y' = 2.2 + (1.5)(6) + (0.4)(10) = 15.2$$

Si la pondération est égale à 0, la caractéristique correspondante ne contribue pas au modèle. Par exemple, si w₁ est égal à 0, la valeur de x₁ n'a pas d'importance.

---

Pour en savoir plus, consultez Régression linéaire dans le Cours d'initiation au Machine Learning.

Somme pondérée

#fundamentals

Somme de toutes les valeurs d'entrée pertinentes multipliées par leurs pondérations correspondantes. Par exemple, supposons que les entrées pertinentes sont les suivantes :

valeur d'entrée	pondération d'entrée
2	-1,3
-1	0,6
3	0,4

La somme pondérée est donc la suivante :

weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0

Une somme pondérée est l'argument d'entrée d'une fonction d'activation.

Z

Normalisation du score Z

#fundamentals

Technique de scaling qui remplace une valeur feature brute par une valeur à virgule flottante représentant le nombre d'écarts-types par rapport à la moyenne de cette feature. Prenons l'exemple d'une caractéristique dont la moyenne est de 800 et dont l'écart-type est de 100. Le tableau suivant montre comment la normalisation du score Z mapperait la valeur brute à son score Z :

Valeur brute	Cote Z
800	0
950	+1,5
575	-2,25

Le modèle de machine learning s'entraîne ensuite sur les scores Z de cette caractéristique au lieu des valeurs brutes.

Pour en savoir plus, consultez Données numériques : normalisation dans le Cours d'initiation au machine learning.