อภิธานศัพท์แมชชีนเลิร์นนิง: เมตริก

หน้านี้มีคําศัพท์ในอภิธานศัพท์เกี่ยวกับเมตริก ดูคำศัพท์ทั้งหมดในอภิธานศัพท์ได้โดยการคลิกที่นี่

A

ความแม่นยำ

#fundamentals

#Metric

จํานวนการคาดการณ์การจัดประเภทที่ถูกต้องหารด้วยจํานวนการคาดการณ์ทั้งหมด โดยการ

$$\text{Accuracy} = \frac{\text{correct predictions}} {\text{correct predictions + incorrect predictions }}$$

ตัวอย่างเช่น โมเดลที่ทําการคาดการณ์ที่ถูกต้อง 40 ครั้งและการคาดการณ์ที่ไม่ถูกต้อง 10 ครั้งจะมีความแม่นยําเท่ากับ

$$\text{Accuracy} = \frac{\text{40}} {\text{40 + 10}} = \text{80%}$$

การจัดประเภทแบบไบนารีจะตั้งชื่อเฉพาะสำหรับการคาดการณ์ที่ถูกต้องและการคาดการณ์ที่ไม่ถูกต้องในหมวดหมู่ต่างๆ ดังนั้น สูตรความแม่นยำสำหรับการจัดประเภทแบบไบนารีจึงมีดังนี้

$$\text{Accuracy} = \frac{\text{TP} + \text{TN}} {\text{TP} + \text{TN} + \text{FP} + \text{FN}}$$

where:

• TP คือจํานวนผลบวกจริง (การคาดการณ์ที่ถูกต้อง)
• TN คือจํานวนผลลบจริง (การคาดการณ์ที่ถูกต้อง)
• FP คือจํานวนผลบวกลวง (การคาดการณ์ที่ไม่ถูกต้อง)
• FN คือจํานวนผลลบเท็จ (การคาดการณ์ที่ไม่ถูกต้อง)

เปรียบเทียบความถูกต้องกับความแม่นยำและความแม่นยำในการจดจำ

คลิกไอคอนเพื่อดูรายละเอียดเกี่ยวกับความแม่นยำและชุดข้อมูลที่มีจำนวนของคลาสไม่สมดุล

แม้ว่าความถูกต้องจะเป็นเมตริกที่มีคุณค่าในบางสถานการณ์ แต่อาจทําให้เข้าใจผิดอย่างมากในบางสถานการณ์ โปรดทราบว่าความแม่นยำมักเป็นเมตริกที่ไม่ดีสำหรับการประเมินโมเดลการจัดประเภทที่ประมวลผลชุดข้อมูลที่มีจำนวนตัวอย่างไม่สมดุล

ตัวอย่างเช่น สมมติว่าหิมะตกเพียง 25 วันต่อศตวรรษในเมืองเขตร้อน เนื่องจากวันที่ไม่มีหิมะ (คลาสเชิงลบ) มีอยู่เป็นจำนวนมากกว่าวันที่มีหิมะ (คลาสเชิงบวก) ชุดข้อมูลหิมะของเมืองนี้จึงมีความไม่สมดุลของคลาส ลองจินตนาการถึงโมเดลการจัดประเภทแบบไบนารีที่ควรจะคาดการณ์ว่าจะมีหิมะหรือไม่มีหิมะในแต่ละวัน แต่กลับคาดการณ์ว่า "ไม่มีหิมะ" ทุกวัน โมเดลนี้มีความแม่นยำสูงแต่ไม่มีความสามารถในการคาดการณ์ ตารางต่อไปนี้สรุปผลลัพธ์ของการคาดการณ์ตลอด 1 ศตวรรษ

หมวดหมู่	ตัวเลข
TP	0
TN	36499
FP	0
FN	25

ดังนั้นความแม่นยำของโมเดลนี้คือ

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (0 + 36499) / (0 + 36499 + 0 + 25) = 0.9993 = 99.93%

แม้ว่าความแม่นยำ 99.93% จะดูเหมือนเป็นเปอร์เซ็นต์ที่น่าประทับใจมาก แต่โมเดลนี้ไม่มีความสามารถในการคาดการณ์

ความแม่นยำและความไวในการรับสัญญาณมักเป็นเมตริกที่มีประโยชน์มากกว่าความถูกต้องในการประเมินโมเดลที่ฝึกในชุดข้อมูลที่มีคลาสไม่สมดุล

---

ดูข้อมูลเพิ่มเติมได้ในการจัดประเภท: ความแม่นยำ การเรียกคืน ความแม่นยำ และเมตริกที่เกี่ยวข้องในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง

พื้นที่ใต้กราฟ PR

#Metric

ดูPR AUC (พื้นที่ใต้กราฟ PR)

พื้นที่ใต้เส้นโค้ง ROC

#Metric

ดู AUC (พื้นที่ใต้กราฟ ROC)

AUC (พื้นที่ใต้เส้นโค้ง ROC)

#fundamentals

#Metric

ตัวเลขระหว่าง 0.0 ถึง 1.0 ที่แสดงถึงความสามารถของโมเดลการจัดประเภทแบบไบนารีในการแยกคลาสที่เป็นบวกออกจากคลาสที่เป็นลบ ยิ่ง AUC ใกล้เคียงกับ 1.0 มากเท่าใด ความสามารถในการแยกคลาสออกจากกันของโมเดลก็จะยิ่งดีขึ้นเท่านั้น

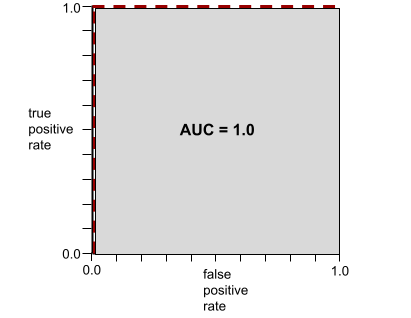
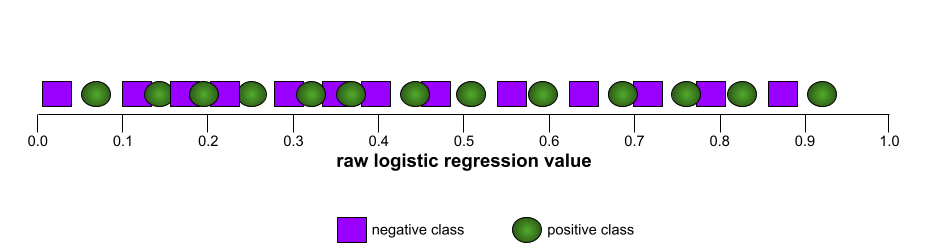
ตัวอย่างเช่น ภาพต่อไปนี้แสดงโมเดลการจัดประเภทที่แยกคลาสที่เป็นบวก (รูปไข่สีเขียว) ออกจากคลาสที่เป็นลบ (สี่เหลี่ยมผืนผ้าสีม่วง) อย่างสมบูรณ์ โมเดลที่สมบูรณ์แบบเกินจริงนี้มีค่า AUC เท่ากับ 1.0

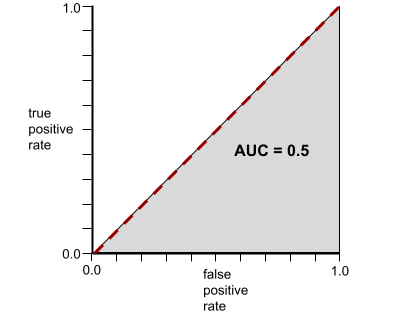
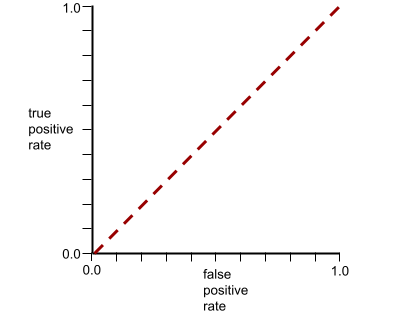
ในทางกลับกัน ภาพต่อไปนี้แสดงผลลัพธ์ของโมเดลการจัดประเภทที่สร้างผลลัพธ์แบบสุ่ม โมเดลนี้มีค่า AUC เท่ากับ 0.5

ใช่ โมเดลก่อนหน้ามี AUC เท่ากับ 0.5 ไม่ใช่ 0.0

โมเดลส่วนใหญ่อยู่ตรงกลางระหว่าง 2 รูปแบบข้างต้น ตัวอย่างเช่น โมเดลต่อไปนี้แยกรายการเชิงบวกออกจากรายการเชิงลบได้บ้าง จึงมี AUC อยู่ระหว่าง 0.5 ถึง 1.0

AUC จะไม่สนใจค่าที่คุณตั้งไว้สําหรับเกณฑ์การจัดประเภท แต่ AUC จะพิจารณาเกณฑ์การจัดประเภทที่เป็นไปได้ทั้งหมดแทน

คลิกไอคอนเพื่อดูข้อมูลเกี่ยวกับความสัมพันธ์ระหว่าง AUC กับเส้นโค้ง ROC

AUC แสดงถึงพื้นที่ใต้กราฟ ROC ตัวอย่างเช่น กราฟ ROC ของโมเดลที่แยกผลบวกออกจากผลลบได้อย่างสมบูรณ์จะมีลักษณะดังนี้

AUC คือพื้นที่ของบริเวณสีเทาในภาพประกอบก่อนหน้า ในกรณีพิเศษนี้ พื้นที่คือความยาวของบริเวณสีเทา (1.0) คูณด้วยความกว้างของบริเวณสีเทา (1.0) ดังนั้นผลคูณของ 1.0 และ 1.0 จะให้ AUC เท่ากับ 1.0 ซึ่งเป็นคะแนน AUC สูงสุดที่เป็นไปได้

ในทางกลับกัน เส้นโค้ง ROC ของตัวแยกประเภทที่แยกคลาสไม่ได้เลยจะเป็นดังนี้ พื้นที่ของบริเวณสีเทานี้คือ 0.5

เส้นโค้ง ROC ทั่วไปจะมีลักษณะดังต่อไปนี้

การคํานวณพื้นที่ใต้เส้นโค้งนี้ด้วยตนเองเป็นเรื่องที่ยุ่งยากมาก โปรแกรมจึงมักคํานวณค่า AUC ส่วนใหญ่

---

คลิกไอคอนเพื่อดูคําจํากัดความอย่างเป็นทางการของ AUC

AUC คือความน่าจะเป็นที่ตัวแยกประเภทจะมั่นใจมากขึ้นว่าตัวอย่างเชิงบวกที่เลือกแบบสุ่มเป็นเชิงบวกจริงมากกว่าตัวอย่างเชิงลบที่เลือกแบบสุ่มเป็นเชิงบวก

---

ดูข้อมูลเพิ่มเติมได้ที่การจัดประเภท: ROC และ AUC ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง

ความแม่นยำเฉลี่ยที่ k

#language

#Metric

เมตริกสำหรับสรุปประสิทธิภาพของโมเดลในพรอมต์เดียวซึ่งจะสร้างผลลัพธ์ที่จัดอันดับ เช่น รายการคำแนะนำหนังสือที่มีหมายเลข ความแม่นยำเฉลี่ยที่ k คือค่าเฉลี่ยของค่าความแม่นยำที่ k สำหรับผลการค้นหาที่เกี่ยวข้องแต่ละรายการ ดังนั้น สูตรความแม่นยำเฉลี่ยที่ k จึงจะเป็นดังนี้

\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]

where:

• \(n\) คือจํานวนรายการที่เกี่ยวข้องในรายการ

เปรียบเทียบกับ recall at k

หมายเหตุ: ความแม่นยำเฉลี่ยที่ k จะประเมินเอาต์พุตสำหรับพรอมต์รายการเดียว ใช้ความแม่นยำเฉลี่ยแบบถ่วงน้ำหนักที่ k เพื่อประเมินคุณภาพของเอาต์พุตของโมเดลในพรอมต์ต่างๆ

หมายเหตุ: บางคนเรียกความแม่นยำเฉลี่ยที่ k สั้นๆ ว่าความแม่นยำเฉลี่ย

คลิกไอคอนเพื่อดูตัวอย่าง

สมมติว่าโมเดลภาษาขนาดใหญ่ได้รับคําค้นหาต่อไปนี้

List the 6 funniest movies of all time in order.

และโมเดลภาษาขนาดใหญ่จะแสดงรายการต่อไปนี้

1. The General
2. Mean Girls
3. Platoon
4. Bridesmaids
5. Citizen Kane
6. This is Spinal Tap

ภาพยนตร์ 4 เรื่องในรายการที่แสดงผลตลกมาก (นั่นคือมีความเกี่ยวข้อง) แต่อีก 2 เรื่องเป็นภาพยนตร์แนวดราม่า (ไม่เกี่ยวข้อง) ตารางต่อไปนี้แสดงรายละเอียดผลลัพธ์

ตำแหน่ง	ภาพยนตร์	เกี่ยวข้องไหม	ความแม่นยำที่ k
1	The General	ใช่	1.0
2	Mean Girls	ใช่	1.0
3	Platoon	ไม่	ไม่เกี่ยวข้อง
4	Bridesmaids	ใช่	0.75
5	Citizen Kane	ไม่	ไม่เกี่ยวข้อง
6	This is Spinal Tap	ใช่	0.67

จํานวนผลการค้นหาที่เกี่ยวข้องคือ 4 คุณจึงคํานวณความแม่นยําเฉลี่ยที่ 6 ได้ดังนี้

$${\text{average precision at 6}} = \frac{1}{4} {\text{(1.0 + 1.0 + 0.75 + 0.67)} } $$ $${\text{average precision at 6}} = {\text{~0.85} } $$

---

B

พื้นฐาน

#Metric

โมเดลที่ใช้เป็นจุดอ้างอิงเพื่อเปรียบเทียบประสิทธิภาพของโมเดลอื่น (โดยทั่วไปคือโมเดลที่ซับซ้อนกว่า) เช่น โมเดลการถดถอยเชิงโลจิสติกอาจใช้เป็นบรรทัดฐานที่ดีสําหรับโมเดลเชิงลึก

สําหรับปัญหาหนึ่งๆ เกณฑ์พื้นฐานจะช่วยให้นักพัฒนาโมเดลระบุประสิทธิภาพขั้นต่ำที่คาดหวังซึ่งโมเดลใหม่ต้องบรรลุเพื่อให้โมเดลใหม่มีประโยชน์

C

ต้นทุน

#Metric

คำพ้องความหมายของ loss

ความเป็นธรรมแบบเทียบกับกลุ่มควบคุม

#fairness

#Metric

เมตริกความเป็นธรรมที่ตรวจสอบว่าตัวจัดประเภทให้ผลลัพธ์เหมือนกันสำหรับบุคคลหนึ่งกับอีกคนหนึ่งที่เหมือนกันทุกประการ ยกเว้นแอตทริบิวต์ที่มีความละเอียดอ่อนอย่างน้อย 1 รายการหรือไม่ การประเมินตัวแยกประเภทเพื่อหาความยุติธรรมแบบเทียบเท่าสมมติฐานเป็นวิธีหนึ่งในการค้นหาแหล่งที่มาที่อาจทำให้เกิดอคติในโมเดล

โปรดดูข้อมูลเพิ่มเติมที่หัวข้อต่อไปนี้

• ความเป็นธรรม: ความเป็นธรรมแบบเทียบกับกลุ่มควบคุมในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง
• When Worlds Collide: Integrating Different Counterfactual Assumptions in Fairness

เอนโทรปีครอส

#Metric

การทั่วไปของ Log Loss ไปใช้กับปัญหาการจัดประเภทหลายคลาส การเข้ารหัสไขว้จะวัดความแตกต่างระหว่างการแจกแจงความน่าจะเป็น 2 รายการ โปรดดูความสับสนด้วย

ฟังก์ชันการแจกแจงสะสม (CDF)

#Metric

ฟังก์ชันที่กําหนดความถี่ของตัวอย่างที่น้อยกว่าหรือเท่ากับค่าเป้าหมาย ตัวอย่างเช่น ลองพิจารณาการแจกแจงปกติของค่าต่อเนื่อง CDF บอกคุณว่าตัวอย่างประมาณ 50% ควรน้อยกว่าหรือเท่ากับค่ามัธยฐาน และตัวอย่างประมาณ 84% ควรน้อยกว่าหรือเท่ากับค่าเบี่ยงเบนมาตรฐาน 1 เท่าเหนือค่ามัธยฐาน

D

ความเท่าเทียมด้านข้อมูลประชากร

#fairness

#Metric

เมตริกความเป็นธรรมที่เป็นไปตามข้อกำหนดหากผลการจัดประเภทของโมเดลไม่ขึ้นอยู่กับแอตทริบิวต์ที่ละเอียดอ่อนที่ระบุ

ตัวอย่างเช่น หากทั้งชาวลิลลี่ปุตและชาวบราบิงแน็กสมัครเข้ามหาวิทยาลัยกลุบบัดบรีบ ความเป็นธรรมด้านข้อมูลประชากรจะเกิดขึ้นเมื่อเปอร์เซ็นต์ของชาวลิลลี่ปุตที่ได้รับอนุญาตให้เข้าศึกษาเท่ากับเปอร์เซ็นต์ของชาวบราบิงแน็กที่ได้รับอนุญาตให้เข้าศึกษา โดยไม่คำนึงว่ากลุ่มหนึ่งมีคุณวุฒิมากกว่าอีกกลุ่มโดยเฉลี่ยหรือไม่

ซึ่งต่างจากโอกาสที่เท่าเทียมและความเสมอภาคของโอกาสที่อนุญาตให้ผลการจัดประเภทโดยรวมขึ้นอยู่กับแอตทริบิวต์ที่ละเอียดอ่อน แต่ไม่อนุญาตให้ผลการจัดประเภทสำหรับป้ายกำกับข้อมูลจริงที่ระบุบางรายการขึ้นอยู่กับแอตทริบิวต์ที่ละเอียดอ่อน ดูภาพแสดงการประนีประนอมเมื่อเพิ่มประสิทธิภาพเพื่อลดความเหลื่อมล้ำทางข้อมูลประชากรได้ที่"การต่อสู้กับการแบ่งแยกด้วยแมชชีนเลิร์นนิงที่ฉลาดขึ้น"

ดูข้อมูลเพิ่มเติมได้ที่ความเป็นธรรม: ความเท่าเทียมทางประชากรในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง

E

ระยะทางของรถขุด (EMD)

#Metric

การวัดความคล้ายคลึงสัมพัทธ์ของการแจกแจง 2 รายการ ยิ่งระยะทางของเครื่องจักรขุดดินต่ำ รูปแบบการกระจายก็จะยิ่งคล้ายกัน

แก้ไขระยะทาง

#language

#Metric

การวัดความคล้ายคลึงของสตริงข้อความ 2 รายการ ระยะการแก้ไขมีประโยชน์ในแมชชีนเลิร์นนิงเนื่องจากเหตุผลต่อไปนี้

• ระยะห่างการแก้ไขคํานวณได้ง่าย
• ระยะห่างการแก้ไขจะเปรียบเทียบสตริง 2 รายการที่ทราบว่าคล้ายกัน
• ระยะแก้ไขสามารถระบุระดับที่สตริงต่างๆ คล้ายกับสตริงหนึ่งๆ

ระยะห่างการแก้ไขมีหลายคำจำกัดความ โดยแต่ละคำจำกัดความจะใช้การดำเนินการสตริงที่แตกต่างกัน ดูตัวอย่างได้ที่ระยะ Levenshtein

ฟังก์ชันการแจกแจงสะสมเชิงประจักษ์ (eCDF หรือ EDF)

#Metric

ฟังก์ชันการแจกแจงสะสมซึ่งอิงตามการวัดผลเชิงประจักษ์จากชุดข้อมูลจริง ค่าของฟังก์ชันที่จุดใดก็ได้บนแกน x คือเศษส่วนของค่าสังเกตในชุดข้อมูลที่มีค่าน้อยกว่าหรือเท่ากับค่าที่ระบุ

เอนโทรปี

#df

#Metric

ใน ทฤษฎีสารสนเทศ หมายถึงคำอธิบายความคาดเดาไม่ได้ของรูปแบบความน่าจะเป็น หรืออาจหมายถึงปริมาณข้อมูลที่มีอยู่ในตัวอย่างแต่ละรายการ การแจกแจงข้อมูลจะมีเอนโทรปีสูงสุดเมื่อค่าทั้งหมดของตัวแปรแบบสุ่มมีแนวโน้มเท่าๆ กัน

เอนโทรปีของชุดที่มีค่าที่เป็นไปได้ 2 ค่า ได้แก่ "0" และ "1" (เช่น ป้ายกำกับในปัญหาการจัดประเภทแบบไบนารี) มีสูตรดังนี้

  H = -p log p - q log q = -p log p - (1-p) * log (1-p)

where:

• H คือเอนโทรปี
• p คือเศษส่วนของตัวอย่าง "1"
• q คือเศษส่วนของตัวอย่าง "0" โปรดทราบว่า q = (1 - p)
• log โดยทั่วไปคือ log₂ ในกรณีนี้ หน่วยของข้อมูลเชิงซ้อนคือบิต

ตัวอย่างเช่น สมมติว่า

• ตัวอย่าง 100 รายการมีค่าเป็น "1"
• ตัวอย่าง 300 รายการมีค่าเป็น "0"

ดังนั้น ค่าเอนโทรปีคือ

• p = 0.25
• q = 0.75
• H = (-0.25)log₂(0.25) - (0.75)log₂(0.75) = 0.81 บิตต่อตัวอย่าง

ชุดข้อมูลที่สมดุลกันโดยสมบูรณ์ (เช่น "0" 200 ตัวและ "1" 200 ตัว) จะมีเอนโทรปี 1.0 บิตต่อตัวอย่าง เมื่อชุดข้อมูลมีความไม่สมดุลมากขึ้น เอนโทรปีของชุดข้อมูลจะเข้าใกล้ 0.0

ในต้นไม้การตัดสินใจ เอนโทรปีช่วยสร้างการได้ข้อมูลเพื่อช่วยตัวแยกเลือกเงื่อนไขขณะที่ต้นไม้การตัดสินใจการจัดประเภทเติบโต

เปรียบเทียบเอนโทรปีกับข้อมูลต่อไปนี้

• ความไม่เป็นระเบียบของ gini
• ฟังก์ชันการสูญเสียCross-Entropy

บางครั้งจะเรียกเอนโทรปีว่าเอนโทรปีของ Shannon

ดูข้อมูลเพิ่มเติมได้ในตัวแยกที่ตรงกันทั้งหมดสำหรับการแยกประเภทแบบ 2 กลุ่มด้วยฟีเจอร์ที่เป็นตัวเลขในหลักสูตรป่าการตัดสินใจ

โอกาสที่เท่าเทียมกัน

#fairness

#Metric

เมตริกความเป็นธรรมเพื่อประเมินว่าโมเดลคาดการณ์ผลลัพธ์ที่ต้องการได้ดีเท่าๆ กันสำหรับค่าทั้งหมดของแอตทริบิวต์ที่มีความละเอียดอ่อนหรือไม่ กล่าวคือ หากผลลัพธ์ที่ต้องการสำหรับโมเดลคือคลาสที่เป็นบวก เป้าหมายคืออัตราผลบวกจริงจะเหมือนกันสำหรับทุกกลุ่ม

โอกาสที่เท่าเทียมเกี่ยวข้องกับอัตราต่อรองที่เท่าเทียม ซึ่งกำหนดว่าทั้งอัตราผลบวกจริงและอัตราผลบวกลวงต้องเหมือนกันสำหรับทุกกลุ่ม

สมมติว่ามหาวิทยาลัย Glubbdubdrib รับทั้งชาวลิลลี่ปุตและชาวบราบิงแน็กเรียนหลักสูตรคณิตศาสตร์ที่เข้มงวด โรงเรียนมัธยมของชาวลิลลี่ปุตตินำเสนอหลักสูตรคณิตศาสตร์ที่มีประสิทธิภาพ และนักเรียนส่วนใหญ่มีสิทธิ์เข้าเรียนในมหาวิทยาลัย โรงเรียนมัธยมของชาวบราบิงกันไม่ได้เปิดสอนวิชาคณิตศาสตร์เลย ส่งผลให้นักเรียนมีจำนวนน้อยกว่ามากที่มีคุณสมบัติตรงตามข้อกำหนด โอกาสที่เท่าเทียมกันเป็นไปตามป้ายกำกับที่ต้องการว่า "ได้รับอนุญาต" เกี่ยวกับสัญชาติ (Lilliputian หรือ Brobdingnagian) หากนักเรียนที่มีสิทธิ์มีโอกาสเท่าๆ กันที่จะได้รับการอนุญาต ไม่ว่านักเรียนจะเป็น Lilliputian หรือ Brobdingnagian

ตัวอย่างเช่น สมมติว่าชาวลิลลี่ปุต 100 คนและชาวบราบิงแน็ก 100 คนสมัครเข้ามหาวิทยาลัยกลุบบัดบรีบ และผลการตัดสินการรับสมัครมีดังนี้

ตารางที่ 1 ผู้สมัคร Lilliputian (90% มีสิทธิ์)

	เข้าเกณฑ์	คุณสมบัติไม่ครบ
ยอมรับ	45	3
ถูกปฏิเสธ	45	7
รวม	90	10
เปอร์เซ็นต์ของนักเรียนที่มีสิทธิ์ได้รับค่าเล่าเรียน: 45/90 = 50% เปอร์เซ็นต์ของนักเรียนที่ไม่มีสิทธิ์ได้รับค่าเล่าเรียน: 7/10 = 70% เปอร์เซ็นต์ทั้งหมดของนักเรียน Lilliputian ที่ได้รับค่าเล่าเรียน: (45+3)/100 = 48%

 

ตารางที่ 2 ผู้สมัครที่มีคุณสมบัติตรงตามเกณฑ์ (10%)

	เข้าเกณฑ์	คุณสมบัติไม่ครบ
ยอมรับ	5	9
ถูกปฏิเสธ	5	81
รวม	10	90
เปอร์เซ็นต์ของนักเรียนที่มีสิทธิ์ได้รับอนุญาตให้เข้าเรียน: 5/10 = 50% เปอร์เซ็นต์ของนักเรียนที่ไม่มีสิทธิ์ได้รับอนุญาตให้เข้าเรียน: 81/90 = 90% เปอร์เซ็นต์ทั้งหมดของนักเรียน Brobdingnagian ที่ได้รับอนุญาตให้เข้าเรียน: (5+9)/100 = 14%

ตัวอย่างข้างต้นเป็นไปตามความเท่าเทียมของโอกาสในการรับนักเรียนที่มีสิทธิ์ เนื่องจากทั้งชาวลิลลี่ปุตและชาวบราบิงแนกันที่มีสิทธิ์มีโอกาส 50% ที่จะได้รับการยอมรับ

แม้ว่าจะเป็นไปตามหลักความเท่าเทียมกันของโอกาส แต่เมตริกความเท่าเทียม 2 รายการต่อไปนี้ไม่เป็นไปตามหลักดังกล่าว

• ความเท่าเทียมทางประชากร: นักเรียนชาวลิลลี่ปุตและชาวบราบิงแนกได้รับอนุญาตให้เข้ามหาวิทยาลัยในอัตราที่แตกต่างกัน โดยนักเรียนชาวลิลลี่ปุตได้รับอนุญาตให้เข้ามหาวิทยาลัย 48% แต่นักเรียนชาวบราบิงแนกได้รับอนุญาตให้เข้ามหาวิทยาลัยเพียง 14%
• โอกาสที่เท่าเทียม: แม้ว่านักเรียน Lilliputian และ Brobdingnagian ที่มีสิทธิ์จะมีสิทธิ์ได้รับการยอมรับเท่าๆ กัน แต่ข้อจำกัดเพิ่มเติมที่ว่านักเรียน Lilliputian และ Brobdingnagian ที่ไม่มีสิทธิ์จะมีสิทธิ์ถูกปฏิเสธเท่าๆ กันนั้นไม่ได้รับการยอมรับ ผู้ที่มีคุณสมบัติไม่ตรงตามเกณฑ์ของ Lilliputians มีอัตราการถูกปฏิเสธ 70% ส่วนผู้ที่มีคุณสมบัติไม่ตรงตามเกณฑ์ของ Brobdingnagians มีอัตราการถูกปฏิเสธ 90%

ดูข้อมูลเพิ่มเติมได้ที่ความเป็นธรรม: ความเท่าเทียมของโอกาสในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง

โอกาสที่เท่ากัน

#fairness

#Metric

เมตริกความเท่าเทียมเพื่อประเมินว่าโมเดลคาดการณ์ผลลัพธ์ได้ดีเท่าๆ กันสำหรับค่าทั้งหมดของแอตทริบิวต์ที่มีความละเอียดอ่อนทั้งในแง่ของคลาสบวกและคลาสลบ ไม่ใช่แค่คลาสใดคลาสหนึ่งโดยเฉพาะ กล่าวคือ ทั้งอัตราผลบวกจริงและอัตราผลลบเท็จควรเหมือนกันสำหรับทุกกลุ่ม

อัตราต่อรองที่เท่ากันเกี่ยวข้องกับความเท่าเทียมของโอกาส ซึ่งมุ่งเน้นที่อัตราข้อผิดพลาดของคลาสเดียวเท่านั้น (บวกหรือลบ)

ตัวอย่างเช่น สมมติว่ามหาวิทยาลัย Glubbdubdrib ยอมรับทั้งชาวลิลลี่ปุตและชาวบราบิงแนกเรียนหลักสูตรคณิตศาสตร์ที่เข้มงวด โรงเรียนมัธยมของชาวลิลลี่ปุตติมีหลักสูตรคณิตศาสตร์ที่เข้มข้น และนักเรียนส่วนใหญ่มีสิทธิ์เข้าเรียนในมหาวิทยาลัย โรงเรียนมัธยมของชาวบราบิงกันไม่ได้เปิดสอนวิชาคณิตศาสตร์เลย ส่งผลให้นักเรียนมีจำนวนน้อยกว่ามากที่มีคุณสมบัติตรงตามข้อกำหนด โอกาสที่เท่าเทียมกันจะเป็นไปตามข้อกำหนดไม่ว่าผู้สมัครจะมีสิทธิ์หรือไม่ก็ตาม หากมีสิทธิ์ ก็มีโอกาสเท่าๆ กันที่จะได้รับการยอมรับเข้าโปรแกรม และหากไม่มีสิทธิ์ ก็มีโอกาสเท่าๆ กันที่จะถูกปฏิเสธ

สมมติว่าชาวลิลลี่ปุต 100 คนและชาวบราบิงแน็ก 100 คนสมัครเข้ามหาวิทยาลัยกลุบบัดดริบ และผลการตัดสินการรับสมัครมีดังนี้

ตารางที่ 3 ผู้สมัคร Lilliputian (90% มีสิทธิ์)

	เข้าเกณฑ์	คุณสมบัติไม่ครบ
ยอมรับ	45	2
ถูกปฏิเสธ	45	8
รวม	90	10
เปอร์เซ็นต์ของนักเรียนที่มีสิทธิ์ได้รับอนุญาตให้เข้าเรียน: 45/90 = 50% เปอร์เซ็นต์ของนักเรียนที่ไม่มีสิทธิ์ได้รับอนุญาตให้เข้าเรียน: 8/10 = 80% เปอร์เซ็นต์ทั้งหมดของนักเรียน Lilliputian ได้รับอนุญาตให้เข้าเรียน: (45+2)/100 = 47%

 

ตารางที่ 4 ผู้สมัครที่มีคุณสมบัติตรงตามเกณฑ์ (10%)

	เข้าเกณฑ์	คุณสมบัติไม่ครบ
ยอมรับ	5	18
ถูกปฏิเสธ	5	72
รวม	10	90
เปอร์เซ็นต์ของนักเรียนที่มีสิทธิ์ได้รับอนุญาตให้เข้าเรียน: 5/10 = 50% เปอร์เซ็นต์ของนักเรียนที่ไม่มีสิทธิ์ได้รับอนุญาตให้เข้าเรียน: 72/90 = 80% เปอร์เซ็นต์ทั้งหมดของนักเรียน Brobdingnagian ที่ได้รับอนุญาตให้เข้าเรียน: (5+18)/100 = 23%

เงื่อนไขความน่าจะเป็นที่เท่ากันเป็นไปตามเกณฑ์เนื่องจากทั้งนักเรียน Lilliputian และ Brobdingnagian ที่มีสิทธิ์มีโอกาส 50% ที่จะได้รับการยอมรับ และนักเรียน Lilliputian และ Brobdingnagian ที่ไม่มีสิทธิ์มีโอกาส 80% ที่จะถูกปฏิเสธ

หมายเหตุ: แม้ว่าโอกาสที่เท่าเทียมกันจะเป็นไปตามเกณฑ์ที่นี่ แต่ความเท่าเทียมด้านข้อมูลประชากรไม่เป็นไปตามเกณฑ์ นักศึกษาชาวลิลลี่ปุตินและชาวบราบิงแนกันได้รับอนุญาตให้เข้าเรียนที่มหาวิทยาลัยกลุบบัดบรีบในอัตราที่แตกต่างกัน โดยนักศึกษาชาวลิลลี่ปุตินได้รับอนุญาตให้เข้าเรียน 47% และนักศึกษาชาวบราบิงแนกันได้รับอนุญาตให้เข้าเรียน 23%

โอกาสที่เท่าเทียมกันได้รับการกําหนดอย่างเป็นทางการใน"ความเท่าเทียมของโอกาสในการเรียนรู้แบบควบคุม" ดังนี้ "ตัวทำนาย Ŷ เป็นไปตามความเท่าเทียมของโอกาสในแง่ของแอตทริบิวต์ที่ได้รับการคุ้มครอง A และผลลัพธ์ Y หาก Ŷ และ A เป็นอิสระต่อกันโดยขึ้นกับ Y"

หมายเหตุ: เปรียบเทียบโอกาสที่เท่าเทียมกับเมตริกความเท่าเทียมของโอกาสที่ผ่อนคลายกว่า

evals

#language

#generativeAI

#Metric

ใช้เป็นหลักเป็นตัวย่อของการประเมิน LLM evals ย่อมาจากการประเมินทุกรูปแบบ

การประเมิน

#language

#generativeAI

#Metric

กระบวนการวัดคุณภาพของรูปแบบหรือการเปรียบเทียบรูปแบบต่างๆ

หากต้องการประเมินโมเดลแมชชีนเลิร์นนิงที่มีการควบคุมดูแล โดยทั่วไปคุณจะต้องประเมินโมเดลนั้นเทียบกับชุดการตรวจสอบและชุดทดสอบ การประเมิน LLMมักเกี่ยวข้องกับการประเมินคุณภาพและความปลอดภัยในวงกว้าง

F

F₁

#Metric

เมตริกการจัดประเภทแบบ 2 กลุ่ม "แบบรวม" ที่อาศัยทั้งความแม่นยำและความแม่นยำในการจดจำ สูตรมีดังนี้

$$F{_1} = \frac{\text{2 * precision * recall}} {\text{precision + recall}}$$

คลิกไอคอนเพื่อดูตัวอย่าง

สมมติว่าความแม่นยำและการจดจํามีค่าดังต่อไปนี้

• precision = 0.6
• recall = 0.4

คุณคํานวณ F₁ ดังนี้

$$F{_1} = \frac{\text{2 * 0.6 * 0.4}} {\text{0.6 + 0.4}} = 0.48$$

เมื่อความแม่นยำและความแม่นยำในการจดจำค่อนข้างคล้ายกัน (เช่น ในตัวอย่างก่อนหน้านี้) F₁ จะใกล้เคียงกับค่าเฉลี่ย เมื่อความแม่นยำและการเรียกคืนแตกต่างกันอย่างมาก F₁ จะใกล้เคียงกับค่าที่ต่ำลง เช่น

• precision = 0.9
• recall = 0.1

$$F{_1} = \frac{\text{2 * 0.9 * 0.1}} {\text{0.9 + 0.1}} = 0.18$$

---

เมตริกความยุติธรรม

#fairness

#Metric

คําจํากัดความทางคณิตศาสตร์ของ "ความเป็นธรรม" ที่วัดผลได้ เมตริกความเป็นธรรมที่ใช้กันโดยทั่วไป ได้แก่

• การกระจายความเสี่ยง
• ความเท่าเทียมตามการคาดการณ์
• ความยุติธรรมแบบเทียบกับสิ่งที่ไม่ได้เกิดขึ้น
• ความเท่าเทียมทางประชากร

เมตริกความยุติธรรมหลายรายการใช้ร่วมกันไม่ได้ โปรดดูความเข้ากันไม่ได้ของเมตริกความยุติธรรม

ผลลบลวง (FN)

#fundamentals

#Metric

ตัวอย่างที่โมเดลคาดการณ์คลาสเชิงลบอย่างไม่ถูกต้อง เช่น โมเดลคาดการณ์ว่าข้อความอีเมลหนึ่งๆ ไม่ใช่สแปม (คลาสเชิงลบ) แต่ข้อความอีเมลนั้นเป็นจดหมายขยะจริงๆ

อัตราผลลบลวง

#Metric

สัดส่วนของตัวอย่างเชิงบวกจริงที่โมเดลคาดการณ์คลาสเชิงลบอย่างไม่ถูกต้อง สูตรต่อไปนี้จะคํานวณอัตราเชิงลบที่ไม่ถูกต้อง

$$\text{false negative rate} = \frac{\text{false negatives}}{\text{false negatives} + \text{true positives}}$$

ดูข้อมูลเพิ่มเติมเกี่ยวกับเกณฑ์และตารางความสับสนในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง

ผลบวกลวง (FP)

#fundamentals

#Metric

ตัวอย่างที่โมเดลคาดการณ์คลาสบวกอย่างไม่ถูกต้อง เช่น โมเดลคาดการณ์ว่าข้อความอีเมลหนึ่งๆ เป็นจดหมายขยะ (คลาสเชิงบวก) แต่ข้อความอีเมลนั้นไม่ใช่จดหมายขยะจริงๆ

ดูข้อมูลเพิ่มเติมเกี่ยวกับเกณฑ์และตารางความสับสนในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง

อัตราผลบวกลวง (FPR)

#fundamentals

#Metric

สัดส่วนของตัวอย่างเชิงลบจริงที่โมเดลคาดการณ์คลาสที่เป็นบวกอย่างไม่ถูกต้อง สูตรต่อไปนี้จะคํานวณอัตราผลบวกลวง

$$\text{false positive rate} = \frac{\text{false positives}}{\text{false positives} + \text{true negatives}}$$

อัตราผลบวกลวงคือแกน x ในกราฟ ROC

ดูข้อมูลเพิ่มเติมได้ที่การจัดประเภท: ROC และ AUC ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง

ความสำคัญของฟีเจอร์

#df

#Metric

คำพ้องความหมายของความสำคัญของตัวแปร

เศษส่วนของความสําเร็จ

#generativeAI

#Metric

เมตริกสําหรับประเมินข้อความที่สร้างขึ้นของโมเดล ML ส่วนที่เป็นความสำเร็จคือจํานวนเอาต์พุตข้อความที่ "สําเร็จ" หารด้วยจํานวนเอาต์พุตข้อความทั้งหมดที่สร้างขึ้น ตัวอย่างเช่น หากโมเดลภาษาขนาดใหญ่สร้างโค้ด 10 บล็อก โดย 5 บล็อกทำงานสำเร็จ เศษส่วนของความสําเร็จจะเท่ากับ 50%

แม้ว่าเศษส่วนของความสําเร็จจะมีประโยชน์อย่างกว้างๆ ในสถิติ แต่ภายใน ML เมตริกนี้มีประโยชน์สําหรับการวัดงานที่ตรวจสอบได้เป็นหลัก เช่น การสร้างโค้ดหรือโจทย์คณิตศาสตร์

G

ความไม่บริสุทธิ์ของจีนี

#df

#Metric

เมตริกที่คล้ายกับเอนโทรปี ตัวแยกใช้ค่าที่มาจากความไม่บริสุทธิ์ของ Gini หรือเอนโทรปีเพื่อสร้างเงื่อนไขสําหรับการจัดประเภทต้นไม้การตัดสินใจ การได้ข้อมูลมาจากเอนโทรปี ไม่มีคําที่เทียบเท่าซึ่งยอมรับกันทั่วโลกสําหรับเมตริกที่มาจากความไม่บริสุทธิ์ของ Gini แต่เมตริกที่ไม่มีชื่อนี้สําคัญพอๆ กับข้อมูลที่ได้รับ

ความไม่เป็นระเบียบของจีนีเรียกอีกอย่างว่าดัชนีจีนี หรือเรียกสั้นๆ ว่าจีนี

คลิกไอคอนเพื่อดูรายละเอียดทางคณิตศาสตร์เกี่ยวกับความไม่บริสุทธิ์ของ Gini

ความไม่เป็นระเบียบของ Gini คือความน่าจะเป็นที่จะจัดประเภทข้อมูลใหม่ไม่ถูกต้องซึ่งนำมาจากการแจกแจงเดียวกัน ความไม่เป็นระเบียบของ Gini ของชุดที่มีค่าที่เป็นไปได้ 2 ค่า ได้แก่ "0" และ "1" (เช่น ป้ายกำกับในปัญหาการจัดประเภทแบบ 2 กลุ่ม) จะคํานวณจากสูตรต่อไปนี้

   I = 1 - (p² + q²) = 1 - (p² + (1-p)²)

where:

• I คือความไม่บริสุทธิ์ของ Gini
• p คือเศษส่วนของตัวอย่าง "1"
• q คือเศษส่วนของตัวอย่าง "0" โปรดทราบว่า q = 1-p

ตัวอย่างเช่น ลองพิจารณาชุดข้อมูลต่อไปนี้

• ป้ายกำกับ 100 รายการ (0.25 ของชุดข้อมูล) มีค่าเป็น "1"
• ป้ายกำกับ 300 รายการ (0.75 ของชุดข้อมูล) มีค่าเป็น "0"

ดังนั้น ความบริสุทธิ์ของ Gini คือ

• p = 0.25
• q = 0.75
• I = 1 - (0.25² + 0.75²) = 0.375

ดังนั้น ป้ายกำกับแบบสุ่มจากชุดข้อมูลเดียวกันจึงมีโอกาส 37.5% ที่จะจัดประเภทไม่ถูกต้อง และมีโอกาส 62.5% ที่จะจัดประเภทอย่างถูกต้อง

ป้ายกำกับที่สมดุลอย่างสมบูรณ์ (เช่น "0" 200 ตัวและ "1" 200 ตัว) จะมีค่าความไม่บริสุทธิ์ของจินี 0.5 ป้ายกำกับที่ไม่สมดุลอย่างมากจะมีค่าความไม่บริสุทธิ์ของจินีใกล้เคียงกับ 0.0

---

H

บานพับขาด

#Metric

ตระกูลฟังก์ชันการสูญเสียสําหรับการจัดประเภทที่ออกแบบมาเพื่อค้นหาขอบเขตการตัดสินให้อยู่ห่างจากตัวอย่างการฝึกแต่ละรายการมากที่สุด ด้วยเหตุนี้จึงเพิ่มระยะห่างระหว่างตัวอย่างกับขอบเขตให้มากที่สุด KSVM ใช้การสูญเสียแบบ hinge (หรือฟังก์ชันที่เกี่ยวข้อง เช่น การสูญเสียแบบ hinge ยกกำลัง 2) สําหรับการจัดประเภทแบบไบนารี ฟังก์ชันการสูญเสียแบบ hinge จะกําหนดดังนี้

$$\text{loss} = \text{max}(0, 1 - (y * y'))$$

โดยที่ y คือป้ายกำกับจริง ซึ่งอาจเป็น -1 หรือ +1 และ y' คือเอาต์พุตดิบของโมเดลการจัดประเภท

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

ดังนั้น ผังความสูญเสียของ hinge เทียบกับ (y * y') จะมีลักษณะดังนี้

I

ความไม่เข้ากันได้ของเมตริกความยุติธรรม

#fairness

#Metric

แนวคิดที่ว่าแนวคิดบางอย่างเกี่ยวกับความยุติธรรมนั้นใช้ร่วมกันไม่ได้และไม่สามารถบรรลุพร้อมกัน ด้วยเหตุนี้ จึงไม่มีเมตริกที่เป็นสากลเพียงเมตริกเดียวสำหรับวัดความเป็นธรรมซึ่งใช้ได้กับปัญหา ML ทั้งหมด

แม้ว่าเรื่องนี้อาจฟังดูท้อแท้ แต่การที่เมตริกความยุติธรรมใช้ร่วมกันไม่ได้ไม่ได้หมายความว่าความพยายามด้านความยุติธรรมจะไร้ผล แต่แนะนําว่าต้องกําหนดความยุติธรรมตามบริบทสําหรับปัญหา ML หนึ่งๆ โดยมีเป้าหมายเพื่อป้องกันอันตรายที่เฉพาะเจาะจงสําหรับ Use Case นั้นๆ

ดูการพูดคุยเรื่องความเข้ากันไม่ได้ของเมตริกความเป็นธรรมอย่างละเอียดได้ที่"On the (im)possibility of fairness"

ความยุติธรรมต่อบุคคล

#fairness

#Metric

เมตริกความยุติธรรมที่ตรวจสอบว่าระบบจัดประเภทบุคคลที่คล้ายกันคล้ายกันหรือไม่ ตัวอย่างเช่น Brobdingnagian Academy อาจต้องการสร้างความเป็นธรรมให้กับบุคคล โดยตรวจสอบว่านักเรียน 2 คนที่มีคะแนนเหมือนกันและคะแนนสอบมาตรฐานมีแนวโน้มที่จะได้รับการยอมรับเท่าๆ กัน

โปรดทราบว่าความยุติธรรมของแต่ละบุคคลขึ้นอยู่กับวิธีที่คุณกำหนด "ความคล้ายคลึง" ทั้งหมด (ในกรณีนี้คือคะแนนและคะแนนสอบ) และคุณอาจเสี่ยงที่จะทำให้เกิดปัญหาความยุติธรรมใหม่ๆ หากเมตริกความคล้ายคลึงของคุณขาดข้อมูลสำคัญ (เช่น ความยากของหลักสูตรของนักเรียน)

ดูการพูดคุยเรื่องความยุติธรรมของแต่ละบุคคลอย่างละเอียดได้ที่"ความยุติธรรมผ่านความรู้"

ข้อมูลที่ได้รับ

#df

#Metric

ในป่าการตัดสินใจ ความแตกต่างระหว่างเอนโทรปีของโหนดกับผลรวมของเอนโทรปีของโหนดย่อยที่มีน้ำหนัก (ตามจำนวนตัวอย่าง) เอนโทรปีของโหนดคือเอนโทรปีของตัวอย่างในโหนดนั้น

ตัวอย่างเช่น ลองพิจารณาค่าเอนโทรปีต่อไปนี้

• เอนโทรปีของโหนดหลัก = 0.6
• เอนโทรปีของโหนดย่อย 1 รายการที่มีตัวอย่างที่เกี่ยวข้อง 16 รายการ = 0.2
• เอนโทรปีของโหนดย่อยอีกโหนดหนึ่งซึ่งมีตัวอย่างที่เกี่ยวข้อง 24 รายการ = 0.1

ดังนั้น 40% ของตัวอย่างจะอยู่ในโหนดย่อยโหนดหนึ่ง และ 60% จะอยู่ในโหนดย่อยอีกโหนดหนึ่ง ดังนั้น

• ผลรวมของเอนโทรปีถ่วงน้ำหนักของโหนดย่อย = (0.4 * 0.2) + (0.6 * 0.1) = 0.14

ดังนั้น ข้อมูลที่ได้รับคือ

• อัตราข้อมูลที่ได้รับ = เอนโทรปีของโหนดหลัก - ผลรวมของเอนโทรปีที่ถ่วงน้ำหนักของโหนดย่อย
• ข้อมูลที่ได้รับ = 0.6 - 0.14 = 0.46

ตัวแยกส่วนใหญ่พยายามสร้างเงื่อนไขเพื่อเพิ่มปริมาณข้อมูลที่ได้สูงสุด

ความสอดคล้องกันระหว่างผู้ประเมิน

#Metric

การวัดความถี่ที่ผู้ประเมินที่เป็นมนุษย์เห็นด้วยเมื่อทำภารกิจ หากผู้ประเมินไม่เห็นด้วย คุณอาจต้องปรับปรุงวิธีการของงาน บางครั้งอาจเรียกว่าความสอดคล้องกันของผู้กำกับดูแลหรือความน่าเชื่อถือของผู้ประเมิน ดูข้อมูลเพิ่มเติมได้ที่ค่า Kappa ของ Cohen ซึ่งเป็นวิธีการวัดความสอดคล้องกันระหว่างผู้ประเมินที่ได้รับความนิยมมากที่สุดวิธีหนึ่ง

ดูข้อมูลเพิ่มเติมได้ที่ข้อมูลเชิงหมวดหมู่: ปัญหาที่พบได้ทั่วไปในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง

L

แพ้ L₁

#fundamentals

#Metric

ฟังก์ชันการสูญเสียที่คำนวณค่าสัมบูรณ์ของความแตกต่างระหว่างค่าป้ายกำกับจริงกับค่าที่โมเดลคาดการณ์ ตัวอย่างเช่น ต่อไปนี้คือการคํานวณการสูญเสีย L₁ สําหรับกลุ่มตัวอย่าง 5 รายการ

ค่าจริงของตัวอย่าง	ค่าที่คาดการณ์ของโมเดล	ค่าสัมบูรณ์ของเดลต้า
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = แพ้ L1

ผลต่าง L₁ ไวต่อค่าผิดปกติน้อยกว่าผลต่าง L₂

ค่าเฉลี่ยความผิดพลาดสัมบูรณ์คือค่าเฉลี่ยของการสูญเสีย L₁ ต่อตัวอย่าง

คลิกไอคอนเพื่อดูคณิตศาสตร์แบบเป็นทางการ

$$ L_1 loss = \sum_{i=0}^n | y_i - \hat{y}_i |$$

where:

• $n$ คือจํานวนตัวอย่าง
• $y$ คือค่าจริงของป้ายกํากับ
• $\hat{y}$ คือค่าที่โมเดลคาดการณ์สำหรับ $y$

---

ดูข้อมูลเพิ่มเติมได้ในหัวข้อการหาค่าสัมประสิทธ์เชิงเส้น: ค่าการสูญเสียในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง

อัตราสูญเสีย L₂

#fundamentals

#Metric

ฟังก์ชันการสูญเสียที่คำนวณผลคูณของความแตกต่างระหว่างค่าป้ายกำกับจริงกับค่าที่โมเดลคาดการณ์ ตัวอย่างเช่น นี่คือการคำนวณความสูญเสีย L₂ สําหรับกลุ่มตัวอย่าง 5 รายการ

ค่าจริงของตัวอย่าง	ค่าที่คาดการณ์ของโมเดล	ตารางของเดลต้า
7	6	1
5	4	1
8	11	9
4	6	4
9	8	1
		16 = แพ้ L2

เนื่องจากการยกกำลัง 2 จะทำให้ความสูญเสีย L₂ ขยายอิทธิพลของค่าผิดปกติ กล่าวคือ ผลลัพธ์ L₂ จะตอบสนองต่อการคาดการณ์ที่ไม่ดีมากกว่าผลลัพธ์ L₁ เช่น อัตราสูญเสีย L₁ ของกลุ่มก่อนหน้าจะเป็น 8 ไม่ใช่ 16 โปรดทราบว่าค่าที่ผิดปกติรายการเดียวคิดเป็น 9 จาก 16

โมเดลการหาค่าสัมพัทธ์มักใช้การสูญเสีย L₂ เป็นฟังก์ชันการสูญเสีย

ความคลาดเคลื่อนกำลังสองเฉลี่ยคือค่าเฉลี่ยของการสูญเสีย L₂ ต่อตัวอย่าง ความสูญเสียแบบยกกำลังสองเป็นชื่อเรียกอีกอย่างของความสูญเสีย L₂

คลิกไอคอนเพื่อดูคณิตศาสตร์แบบเป็นทางการ

$$ L_2 loss = \sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$

where:

• $n$ คือจํานวนตัวอย่าง
• $y$ คือค่าจริงของป้ายกํากับ
• $\hat{y}$ คือค่าที่โมเดลคาดการณ์สำหรับ $y$

---

ดูข้อมูลเพิ่มเติมได้ที่การถดถอยเชิงเส้นโลจิสติก: การสูญเสียและการควบคุมในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง

การประเมิน LLM (evals)

#language

#generativeAI

#Metric

ชุดเมตริกและการเปรียบเทียบเพื่อประเมินประสิทธิภาพของโมเดลภาษาขนาดใหญ่ (LLM) การประเมิน LLM ในระดับสูงมีดังนี้

• ช่วยให้นักวิจัยระบุด้านที่ LLM จำเป็นต้องปรับปรุง
• มีประโยชน์ในการเปรียบเทียบ LLM ต่างๆ และระบุ LLM ที่ดีที่สุดสําหรับงานหนึ่งๆ
• ช่วยให้มั่นใจว่า LLM นั้นปลอดภัยและใช้งานได้อย่างมีจริยธรรม

ดูข้อมูลเพิ่มเติมได้ที่โมเดลภาษาขนาดใหญ่ (LLM) ในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง

แพ้

#fundamentals

#Metric

ในระหว่างการฝึกโมเดลที่มีการควบคุมดูแล เป็นการวัดระยะห่างระหว่างการคาดการณ์ของโมเดลกับป้ายกำกับ

ฟังก์ชันการสูญเสียจะคํานวณการสูญเสีย

ดูข้อมูลเพิ่มเติมได้ที่การหาค่าสัมประสิทธ์เชิงเส้น: ค่าการสูญเสียในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง

ฟังก์ชันการสูญเสีย

#fundamentals

#Metric

ในระหว่างการฝึกหรือทดสอบ ฟังก์ชันทางคณิตศาสตร์ที่คำนวณการสูญเสียในกลุ่มตัวอย่าง ฟังก์ชันการสูญเสียจะแสดงผลลัพธ์การสูญเสียที่ต่ำลงสำหรับโมเดลที่ทําการคาดการณ์ได้ดี เมื่อเทียบกับโมเดลที่ทําการคาดการณ์ได้ไม่ดี

โดยทั่วไป เป้าหมายของการฝึกคือลดการสูญเสียที่ฟังก์ชันการสูญเสียแสดง

ฟังก์ชันการสูญเสียมีหลายประเภท เลือกฟังก์ชันการสูญเสียที่เหมาะสมสำหรับประเภทโมเดลที่คุณกําลังสร้าง เช่น

• การสูญเสีย L₂ (หรือข้อผิดพลาดกำลังสองเฉลี่ย) คือฟังก์ชันการสูญเสียสําหรับการประมาณเชิงเส้น
• Log Loss คือฟังก์ชันการสูญเสียสําหรับการถดถอยเชิงเส้นโลจิสติก

M

ค่าเฉลี่ยความคลาดเคลื่อนสัมบูรณ์ (MAE)

#Metric

การสูญเสียโดยเฉลี่ยต่อตัวอย่างเมื่อใช้การสูญเสีย L₁ คํานวณค่าเฉลี่ยความผิดพลาดสัมบูรณ์ดังนี้

1. คำนวณการสูญเสีย L₁ ของกลุ่ม
2. หารความสูญเสีย L₁ ด้วยจํานวนตัวอย่างในชุด

คลิกไอคอนเพื่อดูคณิตศาสตร์แบบเป็นทางการ

$$\text{Mean Absolute Error} = \frac{1}{n}\sum_{i=0}^n | y_i - \hat{y}_i |$$

where:

• $n$ คือจํานวนตัวอย่าง
• $y$ คือค่าจริงของป้ายกํากับ
• $\hat{y}$ คือค่าที่โมเดลคาดการณ์สำหรับ $y$

---

ตัวอย่างเช่น ลองพิจารณาการคำนวณการสูญเสีย L₁ ในตัวอย่าง 5 รายการต่อไปนี้

ค่าจริงของตัวอย่าง	ค่าที่คาดการณ์ของโมเดล	การสูญเสีย (ความแตกต่างระหว่างค่าจริงกับค่าที่คาดการณ์)
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		8 = แพ้ L1

ดังนั้น ผลลัพธ์ของ L₁ คือ 8 และจำนวนตัวอย่างคือ 5 ดังนั้น ค่าเฉลี่ยความผิดพลาดสัมบูรณ์คือ

Mean Absolute Error = L1 loss / Number of Examples
Mean Absolute Error = 8/5 = 1.6

เปรียบเทียบค่าเฉลี่ยความคลาดเคลื่อนสัมบูรณ์กับความคลาดเคลื่อนเฉลี่ยกำลังสอง และค่าเฉลี่ยความคลาดเคลื่อนกำลังสองของราก

ความแม่นยำเฉลี่ยของค่าเฉลี่ยที่ k (mAP@k)

#language

#generativeAI

#Metric

ค่าเฉลี่ยทางสถิติของคะแนนความแม่นยำเฉลี่ยที่ k ทั้งหมดในชุดข้อมูลที่ใช้ตรวจสอบ การใช้ความแม่นยำเฉลี่ยที่ k อย่างหนึ่งคือเพื่อตัดสินคุณภาพของคําแนะนําที่ระบบคําแนะนําสร้างขึ้น

แม้ว่าวลี "ค่าเฉลี่ยถ่วงน้ำหนัก" จะฟังดูซ้ำซ้อน แต่ชื่อเมตริกก็เหมาะสม ท้ายที่สุดแล้ว เมตริกนี้จะหาค่ามัธยฐานของความแม่นยําเฉลี่ยที่ k หลายค่า

คลิกไอคอนเพื่อดูตัวอย่าง

สมมติว่าคุณสร้างระบบการแนะนำที่สร้างรายการนวนิยายแนะนำที่ปรับเปลี่ยนในแบบของคุณสำหรับผู้ใช้แต่ละราย คุณคำนวณความแม่นยำเฉลี่ย 5 รายการต่อไปนี้ที่คะแนน k (1 คะแนนต่อผู้ใช้ 1 คน) โดยอิงตามความคิดเห็นจากผู้ใช้ที่เลือก

• 0.73
• 0.77
• 0.67
• 0.82
• 0.76

ดังนั้นความแม่นยำเฉลี่ยของค่าเฉลี่ยที่ K จะเท่ากับ

$$\text{mean } = \frac{\text{0.73 + 0.77 + 0.67 + 0.82 + 0.76}} {\text{5}} = \text{0.75}$$

---

ความคลาดเคลื่อนเฉลี่ยกำลังสอง (MSE)

#Metric

การสูญเสียโดยเฉลี่ยต่อตัวอย่างเมื่อใช้การสูญเสีย L₂ คำนวณความคลาดเคลื่อนกำลังสองเฉลี่ยดังนี้

1. คํานวณการสูญเสีย L₂ สําหรับกลุ่ม
2. หารความสูญเสีย L₂ ด้วยจํานวนตัวอย่างในชุด

คลิกไอคอนเพื่อดูคณิตศาสตร์แบบเป็นทางการ

$$\text{Mean Squared Error} = \frac{1}{n}\sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$ where:

• $n$ คือจํานวนตัวอย่าง
• $y$ คือค่าจริงของป้ายกํากับ
• $\hat{y}$ คือค่าคาดการณ์ของโมเดลสําหรับ $y$

---

ตัวอย่างเช่น ลองพิจารณาการสูญเสียในตัวอย่าง 5 รายการต่อไปนี้

มูลค่าที่แท้จริง	การคาดการณ์ของโมเดล	แพ้	ผลต่างของค่ากำลังสอง
7	6	1	1
5	4	1	1
8	11	3	9
4	6	2	4
9	8	1	1
			16 = แพ้ L2

ดังนั้น ความคลาดเคลื่อนเฉลี่ยกำลังสองคือ

Mean Squared Error = L2 loss / Number of Examples
Mean Squared Error = 16/5 = 3.2

ความคลาดเคลื่อนเฉลี่ยกำลังสองเป็นเครื่องมือเพิ่มประสิทธิภาพการฝึกอบรมที่ได้รับความนิยม โดยเฉพาะสําหรับการถดถอยเชิงเส้น

เปรียบเทียบความคลาดเคลื่อนกำลังสองเฉลี่ยกับค่าเฉลี่ยความคลาดเคลื่อนสัมบูรณ์ และค่าเฉลี่ยความคลาดเคลื่อนกำลังสองของราก

TensorFlow Playground ใช้ Mean Squared Error เพื่อคํานวณค่าการสูญเสีย

คลิกไอคอนเพื่อดูรายละเอียดเพิ่มเติมเกี่ยวกับค่าที่ผิดปกติ

ค่าผิดปกติส่งผลต่อความคลาดเคลื่อนกำลังสองเฉลี่ยอย่างมาก เช่น ผลขาดทุน 1 คือผลขาดทุนยกกำลัง 2 เท่ากับ 1 แต่ผลขาดทุน 3 คือผลขาดทุนยกกำลัง 2 เท่ากับ 9 ในตารางก่อนหน้านี้ ตัวอย่างที่มีผลลัพธ์เป็นลบ 3 รายการคิดเป็นสัดส่วนประมาณ 56% ของข้อผิดพลาดผลรวมของสี่เหลี่ยมจัตุรัส ขณะที่ตัวอย่างแต่ละรายการที่มีผลลัพธ์เป็นลบ 1 รายการคิดเป็นสัดส่วนเพียง 6% ของข้อผิดพลาดผลรวมของสี่เหลี่ยมจัตุรัส

ค่าที่ผิดปกติจะไม่ส่งผลต่อค่าเฉลี่ยความผิดพลาดสัมบูรณ์มากเท่ากับความคลาดเคลื่อนกำลังสองเฉลี่ย ตัวอย่างเช่น บัญชีที่สูญหาย 3 บัญชีคิดเป็นเพียงประมาณ 38% ของค่าเฉลี่ยความผิดพลาดสัมบูรณ์

การตัดเป็นวิธีหนึ่งในการป้องกันไม่ให้ค่าที่ผิดปกติอย่างมากส่งผลเสียต่อความสามารถในการคาดการณ์ของโมเดล

---

เมตริก

#TensorFlow

#Metric

สถิติที่คุณสนใจ

วัตถุประสงค์คือเมตริกที่ระบบแมชชีนเลิร์นนิงพยายามเพิ่มประสิทธิภาพ

Metrics API (tf.metrics)

#Metric

TensorFlow API สําหรับการประเมินโมเดล เช่น tf.metrics.accuracy จะกําหนดความถี่ที่การคาดการณ์ของโมเดลตรงกับป้ายกํากับ

ความเสียหายแบบ Minimax

#Metric

ฟังก์ชันการสูญเสียสําหรับGenerative Adversarial Network ซึ่งอิงตาม Cross-Entropy ระหว่างการแจกแจงข้อมูลที่สร้างและข้อมูลจริง

มีการสูญเสียแบบ Minimax ในบทความแรกเพื่ออธิบาย Generative Adversarial Network

ดูข้อมูลเพิ่มเติมเกี่ยวกับฟังก์ชันการสูญเสียได้ในหลักสูตร Generative Adversarial Networks

ความจุของโมเดล

#Metric

ความซับซ้อนของปัญหาที่โมเดลสามารถเรียนรู้ ยิ่งโมเดลเรียนรู้ปัญหาที่ซับซ้อนได้มากเท่าใด ความสามารถของโมเดลก็จะยิ่งสูงขึ้นเท่านั้น โดยปกติแล้ว ความสามารถของโมเดลจะเพิ่มขึ้นตามจำนวนพารามิเตอร์ของโมเดล ดูคำจำกัดความอย่างเป็นทางการของความสามารถในการจัดประเภทได้ที่มิติข้อมูล VC

N

คลาสเชิงลบ

#fundamentals

#Metric

ในการจัดประเภทแบบไบนารี คลาสหนึ่งจะเรียกว่าบวก และอีกคลาสหนึ่งจะเรียกว่าลบ คลาสที่เป็นบวกคือสิ่งหรือเหตุการณ์ที่โมเดลกำลังทดสอบ และคลาสที่เป็นลบคือความเป็นไปได้อื่นๆ เช่น

• คลาสเชิงลบในการทดสอบทางการแพทย์อาจเป็น "ไม่ใช่เนื้องอก"
• คลาสเชิงลบในตัวจัดประเภทอีเมลอาจเป็น "ไม่ใช่สแปม"

ตรงข้ามกับคลาสที่เป็นบวก

O

วัตถุประสงค์

#Metric

เมตริกที่อัลกอริทึมพยายามเพิ่มประสิทธิภาพ

ฟังก์ชันวัตถุประสงค์

#Metric

สูตรทางคณิตศาสตร์หรือเมตริกที่โมเดลมีเป้าหมายเพื่อเพิ่มประสิทธิภาพ เช่น ฟังก์ชันวัตถุประสงค์สําหรับการหาค่าสัมประสิทธ์เชิงเส้นมักจะเป็นความสูญเสียค่าเฉลี่ยสี่เหลี่ยม ดังนั้น เมื่อฝึกโมเดลการถดถอยเชิงเส้น การฝึกจะมีเป้าหมายเพื่อลดค่าเฉลี่ยของผลต่างของค่าที่คาดการณ์กับค่าจริงที่ยกกำลัง 2

ในบางกรณี เป้าหมายคือเพิ่มฟังก์ชันวัตถุประสงค์ให้มากที่สุด เช่น หากฟังก์ชันวัตถุประสงค์คือความถูกต้อง เป้าหมายคือเพื่อเพิ่มความแม่นยำสูงสุด

โปรดดูloss ด้วย

P

pass at k (pass@k)

#Metric

เมตริกสำหรับพิจารณาคุณภาพของโค้ด (เช่น Python) ที่โมเดลภาษาขนาดใหญ่สร้างขึ้น กล่าวอย่างเจาะจงคือ ผ่านที่ k บอกความเป็นไปได้ที่บล็อกโค้ดที่สร้างขึ้นอย่างน้อย 1 บล็อกจากบล็อกโค้ดที่สร้างขึ้น k บล็อกจะผ่านการทดสอบ 1 หน่วยทั้งหมด

โมเดลภาษาขนาดใหญ่มักสร้างโค้ดที่ดีสำหรับปัญหาการเขียนโปรแกรมที่ซับซ้อนได้ยาก วิศวกรซอฟต์แวร์ปรับตัวให้เข้ากับปัญหานี้โดยกระตุ้นให้โมเดลภาษาขนาดใหญ่สร้างโซลูชันหลายรายการ (k) สำหรับปัญหาเดียวกัน จากนั้นวิศวกรซอฟต์แวร์จะทดสอบโซลูชันแต่ละรายการกับการทดสอบ 1 หน่วย การคํานวณการผ่านที่ k ขึ้นอยู่กับผลลัพธ์ของการทดสอบหน่วยดังนี้

• หากวิธีแก้ปัญหาเหล่านั้นอย่างน้อย 1 วิธีผ่านการทดสอบยูนิต LLM จะผ่านการทดสอบการสร้างโค้ด
• หากไม่มีโซลูชันใดผ่านการทดสอบยูนิต LLM จะไม่ผ่านภารกิจการสร้างโค้ด

สูตรสําหรับการผ่านที่ k มีดังนี้

\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]

โดยทั่วไป ค่า k ที่สูงขึ้นจะให้คะแนนผ่านที่สูงกว่าที่คะแนน k อย่างไรก็ตาม ค่า k ที่สูงขึ้นต้องใช้ทรัพยากรโมเดลภาษาขนาดใหญ่และการทดสอบหน่วยมากขึ้น

คลิกไอคอนเพื่อดูตัวอย่าง

สมมติว่าวิศวกรซอฟต์แวร์ขอให้โมเดลภาษาขนาดใหญ่สร้างโซลูชัน k=10 รายการสําหรับปัญหาการเขียนโค้ดที่ยาก n=50 รายการ ผลลัพธ์มีดังนี้

• บัตร 30 ใบ
• ไม่ผ่าน 20 ครั้ง

คะแนนผ่านที่ 10 จึงเท่ากับ

$$\text{pass at 10} = \frac{\text{30}} {\text{50}} = 0.6$$

---

การแสดง

#Metric

คําที่มีความหมายหลายอย่างดังนี้

• ความหมายมาตรฐานในวิศวกรรมซอฟต์แวร์ กล่าวคือ ซอฟต์แวร์นี้ทำงานได้เร็ว (หรือมีประสิทธิภาพ) เพียงใด
• ความหมายในแมชชีนเลิร์นนิง ประสิทธิภาพจะตอบคำถามที่ว่าโมเดลนี้ถูกต้องเพียงใด กล่าวคือ การคาดการณ์ของโมเดลนั้นแม่นยำเพียงใด

ความสําคัญของตัวแปรการจัดเรียงสับเปลี่ยน

#df

#Metric

ความสำคัญของตัวแปรประเภทหนึ่งที่ประเมินการเพิ่มขึ้นของข้อผิดพลาดในการคาดการณ์ของโมเดลหลังจากการสับเปลี่ยนค่าของฟีเจอร์ ความสำคัญของตัวแปรการสับเปลี่ยนเป็นเมตริกที่ไม่ขึ้นอยู่กับรูปแบบ

ความงงงวย

#Metric

หนึ่งในตัวชี้วัดว่าโมเดลทํางานได้ดีเพียงใด ตัวอย่างเช่น สมมติว่างานของคุณคืออ่านตัวอักษร 2-3 ตัวแรกของคำที่ผู้ใช้พิมพ์ในแป้นพิมพ์โทรศัพท์ และแสดงรายการคำที่เป็นไปได้ซึ่งเติมเต็มได้ ความสับสน P สําหรับงานนี้คือจํานวนการคาดเดาโดยประมาณที่คุณต้องเสนอเพื่อให้รายการของคุณมีคําที่ผู้ใช้พยายามพิมพ์

ความกำกวมเกี่ยวข้องกับCross-Entropy ดังนี้

$$P= 2^{-\text{cross entropy}}$$

คลาสที่เป็นบวก

#fundamentals

#Metric

ชั้นเรียนที่คุณทดสอบ

เช่น คลาสที่เป็นบวกในโมเดลโรคมะเร็งอาจเป็น "เนื้องอก" คลาสที่เป็นบวกในตัวจัดประเภทอีเมลอาจเป็น "จดหมายขยะ"

ตรงข้ามกับคลาสที่เป็นลบ

คลิกไอคอนเพื่อดูหมายเหตุเพิ่มเติม

คําว่าคลาสบวกอาจทําให้สับสนเนื่องจากผลลัพธ์ "บวก" ของหลายการทดสอบมักเป็นผลลัพธ์ที่ไม่พึงประสงค์ เช่น คลาสบวกในการตรวจทางการแพทย์หลายรายการจะสอดคล้องกับเนื้องอกหรือโรค โดยทั่วไปแล้ว คุณต้องการให้แพทย์บอกคุณว่า "ยินดีด้วย ผลตรวจของคุณเป็นลบ" อย่างไรก็ตาม คลาสเชิงบวกคือเหตุการณ์ที่การทดสอบพยายามค้นหา

คุณต้องยอมรับว่าคุณกําลังทดสอบทั้งคลาสเชิงบวกและเชิงลบพร้อมกัน

---

PR AUC (พื้นที่ใต้กราฟ PR)

#Metric

พื้นที่ใต้กราฟที่หาค่าเฉลี่ยระหว่างค่าต่างๆ ของกราฟ Precision-Recall ซึ่งหาได้จากการวางจุด (ความแม่นยำ ความแม่นยำ) สำหรับค่าต่างๆ ของเกณฑ์การจัดประเภท

ความแม่นยำ

#Metric

เมตริกสําหรับโมเดลการจัดหมวดหมู่ที่ตอบคำถามต่อไปนี้

เมื่อโมเดลคาดการณ์คลาสเชิงบวก การคาดการณ์ที่ถูกต้องมีเปอร์เซ็นต์เท่าใด

สูตรมีดังนี้

$$\text{Precision} = \frac{\text{true positives}} {\text{true positives} + \text{false positives}}$$

where:

• ผลบวกจริงหมายความว่าโมเดลคาดการณ์คลาสที่เป็นบวกได้ถูกต้อง
• ผลบวกลวงหมายความว่าโมเดลคาดการณ์คลาสที่เป็นบวกโดยไม่ได้ตั้งใจ

ตัวอย่างเช่น สมมติว่าโมเดลทำการคาดการณ์เชิงบวก 200 ครั้ง จากการคาดการณ์เชิงบวก 200 รายการนี้

• 150 รายการเป็นผลบวกจริง
• 50 รายการเป็นผลบวกลวง

ในกรณีนี้

$$\text{Precision} = \frac{\text{150}} {\text{150} + \text{50}} = 0.75$$

ตรงข้ามกับความแม่นยำและการจดจำ

ดูข้อมูลเพิ่มเติมได้ในการจัดประเภท: ความแม่นยำ การเรียกคืน ความแม่นยำ และเมตริกที่เกี่ยวข้องในหลักสูตรเร่งรัดเกี่ยวกับแมชชีนเลิร์นนิง

ความแม่นยำที่ k (precision@k)

#language

#Metric

เมตริกสําหรับประเมินรายการที่จัดอันดับ (เรียงลําดับ) ความแม่นยำที่ k จะระบุเศษส่วนของรายการ k รายการแรกในรายการนั้นซึ่ง "เกี่ยวข้อง" โดยการ

\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]

ค่าของ k ต้องน้อยกว่าหรือเท่ากับความยาวของลิสต์ที่แสดงผล โปรดทราบว่าความยาวของรายการที่แสดงผลไม่ได้เป็นส่วนหนึ่งของการคํานวณ

ความเกี่ยวข้องมักเป็นเรื่องส่วนตัว แม้แต่ผู้ประเมินที่เป็นมนุษย์ที่เชี่ยวชาญก็มักไม่เห็นด้วยว่ารายการใดมีความเกี่ยวข้อง

เปรียบเทียบกับ:

• ความแม่นยำเฉลี่ยที่ k
• ความแม่นยำเฉลี่ยของค่าเฉลี่ยที่ k

คลิกไอคอนเพื่อดูตัวอย่าง

สมมติว่าโมเดลภาษาขนาดใหญ่ได้รับคําค้นหาต่อไปนี้

List the 6 funniest movies of all time in order.

และโมเดลภาษาขนาดใหญ่จะแสดงรายการใน 2 คอลัมน์แรกของตารางต่อไปนี้

ตำแหน่ง	ภาพยนตร์	เกี่ยวข้องไหม
1	The General	ใช่
2	Mean Girls	ใช่
3	Platoon	ไม่
4	Bridesmaids	ใช่
5	Citizen Kane	ไม่
6	This is Spinal Tap	ใช่

ภาพยนตร์ 2 ใน 3 เรื่องแรกมีความเกี่ยวข้อง ความแม่นยำที่ 3 จึงเท่ากับ

$$\text{precision at 3} = \frac{\text{2}} {\text{3}} = 0.67$$

ภาพยนตร์ 4 ใน 5 เรื่องแรกมีความตลกมาก ความแม่นยำที่ 5 จึงเท่ากับ

$$\text{precision at 5} = \frac{\text{4}} {\text{5}} = 0.8$$

---

เส้นโค้ง Precision-Recall

#Metric

กราฟความแม่นยำเทียบกับความแม่นยำในการเรียกคืนที่เกณฑ์การจัดประเภทต่างๆ

อคติในการคาดการณ์

#Metric

ค่าที่ระบุระยะห่างระหว่างค่าเฉลี่ยของการคาดการณ์กับค่าเฉลี่ยของป้ายกํากับในชุดข้อมูล

โปรดอย่าสับสนกับคำที่เป็นอคติในโมเดลแมชชีนเลิร์นนิง หรืออคติด้านจริยธรรมและความเป็นธรรม

ความเท่าเทียมตามการคาดการณ์

#fairness

#Metric

เมตริกความเป็นธรรมที่ตรวจสอบว่าอัตราความแม่นยำของโปรแกรมแยกประเภทหนึ่งๆ เทียบเท่ากันสำหรับกลุ่มย่อยที่พิจารณาหรือไม่

เช่น โมเดลที่คาดการณ์การยอมรับเข้าวิทยาลัยจะต้องเป็นไปตามความเท่าเทียมในการคาดการณ์สำหรับสัญชาติหากอัตราความแม่นยำของโมเดลนั้นเหมือนกันสำหรับชาวลิลลี่ปุตและชาวบราบิงแนก

บางครั้งเราจะเรียกความเท่าเทียมตามการคาดการณ์ว่าความเท่าเทียมตามอัตราที่คาดการณ์

ดูการอภิปรายเรื่องความเท่าเทียมตามการคาดการณ์โดยละเอียดได้ที่"คำอธิบายความเท่าเทียม" (ส่วนที่ 3.2.1)

อัตราที่เท่ากันตามการคาดการณ์

#fairness

#Metric

อีกชื่อของความเท่าเทียมตามการคาดการณ์

ฟังก์ชันความหนาแน่นของความน่าจะเป็น

#Metric

ฟังก์ชันที่ระบุความถี่ของตัวอย่างข้อมูลที่มีค่าหนึ่งๆ ตรงกันทุกประการ เมื่อค่าของชุดข้อมูลเป็นตัวเลขทศนิยมต่อเนื่อง การจับคู่ที่ตรงกันทั้งหมดจะเกิดขึ้นน้อยมาก อย่างไรก็ตาม การผสานรวมฟังก์ชันความหนาแน่นความน่าจะเป็นจากค่า x ถึงค่า y จะให้ความถี่ที่คาดไว้ของตัวอย่างข้อมูลระหว่าง x ถึง y

ตัวอย่างเช่น พิจารณาการแจกแจงแบบปกติที่มีค่าเฉลี่ย 200 และค่าเบี่ยงเบนมาตรฐาน 30 หากต้องการระบุความถี่ที่คาดไว้ของตัวอย่างข้อมูลซึ่งอยู่ในช่วง 211.4 ถึง 218.7 ให้ผสานฟังก์ชันความหนาแน่นความน่าจะเป็นของการแจกแจงแบบปกติจาก 211.4 ถึง 218.7

R

การเรียกคืน

#Metric

เมตริกสําหรับโมเดลการจัดหมวดหมู่ที่ตอบคำถามต่อไปนี้

เมื่อข้อมูลจริงเป็นคลาสที่เป็นบวก เปอร์เซ็นต์การคาดการณ์ที่โมเดลระบุเป็นคลาสที่เป็นบวกอย่างถูกต้องคือเท่าใด

สูตรมีดังนี้

\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]

where:

• ผลบวกจริงหมายความว่าโมเดลคาดการณ์คลาสที่เป็นบวกได้ถูกต้อง
• ผลลบลวงหมายความว่าโมเดลคาดการณ์ผิดพลาดว่าคลาสเชิงลบ

ตัวอย่างเช่น สมมติว่าโมเดลของคุณทำการคาดการณ์ 200 ครั้งในตัวอย่างที่มีข้อมูลพื้นความจริงเป็นคลาสที่เป็นบวก จากการคาดการณ์ 200 รายการนี้

• 180 รายการเป็นผลบวกจริง
• 20 รายการเป็นผลลบลวง

ในกรณีนี้

\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]

คลิกไอคอนเพื่อดูหมายเหตุเกี่ยวกับชุดข้อมูลที่คลาสไม่สมดุล

ค่าการเรียกคืนมีประโยชน์อย่างยิ่งในการระบุความสามารถในการคาดการณ์ของโมเดลการจัดประเภทซึ่งมีคลาสที่เป็นบวกน้อย ตัวอย่างเช่น พิจารณาชุดข้อมูลที่ไม่สมดุลของคลาส ซึ่งคลาสบวกของโรคหนึ่งๆ เกิดขึ้นในผู้ป่วยเพียง 10 คนจาก 1 ล้านคน สมมติว่าโมเดลของคุณทำการคาดการณ์ 5 ล้านรายการซึ่งให้ผลลัพธ์ต่อไปนี้

• ผลบวกจริง 30 รายการ
• ผลลบลวง 20 รายการ
• ผลลบจริง 4,999,000 รายการ
• ผลบวกลวง 950 รายการ

ดังนั้นการเรียกคืนของรุ่นนี้จึงมีดังนี้

recall = TP / (TP + FN)
recall = 30 / (30 + 20) = 0.6 = 60%

ในทางตรงกันข้าม ความแม่นยำของโมเดลนี้คือ

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (30 + 4,999,000) / (30 + 4,999,000 + 950 + 20) = 99.98%

ค่าความถูกต้องที่สูงนั้นดูน่าประทับใจ แต่ไม่มีความหมายในทางปฏิบัติ ความแม่นยำเป็นเมตริกที่มีประโยชน์มากกว่าความแม่นยำสำหรับชุดข้อมูลที่ไม่สมดุลของคลาส

---

ดูข้อมูลเพิ่มเติมได้ที่การจัดประเภท: ความแม่นยำ การเรียกคืน ความแม่นยำ และเมตริกที่เกี่ยวข้อง

การจําที่ k (recall@k)

#language

#Metric

เมตริกสําหรับประเมินระบบที่แสดงรายการที่จัดอันดับ (เรียงลําดับ) การเรียกคืนที่ k จะระบุเศษส่วนของรายการที่เกี่ยวข้องในรายการ k รายการแรกในรายการนั้นจากจํานวนรายการที่เกี่ยวข้องทั้งหมดที่แสดง

\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]

เปรียบเทียบกับความแม่นยำที่ k

คลิกไอคอนเพื่อดูตัวอย่าง

สมมติว่าโมเดลภาษาขนาดใหญ่ได้รับคําค้นหาต่อไปนี้

List the 10 funniest movies of all time in order.

และโมเดลภาษาขนาดใหญ่จะแสดงรายการใน 2 คอลัมน์แรกดังนี้

ตำแหน่ง	ภาพยนตร์	เกี่ยวข้องไหม
1	The General	ใช่
2	Mean Girls	ใช่
3	Platoon	ไม่
4	Bridesmaids	ใช่
5	This is Spinal Tap	ใช่
6	เครื่องบิน	ใช่
7	Groundhog Day	ใช่
8	Monty Python and the Holy Grail	ใช่
9	Oppenheimer	ไม่
10	ไม่รู้	ใช่

ภาพยนตร์ 8 เรื่องในรายการก่อนหน้านี้ตลกมาก จึงถือเป็น "รายการที่เกี่ยวข้องในรายการ" ดังนั้น 8 จะเป็นตัวส่วนในการคํานวณการจําที่ k ทั้งหมด แล้วส่วนนําล่ะ รายการแรก 4 รายการมีความเกี่ยวข้อง 3 รายการ ดังนั้นการเรียกคืนที่ 4 คือ

$$\text{recall at 4} = \frac{\text{3}} {\text{8}} = 0.375$$

ภาพยนตร์ 7 ใน 8 เรื่องแรกเป็นเรื่องตลกมาก ดังนั้นการจําที่ 8 คือ

$$\text{recall at 8} = \frac{\text{7}} {\text{8}} = 0.875$$

---

เส้นโค้ง ROC (Receiver Operating Characteristic)

#fundamentals

#Metric

กราฟของอัตราผลบวกจริงเทียบกับอัตราผลบวกลวงสําหรับเกณฑ์การจัดประเภทแบบต่างๆ ในการจัดประเภทแบบไบนารี

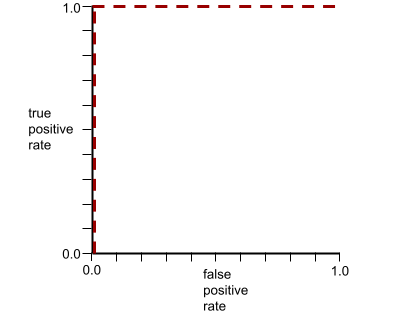
รูปร่างของเส้นโค้ง ROC บ่งบอกถึงความสามารถของโมเดลการจัดประเภทแบบไบนารีในการแยกคลาสที่เป็นบวกออกจากคลาสที่เป็นลบ ตัวอย่างเช่น สมมติว่าโมเดลการจัดประเภทแบบไบนารีแยกคลาสเชิงลบทั้งหมดออกจากคลาสเชิงบวกทั้งหมดได้อย่างสมบูรณ์

เส้นโค้ง ROC ของรูปแบบก่อนหน้ามีลักษณะดังนี้

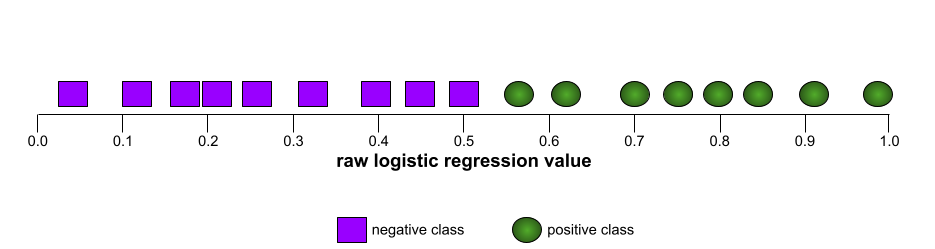
ในทางตรงกันข้าม ภาพประกอบต่อไปนี้แสดงกราฟค่าการถดถอยเชิงลอจิสติกส์ดิบสําหรับโมเดลที่ทํางานได้แย่มากซึ่งแยกคลาสเชิงลบออกจากคลาสเชิงบวกไม่ได้เลย

เส้นโค้ง ROC ของรูปแบบนี้จะมีลักษณะดังนี้

ในทางกลับกัน โมเดลการจัดประเภทแบบไบนารีส่วนใหญ่จะแยกคลาสที่เป็นบวกและลบในระดับหนึ่ง แต่มักจะไม่แยกได้อย่างสมบูรณ์ ดังนั้น กราฟ ROC ทั่วไปจึงอยู่ตรงกลางระหว่าง 2 ค่าสุดขั้วนี้

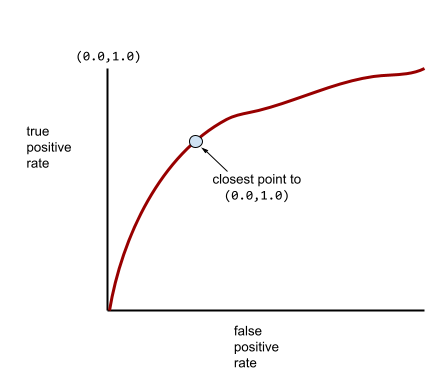
จุดบนเส้นโค้ง ROC ที่ใกล้กับ (0.0,1.0) มากที่สุดจะระบุเกณฑ์การแยกประเภทที่เหมาะสมในทางทฤษฎี อย่างไรก็ตาม ปัญหาอื่นๆ ที่เกิดขึ้นจริงหลายประการส่งผลต่อการเลือกเกณฑ์การจัดประเภทที่เหมาะสม ตัวอย่างเช่น ผลลบเท็จอาจทำให้เกิดปัญหามากกว่าผลบวกเท็จ

เมตริกตัวเลขที่เรียกว่า AUC จะสรุปเส้นโค้ง ROC เป็นค่าทศนิยมเดียว

ค่าเฉลี่ยความคลาดเคลื่อนกำลังสอง (RMSE)

#fundamentals

#Metric

รากที่สองของความคลาดเคลื่อนเฉลี่ยกำลังสอง

ROUGE (Recall-Oriented Understudy for Gisting Evaluation)

#language

#Metric

กลุ่มเมตริกที่ประเมินการสรุปอัตโนมัติและรูปแบบการแปลด้วยคอมพิวเตอร์ เมตริก ROUGE จะระบุระดับที่ข้อความอ้างอิงซ้อนทับกับข้อความที่สร้างขึ้นของโมเดล ML แต่ละสมาชิกของครอบครัว ROUGE จะวัดผลการซ้อนทับกันด้วยวิธีที่แตกต่างกัน คะแนน ROUGE ที่สูงกว่าบ่งชี้ว่าข้อความอ้างอิงกับข้อความที่สร้างขึ้นมีความคล้ายคลึงกันมากกว่าคะแนน ROUGE ที่ต่ำกว่า

โดยปกติแล้วสมาชิกในครอบครัว ROUGE แต่ละคนจะสร้างเมตริกต่อไปนี้

• ความแม่นยำ
• การจดจำ
• F₁

หมายเหตุ: ROUGE ใช้ความแม่นยำและความแม่นยำในการเรียกคืนแตกต่างจากความแม่นยำและความแม่นยำในการเรียกคืนแบบดั้งเดิม

ดูรายละเอียดและตัวอย่างได้ที่

• ROUGE-L
• ROUGE-N
• ROUGE-S

หมายเหตุ: BLEU และ BLEURT จะเพิ่มประสิทธิภาพเพื่อความแม่นยำ ส่วน ROUGE จะเพิ่มประสิทธิภาพเพื่อความครอบคลุม ดังนั้น BLEU และ BLEURT จึงเหมาะที่จะใช้เป็นเมตริกในการวัดการแปลด้วยคอมพิวเตอร์มากกว่า (เนื่องจากเน้นความแม่นยำ) ส่วน ROUGE เหมาะที่จะใช้เป็นเมตริกในการวัดการสรุปมากกว่า (เนื่องจากเน้นความแม่นยำในการเรียกคืน)

ROUGE-L

#language

#Metric

สมาชิกของตระกูล ROUGE ที่มุ่งเน้นที่ความยาวของอนุกรมย่อยที่พบร่วมกันยาวที่สุดในข้อความอ้างอิงและข้อความที่สร้างขึ้น สูตรต่อไปนี้จะคํานวณการเรียกคืนและความแม่นยําสําหรับ ROUGE-L

$$\text{ROUGE-L recall} = \frac{\text{longest common sequence}} {\text{number of words in the reference text} }$$

$$\text{ROUGE-L precision} = \frac{\text{longest common sequence}} {\text{number of words in the generated text} }$$

จากนั้นคุณสามารถใช้ F₁ เพื่อรวมการเรียกคืน ROUGE-L และแม่นยำของ ROUGE-L ไว้ในเมตริกเดียว ดังนี้

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{ROUGE-L recall} * \text{ROUGE-L precision}} {\text{ROUGE-L recall} + \text{ROUGE-L precision} }$$

คลิกไอคอนเพื่อดูตัวอย่างการคำนวณ ROUGE-L

พิจารณาข้อความอ้างอิงและข้อความที่สร้างขึ้นต่อไปนี้

หมวดหมู่	ใครเป็นโปรดิวเซอร์	ข้อความ
ข้อความอ้างอิง	นักแปล	ฉันต้องการทำความเข้าใจสิ่งต่างๆ มากมาย
ข้อความที่สร้างขึ้น	โมเดล ML	ฉันอยากเรียนรู้สิ่งต่างๆ มากมาย

ดังนั้น

• อนุกรมย่อยที่พบร่วมกันซึ่งมีความยาวที่สุดคือ 5 (I want to of things)
• จำนวนคำในข้อความอ้างอิงคือ 9
• จำนวนคำในข้อความที่สร้างขึ้นคือ 7

ดังนั้น

$$\text{ROUGE-L recall} = \frac{\text{5}} {\text{9} } = 0.56$$

$$\text{ROUGE-L precision} = \frac{\text{5}} {\text{7} } = 0.71$$

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{0.56} * \text{0.71}} {\text{0.56} + \text{0.71} } = 0.63$$

---

ROUGE-L ไม่สนใจการขึ้นบรรทัดใหม่ในข้อความอ้างอิงและข้อความที่สร้างขึ้น ดังนั้นอนุกรมย่อยที่พบร่วมกันยาวที่สุดอาจข้ามหลายประโยค เมื่อข้อความอ้างอิงและข้อความที่สร้างขึ้นมีประโยคหลายประโยค โดยทั่วไปแล้ว รูปแบบของ ROUGE-L ที่ชื่อ ROUGE-Lsum จะถือเป็นเมตริกที่ดีกว่า ROUGE-Lsum จะระบุอนุกรมย่อยที่พบร่วมกันยาวที่สุดสำหรับประโยคแต่ละประโยคในย่อหน้า จากนั้นจะคํานวณค่าเฉลี่ยของอนุกรมย่อยที่พบร่วมกันยาวที่สุดเหล่านั้น

คลิกไอคอนเพื่อดูตัวอย่างการคำนวณ ROUGE-Lsum

พิจารณาข้อความอ้างอิงและข้อความที่สร้างขึ้นต่อไปนี้

หมวดหมู่	ใครเป็นโปรดิวเซอร์	ข้อความ
ข้อความอ้างอิง	นักแปล	พื้นผิวของดาวอังคารแห้ง น้ำเกือบทั้งหมดอยู่ใต้ดิน
ข้อความที่สร้างขึ้น	โมเดล ML	ดาวอังคารมีพื้นผิวแห้ง แต่น้ำส่วนใหญ่อยู่ใต้ดิน

ดังนั้น

	ประโยคแรก	ประโยคที่ 2
ลำดับที่พบร่วมกันยาวที่สุด	2 (แห้งแบบดาวอังคาร)	3 (น้ำอยู่ใต้ดิน)
ความยาวของประโยคในข้อความอ้างอิง	6	7
ความยาวของประโยคในข้อความที่สร้างขึ้น	5	8

ด้วยเหตุนี้

$$\text{recall of first sentence} = \frac{\text{2}} {\text{6}} = 0.33 $$

$$\text{recall of second sentence} = \frac{\text{3}} {\text{7}} = 0.43 $$

$$\text{ROUGE-Lsum recall} = \frac{\text{0.33} + \text{0.43}} {\text{2}} = 0.38 $$

$$\text{precision of first sentence} = \frac{\text{2}} {\text{5}} = 0.4 $$

$$\text{precision of second sentence} = \frac{\text{3}} {\text{8}} = 0.38 $$

$$\text{ROUGE-Lsum precision} = \frac{\text{0.4} + \text{0.38}} {\text{2}} = 0.39 $$

$$\text{ROUGE-Lsum F}{_1} = \frac{\text{2} * \text{0.38} * \text{0.39}} {\text{0.38} + \text{0.39}} = 0.38 $$

---

ROUGE-N

#language

#Metric

ชุดเมตริกภายในตระกูล ROUGE ที่เปรียบเทียบ N-gram ที่ใช้ร่วมกันซึ่งมีขนาดที่แน่นอนในข้อความอ้างอิงและข้อความที่สร้างขึ้น เช่น

• ROUGE-1 จะวัดจํานวนโทเค็นที่ใช้ร่วมกันในข้อความอ้างอิงและข้อความที่สร้างขึ้น
• ROUGE-2 จะวัดจํานวน Bigram (2-gram) ที่แชร์ในข้อความอ้างอิงและข้อความที่สร้างขึ้น
• ROUGE-3 จะวัดจํานวน Trigram (3-gram) ที่แชร์ในข้อความอ้างอิงและข้อความที่สร้างขึ้น

คุณสามารถใช้สูตรต่อไปนี้เพื่อคํานวณการเรียกคืนและแม่นยําของ ROUGE-N สําหรับสมาชิกของตระกูล ROUGE-N

$$\text{ROUGE-N recall} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the reference text} }$$

$$\text{ROUGE-N precision} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the generated text} }$$

จากนั้นคุณสามารถใช้ F₁ เพื่อรวมการเรียกคืน ROUGE-N และแม่นยำของ ROUGE-N ไว้ในเมตริกเดียว ดังนี้

$$\text{ROUGE-N F}{_1} = \frac{\text{2} * \text{ROUGE-N recall} * \text{ROUGE-N precision}} {\text{ROUGE-N recall} + \text{ROUGE-N precision} }$$

คลิกไอคอนเพื่อดูตัวอย่าง

สมมติว่าคุณตัดสินใจใช้ ROUGE-2 เพื่อวัดประสิทธิภาพของคำแปลจากโมเดล ML เทียบกับคำแปลจากนักแปลที่เป็นมนุษย์

หมวดหมู่	ใครเป็นโปรดิวเซอร์	ข้อความ	Bigram
ข้อความอ้างอิง	นักแปล	ฉันต้องการทำความเข้าใจสิ่งต่างๆ มากมาย	ฉันต้องการ ต้องการที่จะ ทำความเข้าใจ ทำความเข้าใจเรื่องต่างๆ มากมาย
ข้อความที่สร้างขึ้น	โมเดล ML	ฉันอยากเรียนรู้สิ่งต่างๆ มากมาย	ฉันอยาก, อยากที่จะ, เรียนรู้, เรียนรู้สิ่งต่างๆ มากมาย

ดังนั้น

• จํานวน 2-gram ที่ตรงกันคือ 3 (I want, want to และof things)
• จำนวน 2-gram ในข้อความอ้างอิงคือ 8
• จำนวน 2-gram ในข้อความที่สร้างขึ้นคือ 6

ดังนั้น

$$\text{ROUGE-2 recall} = \frac{\text{3}} {\text{8} } = 0.375$$

$$\text{ROUGE-2 precision} = \frac{\text{3}} {\text{6} } = 0.5$$

$$\text{ROUGE-2 F}{_1} = \frac{\text{2} * \text{0.375} * \text{0.5}} {\text{0.375} + \text{0.5} } = 0.43$$

---

ROUGE-S

#language

#Metric

รูปแบบที่ยืดหยุ่นของ ROUGE-N ที่เปิดใช้การจับคู่ Skip-Gram กล่าวคือ ROUGE-N จะนับเฉพาะ N-gram ที่ตรงกันทุกประการ แต่ ROUGE-S จะนับ N-gram ที่แยกกันด้วยคำอย่างน้อย 1 คำด้วย เช่น โปรดคำนึงถึงสิ่งต่อไปนี้

• reference text: White clouds
• ข้อความที่สร้างขึ้น: เมฆสีขาวที่ลอยอยู่

เมื่อคํานวณ ROUGE-N 2-gram White clouds ไม่ตรงกับ White billowing clouds อย่างไรก็ตาม เมื่อคำนวณ ROUGE-S คำว่าเมฆสีขาวจะตรงกับเมฆสีขาวที่ลอยอยู่

R-squared

#Metric

เมตริกการถดถอยที่ระบุความแปรปรวนของป้ายกํากับที่เกิดจากฟีเจอร์แต่ละรายการหรือชุดฟีเจอร์ ค่า R-squared คือค่าระหว่าง 0 ถึง 1 ซึ่งคุณตีความได้ดังนี้

• ค่า R-squared เท่ากับ 0 หมายความว่าความแปรปรวนของป้ายกำกับไม่ได้เกิดจากชุดฟีเจอร์
• ค่า R-squared เท่ากับ 1 หมายความว่าความแปรปรวนทั้งหมดของป้ายกํากับเกิดจากชุดฟีเจอร์
• ค่า R-squared ระหว่าง 0 ถึง 1 บ่งบอกถึงระดับที่ความหลากหลายของป้ายกำกับสามารถคาดการณ์ได้จากฟีเจอร์หนึ่งๆ หรือชุดฟีเจอร์ เช่น ค่า R ยกกำลังสอง 0.10 หมายความว่าความแปรปรวน 10 เปอร์เซ็นต์ในป้ายกำกับนั้นเกิดจากชุดฟีเจอร์ ค่า R ยกกำลังสอง 0.20 หมายความว่า 20 เปอร์เซ็นต์นั้นเกิดจากชุดฟีเจอร์ และอื่นๆ

ค่า R ยกกำลังสองคือค่ากำลังสองของสัมประสิทธิ์สหสัมพันธ์ของ Pearson ระหว่างค่าที่โมเดลคาดการณ์ไว้กับข้อมูลจากการสังเกตการณ์โดยตรง

S

การให้คะแนน

#recsystems

#Metric

ส่วนหนึ่งของระบบการแนะนำที่ให้ค่าหรือการจัดอันดับสำหรับรายการแต่ละรายการที่สร้างขึ้นจากระยะการสร้างผู้สมัคร

การวัดความคล้ายคลึง

#clustering

#Metric

ในอัลกอริทึมการจัดกลุ่ม เมตริกที่ใช้เพื่อระบุความคล้ายคลึงกัน (ความคล้ายกัน) ของตัวอย่าง 2 รายการ

การขาดแคลนข้อมูล

#Metric

จํานวนองค์ประกอบที่ตั้งค่าเป็น 0 (หรือ Null) ในเวกเตอร์หรือเมทริกซ์หารด้วยจํานวนรายการทั้งหมดในเวกเตอร์หรือเมทริกซ์นั้น ตัวอย่างเช่น ลองพิจารณาเมทริกซ์ที่มีองค์ประกอบ 100 รายการ ซึ่ง 98 เซลล์มีค่าเป็น 0 การคำนวณความถี่ต่ำมีดังนี้

$$ {\text{sparsity}} = \frac{\text{98}} {\text{100}} = {\text{0.98}} $$

ความถี่ต่ำของฟีเจอร์หมายถึงความถี่ต่ำของเวกเตอร์ฟีเจอร์ ส่วนความถี่ต่ำของโมเดลหมายถึงความถี่ต่ำของน้ำหนักโมเดล

ผลรวมของการสูญเสียบานพับกำลังสอง

#Metric

ผลคูณของ การสูญเสียจากการเปิด/ปิด ผลรวมของการสูญเสียแบบสี่เหลี่ยมจัตุรัสจะลงโทษค่าที่ผิดปกติรุนแรงกว่าผลรวมของการสูญเสียแบบปกติ

ผลรวมของค่าสัมบูรณ์ของข้อผิดพลาด

#fundamentals

#Metric

คำพ้องความหมายของการสูญเสีย L₂

T

การสูญเสียในการทดสอบ

#fundamentals

#Metric

เมตริกที่แสดงถึงการสูญเสียของโมเดลเทียบกับชุดทดสอบ เมื่อสร้างโมเดล คุณมักจะพยายามลดการสูญเสียในการทดสอบ เนื่องจากการสูญเสียในการทดสอบที่ต่ำเป็นสัญญาณคุณภาพที่ชัดเจนกว่าการสูญเสียในการฝึกที่ต่ำหรือการสูญเสียในการทดสอบที่ต่ำ

บางครั้งช่องว่างระหว่างการสูญเสียในชุดทดสอบกับการสูญเสียในชุดฝึกหรือชุดตรวจสอบที่มากอาจบ่งบอกว่าคุณต้องเพิ่มอัตราการปรับสมดุล

ความแม่นยำของ Top-K

#language

#Metric

เปอร์เซ็นต์ของเวลาที่ "ป้ายกำกับเป้าหมาย" ปรากฏในตำแหน่ง k แรกๆ ของรายการที่สร้างขึ้น รายการอาจเป็นคําแนะนําที่ปรับเปลี่ยนในแบบของคุณ หรือรายการสินค้าที่จัดเรียงตาม softmax

ความแม่นยำของ Top-k เรียกอีกอย่างว่าความแม่นยำที่ k

หมายเหตุ: ป้ายกํากับเป้าหมายอาจเป็นคลาสใดก็ได้ (ไม่จําเป็นต้องเป็นคลาสข้อมูลจริง) ดังนั้นความถูกต้องของ Top-K จึงไม่ได้เท่ากับความถูกต้องแบบดั้งเดิมเสมอไป

คลิกไอคอนเพื่อดูตัวอย่าง

ลองพิจารณาระบบแมชชีนเลิร์นนิงที่ใช้ Softmax เพื่อระบุความน่าจะเป็นของต้นไม้ตามรูปภาพใบไม้ ตารางต่อไปนี้แสดงรายการเอาต์พุตที่สร้างขึ้นจากรูปภาพต้นไม้อินพุต 5 รูป แต่ละแถวจะมีป้ายกำกับเป้าหมายและต้นไม้ที่เป็นไปได้มากที่สุด 5 ต้น ตัวอย่างเช่น เมื่อป้ายกำกับเป้าหมายคือmaple โมเดลแมชชีนเลิร์นนิงจะระบุelm เป็นต้นไม้ที่เป็นไปได้มากที่สุด oak เป็นต้นไม้ที่เป็นไปได้มากที่สุดเป็นอันดับ 2 และอื่นๆ

ป้ายกํากับเป้าหมาย	1	2	3	4	5
เมเปิล	เอล์ม	โอ๊ก	maple	บีช	พอปลาร์
ด็อกวู้ด	โอ๊ก	dogwood	พอปลาร์	Hickory	เมเปิล
โอ๊ก	oak	ไม้เบิร์ช	ตั๊กแตน	เอลเดอร์	Linden
Linden	เมเปิล	paw-paw	โอ๊ก	ไม้เบิร์ช	พอปลาร์
โอ๊ก	ตั๊กแตน	Linden	oak	เมเปิล	paw-paw

ป้ายกํากับเป้าหมายปรากฏในตําแหน่งแรกเพียงครั้งเดียว ความแม่นยําของ Top-1 จึงเท่ากับ

$$\text{top-1 accuracy} = \frac{\text{1}} {\text{5}} = 0.2$$

ป้ายกํากับเป้าหมายปรากฏในตําแหน่งใดตําแหน่งหนึ่งใน 3 อันดับแรก 4 ครั้ง ดังนั้นความแม่นยําของ 3 อันดับแรกจึงเท่ากับ

$$\text{top-1 accuracy} = \frac{\text{4}} {\text{5}} = 0.8$$

---

ความเชื่อผิดๆ

#language

#Metric

ระดับที่เนื้อหาเป็นการละเมิด ข่มขู่ หรือทำให้เกิดความไม่พอใจ โมเดลแมชชีนเลิร์นนิงจำนวนมากสามารถระบุและวัดระดับความเป็นพิษได้ โมเดลส่วนใหญ่เหล่านี้จะระบุความเป็นพิษตามพารามิเตอร์หลายรายการ เช่น ระดับภาษาที่ไม่เหมาะสมและระดับภาษาที่เป็นภัย

การสูญเสียจากการฝึก

#fundamentals

#Metric

เมตริกที่แสดงถึงการสูญเสียของโมเดลระหว่างการทำซ้ำการฝึกหนึ่งๆ เช่น สมมติว่าฟังก์ชันการสูญเสียคือความคลาดเคลื่อนกำลังสองเฉลี่ย ตัวอย่างเช่น การสูญเสียในการฝึก (ข้อผิดพลาดค่าเฉลี่ยสี่เหลี่ยมจัตุรัส) ของการทำซ้ำครั้งที่ 10 คือ 2.2 และการสูญเสียในการฝึกของการทำซ้ำครั้งที่ 100 คือ 1.9

เส้นโค้งการสูญเสียจะแสดงการลดลงของการฝึกเทียบกับจํานวนการวนซ้ำ เส้นโค้งการสูญเสียจะให้คำแนะนำต่อไปนี้เกี่ยวกับการฝึก

• เส้นที่ลาดลงหมายความว่าโมเดลมีประสิทธิภาพดีขึ้น
• เส้นลาดขึ้นหมายความว่าโมเดลมีประสิทธิภาพแย่ลง
• เส้นลาดชันที่ราบเรียบหมายความว่าโมเดลบรรลุการบรรจบแล้ว

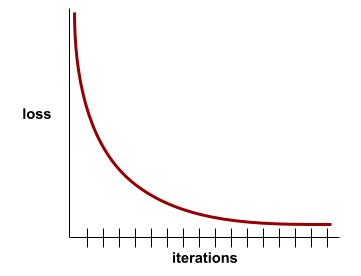
ตัวอย่างเช่น เส้นโค้งการสูญเสียต่อไปนี้ซึ่งค่อนข้างเป็นอุดมคติจะแสดงข้อมูลต่อไปนี้

• เส้นลาดลงชันในช่วงการทำซ้ำครั้งแรก ซึ่งหมายความว่าโมเดลได้รับการปรับปรุงอย่างรวดเร็ว
• เส้นลาดชันที่ค่อยๆ ราบลง (แต่ยังคงลดลง) จนใกล้ถึงช่วงสิ้นสุดการฝึก ซึ่งหมายความว่ามีการปรับปรุงโมเดลอย่างต่อเนื่องในอัตราที่ช้ากว่าช่วงการทำซ้ำครั้งแรก
• เส้นลาดชันที่ราบเรียบในช่วงท้ายของการฝึก ซึ่งบ่งบอกถึงการบรรจบ

แม้ว่าการสูญเสียระหว่างการฝึกจะมีความสำคัญ แต่โปรดดูการทั่วไปด้วย

ผลลบจริง (TN)

#fundamentals

#Metric

ตัวอย่างที่โมเดลคาดการณ์คลาสเชิงลบได้อย่างถูกต้อง ตัวอย่างเช่น โมเดลอนุมานว่าข้อความอีเมลหนึ่งๆ ไม่ใช่จดหมายขยะ และข้อความอีเมลนั้นไม่ใช่จดหมายขยะจริงๆ

ผลบวกจริง (TP)

#fundamentals

#Metric

ตัวอย่างที่โมเดลคาดการณ์คลาสที่เป็นบวกได้อย่างถูกต้อง เช่น โมเดลอนุมานว่าข้อความอีเมลหนึ่งๆ เป็นจดหมายขยะ และข้อความอีเมลนั้นจริงๆ แล้วเป็นจดหมายขยะ

อัตราผลบวกจริง (TPR)

#fundamentals

#Metric

คำพ้องความหมายของ recall โดยการ

$$\text{true positive rate} = \frac {\text{true positives}} {\text{true positives} + \text{false negatives}}$$

อัตราผลบวกจริงคือแกน y ในกราฟ ROC

V

การสูญเสียการตรวจสอบ

#fundamentals

#Metric

เมตริกที่แสดงถึงความสูญเสียของโมเดลในชุดทดสอบระหว่างการทำซ้ำการฝึกหนึ่งๆ

โปรดดูเส้นโค้งทั่วไปด้วย

ความสำคัญของตัวแปร

#df

#Metric

ชุดคะแนนที่ระบุความสำคัญแบบสัมพัทธ์ของฟีเจอร์แต่ละรายการต่อโมเดล

เช่น ลองพิจารณาแผนภูมิการตัดสินใจซึ่งประเมินราคาบ้าน สมมติว่าแผนผังการตัดสินใจนี้ใช้ฟีเจอร์ 3 อย่าง ได้แก่ ขนาด อายุ และสไตล์ หากชุดความสำคัญของตัวแปรสำหรับฟีเจอร์ 3 รายการคำนวณออกมาเป็น {size=5.8, age=2.5, style=4.7} แสดงว่าขนาดมีความสําคัญต่อต้นไม้การตัดสินใจมากกว่าอายุหรือสไตล์

เมตริกความสำคัญของตัวแปรต่างๆ มีอยู่ ซึ่งสามารถให้ข้อมูลแก่ผู้เชี่ยวชาญด้าน ML เกี่ยวกับแง่มุมต่างๆ ของโมเดล

W

การสูญเสีย Wasserstein

#Metric

ฟังก์ชันการสูญเสียอย่างหนึ่งที่ใช้กันโดยทั่วไปในเครือข่าย Generative Adversarial ซึ่งอิงตามระยะทาง Earth Mover's Distance ระหว่างการแจกแจงของข้อมูลที่สร้างขึ้นกับข้อมูลจริง