โมดูลนี้จะแนะนําแนวคิดการถดถอยเชิงเส้น
การถดถอยเชิงเส้นเป็น เทคนิคทางสถิติที่ใช้เพื่อหาความสัมพันธ์ระหว่างตัวแปร ในการเรียนรู้ของเครื่อง (ML) การถดถอยเชิงเส้นจะค้นหาความสัมพันธ์ระหว่าง ฟีเจอร์และ ป้ายกำกับ
ตัวอย่างเช่น สมมติว่าเราต้องการคาดการณ์ประสิทธิภาพการใช้เชื้อเพลิงของรถยนต์เป็นไมล์ต่อแกลลอนตามน้ำหนักของรถยนต์ และเรามีชุดข้อมูลต่อไปนี้
| ปอนด์ในหน่วยพัน (ฟีเจอร์) | ไมล์ต่อแกลลอน (ป้ายกำกับ) |
|---|---|
| 3.5 | 18 |
| 3.69 | 15 |
| 3.44 | 18 |
| 3.43 | 16 |
| 4.34 | 15 |
| 4.42 | 14 |
| 2.37 | 24 |
หากเราพล็อตจุดเหล่านี้ เราจะได้กราฟต่อไปนี้
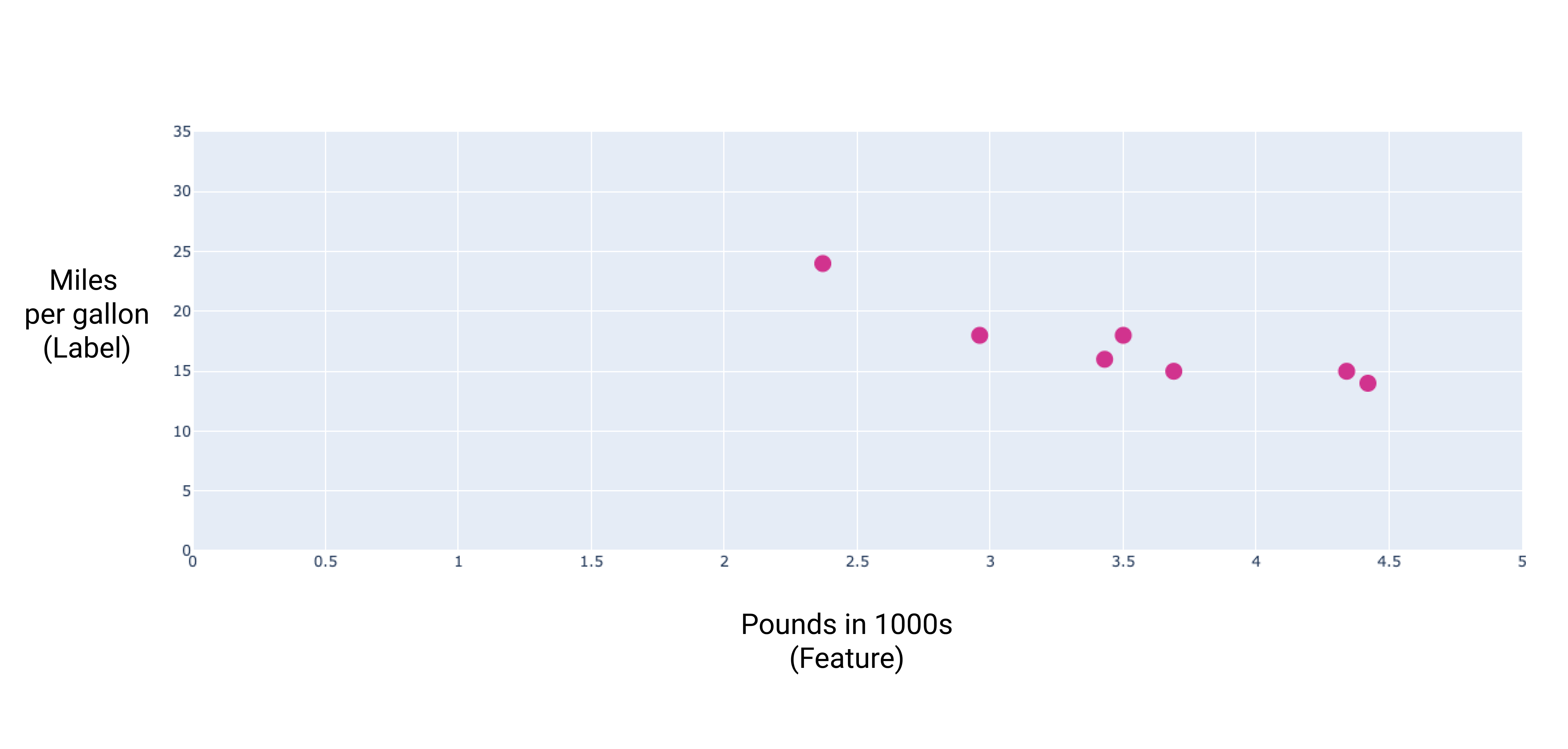
รูปที่ 1 ความหนักของรถ (เป็นปอนด์) เทียบกับอัตราการสิ้นเปลืองน้ำมันเป็นไมล์ต่อแกลลอน โดยทั่วไปแล้ว เมื่อรถยนต์มีน้ำหนักมากขึ้น อัตราการประหยัดน้ำมันต่อแกลลอนก็จะลดลง
เราสามารถสร้างโมเดลของเราเองได้โดยการลากเส้นแนวโน้มที่เหมาะสมที่สุดผ่านจุดต่างๆ ดังนี้
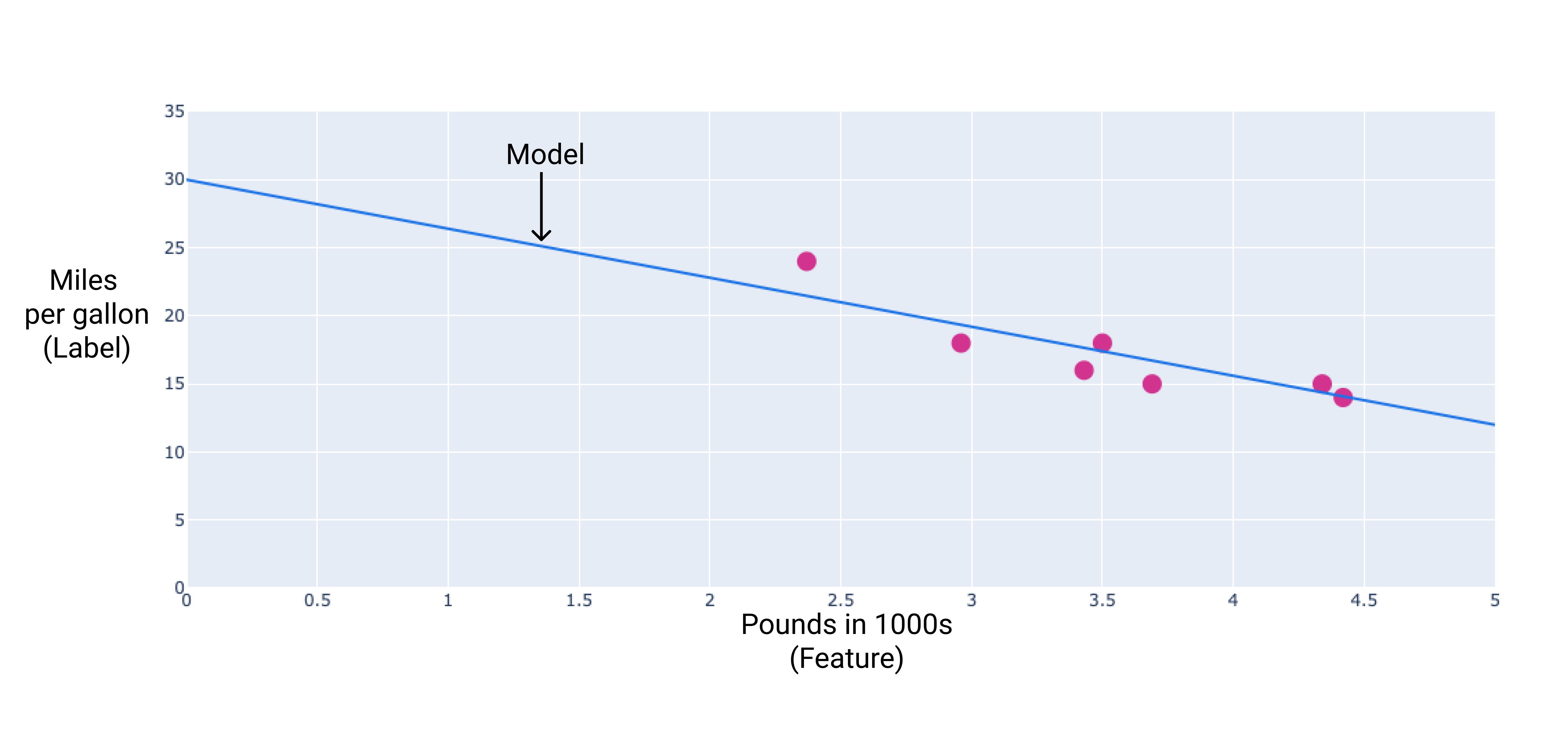
รูปที่ 2 เส้นแนวโน้มที่ลากผ่านข้อมูลจากรูปก่อนหน้า
สมการการถดถอยเชิงเส้น
ในเชิงพีชคณิต โมเดลจะกำหนดเป็น $ y = mx + b $ โดยที่
- $ y $ คือไมล์ต่อแกลลอน ซึ่งเป็นค่าที่เราต้องการคาดการณ์
- $ m $ คือความชันของเส้น
- $ x $ คือปอนด์ ซึ่งเป็นค่าอินพุต
- $ b $ คือจุดตัดแกน y
ใน ML เราเขียนสมการสำหรับโมเดลการถดถอยเชิงเส้นดังนี้
โดย
- $ y' $ คือป้ายกำกับที่คาดการณ์ไว้ ซึ่งเป็นเอาต์พุต
- $ b $ คืออคติ ของโมเดล อคติเป็นแนวคิดเดียวกับจุดตัดแกน y ในสมการพีชคณิต สำหรับเส้นตรง ใน ML บางครั้งอคติจะเรียกว่า $ w_0 $ อคติ คือพารามิเตอร์ของโมเดลและ จะคำนวณระหว่างการฝึก
- $ w_1 $ คือน้ำหนักของฟีเจอร์ น้ำหนักมีแนวคิดเดียวกับความชัน $ m $ ในสมการพีชคณิต สำหรับเส้น น้ำหนักเป็นพารามิเตอร์ของโมเดลและจะ คำนวณระหว่างการฝึก
- $ x_1 $ คือฟีเจอร์ ซึ่งเป็นอินพุต
ระหว่างการฝึก โมเดลจะคำนวณน้ำหนักและอคติที่สร้างโมเดลที่ดีที่สุด
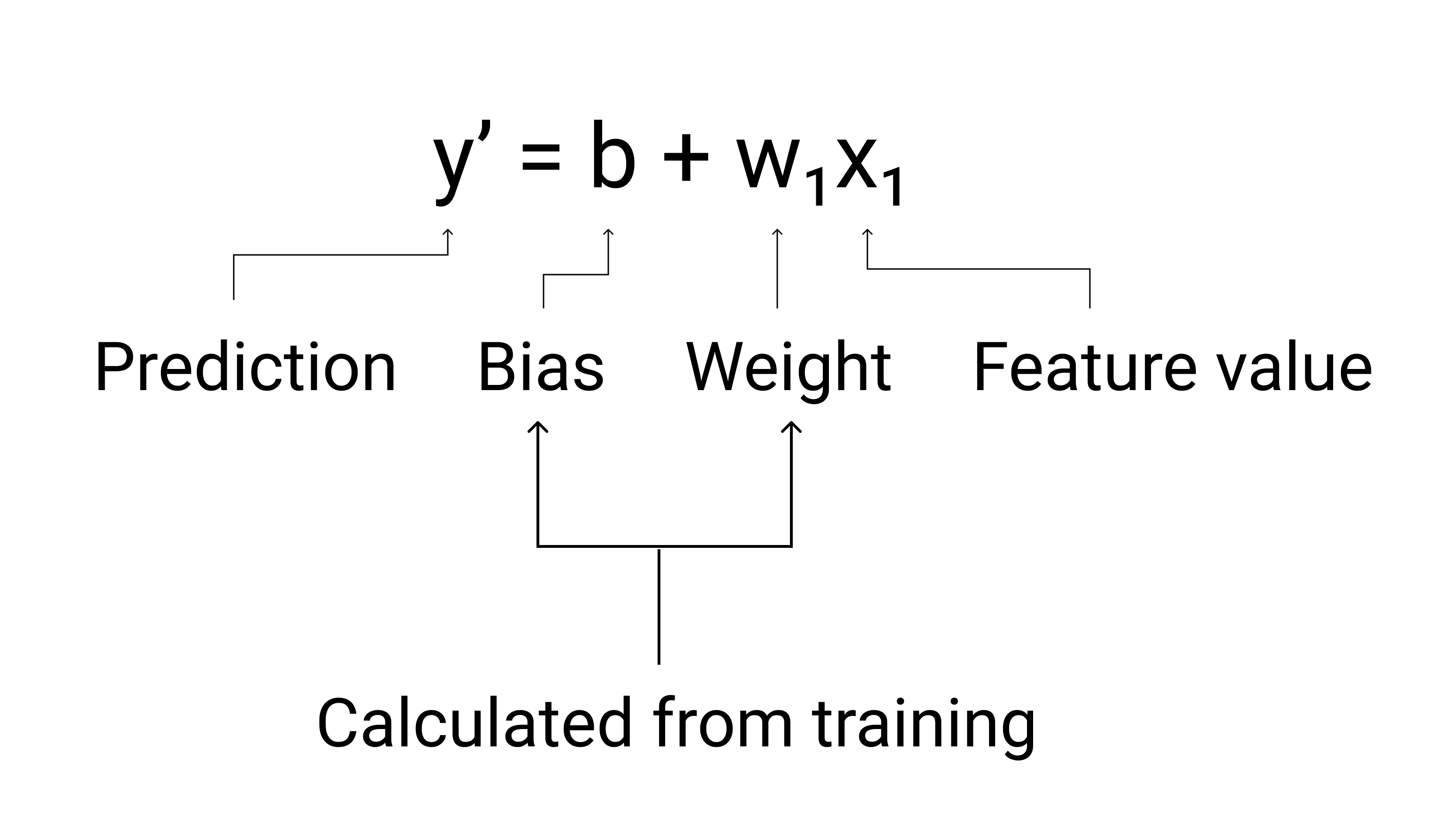
รูปที่ 3 การแสดงรูปแบบเชิงเส้นในทางคณิตศาสตร์
ในตัวอย่างของเรา เราจะคำนวณน้ำหนักและอคติจากเส้นที่เราวาด อคติคือ 34 (จุดที่เส้นตัดแกน y) และน้ำหนักคือ -4.6 (ความชันของเส้น) เราจะกำหนดโมเดลเป็น $ y' = 34 + (-4.6)(x_1) $ และ ใช้เพื่อทำการคาดการณ์ได้ ตัวอย่างเช่น เมื่อใช้โมเดลนี้ รถยนต์ที่มีน้ำหนัก 4,000 ปอนด์จะมีประสิทธิภาพการใช้เชื้อเพลิงที่คาดการณ์ไว้ 15.6 ไมล์ต่อแกลลอน
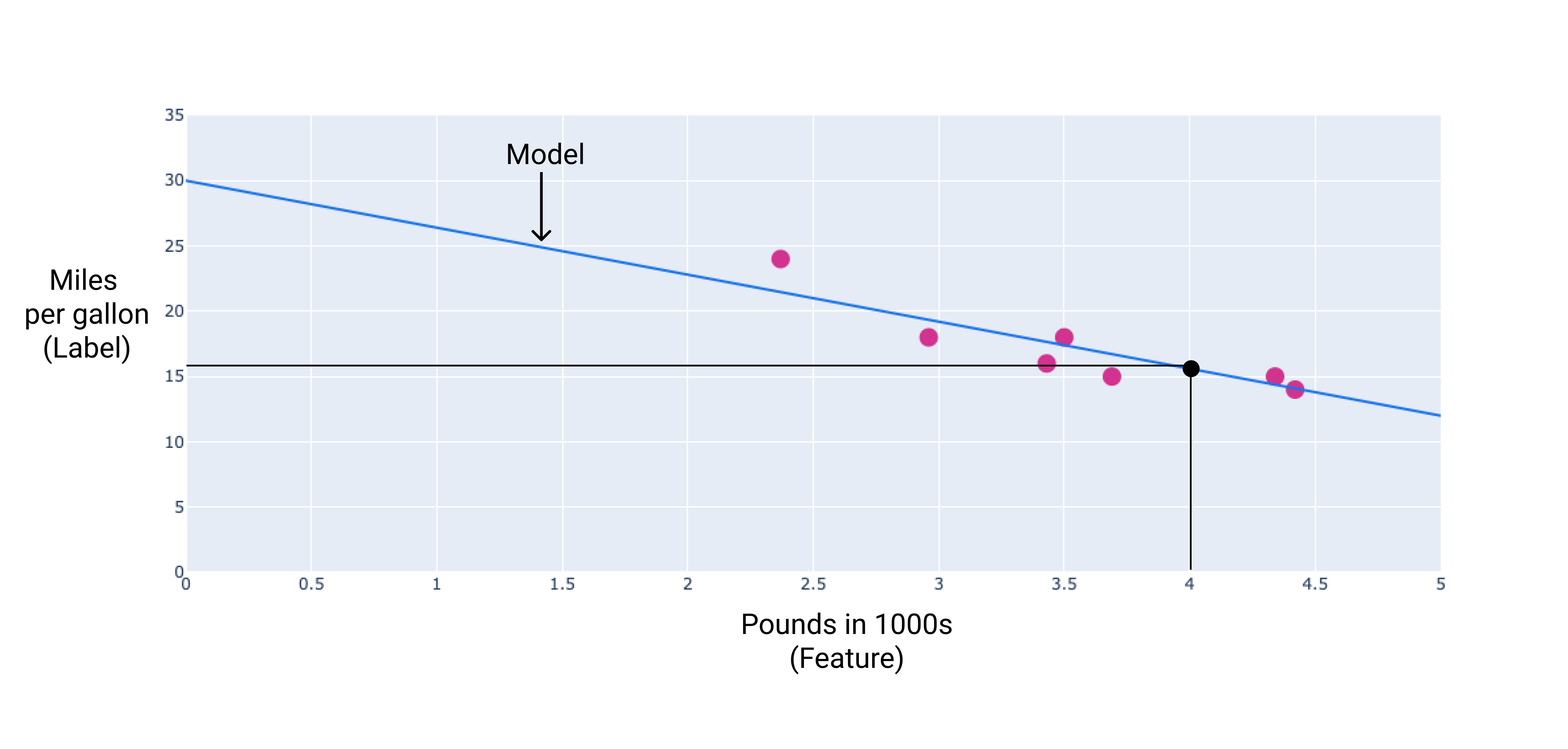
รูปที่ 4 รถยนต์ที่มีน้ำหนัก 4,000 ปอนด์จะมีอัตราการสิ้นเปลืองเชื้อเพลิงที่คาดการณ์ไว้ที่ 15.6 ไมล์ต่อแกลลอนเมื่อใช้โมเดล
โมเดลที่มีฟีเจอร์หลายอย่าง
แม้ว่าตัวอย่างในส่วนนี้จะใช้ฟีเจอร์เดียวเท่านั้น นั่นคือความหนักของรถ แต่โมเดลที่ซับซ้อนกว่าอาจต้องอาศัยฟีเจอร์หลายอย่าง โดยแต่ละฟีเจอร์จะมีน้ำหนักแยกกัน ($ w_1 $, $ w_2 $ ฯลฯ) เช่น โมเดล ที่อิงตามฟีเจอร์ 5 รายการจะเขียนได้ดังนี้
$ y' = b + w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + w_5x_5 $
ตัวอย่างเช่น โมเดลที่คาดการณ์อัตราการสิ้นเปลืองน้ำมันอาจใช้ฟีเจอร์เพิ่มเติม เช่น
- ความจุเครื่องยนต์
- การเร่งความเร็ว
- จำนวนกระบอกสูบ
- แรงม้า
โมเดลนี้จะเขียนได้ดังนี้
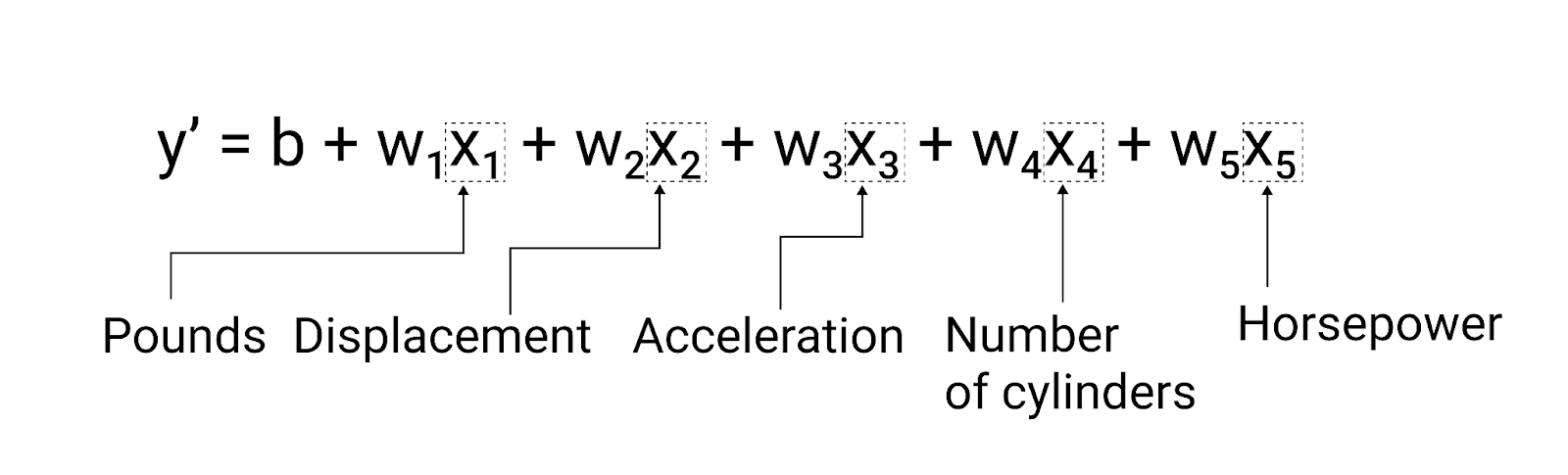
รูปที่ 5 โมเดลที่มีฟีเจอร์ 5 รายการเพื่อคาดการณ์การจัดอันดับไมล์ต่อแกลลอนของรถยนต์
เมื่อสร้างกราฟของฟีเจอร์เพิ่มเติม 2-3 รายการนี้ เราจะเห็นว่าฟีเจอร์เหล่านี้มีความสัมพันธ์เชิงเส้นกับป้ายกำกับไมล์ต่อแกลลอนด้วย
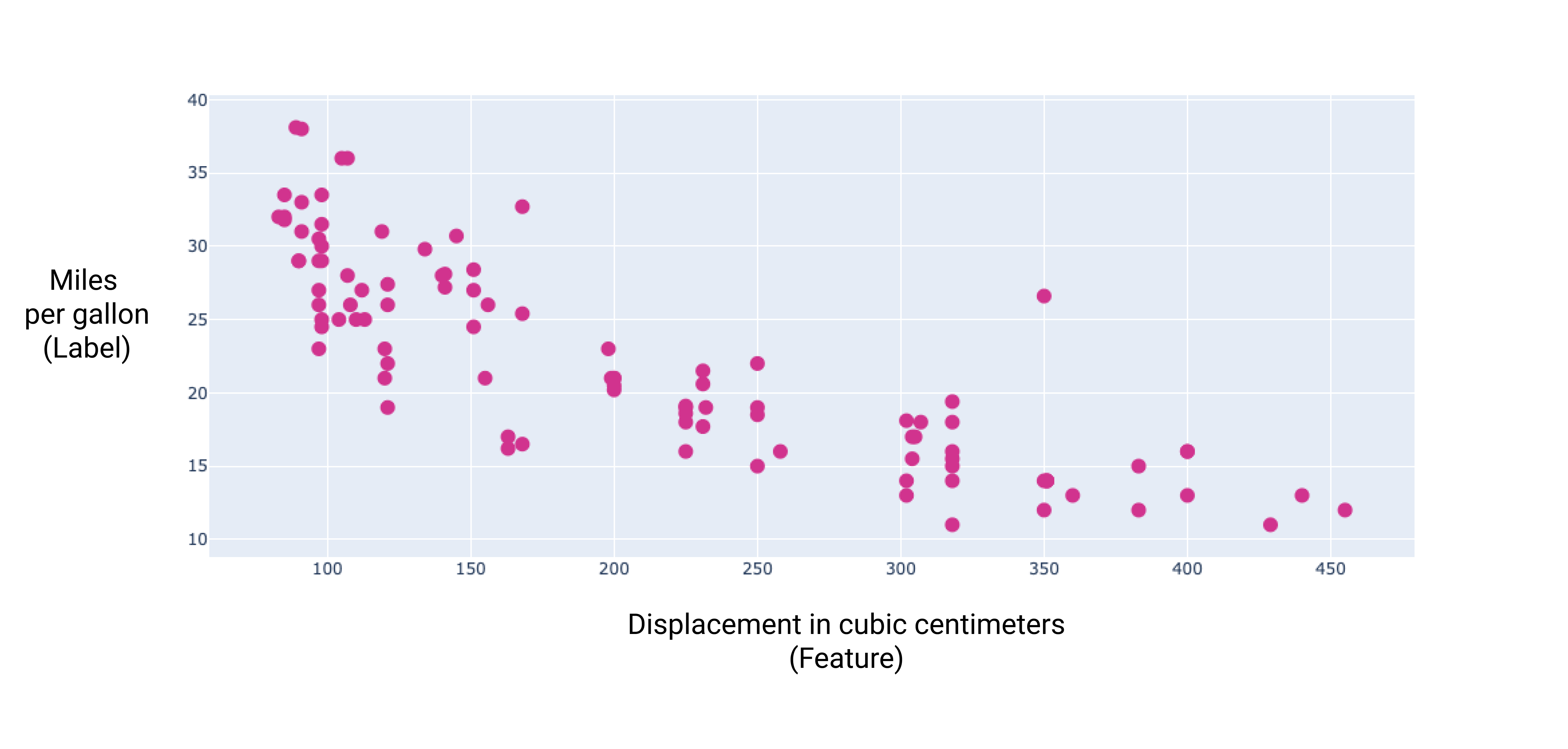
รูปที่ 6 ความจุกระบอกสูบของรถยนต์ในหน่วยลูกบาศก์เซนติเมตรและอัตราการสิ้นเปลืองเชื้อเพลิงในหน่วยไมล์ต่อแกลลอน เมื่อเครื่องยนต์ของรถยนต์มีขนาดใหญ่ขึ้น โดยทั่วไปแล้วอัตราการประหยัดน้ำมันต่อแกลลอนจะ ลดลง
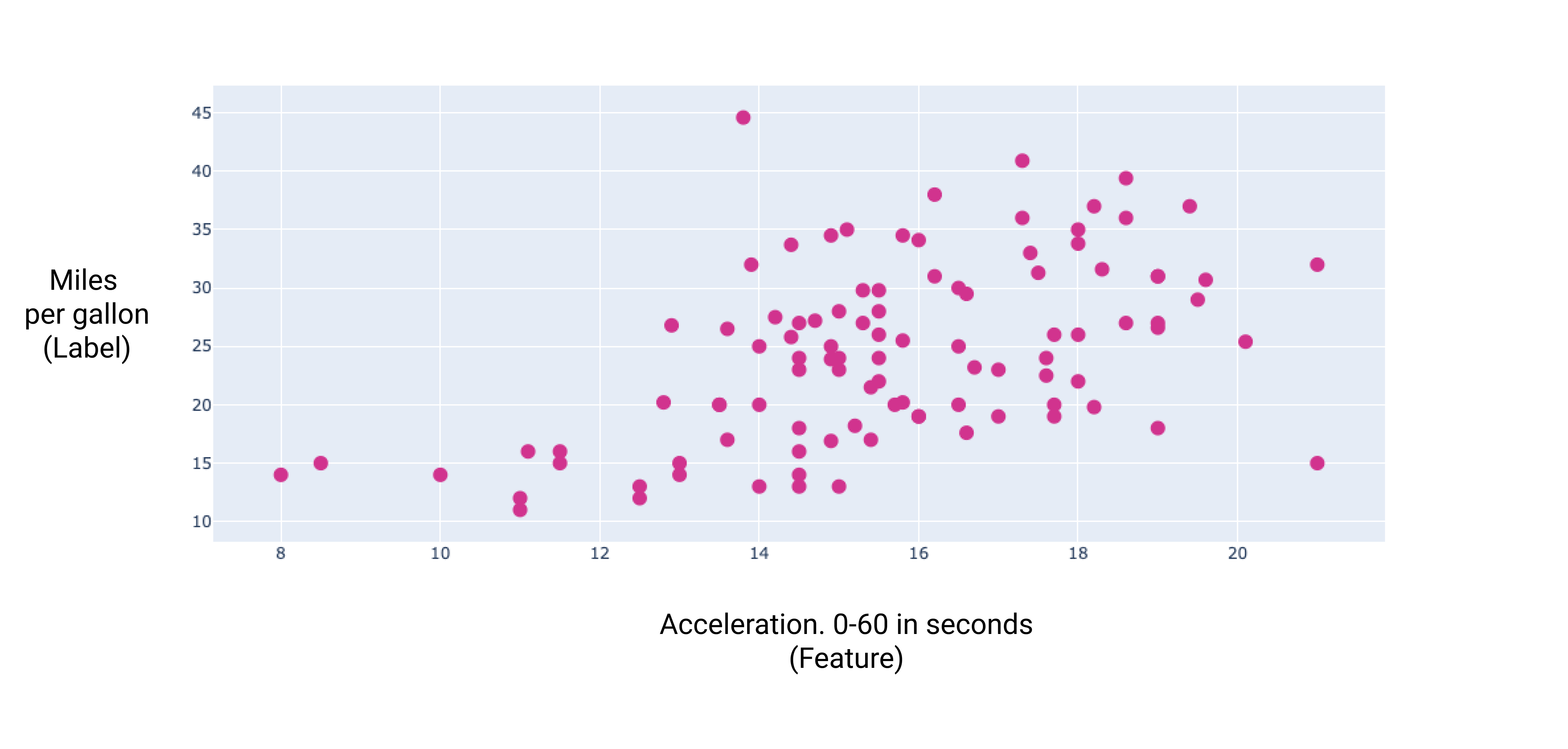
รูปที่ 7 อัตราเร่งและอัตราสิ้นเปลืองน้ำมันเชื้อเพลิงไมล์ต่อแกลลอนของรถยนต์ โดยทั่วไปแล้ว เมื่อรถยนต์ เร่งความเร็วได้ช้าลง อัตราการประหยัดน้ำมันต่อแกลลอนก็จะเพิ่มขึ้น
