Pièges d'analyse

"Tous les modèles sont faux, mais certains sont utiles." — George Box, 1978

Bien qu'efficaces, les techniques statistiques présentent certaines limites. Comprendre ces limites peut aider un chercheur à éviter les gaffes et les affirmations inexactes, comme l'affirmation de BF Skinner selon laquelle Shakespeare n'utilisait pas l'allitération plus que le hasard ne le prévoyait. (L'étude de Skinner était insuffisante.¹)

Incertitude et barres d'erreur

Il est important de spécifier l'incertitude dans votre analyse. Il est tout aussi important de quantifier l'incertitude dans les analyses d'autres personnes. Les points de données qui semblent tracer une tendance sur un graphique, mais dont les barres d'erreur se chevauchent, peuvent ne pas indiquer de tendance du tout. L'incertitude peut également être trop élevée pour tirer des conclusions utiles d'une étude ou d'un test statistique particulier. Si une étude de recherche nécessite une précision au niveau du lot, un ensemble de données géospatiales avec une incertitude de +/- 500 m est trop incertain pour être utilisable.

Les niveaux d'incertitude peuvent également être utiles lors des processus de prise de décision. Les données étayant un traitement de l'eau particulier avec une incertitude de 20% sur les résultats peuvent conduire à une recommandation d'implémentation de ce traitement de l'eau, avec un suivi continu du programme pour résoudre cette incertitude.

Les réseaux de neurones bayésiens peuvent quantifier l'incertitude en prédisant des distributions de valeurs plutôt que des valeurs uniques.

Irrélevance

Comme indiqué dans l'introduction, il existe toujours au moins un petit écart entre les données et la réalité. Un professionnel du ML avisé doit déterminer si l'ensemble de données est pertinent pour la question posée.

Huff décrit une première étude d'opinion publique qui a révélé que les réponses des Américains blancs à la question de la facilité avec laquelle les Américains noirs peuvent gagner un bon salaire étaient directement et inversement liées à leur niveau de sympathie envers les Américains noirs. À mesure que l'animosité raciale augmentait, les réponses concernant les opportunités économiques attendues devenaient de plus en plus optimistes. Cela aurait pu être interprété comme un signe de progrès. Cependant, l'étude ne pouvait rien montrer sur les opportunités économiques réelles disponibles pour les Américains noirs à l'époque et n'était pas adaptée pour tirer des conclusions sur la réalité du marché du travail, mais uniquement sur les opinions des personnes interrogées. Les données collectées n'étaient en fait pas pertinentes pour l'état du marché du travail.²

Vous pouvez entraîner un modèle sur des données d'enquête comme celles décrites ci-dessus, où la sortie mesure en réalité l'optimisme plutôt que l'opportunité. Toutefois, comme les opportunités prédites ne sont pas pertinentes pour les opportunités réelles, si vous prétendez que le modèle prédit des opportunités réelles, vous donneriez une fausse représentation de ce qu'il prédit.

Confondus

Une variable de confusion, un facteur de confusion ou un covariateur est une variable qui n'est pas étudiée,mais qui influence les variables étudiées et peut fausser les résultats. Prenons l'exemple d'un modèle de ML qui prédit les taux de mortalité d'un pays en fonction des caractéristiques des politiques de santé publique. Supposons que l'âge médian ne soit pas une caractéristique. Supposons également que certains pays ont une population plus âgée que d'autres. En ignorant la variable de confusion de l'âge médian, ce modèle pourrait prédire des taux de mortalité incorrects.

Aux États-Unis, l'appartenance ethnique est souvent fortement corrélée à la classe socio-économique, mais seule l'appartenance ethnique, et non la classe, est enregistrée avec les données de mortalité. Les facteurs de confusion liés à la classe sociale, comme l'accès aux soins de santé, la nutrition, le travail dangereux et le logement sécurisé, peuvent avoir une influence plus forte sur les taux de mortalité que la race, mais être négligés, car ils ne sont pas inclus dans les ensembles de données³.L'identification et le contrôle de ces facteurs de confusion sont essentiels pour créer des modèles utiles et tirer des conclusions pertinentes et précises.

Si un modèle est entraîné sur des données de mortalité existantes, qui incluent la race, mais pas la classe, il peut prédire la mortalité en fonction de la race, même si la classe est un prédicteur plus fort de la mortalité. Cela pourrait entraîner des hypothèses inexactes sur la causalité et des prédictions inexactes sur la mortalité des patients. Les professionnels du ML doivent se demander si des variables parasites existent dans leurs données, ainsi que quelles variables significatives pourraient être manquantes dans leur ensemble de données.

En 1985, l'étude Nurses' Health Study, une étude de cohorte observationnelle de la Harvard Medical School et de la Harvard School of Public Health, a révélé que les membres de la cohorte sous traitement hormonal de substitution avaient une incidence de crise cardiaque plus faible que les membres de la cohorte qui n'avaient jamais pris d'œstrogène. Par conséquent, les médecins ont prescrit de l'œstrogène à leurs patientes ménopausées et postménopausées pendant des décennies, jusqu'à ce qu'une étude clinique en 2002 identifie les risques pour la santé créés par la thérapie œstrogénique à long terme. La pratique de la prescription d'œstrogène aux femmes postménopausées a été arrêtée, mais pas avant d'avoir causé des dizaines de milliers de décès prématurés.

Plusieurs facteurs de confusion peuvent avoir causé cette association. Les épidémiologistes ont constaté que les femmes qui suivent une thérapie hormonale de remplacement, par rapport aux femmes qui ne le font pas, ont tendance à être plus minces, plus instruites, plus riches, plus conscientes de leur santé et plus susceptibles de faire de l'exercice. Dans différentes études, l'éducation et la richesse ont été associées à une réduction du risque de maladie cardiaque. Ces effets auraient brouillé la corrélation apparente entre la thérapie œstrogénique et les crises cardiaques⁴.

Pourcentages avec des nombres négatifs

Évitez d'utiliser des pourcentages lorsque des nombres négatifs sont présents⁵,car tous les types de gains et de pertes significatifs peuvent être masqués. Pour simplifier les calculs, supposons que le secteur de la restauration emploie deux millions de personnes. Si le secteur perd un million de ces emplois fin mars 2020, ne connaît aucun changement net pendant dix mois et retrouve 900 000 emplois début février 2021, une comparaison annuelle début mars 2021 ne suggérerait qu'une perte de 5% des emplois dans les restaurants. En supposant qu'il n'y ait pas d'autres changements, une comparaison annuelle à la fin du mois d'avril 2021 suggèrerait une augmentation de 90% des emplois dans les restaurants, ce qui est très différent de la réalité.

Privilégiez les chiffres réels, normalisés si nécessaire. Pour en savoir plus, consultez Utiliser des données numériques.

Biais post-hoc et corrélations inutilisables

La faute de raisonnement post-hoc consiste à supposer que, parce que l'événement A a été suivi de l'événement B, l'événement A a causé l'événement B. En d'autres termes, il s'agit d'une relation de cause à effet qui n'existe pas. Plus simplement : les corrélations ne prouvent pas de causalité.

En plus d'une relation de cause à effet claire, les corrélations peuvent également découler des éléments suivants:

• Pure coïncidence (voir les corrélations factices de Tyler Vigen pour des illustrations, y compris une forte corrélation entre le taux de divorce dans le Maine et la consommation de margarine).
• Relation réelle entre deux variables, même si la variable causale et celle affectée restent indéterminées.
• Une troisième cause distincte qui influence les deux variables, même si les variables corrélées ne sont pas liées entre elles. Par exemple, l'inflation mondiale peut faire augmenter les prix des yachts et du céleri.⁶

Il est également risqué d'extrapoler une corrélation au-delà des données existantes. Huff souligne que la pluie peut améliorer les récoltes, mais qu'une trop grande quantité de pluie peut les endommager.La relation entre la pluie et les résultats des récoltes est non linéaire⁷ (voir les deux sections suivantes pour en savoir plus sur les relations non linéaires). Jones note que le monde est rempli d'événements imprévisibles, comme la guerre et la famine, qui soumettent les futures prévisions des données de séries temporelles à une énorme incertitude.⁸

De plus, même une corrélation authentique basée sur la cause à effet peut ne pas être utile pour prendre des décisions. Huff donne, à titre d'exemple, la corrélation entre l'aptitude au mariage et l'enseignement supérieur dans les années 1950. Les femmes qui ont fait des études supérieures étaient moins susceptibles de se marier, mais il se peut qu'elles aient été moins enclines à se marier dès le départ. Si tel était le cas, un diplôme universitaire ne changeait pas la probabilité de se marier.⁹

Si une analyse détecte une corrélation entre deux variables d'un ensemble de données, posez-vous les questions suivantes:

• De quel type de corrélation s'agit-il: relation de cause à effet, relation factice, relation inconnue ou causée par une troisième variable ?
• Quelle est la fiabilité de l'extrapolation à partir des données ? Chaque prédiction de modèle sur des données qui ne figurent pas dans l'ensemble de données d'entraînement est, en fait, une interpolation ou une extrapolation à partir des données.
• La corrélation peut-elle être utilisée pour prendre des décisions utiles ? Par exemple, l'optimisme peut être fortement corrélé à l'augmentation des salaires, mais l'analyse du sentiment d'un grand corpus de données textuelles, telles que les posts sur les réseaux sociaux des utilisateurs d'un pays donné, ne serait pas utile pour prédire l'augmentation des salaires dans ce pays.

Lors de l'entraînement d'un modèle, les professionnels du ML recherchent généralement des caractéristiques fortement corrélées au libellé. Si la relation entre les caractéristiques et l'étiquette n'est pas bien comprise, cela peut entraîner les problèmes décrits dans cette section, y compris les modèles basés sur des corrélations factices et les modèles qui supposent que les tendances historiques se poursuivront à l'avenir, alors qu'en réalité, ce n'est pas le cas.

Le biais linéaire

Dans "Linear Thinking in a Nonlinear World" (Pensée linéaire dans un monde non linéaire), Bart de Langhe, Stefano Puntoni et Richard Larrick décrivent le biais linéaire comme la tendance du cerveau humain à s'attendre à des relations linéaires et à les rechercher, bien que de nombreux phénomènes soient non linéaires. La relation entre les attitudes et le comportement humains, par exemple, est une courbe convexe et non une ligne. Dans un article publié dans le Journal of Consumer Policy en 2007, cité par de Langhe et al., Jenny van Doorn et al. ont modélisé la relation entre l'intérêt des personnes interrogées pour l'environnement et leurs achats de produits biologiques. Les personnes les plus préoccupées par l'environnement ont acheté plus de produits bio, mais il y avait très peu de différence entre tous les autres répondants.

Graphique des achats bio par rapport au score d'intérêt environnemental simplifié et adapté de l'article de van Doorn et al.

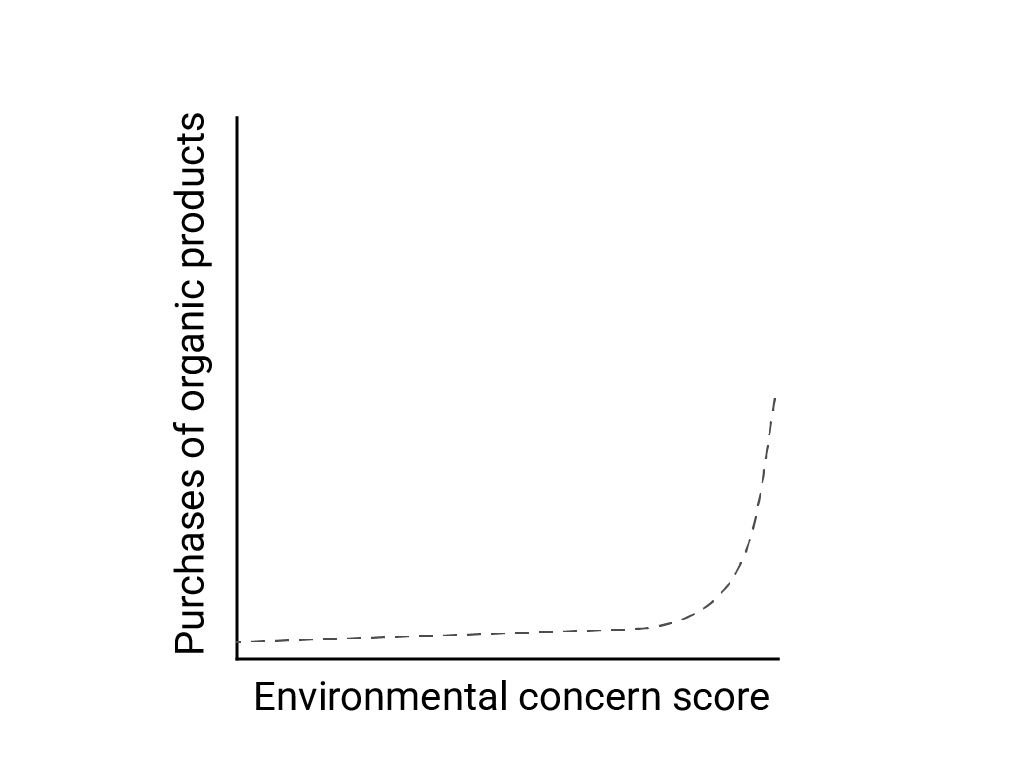
Lorsque vous concevez des modèles ou des études, tenez compte de la possibilité de relations non linéaires. Étant donné que les tests A/B peuvent passer à côté de relations non linéaires, envisagez également de tester une troisième condition intermédiaire, C. Demandez-vous également si le comportement initial qui semble linéaire continuera de l'être, ou si les données futures pourraient présenter un comportement plus logarithmique ou autre non linéaire.

Exemple d'ajustement linéaire médiocre aux données logarithmiques

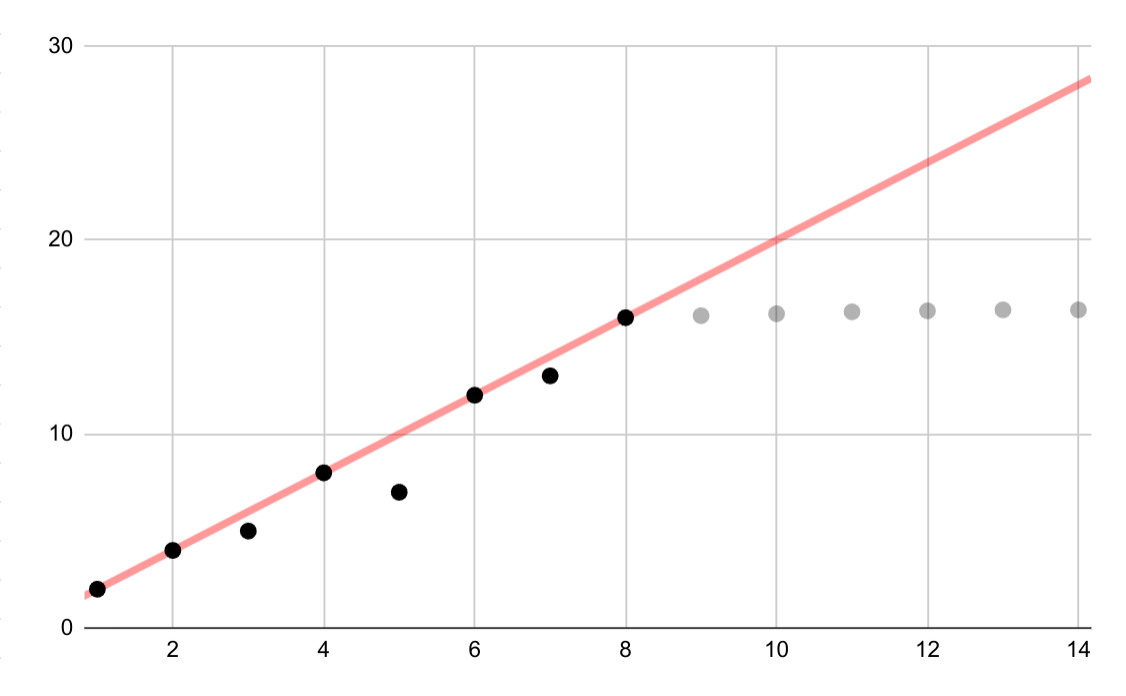
Cet exemple hypothétique montre une adéquation linéaire erronée pour des données logarithmiques. Si seuls les premiers points de données étaient disponibles, il serait tentant, mais incorrect, de supposer une relation linéaire continue entre les variables.

Interpolation linéaire

Examinez toute interpolation entre les points de données, car l'interpolation introduit des points fictifs, et les intervalles entre les mesures réelles peuvent contenir des fluctuations significatives. Prenons l'exemple de la visualisation suivante de quatre points de données connectés par des interpolations linéaires:

Exemple d'interpolation linéaire.

Considérons ensuite cet exemple de fluctuations entre les points de données effacés par une interpolation linéaire:

Exemple de fluctuation significative (un tremblement de terre) entre les points de données.

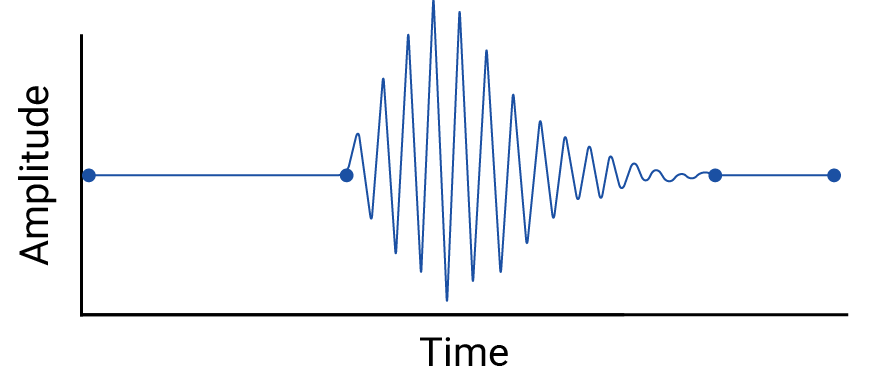
Cet exemple est artificiel, car les sismographes collectent des données continues et ne manqueraient donc pas ce tremblement de terre. Cependant, il est utile pour illustrer les hypothèses faites par les interpolations et les phénomènes réels que les professionnels des données pourraient manquer.

Phénomène de Runge

Le phénomène de Runge, également appelé "oscillation polynomiale", est un problème situé à l'extrémité opposée du spectre de l'interpolation linéaire et du biais linéaire. Lorsque vous ajustez une interpolation polynomiale aux données, il est possible d'utiliser un polynôme de degré trop élevé (le degré, ou l'ordre, étant l'exposant le plus élevé de l'équation polynomiale). Cela produit des oscillations étranges sur les bords. Par exemple, appliquer une interpolation polynomiale de degré 11, ce qui signifie que le terme de plus haut degré de l'équation polynomiale a \(x^{11}\), à des données approximativement linéaires, donne des prédictions remarquablement mauvaises au début et à la fin de la plage de données:

Exemple de mouvement polynomial

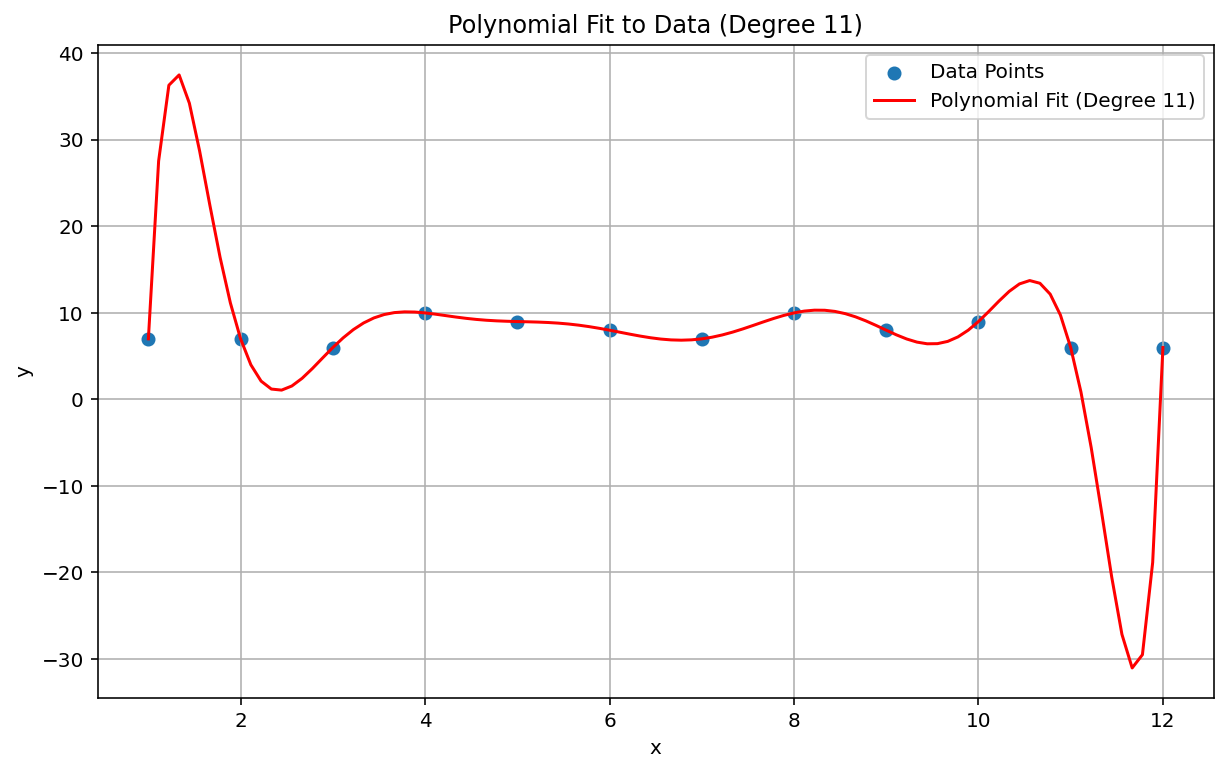
Dans le contexte du ML, un phénomène analogue est l'overfitting.

Échecs de détection statistique

Il arrive qu'un test statistique soit trop faible pour détecter un petit effet. Une faible puissance dans l'analyse statistique signifie que les chances d'identifier correctement les événements réels sont faibles, ce qui entraîne un risque élevé de faux négatifs. Dans Nature, Katherine Button et al. ont écrit: "Lorsque des études dans un domaine donné sont conçues avec une puissance de 20%, cela signifie que s'il existe 100 effets non nuls authentiques à découvrir dans ce domaine, ces études ne devraient en découvrir que 20." Augmenter la taille de l'échantillon peut parfois être utile, tout comme une conception d'étude minutieuse.

Une situation analogue en ML est le problème de classification et le choix d'un seuil de classification. Un seuil plus élevé entraîne moins de faux positifs et plus de faux négatifs, tandis qu'un seuil plus bas entraîne plus de faux positifs et moins de faux négatifs.

En plus des problèmes liés à la puissance statistique, étant donné que la corrélation est conçue pour détecter des relations linéaires, les corrélations non linéaires entre les variables peuvent être manquées. De même, les variables peuvent être liées les unes aux autres, mais ne pas être corrélées statistiquement. Les variables peuvent également être corrélées négativement, mais complètement indépendantes, ce qui est appelé le paradoxe de Berkson ou l'erreur de Berkson. L'exemple classique de l'erreur de Berkson est la corrélation négative factice entre un facteur de risque et une maladie grave lorsque l'on examine une population d'hospitalisation (par rapport à la population générale), qui découle du processus de sélection (une maladie suffisamment grave pour nécessiter une hospitalisation).

Vérifiez si l'une de ces situations s'applique à vous.

Modèles obsolètes et hypothèses non valides

Même de bons modèles peuvent se dégrader au fil du temps, car le comportement (et le monde, d'ailleurs) peut changer. Les premiers modèles prédictifs de Netflix ont dû être abandonnés, car leur base de clients est passée de jeunes utilisateurs avertis de la technologie à la population générale¹⁰.

Les modèles peuvent également contenir des hypothèses silencieuses et inexactes qui peuvent rester cachées jusqu'à l'échec catastrophique du modèle, comme lors du krach boursier de 2008. Les modèles de valeur à risque (VaR) de l'industrie financière prétendaient estimer précisément la perte maximale sur le portefeuille de n'importe quel trader, par exemple une perte maximale de 100 000$ attendue dans 99% des cas. Toutefois, dans les conditions anormales du krach, un portefeuille dont la perte maximale attendue était de 100 000$ perdait parfois 1 000 000$ ou plus.

Les modèles VaR étaient basés sur des hypothèses erronées, y compris les suivantes:

• Les fluctuations passées du marché permettent de prévoir les fluctuations futures.
• Une distribution normale (à queue fine et donc prévisible) sous-tendait les rendements prévus.

Graphique de la distribution de von Mises, qui présente des queues fines à K élevé et des queues épaisses à K faible.

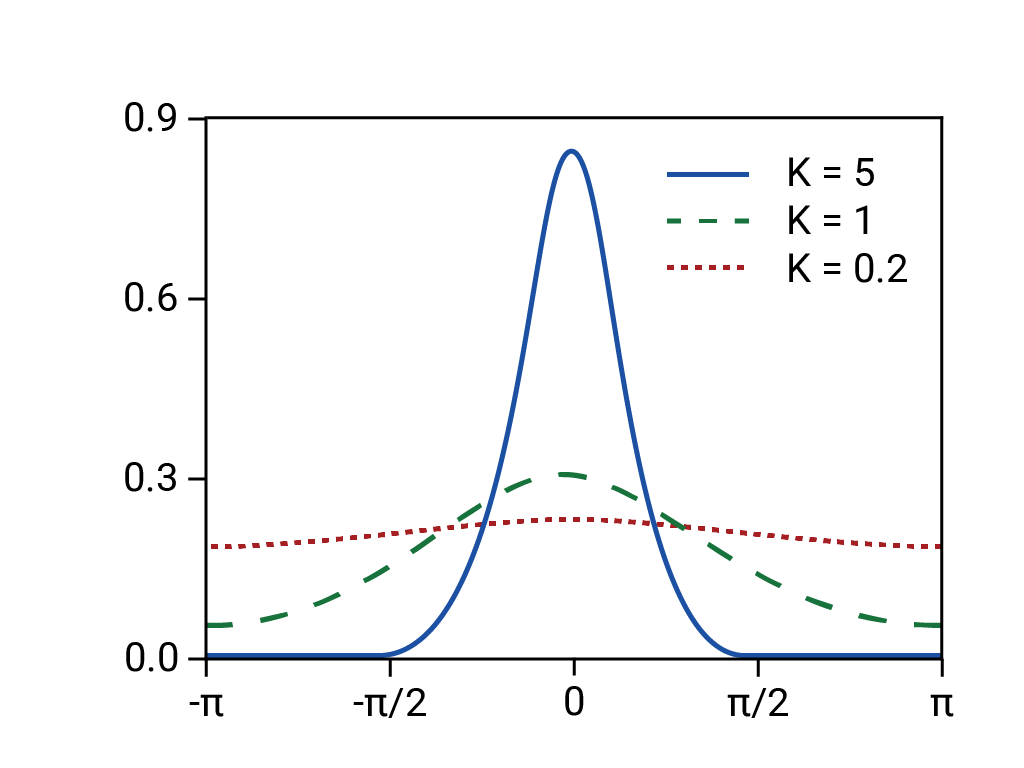
En réalité, la distribution sous-jacente était à queue épaisse, "sauvage" ou fractale, ce qui signifie qu'il y avait un risque beaucoup plus élevé d'événements à queue longue, extrêmes et supposément rares qu'une distribution normale ne le prévoyait. La nature à queue épaisse de la distribution réelle était bien connue, mais aucune mesure n'a été prise. Ce qui était moins connu était la complexité et l'imbrication étroite de divers phénomènes, y compris les transactions informatisées avec des ventes automatiques.¹¹

Problèmes d'agrégation

Les données agrégées, qui incluent la plupart des données démographiques et épidémiologiques, sont soumises à un ensemble particulier de pièges. Le paradoxe de Simpson, ou paradoxe de l'agrégation, se produit dans les données agrégées où les tendances apparentes disparaissent ou s'inversent lorsque les données sont agrégées à un niveau différent, en raison de facteurs de confusion et de relations causales mal comprises.

Le paralogisme écologique consiste à extrapoler de manière erronée des informations sur une population à un niveau d'agrégation à un autre niveau d'agrégation, où l'affirmation peut ne pas être valide. Une maladie qui touche 40% des travailleurs agricoles d'une province peut ne pas être présente avec la même prévalence dans la population générale. Il est également très probable que des fermes isolées ou des villes agricoles de cette province ne souffrent pas d'une prévalence aussi élevée de cette maladie. Il serait fallacieux de supposer une prévalence de 40% dans ces régions moins touchées.

Le problème des unités spatiales modifiables (MAUP, modifiable areal unit problem) est un problème bien connu des données géospatiales, décrit par Stan Openshaw en 1984 dans CATMOG 38. En fonction des formes et des tailles des zones utilisées pour agréger les données, un spécialiste des données géospatiales peut établir presque toutes les corrélations entre les variables des données. Le dessin de circonscriptions électorales qui favorisent un parti ou un autre est un exemple de MAUP.

Toutes ces situations impliquent une extrapolation inappropriée d'un niveau d'agrégation à un autre. Différents niveaux d'analyse peuvent nécessiter différentes agrégations, voire des ensembles de données entièrement différents.¹²

Notez que les données du recensement, démographiques et épidémiologiques sont généralement agrégées par zones pour des raisons de confidentialité. Ces zones sont souvent arbitraires, c'est-à-dire qu'elles ne sont pas basées sur des limites réelles significatives. Lorsque vous travaillez avec ces types de données, les professionnels du ML doivent vérifier si les performances et les prédictions du modèle changent en fonction de la taille et de la forme des zones sélectionnées ou du niveau d'agrégation, et si oui, si les prédictions du modèle sont affectées par l'un de ces problèmes d'agrégation.

Références

Button, Katharine et al. "Power failure: why small sample size undermines the reliability of neuroscience." Nature Reviews Neuroscience, vol. 14 (2013), 365-376. DOI : https://doi.org/10.1038/nrn3475

Cairo, Alberto. How Charts Lie: Getting Smarter about Visual Information NY : W.W. Norton, 2019.

Davenport, Thomas H. "A Predictive Analytics Primer" (Présentation de l'analyse prédictive). Dans le Guide HBR sur les principes de base de l'analyse de données pour les responsables (Boston: HBR Press, 2018), p. 81-86.

De Langhe, Bart, Stefano Puntoni et Richard Larrick. "Linear Thinking in a Nonlinear World" (Pensée linéaire dans un monde non linéaire). Dans le Guide HBR sur les bases de l'analyse de données pour les responsables (Boston, HBR Press, 2018), p. 131-154.

Ellenberg, Jordan. How Not to Be Wrong: The Power of Mathematical Thinking New York: Penguin, 2014.

Huff, Darrell. How to Lie with Statistics. NY: W.W. Norton, 1954.

Jones, Ben. Éviter les pièges liés aux données Hoboken, NJ: Wiley, 2020.

Openshaw, Stan. "The Modifiable Areal Unit Problem", CATMOG 38 (Norwich, Angleterre: Geo Books, 1984), p. 37.

The Risks of Financial Modeling: VaR and the Economic Meltdown, 111e Congrès (2009) (témoignages de Nassim N. Taleb et Richard Bookstaber).

Ritter, David. "When to Act on a Correlation, and When Not To" (Quand agir en fonction d'une corrélation et quand ne pas le faire) Dans le Guide HBR sur les principes de base de l'analyse de données pour les responsables (Boston, HBR Press, 2018), p. 103-109.

Tulchinsky, Theodore H. et Elena A. Varavikova. "Chapter 3: Measuring, Monitoring, and Evaluating the Health of a Population" in The New Public Health, 3rd ed. San Diego: Academic Press, 2014, pp 91-147. DOI: https://doi.org/10.1016/B978-0-12-415766-8.00003-3.

Van Doorn, Jenny, Peter C. Verhoef, et Tammo H. A. Bijmolt. "Importance des relations non linéaires entre l'attitude et le comportement dans la recherche sur les politiques." Journal of Consumer Policy 30 (2007) 75-90. DOI: https://doi.org/10.1007/s10603-007-9028-3

Image de référence

Basé sur la "distribution de Von Mises". Rainald62, 2018. Source

---

1. Ellenberg 125. ↩

2. Huff 77-79. Huff cite le Bureau de recherche sur l'opinion publique de Princeton, mais il a peut-être pensé au rapport d'avril 1944 du National Opinion Research Center de l'université de Denver. ↩

3. Tulchinsky et Varavikova. ↩

4. Gary Taubes, Do We Really Know What Makes Us Healthy?" (Savons-nous vraiment ce qui nous rend en bonne santé ?) dans The New York Times Magazine, 16 septembre 2007. ↩

5. Ellenberg 78. ↩

6. Huff 91-92. ↩

7. Huff 93. ↩

8. Jones 157-167. ↩

9. Huff 95. ↩

10. Davenport 84. ↩

11. Voir le témoignage de Nassim N. devant le Congrès Taleb et Richard Bookstaber dans The Risks of Financial Modeling: VaR and the Economic Meltdown, 111th Congress (2009) 11-67. ↩

12. Le Caire 155, 162. ↩