分析トラップ

「すべてのモデルは間違っているが、中には役に立つものもある」- George Box、1978 年

統計手法は強力ですが、制限もあります。これらの制限を理解することで、シェイクスピアが偶然が予測する以上の頭韻を踏んでいないという BF スキナーの主張など、研究者が不用意な発言や不正確な主張を回避できます。（スキナーの研究は統計的に不十分でした¹）。

不確実性と誤差棒

分析では不確実性を指定することが重要です。他の人の分析における不確実性を定量化することも同様に重要です。グラフにトレンドをプロットしているように見えるデータポイントでも、誤差バーが重なっている場合は、パターンがまったく示されていない可能性があります。また、特定の調査や統計テストから有用な結論を導き出すには、不確実性が高すぎる場合もあります。研究調査で区画レベルの精度が必要な場合、不確実性が ±500 m の地理空間データセットは、不確実性が高すぎて使用できません。

また、不確実性のレベルは意思決定プロセスで役立つ場合があります。特定の水処理を裏付けるデータで、結果に 20% の不確実性がある場合、その水処理を実装し、その不確実性に対処するためにプログラムの継続的なモニタリングを行うことが推奨される場合があります。

ベイズ ニューラル ネットワークは、単一の値ではなく値の分布を予測することで、不確実性を定量化できます。

無関係

冒頭で説明したように、データと現実の間には常に少なくとも小さなギャップがあります。賢明な ML 実務者は、データセットが質問に関連しているかどうかを判断する必要があります。

ハフは、アフリカ系アメリカ人が豊かな生活を送るのはどのくらい簡単かという質問に対する白人アメリカ人の回答が、アフリカ系アメリカ人に対する共感のレベルと直接的かつ逆に関連していることを示す初期の世論調査について説明しています。人種的な敵意が高まるにつれ、期待される経済的機会に関する回答はますます楽観的になりました。これは、進展の兆候と誤解された可能性があります。しかし、この調査では、当時の黒人アメリカ人が利用できる実際の経済的機会について何も示すことができず、調査回答者の意見のみを基に、雇用市場の現実について結論を導き出すには適していませんでした。収集されたデータは、実際には労働市場の状況とは無関係でした。²

上記のようなアンケートデータでモデルをトレーニングできます。この場合、出力は「機会」ではなく「楽観主義」を測定します。ただし、予測された商談は実際の商談とは無関係であるため、モデルが実際の商談を予測していると主張すると、モデルが予測するものを誤って表現していることになります。

交絡

交絡変数、交絡、共変量とは、調査対象ではない変数で、調査対象の変数に影響し、結果を歪める可能性がある変数です。たとえば、公衆衛生政策の特徴に基づいて入力国の死亡率を予測する ML モデルについて考えてみましょう。平均年齢が特徴量ではないとします。さらに、一部の国では人口の高齢化が進んでいるとします。このモデルでは、中央値年齢という混同変数を無視しているため、死亡率が誤って予測される可能性があります。

米国では、人種は社会経済的階層と強く相関していますが、死亡データには階層ではなく人種のみが記録されます。医療へのアクセス、栄養、危険な労働、安全な住宅など、階級に関連する混同要因は、人種よりも死亡率に強い影響を与える可能性があります。しかし、データセットに含まれていないため、無視されがちです。³ 有用なモデルを構築し、有意で正確な結論を導くには、こうした混同要因を特定してコントロールすることが重要です。

既存の死亡率データ（人種は含まれるが階級は含まれない）でモデルをトレーニングした場合、階級が死亡率のより強力な予測因子であっても、人種に基づいて死亡率を予測する可能性があります。これにより、因果関係に関する不正確な前提や、患者の死亡率に関する不正確な予測につながる可能性があります。ML 担当者は、データに混同が存在するかどうか、またデータセットから欠落している有意な変数があるかどうかを尋ねる必要があります。

1985 年にハーバード医学大学院とハーバード公衆衛生大学院が実施した看護師健康調査（観察コホート調査）では、エストロゲン補充療法を受けているコホート メンバーは、エストロゲンを服用したことがないコホート メンバーと比較して心臓発作の発生率が低いことがわかりました。その結果、医師は数十年にわたって、更年期や閉経後の患者にエストロゲンを処方していましたが、2002 年の臨床研究で、長期間のエストロゲン療法による健康上のリスクが特定されました。閉経後の女性にエストロゲンを処方する慣行は停止されましたが、推定で数万人の早期死亡を引き起こす前に停止されました。

複数の混同要因が関連付けの原因となっている可能性があります。疫学者は、ホルモン補充療法を受けている女性は、受けていない女性と比較して、体重が軽く、教育水準が高く、裕福で、健康に気を配り、運動する傾向があることを発見しました。さまざまな研究で、教育と富が心臓病のリスクを軽減することが示されています。これらの効果は、エストロゲン療法と心臓発作の明らかな相関関係を混同させる可能性があります。⁴

負の数値を含む割合

負の値が含まれている場合は、パーセンテージを使用しないでください。⁵ 有意な損益がわかりにくくなる可能性があります。簡単な計算のために、レストラン業界には 200 万人の雇用があると仮定します。2020 年 3 月下旬に 100 万人の雇用が失われ、10 か月間変化がなく、2021 年 2 月上旬に 90 万人の雇用が回復した場合、2021 年 3 月上旬のレストランの雇用は前年比で 5% しか減少していません。他に変化がないとして、2021 年 4 月末の年率比較では、レストランの求人が 90% 増加したことを示唆していますが、これは現実とは大きく異なります。

適切に正規化された実際の数値を優先します。詳細については、数値データの操作をご覧ください。

後付けの誤謬と使用できない相関

後因推論の誤謬とは、イベント A の後にイベント B が発生したため、イベント A がイベント B の原因であると仮定することです。簡単に言えば、因果関係が存在しない場合に因果関係があると仮定することです。もっと簡単に言えば、相関関係は因果関係を証明するものではありません。

明確な因果関係に加えて、相関は次のような要因からも生じる可能性があります。

• 偶然（メイン州の離婚率とマーガリンの消費量の強い相関関係など、Tyler Vigen の虚偽の相関関係を参照）。
• 2 つの変数間の実際の関係。ただし、どの変数が原因で、どの変数が影響を受けているのかは不明です。
• 相関関係にある変数は互いに無関係ですが、両方の変数に影響する 3 つ目の別個の原因。たとえば、世界的なインフレによって、ヨットとセロリの両方の価格が上昇する可能性があります。⁶

また、既存のデータを超えて相関関係を推定するのもリスクがあります。ハフは、雨が降ると作物は成長しますが、雨が多すぎると作物に損傷を与え、雨と作物の収穫量の関係は非線形であると指摘しています。⁷（非線形の関係の詳細については、次の 2 つのセクションをご覧ください）。ジョーンズは、世界には戦争や飢饉など、予測不可能な出来事が多く、時系列データの将来の予測には膨大な不確実性が伴うと指摘しています。⁸

さらに、因果関係に基づく真の相関であっても、意思決定に役立たない場合があります。ハフは、1950 年代の結婚適齢と大学教育の相関関係を例に挙げています。大学に通った女性は結婚する可能性が低かったが、そもそも大学に通った女性は結婚する意向が薄かった可能性もあります。その場合、大学教育を受けていても、結婚する可能性は変わりませんでした。⁹

分析でデータセット内の 2 つの変数の間に相関が検出された場合は、次のように尋ねます。

• どのような相関関係ですか？因果関係、虚偽の関係、不明な関係、第 3 変数によって引き起こされる関係のどれですか？
• データから外挿することにはどの程度のリスクがありますか？トレーニング データセットにないデータに対するすべてのモデル予測は、実際にはデータからの補間または外挿です。
• この相関関係は、有用な意思決定に使用できますか？たとえば、楽観主義は賃金の増加と強く相関している可能性がありますが、特定の国でのユーザーによるソーシャル メディア投稿など、大規模なテキストデータ コーパスの感情分析は、その国の賃金の増加を予測するのに役立ちません。

モデルをトレーニングする際、ML 担当者は通常、ラベルと強く相関する特徴を探します。特徴とラベルの関係が十分に理解されていないと、このセクションで説明する問題が発生する可能性があります。たとえば、虚偽の相関関係に基づくモデルや、過去の傾向が将来も続くと想定しているモデル（実際にはそうではない）などです。

線形バイアス

「非線形の世界における線形思考」で、Bart de Langhe、Stefano Puntoni、Richard Larrick は、多くの現象が非線形であるにもかかわらず、線形の関係を予測して探す人間の脳の傾向を線形バイアスと表現しています。たとえば、人間の態度と行動の関係は、線ではなく凸曲線です。de Langhe らによって引用された 2007 年の Journal of Consumer Policy の論文では、Jenny van Doorn らは、アンケート回答者の環境に対する懸念と、回答者のオーガニック製品の購入の関係をモデル化しました。環境に対する懸念が最も強い人はオーガニック製品をより多く購入していましたが、他の回答者間ではほとんど差異はありませんでした。

van Doorn らによる論文を基に簡素化、改変した、オーガニック食品の購入と環境への懸念スコアのグラフ

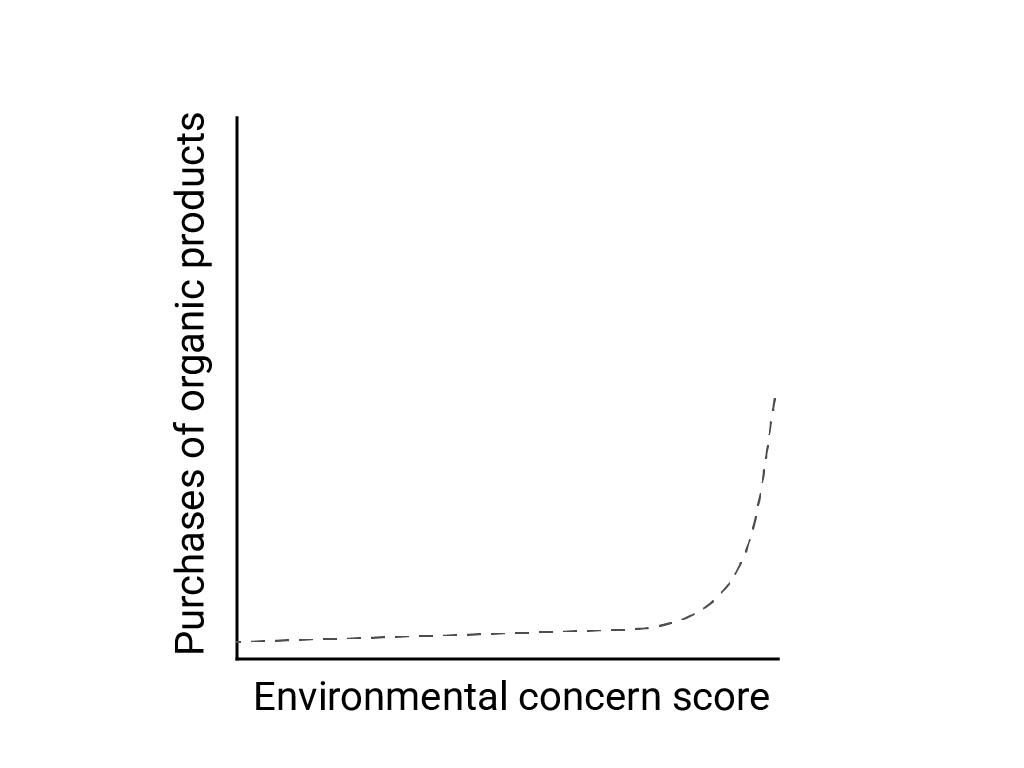
モデルや調査を設計する際は、非線形の関係の可能性を考慮してください。A/B テストでは非線形の関係を見逃す可能性があるため、3 つ目の中間条件 C もテストすることを検討してください。また、線形に見える初期動作が引き続き線形であるかどうか、将来のデータで対数的またはその他の非線形動作が示されるかどうかも考慮してください。

対数データに適さない線形近似の例

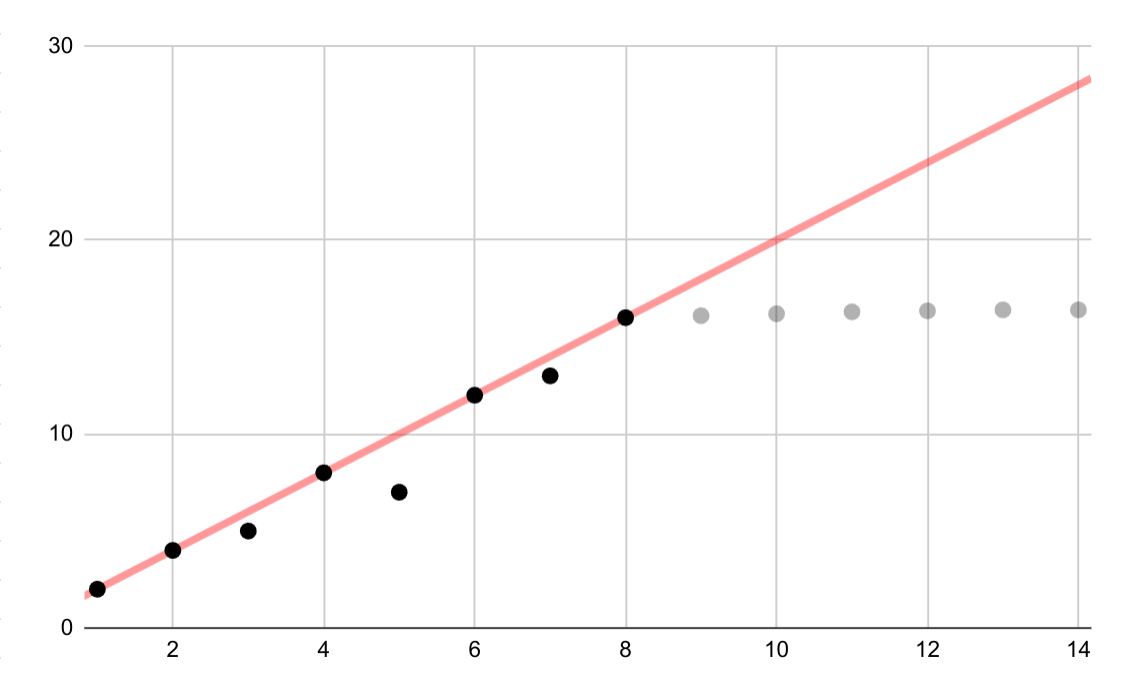
この架空の例は、対数データに対する誤った線形近似を示しています。最初の数個のデータポイントしか利用できない場合は、変数間に継続的な線形関係があると想定するのは魅力的ですが、誤りです。

線形補間

補間では架空のポイントが導入され、実際の測定値の間隔に有意な変動が生じる可能性があるため、データポイント間の補間を確認します。たとえば、線形補間によって接続された 4 つのデータポイントの次のビジュアリゼーションについて考えてみましょう。

線形補間の例。

次に、線形補間によって消去されるデータポイント間の変動の例について考えてみましょう。

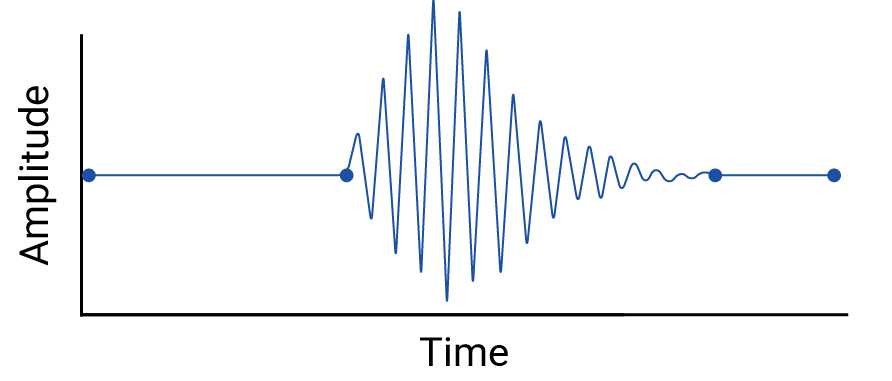データポイント間の有意な変動（地震）の例。

この例は不自然です。なぜなら、地震計は継続的にデータを収集するため、この地震は記録に残ります。ただし、補間によって行われた仮定と、データ プロバイダが見逃す可能性のある実際の現象を示すには役立ちます。

Runge 現象

ランゲの現象（「多項式の揺れ」とも呼ばれます）は、線形補間と線形バイアスとは対極の問題です。多項式補間データをフィッティングするときに、高すぎる次数（次数またはオーダーは、多項式方程式の最高指数）の多項式を使用する可能性があります。これにより、エッジで異常な振動が発生します。たとえば、ほぼ線形のデータに 11 次多項式補間（多項式方程式の最高次項に \(x^{11}\)がある）を適用すると、データ範囲の始点と終点で非常に悪い予測結果になります。

多項式の揺れの例

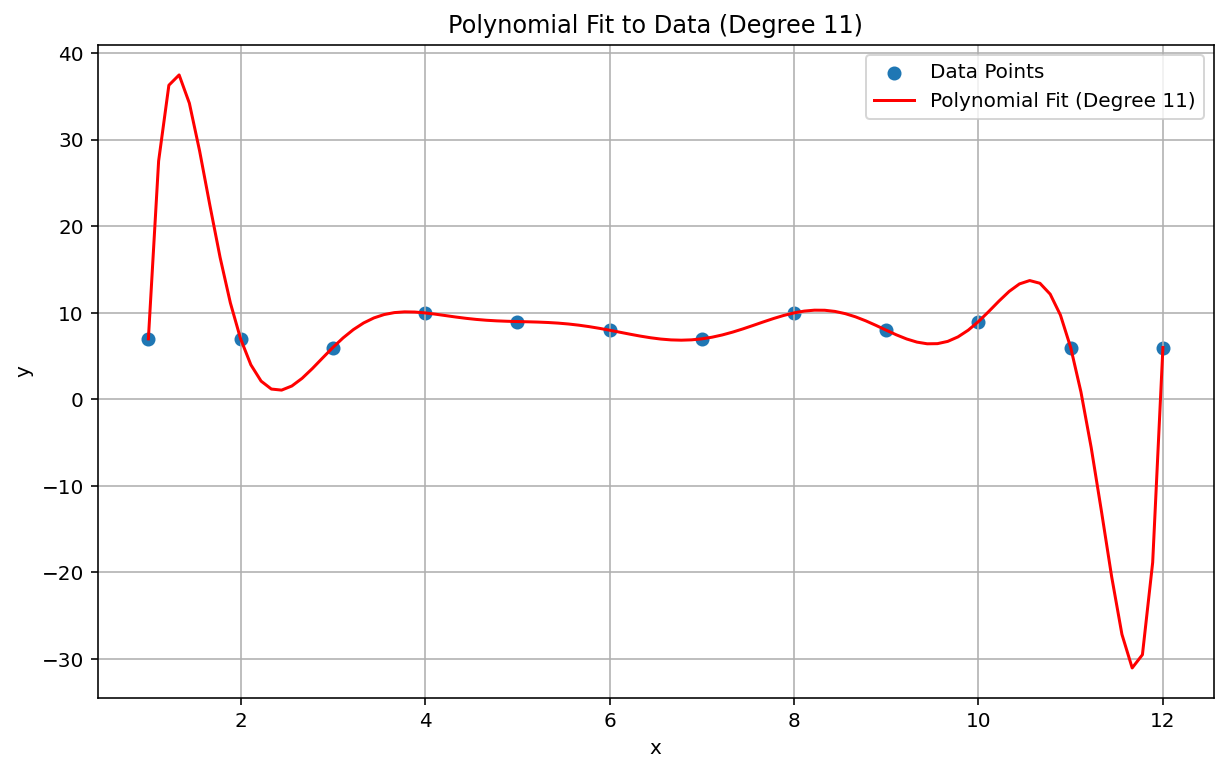
ML のコンテキストでは、同様の現象は過剰適合です。

統計的な検出の失敗

統計テストのパワーが不足して、小さな効果を検出できない場合があります。統計分析の検出力が低いということは、真のイベントを正しく特定する可能性が低く、したがって偽陰性になる可能性が高いことを意味します。Katherine Button らは Nature で次のように述べています。「特定の分野の研究が 20% の検出力で設計されている場合、その分野で検出される真の非ゼロ効果が 100 個ある場合、これらの研究で検出される効果は 20 個のみと予想されます。」サンプルサイズを増やすと、慎重な研究設計と同様に役立つことがあります。

ML における類似の状況は、分類の問題と分類しきい値の選択です。しきい値を高くすると偽陽性は少なくなりますが、偽陰性は多くなります。しきい値を低くすると偽陽性は多くなりますが、偽陰性は少なくなります。

統計的有意性の問題に加えて、相関は線形関係を検出するように設計されているため、変数間の非線形相関が検出されない可能性があります。同様に、変数は相互に関連しているが、統計的に相関していない場合があります。変数は負の相関関係にあるにもかかわらず、まったく関連がないこともあります。これは、バークソンのパラドックスまたはバークソンの誤謬と呼ばれます。バークソンの誤謬の典型的な例は、（一般集団と比較して）病院の入院患者集団を調べた場合に、リスク要因と重症疾患の間に生じる虚偽の負の相関です。これは、選択プロセス（入院を必要とするほど重篤な状態）から生じます。

次のいずれかの状況に当てはまるかどうかを検討します。

古いモデルと無効な前提条件

動作（そして世界）が変化する可能性があるため、優れたモデルでも時間の経過とともに性能が低下する可能性があります。Netflix の初期の予測モデルは、顧客ベースが若いテクノロジーに精通したユーザーから一般ユーザーに変化したため、廃止されました。¹⁰

モデルには、2008 年の市場暴落のように、モデルの致命的な障害が発生するまで隠れたままになる可能性のある、無言で不正確な前提条件が含まれていることもあります。金融業界のバリュー アット リスク（VaR）モデルは、トレーダーのポートフォリオの最大損失を正確に推定すると主張しています。たとえば、99% の確率で最大損失が $100,000 になると予測します。しかし、クラッシュの異常な状況では、最大損失が $100,000 と見込まれるポートフォリオで、$1,000,000 以上の損失が発生することがあります。

VaR モデルは、次のような誤った前提に基づいていました。

• 過去の市場の変化は、将来の市場の変化を予測するうえで役立ちます。
• 予測されたリターンの基盤には、正規分布（薄い尾を持つため予測可能）が存在していた。

K が大きい場合は薄い尾を持ち、K が小さい場合は太い尾を持つフォン ミーゼス分布のグラフ。

実際、基盤となる分布は、長尾分布、または「乱雑な」分布、またはフラクタル分布でした。つまり、正規分布で予測されるよりも、長尾の極端でまれなイベントが発生するリスクがはるかに高かったのです。実際の分布の肥大尾の性質はよく知られていましたが、対応は行われませんでした。あまり知られていないのは、コンピュータベースの取引や自動売却など、さまざまな現象がどれほど複雑で密接に関連しているかということです。¹¹

集計に関する問題

集計されたデータ（ほとんどの人口統計データや疫学データを含む）には、特定の落とし穴があります。シンプソンの逆説（統合の逆説）は、混同要因と因果関係の誤解により、データが別のレベルで集計されたときに、明らかな傾向が消失または逆転する集計データで発生します。

エコロジーの誤謬とは、ある集計レベルの集団に関する情報を、別の集計レベルに誤って外挿することです。この場合、主張が有効でない可能性があります。ある州の農業従事者の 40% が罹患している病気でも、より広範な集団では同じ割合で発生していない可能性があります。また、その州には、その病気の発生率が同程度に高くない孤立した農場や農村がある可能性も非常に高いです。影響の少ない地域でも 40% の有病率があると仮定するのは誤りです。

変更可能な面積単位の問題（MAUP）は、地理空間データでよく知られている問題で、1984 年に Stan Openshaw が CATMOG 38 で説明しています。データの集計に使用されるエリアの形状とサイズに応じて、地理空間データ プロバイダはデータ内の変数間にほぼすべての相関関係を確立できます。特定の政党に有利な選挙区を描画することは、MAUP の例です。

これらの状況はすべて、集計レベル間の不適切な外挿に関連しています。分析レベルが異なると、異なる集計や、まったく異なるデータセットが必要になる場合があります。¹²

なお、国勢調査、人口統計、疫学データは通常、プライバシー上の理由からゾーンごとに集計されます。これらのゾーンは多くの場合、任意のもので、現実世界で意味のある境界に基づいていません。このようなタイプのデータを使用する場合、ML 担当者は、選択したゾーンのサイズと形状、または集計レベルに応じてモデルのパフォーマンスと予測が変化するかどうかを確認し、変化する場合は、モデルの予測がこれらの集計の問題のいずれかに影響されているかどうかを確認する必要があります。

参照

Button, Katharine et al. "Power failure: why small sample size undermines the reliability of neuroscience." Nature Reviews Neuroscience vol 14（2013）、365 ～ 376 ページ。DOI: https://doi.org/10.1038/nrn3475

カイロ、アルベルト様。How Charts Lie: Getting Smarter about Visual InformationNY: W.W. Norton, 2019.

Davenport, Thomas H. 「A Predictive Analytics Primer」HBR Guide to Data Analytics Basics for Managers（ボストン: HBR Press、2018）81 ～ 86 ページ。

De Langhe、Bart、Stefano Puntoni、Richard Larrick 氏。「リニアな世界におけるリニアな思考」HBR Guide to Data Analytics Basics for Managers（ボストン: HBR Press、2018）131 ～ 154 ページ。

Ellenberg、ヨルダン。How Not to Be Wrong: The Power of Mathematical ThinkingNY: Penguin, 2014.

Huff, Darrell. How to Lie with Statistics（統計で嘘をつく方法）NY: W.W. Norton, 1954.

Jones, Ben. データに関する落とし穴を回避するHoboken, NJ: Wiley, 2020.

Openshaw, Stan. 「The Modifiable Areal Unit Problem（変更可能な空間単位の問題）」CATMOG 38（ノリッジ、英国: Geo Books 1984）37 頁。

The Risks of Financial Modeling: VaR and the Economic Meltdown、第 111 回議会（2009 年）（ナシム N. Taleb と Richard Bookstaber による）

Ritter、David「相関関係に基づいて対応すべき場合とそうでない場合」HBR Guide to Data Analytics Basics for Managers（ボストン: HBR Press、2018）103 ～ 109 ページ。

Tulchinsky, Theodore H. and Elena A. Varavikova 氏。「第 3 章: 集団の健康の測定、モニタリング、評価」The New Public Health（第 3 版）サンディエゴ: Academic Press、2014、pp 91-147。DOI: https://doi.org/10.1016/B978-0-12-415766-8.00003-3.

Van Doorn, Jenny, Peter C. Verhoef、Tammo H. A. Bijmolt。「ポリシー調査における態度と行動の非線形関係の重要性」Journal of Consumer Policy 30（2007）75 ～ 90 ページ。DOI: https://doi.org/10.1007/s10603-007-9028-3

画像の参照

「Von Mises Distribution」に基づいています。Rainald62、2018 年。ソース

---

1. Ellenberg 125. ↩

2. Huff 77-79. ハフはプリンストン大学の世論調査室を引用していますが、デンバー大学の国立世論調査センターによる1944 年 4 月の報告を念頭に置いていた可能性があります。 ↩

3. Tulchinsky と Varavikova によるものです。 ↩

4. Gary Taubes、Do We Really Know What Makes Us Healthy?（私たちが健康になる理由を本当に知っていますか？）The New York Times Magazine、2007 年 9 月 16 日。 ↩

5. Ellenberg 78. ↩

6. Huff 91-92. ↩

7. Huff 93。 ↩

8. Jones 157-167。 ↩

9. Huff 95。 ↩

10. Davenport 84. ↩

11. Nassim N. の米国議会での証言をご覧ください。Taleb と Richard Bookstaber の The Risks of Financial Modeling: VaR and the Economic Meltdown、第 111 回議会（2009）11-67。 ↩

12. カイロ 155、162。 ↩