Page Summary
-
Data quality issues such as inaccuracies, errors, and biases can significantly impact the accuracy of machine learning models.
-
Sampling biases like survivorship bias, self-selection bias, and recall bias can skew data and lead to flawed conclusions.
-
Addressing data dirt through cleaning and preprocessing is essential for reliable machine learning outcomes.
-
Small datasets are vulnerable to noise and regression to the mean, requiring careful interpretation of results and consideration of control groups.
-
Clear definitions, unbiased rankings, and an understanding of data collection methods are crucial for accurate analysis in machine learning.
"Garbage in, garbage out."
— Early programming proverb
Beneath every ML model, every calculation of correlation, and every data-based policy recommendation lies one or more raw datasets. No matter how beautiful or striking or persuasive the end products are, if the underlying data was erroneous, badly collected, or low-quality, the resulting model, prediction, visualization, or conclusion will likewise be of low quality. Anyone who visualizes, analyzes, and trains models on datasets should ask hard questions about the source of their data.
Data-collecting instruments can malfunction or be badly calibrated. Data-collecting humans can be tired, mischievous, inconsistent, or poorly trained. People make mistakes, and different people can also reasonably disagree over the classification of ambiguous signals. As a result, the quality and validity of data can suffer, and the data may fail to reflect reality. Ben Jones, author of Avoiding Data Pitfalls, calls this the data-reality gap, reminding the reader: "It's not crime, it's reported crime. It's not the number of meteor strikes, it's the number of recorded meteor strikes."
Examples of the data-reality gap:
Jones graphs spikes in time measurements at 5-minute intervals, and weight measurements at 5-lb intervals, not because such spikes exist in the data, but because human data collectors, unlike instruments, have a tendency to round their numbers to the nearest 0 or 5.1
In 1985, Joe Farman, Brian Gardiner, and Jonathan Shanklin, working for the British Antarctic Survey (BAS), found that their measurements indicated a seasonal hole in the ozone layer over the Southern Hemisphere. This contradicted NASA data, which recorded no such hole. NASA physicist Richard Stolarski investigated and found that NASA's data-processing software was designed under the assumption that ozone levels could never fall below a certain amount, and the very, very low readings of ozone that were detected were automatically tossed out as nonsensical outliers.2
Instruments experience a diversity of failure modes, sometimes while still collecting data. Adam Ringler et al. provide a gallery of seismograph readings resulting from instrument failures (and the corresponding failures) in the 2021 paper "Why Do My Squiggles Look Funny?"3 The activity in the example readouts doesn't correspond to actual seismic activity.
For ML practitioners, it's critical to understand:
- Who collected the data
- How and when the data was collected and under what conditions
- The sensitivity and state of measuring instruments
- What instrument failures and human error might look like in a particular context
- Human tendencies to round numbers and provide desirable answers
Almost always, there's at least a small difference between data and reality, also known as ground truth. Accounting for that difference is key to drawing good conclusions and making sound decisions. This includes deciding:
- which problems can and should be solved by ML.
- which problems are not best solved by ML.
- which problems do not yet have enough high-quality data to be solved by ML.
Ask: What, in the strictest and most literal sense, is communicated by the data? Just as importantly, what isn't communicated by the data?
Dirt in the data
In addition to investigating the conditions of data collection, the dataset itself can contain blunders, errors, and null or invalid values (such as negative measurements of concentration). Crowd-sourced data can be especially messy. Working with a dataset of unknown quality can lead to inaccurate results.
Common issues include:
- Misspellings of string values, like place, species, or brand names
- Incorrect unit conversions, units, or object types
- Missing values
- Consistent misclassifications or mislabeling
- Significant digits left over from mathematical operations that exceed the actual sensitivity of an instrument
Cleaning a dataset often involves choices about null and missing values (whether to keep them as null, drop them, or substitute 0s), correcting spellings to a single version, fixing units and conversions, and so on. A more advanced technique is to impute missing values, which is described in Data characteristics in Machine Learning Crash Course.
Sampling, survivorship bias, and the surrogate endpoint problem
Statistics allows for the valid and accurate extrapolation of results from a purely random sample to the larger population. The unexamined brittleness of this assumption, along with imbalanced and incomplete training inputs, has led to high-profile failures of many ML applications, including models used for resume reviews and policing. It has also led to polling failures and other erroneous conclusions about demographic groups. In most contexts outside of artificial computer-generated data, purely random samples are too expensive and too difficult to acquire. Various workarounds and affordable proxies are used instead, which introduce different sources of bias.
To use the stratified sampling method, for example, you have to know the prevalence of each sampled stratum in the larger population. If you assume a prevalence that is actually incorrect, your results will be inaccurate. Likewise, online polling is rarely a random sample of a national population, but a sample of the internet-connected population (often from multiple countries) that sees and is willing to take the survey. This group is likely to differ from a true random sample. The questions in the poll are a sample of possible questions. Answers to those poll questions are, again, not a random sample of respondents' actual opinions, but a sample of opinions that respondents are comfortable providing, which may differ from their actual opinions.
Clinical health researchers encounter a similar issue known as the surrogate endpoint problem. Because it takes far too long to check a drug's effect on patient lifespan, researchers use proxy biomarkers that are assumed to be related to lifespan but may not be. Cholesterol levels are used as a surrogate endpoint for heart attacks and deaths caused by cardiovascular issues: if a drug reduces cholesterol levels, it's assumed to also lower risk of cardiac issues. However, that chain of correlation may not be valid, or else the order of causation may be other than what the researcher assumes. See Weintraub et al., "The perils of surrogate endpoints", for more examples and details. The equivalent situation in ML is that of proxy labels.
Mathematician Abraham Wald famously identified a data sampling issue now known as survivorship bias. Warplanes were returning with bullet holes in particular locations and not in others. The US military wanted to add more armor to the planes in the areas with the most bullet holes, but Wald's research group recommended instead that the armor be added to areas without bullet holes. They correctly inferred that their data sample was skewed because planes shot in those areas were so badly damaged that they were not able to return to base.
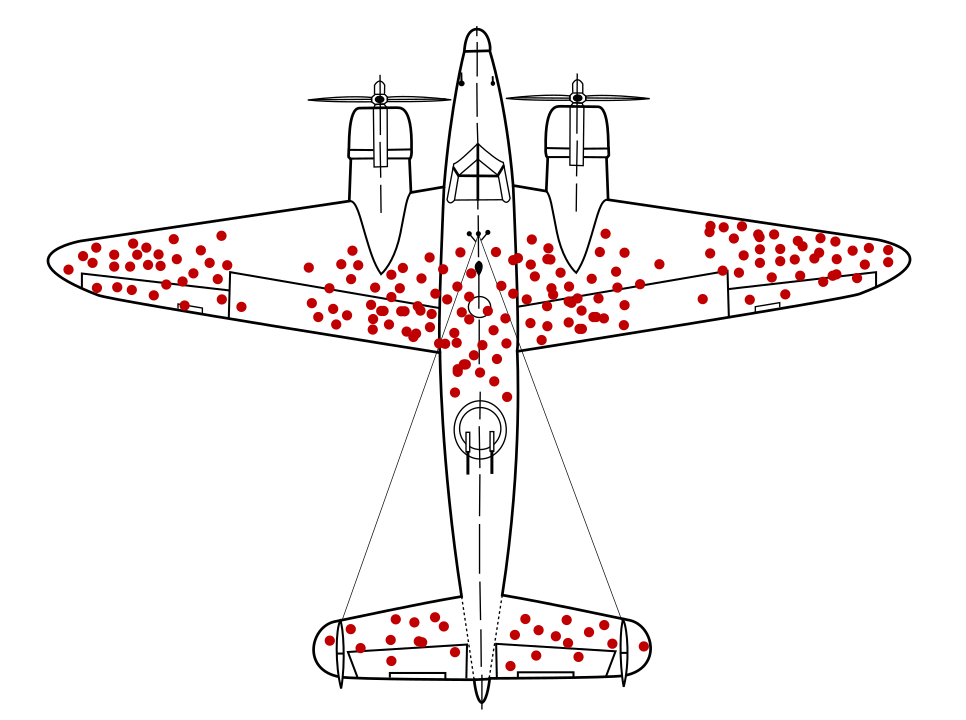
Had an armor-recommending model been trained solely on diagrams of returning warplanes, without insight into the survivorship bias present in the data, that model would have recommended reinforcing the areas with more bullet holes.
Self-selection bias can arise from human subjects volunteering to participate in a study. Inmates motivated to sign up for a recidivism-reducing program, for example, could represent a population less likely to commit future crimes than the general inmate population. This would skew results.4
A more subtle sampling problem is recall bias, involving the malleability of human subjects' memories. In 1993, Edward Giovannucci asked an age-matched group of women, some of whom had been diagnosed with cancer, about their past dietary habits. The same women had taken a survey on dietary habits prior to their cancer diagnoses. What Giovannucci discovered was that women without cancer diagnoses recalled their diet accurately, but women with breast cancer reported consuming more fats than they had previously reported—unconsciously providing a possible (though inaccurate) explanation for their cancer.5
Ask:
- What is a dataset actually sampling?
- How many levels of sampling are present?
- What bias might be introduced at each level of sampling?
- Is the proxy measurement used (whether biomarker or online poll or bullet hole) showing actual correlation or causation?
- What might be missing from the sample and the sampling method?
The Fairness module in Machine Learning Crash Course covers ways to evaluate for and mitigate additional sources of bias in demographic datasets.
Definitions and rankings
Define terms clearly and precisely, or ask about clear and precise definitions. This is necessary to understand what data features are under consideration and what exactly is being predicted or claimed. Charles Wheelan, in Naked Statistics, offers "the health of US manufacturing" as an example of an ambiguous term. Whether US manufacturing is "healthy" or not depends entirely on how the term is defined. Greg Ip's March 2011 article in The Economist illustrates this ambiguity. If the metric for "health" is "manufacturing output," then in 2011, US manufacturing was increasingly healthy. If the "health" metric is defined as "manufacturing jobs," however, US manufacturing was on the decline.6
Rankings often suffer from similar issues, including obscured or nonsensical weights given to various components of the ranking, rankers' inconsistency, and invalid options. Malcolm Gladwell, writing in The New Yorker, mentions a Michigan supreme court chief justice, Thomas Brennan, who once sent a survey to a hundred lawyers asking them to rank ten law schools by quality, some famous, some not. Those lawyers ranked Penn State's law school in approximately fifth place, although at the time of the survey, Penn State didn't have a law school.7 Many well-known rankings include a similarly subjective reputational component. Ask what components go into a ranking, and why those components were assigned their particular weights.
Small numbers and large effects
It's not surprising to get 100% heads or 100% tails if you're flipping a coin twice. Nor is it surprising to get 25% heads after flipping a coin four times, then 75% heads for the next four flips, though that demonstrates an apparently enormous increase (that could be erroneously attributed to a sandwich eaten between the sets of coin flips, or any other spurious factor). But as the number of coin flips increases, say to 1,000 or 2,000, large percentage deviations from the expected 50% become vanishingly unlikely.
The number of measurements or experimental subjects in a study is often referred to as N. Large proportional changes due to chance are much more likely to occur in datasets and samples with a low N.
When conducting an analysis or documenting a dataset in a Data Card, specify N, so other people can consider the influence of noise and randomness.
Because model quality tends to scale with number of examples, a dataset with low N tends to result in low-quality models.
Regression to the mean
Similarly, any measurement that has some influence from chance is subject to an effect known as regression to the mean. This describes how the measurement after a particularly extreme measurement is, on average, likely to be less extreme, or closer to the mean, due to how unlikely it was for the extreme measurement to occur in the first place. The effect is more pronounced if a particularly above-average or below-average group was selected for observation, whether that group is the tallest people in a population, the worst athletes on a team, or those most at risk for stroke. The children of the tallest people are on average likely to be shorter than their parents, the worst athletes are likely to perform better after an exceptionally bad season, and those most at risk for stroke are likely to show reduced risk after any intervention or treatment, not because of causative factors but because of the properties and probabilities of randomness.
One mitigation for the effects of regression to the mean, when exploring interventions or treatments for an above-average or below-average group, is to divide the subjects into a study group and a control group in order to isolate causative effects. In the ML context, this phenomenon suggests paying extra attention to any model that predicts exceptional or outlier values, such as:
- extreme weather or temperatures
- best-performing stores or athletes
- most popular videos on a website
If a model's ongoing predictions of these exceptional values over time don't match reality, for example predicting that a highly successful store or video will continue to be successful when in fact it isn't, ask:
- Could regression to the mean be the issue?
- Are the features with the highest weights in fact more predictive than features with lower weights?
- Does collecting data that has the baseline value for those features, often zero (effectively a control group) change the model's predictions?
References
Huff, Darrell. How to Lie with Statistics. NY: W.W. Norton, 1954.
Jones, Ben. Avoiding Data Pitfalls. Hoboken, NJ: Wiley, 2020.
O'Connor, Cailin and James Owen Weatherall. The Misinformation Age. New Haven: Yale UP, 2019.
Ringler, Adam, David Mason, Gabi Laske, and Mary Templeton. "Why Do My Squiggles Look Funny? A Gallery of Compromised Seismic Signals." Seismological Research Letters 92 no. 6 (July 2021). DOI: 10.1785/0220210094
Weintraub, William S, Thomas F. Lüscher, and Stuart Pocock. "The perils of surrogate endpoints." European Heart Journal 36 no. 33 (Sep 2015): 2212–2218. DOI: 10.1093/eurheartj/ehv164
Wheelan, Charles. Naked Statistics: Stripping the Dread from the Data. NY: W.W. Norton, 2013
Image reference
"Survivorship bias." Martin Grandjean, McGeddon, and Cameron Moll 2021. CC BY-SA 4.0. Source
-
Jones 25-29. ↩
-
O'Connor and Weatherall 22-3. ↩
-
Ringling et al. ↩
-
Wheelan 120. ↩
-
Siddhartha Mukherjee, "Do Cellphones Cause Brain Cancer?" in The New York Times, April 13, 2011. Cited in Wheelan 122. ↩
-
Wheelan 39-40. ↩
-
Malcolm Gladwell, "The Order of Things", in The New Yorker Feb 14, 2011. Cited in Wheelan 56. ↩