למטרות המסמך הזה:
המטרה הסופית של פיתוח למידת מכונה היא למקסם את התועלת של המודל שנפרס.
בדרך כלל אפשר להשתמש באותם שלבים ועקרונות בסיסיים שמופיעים בקטע הזה לכל בעיה של למידת מכונה.
ההנחות בקטע הזה:
- כבר יש לכם צינור אימון שפועל באופן מלא, וגם הגדרה שמניבה תוצאה סבירה.
- יש לכם מספיק משאבי מחשוב כדי לבצע ניסויים משמעותיים של התאמה וכדי להריץ לפחות כמה משימות אימון במקביל.
אסטרטגיית הכוונון המצטבר
המלצה: כדאי להתחיל עם הגדרה פשוטה. לאחר מכן, מבצעים שיפורים בהדרגה תוך כדי קבלת תובנות לגבי הבעיה. חשוב לוודא שכל שיפור מבוסס על ראיות חזקות.
אנחנו מניחים שהמטרה שלך היא למצוא הגדרה שתמקסם את הביצועים של המודל. לפעמים המטרה היא לשפר את המודל כמה שיותר עד למועד סיום קבוע. במקרים אחרים, אפשר להמשיך לשפר את המודל ללא הגבלה. לדוגמה, שיפור מתמשך של מודל שנמצא בשימוש בייצור.
באופן עקרוני, אפשר למקסם את הביצועים באמצעות אלגוריתם שמחפש באופן אוטומטי את כל מרחב ההגדרות האפשריות, אבל זו לא אפשרות מעשית. מרחב התצורות האפשריות הוא גדול מאוד, ועדיין אין אלגוריתמים מתוחכמים מספיק כדי לחפש ביעילות במרחב הזה ללא הנחיה אנושית. רוב האלגוריתמים האוטומטיים לחיפוש מסתמכים על מרחב חיפוש שתוכנן באופן ידני ומגדיר את קבוצת ההגדרות לחיפוש, והגדרת מרחבי החיפוש האלה יכולה להיות חשובה מאוד.
הדרך היעילה ביותר למקסם את הביצועים היא להתחיל עם הגדרה פשוטה, להוסיף תכונות בהדרגה ולבצע שיפורים תוך כדי צבירת תובנות לגבי הבעיה.
מומלץ להשתמש באלגוריתמים אוטומטיים לחיפוש בכל סבב של שיפורים, ולעדכן באופן שוטף את מרחבי החיפוש ככל שההבנה שלכם מתרחבת. במהלך השימוש, תגלו באופן טבעי תצורות טובות יותר ויותר, ולכן המודל ה "הכי טוב" שלכם ישתפר כל הזמן.
המונח 'השקה' מתייחס לעדכון של ההגדרה הכי טובה שלנו (שיכול להיות שתתאים או לא תתאים להשקה בפועל של מודל לייצור). לפני כל 'השקה', חשוב לוודא שהשינוי מבוסס על ראיות חזקות – ולא רק על סיכוי אקראי שמבוסס על הגדרה שהצליחה במקרה – כדי שלא תהיה מורכבות מיותרת בצינור ההדרכה.
באופן כללי, אסטרטגיית ההתאמה ההדרגתית שלנו כוללת חזרה על ארבעת השלבים הבאים:
- בוחרים יעד לסיבוב הבא של הניסויים. חשוב לוודא שהיעד מוגדר בהיקף המתאים.
- תכנון סבב הניסויים הבא. לתכנן ולבצע סדרה של ניסויים שיובילו להשגת היעד הזה.
- לומדים מהתוצאות של הניסוי. הערכת הניסוי באמצעות רשימת משימות.
- קובעים אם לאמץ את השינוי המוצע.
בהמשך הקטע הזה מפורטת האסטרטגיה הזו.
בחירת יעד לסיבוב הבא של הניסויים
אם תנסו להוסיף כמה תכונות או לענות על כמה שאלות בבת אחת, יכול להיות שלא תוכלו להפריד בין ההשפעות השונות על התוצאות. דוגמאות ליעדים:
- לנסות שיפור פוטנציאלי של הצינור (לדוגמה, רגולריזטור חדש, בחירה של עיבוד מקדים וכו').
- להבין את ההשפעה של היפר-פרמטר מסוים של המודל (לדוגמה, פונקציית ההפעלה)
- מצמצמים את שגיאת האימות.
עדיפות להתקדמות לטווח ארוך על פני שיפורים בשגיאות אימות לטווח קצר
סיכום: ברוב המקרים, המטרה העיקרית היא לקבל תובנות לגבי בעיית ההתאמה.
מומלץ להקדיש את רוב הזמן להבנת הבעיה, ולהקדיש יחסית מעט זמן לניסיון למקסם את הביצועים בקבוצת האימות. במילים אחרות, כדאי להשקיע את רוב הזמן ב'חיפוש' ורק חלק קטן ב'ניצול'. כדי למקסם את הביצועים הסופיים, חשוב להבין את הבעיה. התמקדות בתובנות במקום ברווחים לטווח קצר עוזרת:
- כדאי להימנע מהשקת שינויים מיותרים שהיו קיימים במקרה בהרצות עם ביצועים טובים, רק בגלל צירוף מקרים היסטורי.
- לזהות את ההיפרפרמטרים שהשגיאה באימות הכי רגישה להם, את ההיפרפרמטרים שיש ביניהם הכי הרבה אינטראקציות ולכן צריך לכוונן אותם מחדש ביחד, ואת ההיפרפרמטרים שהם יחסית לא רגישים לשינויים אחרים ולכן אפשר לתקן אותם בניסויים עתידיים.
- להציע תכונות חדשות פוטנציאליות לניסיון, כמו שיטות רגולריזציה חדשות אם יש בעיה של התאמת יתר.
- לזהות תכונות שלא עוזרות ולכן אפשר להסיר אותן, וכך להפחית את המורכבות של ניסויים עתידיים.
- לזהות מתי סביר להניח שהשיפורים שמתקבלים מכוונון היפר-פרמטרים הגיעו לנקודת מיצוי.
- כדי לשפר את יעילות ההתאמה, כדאי לצמצם את מרחבי החיפוש סביב הערך האופטימלי.
בסופו של דבר תבינו את הבעיה. אחר כך תוכלו להתמקד רק בשגיאת האימות, גם אם הניסויים לא מספקים מידע רב על מבנה בעיית ההתאמה.
תכנון סבב הניסויים הבא
סיכום: זיהוי ההיפר-פרמטרים המדעיים, המפריעים והקבועים עבור היעד של הניסוי. יוצרים רצף של מחקרים כדי להשוות בין ערכים שונים של היפרפרמטרים מדעיים, תוך אופטימיזציה של היפרפרמטרים מפריעים. בוחרים את מרחב החיפוש של היפרפרמטרים מטרידים כדי לאזן בין עלויות המשאבים לבין הערך המדעי.
זיהוי היפרפרמטרים מדעיים, היפרפרמטרים שקשורים לבעיות והיפרפרמטרים קבועים
לכל יעד נתון, כל ההיפרפרמטרים נכללים באחת מהקטגוריות הבאות:
- היפרפרמטרים מדעיים הם פרמטרים שההשפעה שלהם על הביצועים של המודל היא מה שאתם מנסים למדוד.
- היפרפרמטרים של רעשי רקע הם היפרפרמטרים שצריך לבצע אופטימיזציה שלהם כדי להשוות בצורה הוגנת בין ערכים שונים של ההיפרפרמטרים המדעיים. היפר-פרמטרים מטרידים דומים לפרמטרים מטרידים בסטטיסטיקה.
- להיפרפרמטרים קבועים יש ערכים קבועים בסבב הנוכחי של הניסויים. הערכים של היפרפרמטרים קבועים לא צריכים להשתנות כשמשווים בין ערכים שונים של היפרפרמטרים מדעיים. אם קובעים ערכים מסוימים להיפרפרמטרים עבור קבוצה של ניסויים, צריך להביא בחשבון שהמסקנות שיוסקו מהניסויים האלה לא בהכרח יהיו תקפות להגדרות אחרות של ההיפרפרמטרים הקבועים. במילים אחרות, היפרפרמטרים קבועים יוצרים מגבלות על כל המסקנות שאתם מסיקים מהניסויים.
לדוגמה, נניח שהיעד שלכם הוא:
האם למודל עם יותר שכבות מוסתרות יש שגיאת אימות נמוכה יותר.
במקרה זה:
- קצב הלמידה הוא פרמטר-על בעייתי כי אפשר להשוות בין מודלים עם מספרים שונים של שכבות מוסתרות רק אם קצב הלמידה מותאם בנפרד לכל מספר של שכבות מוסתרות. (שיעור הלמידה האופטימלי בדרך כלל תלוי בארכיטקטורת המודל).
- פונקציית ההפעלה יכולה להיות היפרפרמטר קבוע אם קבעתם בניסויים קודמים שפונקציית ההפעלה הטובה ביותר לא רגישה לעומק המודל. לחלופין, אפשר להגביל את המסקנות לגבי מספר השכבות הנסתרות כדי לכסות את פונקציית ההפעלה הזו. לחלופין, יכול להיות שזה יהיה היפרפרמטר מעצבן אם אתם מוכנים לכוון אותו בנפרד לכל מספר של שכבות מוסתרות.
היפר-פרמטר מסוים יכול להיות היפר-פרמטר מדעי, היפר-פרמטר של רעשי רקע או היפר-פרמטר קבוע. הסיווג של ההיפר-פרמטר משתנה בהתאם ליעד הניסוי. לדוגמה, פונקציית ההפעלה יכולה להיות כל אחת מהאפשרויות הבאות:
- פרמטר היפר-פרמטר מדעי: האם ReLU או tanh הם בחירה טובה יותר לבעיה שלנו?
- פרמטר היפר בעייתי: האם המודל הטוב ביותר עם חמש שכבות טוב יותר מהמודל הטוב ביותר עם שש שכבות כשמאפשרים כמה פונקציות הפעלה שונות?
- היפרפרמטר קבוע: ברשתות ReLU, האם הוספת נורמליזציה של קבוצות מידע במיקום מסוים עוזרת?
כשמתכננים סבב חדש של ניסויים:
- מזהים את ההיפרפרמטרים המדעיים של היעד הניסויי. (בשלב הזה, אפשר להתייחס לכל הפרמטרים האחרים כפרמטרים מעצבנים).
- המרת חלק מההיפר-פרמטרים המיותרים להיפר-פרמטרים קבועים.
אם היו לכם משאבים בלתי מוגבלים, הייתם משאירים את כל ההיפר-פרמטרים הלא מדעיים כהיפר-פרמטרים מטרידים, כדי שהמסקנות שתסיקו מהניסויים לא יכללו אזהרות לגבי ערכי היפר-פרמטרים קבועים. עם זאת, ככל שמנסים לכוונן יותר היפרפרמטרים של רעשי רקע, כך גדל הסיכון שלא תצליחו לכוונן אותם בצורה מספיק טובה לכל הגדרה של ההיפרפרמטרים המדעיים, ובסופו של דבר תגיעו למסקנות שגויות מהניסויים. כפי שמתואר בקטע בהמשך, אפשר להקטין את הסיכון הזה על ידי הגדלת התקציב החישובי. עם זאת, התקציב המקסימלי של המשאבים שלכם לרוב נמוך מהתקציב שנדרש כדי לכוונן את כל ההיפרפרמטרים הלא-מדעיים.
מומלץ להמיר פרמטר היפר-פרמטר מפריע לפרמטר היפר-פרמטר קבוע אם החסרונות שנובעים מהקיבוע שלו פחות משמעותיים מהעלות של הכללתו כפרמטר היפר-פרמטר מפריע. ככל שפרמטר היפר-פרמטר מפריע יותר לאינטראקציה עם ההיפר-פרמטרים המדעיים, כך הנזק שייגרם מתיקון הערך שלו יהיה גדול יותר. לדוגמה, הערך הטוב ביותר של עוצמת דעיכת המשקל תלוי בדרך כלל בגודל המודל, ולכן השוואה בין גדלים שונים של מודלים בהנחה של ערך ספציפי יחיד של דעיכת המשקל לא תהיה מועילה במיוחד.
חלק מהפרמטרים של הכלי לאופטימיזציה
ככלל, חלק מההיפר-פרמטרים של האופטימיזציה (למשל, קצב הלמידה, המומנטום, פרמטרים של תזמון קצב הלמידה, בטא של Adam וכו') הם היפר-פרמטרים מפריעים כי הם נוטים ליצור אינטראקציה עם שינויים אחרים. היפרפרמטרים של אופטימיזציה הם בדרך כלל לא היפרפרמטרים מדעיים, כי מטרה כמו 'מהו קצב הלמידה הטוב ביותר לצינור הנוכחי?' לא מספקת תובנות רבות. בכל מקרה, יכול להיות שההגדרה הכי טובה תשתנה אחרי השינוי הבא בצינור.
יכול להיות שתצטרכו לתקן מדי פעם חלק מהיפרפרמטרים של האופטימיזציה בגלל מגבלות משאבים או בגלל ראיות חזקות במיוחד לכך שהם לא משפיעים על הפרמטרים המדעיים. עם זאת, בדרך כלל צריך להניח שצריך לכוון את ההיפר-פרמטרים של האופטימיזציה בנפרד כדי להשוות בצורה הוגנת בין הגדרות שונות של ההיפר-פרמטרים המדעיים, ולכן לא כדאי לקבע אותם. בנוסף, אין סיבה מראש להעדיף ערך היפרפרמטר אחד של אופטימיזציה על פני ערך אחר. לדוגמה, ערכי היפרפרמטר של אופטימיזציה בדרך כלל לא משפיעים על העלות החישובית של העברות קדימה או של שיפועים.
בחירת הכלי לאופטימיזציה
בדרך כלל יש שתי אפשרויות לבחירה של כלי אופטימיזציה:
- היפר-פרמטר מדעי
- היפר-פרמטר קבוע
פרמטר אופטימיזציה הוא היפר-פרמטר מדעי אם המטרה של הניסוי היא לבצע השוואות הוגנות בין שני פרמטרים שונים של אופטימיזציה או יותר. לדוגמה:
קובעים איזה כלי אופטימיזציה מפיק את שגיאת האימות הנמוכה ביותר במספר נתון של שלבים.
לחלופין, אפשר להגדיר את האופטימיזציה כהיפרפרמטר קבוע מסיבות שונות, כולל:
- ניסויים קודמים מצביעים על כך שהאופטימיזציה הטובה ביותר לבעיית ההתאמה שלך לא רגישה להיפרפרמטרים מדעיים נוכחיים.
- אתם מעדיפים להשוות בין הערכים של ההיפרפרמטרים המדעיים באמצעות האופטימיזציה הזו, כי קל יותר להסיק מסקנות מהעקומות של האימון שלה.
- אתם מעדיפים להשתמש בכלי האופטימיזציה הזה כי הוא משתמש בפחות זיכרון מהחלופות.
היפר-פרמטרים של רגולריזציה
היפר-פרמטרים שנוצרים על ידי טכניקת רגולריזציה הם בדרך כלל היפר-פרמטרים שוליים. עם זאת, ההחלטה אם לכלול את טכניקת הרגולריזציה היא היפרפרמטר מדעי או קבוע.
לדוגמה, רגולריזציה של נשירה מוסיפה מורכבות לקוד. לכן, כשמחליטים אם לכלול dropout regularization, אפשר להגדיר את ההיפר-פרמטרים 'no dropout' לעומת 'dropout' כהיפר-פרמטרים מדעיים, ואת dropout rate כהיפר-פרמטר מפריע. אם תחליטו להוסיף רגולריזציה של dropout לצנרת על סמך הניסוי הזה, שיעור ה-dropout יהיה היפרפרמטר מפריע בניסויים עתידיים.
היפר-פרמטרים אדריכליים
היפר-פרמטרים ארכיטקטוניים הם לרוב היפר-פרמטרים מדעיים או קבועים, כי שינויים בארכיטקטורה יכולים להשפיע על עלויות ההצגה והאימון, על זמן האחזור ועל דרישות הזיכרון. לדוגמה, מספר השכבות הוא בדרך כלל היפרפרמטר מדעי או קבוע, כי יש לו השפעה משמעותית על מהירות האימון והשימוש בזיכרון.
תלויות בהיפר-פרמטרים מדעיים
במקרים מסוימים, קבוצות ההיפר-פרמטרים הקבועים וההיפר-פרמטרים שמשפיעים על הרעש תלויות בערכים של ההיפר-פרמטרים המדעיים. לדוגמה, נניח שאתם מנסים לקבוע איזה אופטימיזטור במומנטום של נסטרוב וב-Adam מניב את שגיאת האימות הנמוכה ביותר. במקרה זה:
- ההיפרפרמטר המדעי הוא האופטימיזציה, שמקבל ערכים
{"Nesterov_momentum", "Adam"} - הערך
optimizer="Nesterov_momentum"מציג את ההיפרפרמטרים{learning_rate, momentum}, שיכולים להיות היפרפרמטרים קבועים או היפרפרמטרים שמשתנים. - הערך
optimizer="Adam"מציג את ההיפר-פרמטרים{learning_rate, beta1, beta2, epsilon}, שיכולים להיות היפר-פרמטרים קבועים או היפר-פרמטרים שמשתנים.
היפר-פרמטרים שמופיעים רק עבור ערכים מסוימים של ההיפר-פרמטרים המדעיים נקראים היפר-פרמטרים מותנים.
אל תניחו ששני היפר-פרמטרים מותנים זהים רק בגלל שיש להם את אותו שם. בדוגמה שלמעלה, ההיפר-פרמטר המותנה שנקרא learning_rate הוא היפר-פרמטר שונה עבור optimizer="Nesterov_momentum" מאשר עבור optimizer="Adam". התפקיד של המשתנה דומה (אבל לא זהה) בשני האלגוריתמים, אבל טווח הערכים שפועלים היטב בכל אחד מהאופטימיזטורים בדרך כלל שונה בכמה סדרי גודל.
יצירת קבוצה של מחקרים
אחרי שמזהים את ההיפרפרמטרים המדעיים וההיפרפרמטרים שגורמים להפרעות, צריך לתכנן מחקר או רצף של מחקרים כדי להתקדם לעבר היעד של הניסוי. מחקר מציין קבוצה של הגדרות היפר-פרמטרים להרצה לצורך ניתוח בהמשך. כל הגדרה נקראת ניסיון. יצירת מחקר בדרך כלל כוללת בחירה של האפשרויות הבאות:
- היפר-פרמטרים שמשתנים בין ניסויים.
- הערכים שהיפרפרמטרים יכולים לקבל (מרחב החיפוש).
- מספר הניסיונות.
- אלגוריתם חיפוש אוטומטי לדגימת מספר כה רב של ניסויים ממרחב החיפוש.
אפשרות אחרת היא ליצור מחקר על ידי הגדרה ידנית של קבוצת ההגדרות של ההיפרפרמטרים.
מטרת המחקרים היא לבצע בו-זמנית את הפעולות הבאות:
- מריצים את צינור העיבוד עם ערכים שונים של היפרפרמטרים מדעיים.
- אופטימיזציה של היפרפרמטרים מעצבנים (או אופטימיזציה של היפרפרמטרים) כדי שההשוואות בין ערכים שונים של היפרפרמטרים מדעיים יהיו הוגנות ככל האפשר.
במקרה הפשוט ביותר, יוצרים מחקר נפרד לכל הגדרה של הפרמטרים המדעיים, כאשר כל מחקר מבצע אופטימיזציה של היפרפרמטרים שאינם רלוונטיים. לדוגמה, אם המטרה היא לבחור את האופטימיזציה הכי טובה מבין Nesterov momentum ו-Adam, אפשר ליצור שני מחקרים:
- מחקר אחד שבו
optimizer="Nesterov_momentum"והיפרפרמטרים של רעשי רקע הם{learning_rate, momentum} - מחקר נוסף שבו
optimizer="Adam"והיפרפרמטרים של רעשי רקע הם{learning_rate, beta1, beta2, epsilon}.
כדי להשוות בין שני כלי האופטימיזציה, בוחרים את הניסוי שמניב את הביצועים הכי טובים מכל מחקר.
אתם יכולים להשתמש בכל אלגוריתם אופטימיזציה ללא גרדיאנט, כולל שיטות כמו אופטימיזציה בייסיאנית או אלגוריתמים אבולוציוניים, כדי לבצע אופטימיזציה של היפרפרמטרים מפריעים. עם זאת, אנחנו מעדיפים להשתמש בחיפוש אקראי למחצה בשלב הניסוי והטעייה של ההתאמה, בגלל היתרונות הרבים שיש לו בהגדרה הזו. אחרי שמסיימים את הניתוח, מומלץ להשתמש בתוכנה מתקדמת לאופטימיזציה בייסיאנית (אם היא זמינה).
נניח שאתם רוצים להשוות בין מספר גדול של ערכים של ההיפר-פרמטרים המדעיים, אבל לא מעשי לבצע כל כך הרבה מחקרים עצמאיים. במקרה כזה, אפשר לבצע את הפעולות הבאות:
- כוללים את הפרמטרים המדעיים באותו מרחב חיפוש כמו ההיפר-פרמטרים של הרעש.
- שימוש באלגוריתם חיפוש כדי לדגום ערכים של ההיפר-פרמטרים המדעיים ושל ההיפר-פרמטרים המפריעים במחקר יחיד.
כשמשתמשים בגישה הזו, היפרפרמטרים מותנים עלולים לגרום לבעיות. בסופו של דבר, קשה לציין מרחב חיפוש אלא אם קבוצת ההיפרפרמטרים המפריעים זהה לכל הערכים של ההיפרפרמטרים המדעיים. במקרה כזה, אנחנו מעדיפים להשתמש בחיפוש אקראי למחצה במקום בכלי אופטימיזציה מתוחכמים יותר של קופסה שחורה, כי הוא מבטיח דגימה אחידה של ערכים שונים של היפרפרמטרים מדעיים. לא משנה מהו אלגוריתם החיפוש, צריך לוודא שהוא מחפש את הפרמטרים המדעיים באופן אחיד.
איזון בין ניסויים אינפורמטיביים לניסויים במחיר סביר
כשמתכננים מחקר או סדרת מחקרים, צריך להקצות תקציב מוגבל כדי להשיג את שלוש המטרות הבאות:
- השוואה בין מספיק ערכים שונים של היפרפרמטרים מדעיים.
- כוונון של היפרפרמטרים מעצבנים במרחב חיפוש גדול מספיק.
- דגימה של מרחב החיפוש של היפר-פרמטרים מטרידים בצפיפות מספקת.
ככל שתצליחו יותר להשיג את שלושת היעדים האלה, כך תוכלו להפיק יותר תובנות מהניסוי. השוואה של כמה שיותר ערכים של היפרפרמטרים מדעיים מרחיבה את היקף התובנות שאפשר להפיק מהניסוי.
הכללה של כמה שיותר היפר-פרמטרים מפריעים והגדרה של טווח רחב ככל האפשר לכל היפר-פרמטר מפריע מגדילה את הסיכוי למצוא ערך 'טוב' של ההיפר-פרמטרים המפריעים במרחב החיפוש של כל הגדרה של ההיפר-פרמטרים המדעיים. אחרת, יכול להיות שתבצעו השוואות לא הוגנות בין ערכים של היפרפרמטרים מדעיים, כי לא תבצעו חיפוש באזורים אפשריים של מרחב ההיפרפרמטרים המפריעים, שבהם יכולים להיות ערכים טובים יותר עבור חלק מהערכים של הפרמטרים המדעיים.
דוגמים את מרחב החיפוש של היפר-פרמטרים מפריעים בצפיפות גבוהה ככל האפשר. הפעולה הזו מגדילה את הסיכוי שתהליך החיפוש ימצא הגדרות טובות להיפרפרמטרים המיותרים שקיימים במרחב החיפוש. אחרת, יכול להיות שתבצעו השוואות לא הוגנות בין ערכים של הפרמטרים המדעיים, כי חלק מהערכים יקבלו דגימה מוצלחת יותר של היפר-פרמטרים מפריעים.
לצערנו, כדי לשפר את אחד משלושת המאפיינים האלה צריך לבצע אחת מהפעולות הבאות:
- הגדלת מספר הניסויים, ולכן הגדלת עלות המשאבים.
- למצוא דרך לחסוך במשאבים באחד מהמימדים האחרים.
לכל בעיה יש מאפיינים ייחודיים ומגבלות חישוביות משלה, ולכן הקצאת משאבים לשלושת היעדים האלה דורשת ידע מסוים בתחום. אחרי שמריצים מחקר, תמיד כדאי לנסות להבין אם המחקר כוונן את ההיפר-פרמטרים המפריעים בצורה מספיק טובה. כלומר, המחקר חיפש מרחב גדול מספיק באופן מקיף מספיק כדי להשוות בצורה הוגנת את ההיפר-פרמטרים המדעיים (כפי שמתואר בפירוט רב יותר בקטע הבא).
לומדים מהתוצאות של הניסוי
המלצה: בנוסף לניסיון להשיג את המטרה המדעית המקורית של כל קבוצת ניסויים, כדאי לעבור על רשימת שאלות נוספות. אם אתם מגלים בעיות, כדאי לשנות את הניסויים ולהריץ אותם מחדש.
בסופו של דבר, לכל קבוצת ניסויים יש מטרה ספציפית. כדאי לבחון את הנתונים שהניסויים מספקים כדי להבין אם אתם מתקדמים לעבר המטרה. עם זאת, אם שואלים את השאלות הנכונות, אפשר לרוב למצוא בעיות ולתקן אותן לפני שקבוצה מסוימת של ניסויים יכולה להתקדם לעבר המטרה המקורית שלה. אם לא תשאל את השאלות האלה, יכול להיות שתסיק מסקנות שגויות.
הפעלת ניסויים עלולה להיות יקרה, ולכן כדאי גם להפיק תובנות שימושיות אחרות מכל קבוצת ניסויים, גם אם התובנות האלה לא רלוונטיות באופן מיידי למטרה הנוכחית.
לפני שמנתחים קבוצה מסוימת של ניסויים כדי להתקדם לעבר היעד המקורי שלהם, כדאי לשאול את עצמכם את השאלות הנוספות הבאות:
- האם מרחב החיפוש גדול מספיק? אם הנקודה האופטימלית ממחקר מסוים קרובה לגבול של מרחב החיפוש בממד אחד או יותר, כנראה שהחיפוש לא רחב מספיק. במקרה כזה, כדאי להריץ מחקר נוסף עם מרחב חיפוש מורחב.
- האם דגמת מספיק נקודות ממרחב החיפוש? אם לא, כדאי להריץ עוד נקודות או להגדיר יעדים פחות שאפתניים.
- איזה חלק מהניסויים בכל מחקר לא אפשריים? כלומר, אילו ניסויים סוטים, מקבלים ערכי הפסד גרועים מאוד או לא מצליחים לפעול בכלל כי הם מפרים אילוץ מרומז כלשהו? אם חלק גדול מאוד מהנקודות במחקר לא אפשריות, צריך לשנות את מרחב החיפוש כדי להימנע מדגימה של נקודות כאלה. לפעמים צריך לשנות את הפרמטרים של מרחב החיפוש. במקרים מסוימים, מספר גדול של נקודות לא אפשריות יכול להצביע על באג בקוד ההדרכה.
- האם המודל מציג בעיות אופטימיזציה?
- מה אפשר ללמוד מעקומות האימון של הניסויים הכי טובים? לדוגמה, האם לניסויים הטובים ביותר יש עקומות אימון שתואמות לבעיות של התאמת יתר?
אם יש צורך, על סמך התשובות לשאלות הקודמות, משפרים את המחקר האחרון או את קבוצת המחקרים כדי להרחיב את מרחב החיפוש ו/או להגדיל את מדגם הניסויים, או מבצעים פעולה מתקנת אחרת.
אחרי שעונים על השאלות שלמעלה, אפשר להעריך את הנתונים שהניסויים מספקים ביחס ליעד המקורי. לדוגמה, הערכה של התועלת של שינוי מסוים.
זיהוי גבולות לא טובים של מרחב החיפוש
מרחב חיפוש נחשב לחשוד אם הנקודה הכי טובה שנדגמה ממנו קרובה לגבול שלו. אפשר להרחיב את טווח החיפוש בכיוון הזה כדי למצוא נקודה טובה יותר.
כדי לבדוק את הגבולות של מרחב החיפוש, מומלץ לשרטט ניסויים שהושלמו בתרשימים בסיסיים של ציר ההיפרפרמטרים. בגרפים האלה, אנחנו משרטטים את ערך היעד של האימות לעומת אחד מהיפר-פרמטרים (לדוגמה, קצב הלמידה). כל נקודה בתרשים מתאימה לניסיון אחד.
ערך יעד האימות של כל ניסוי צריך להיות בדרך כלל הערך הכי טוב שהושג במהלך האימון.
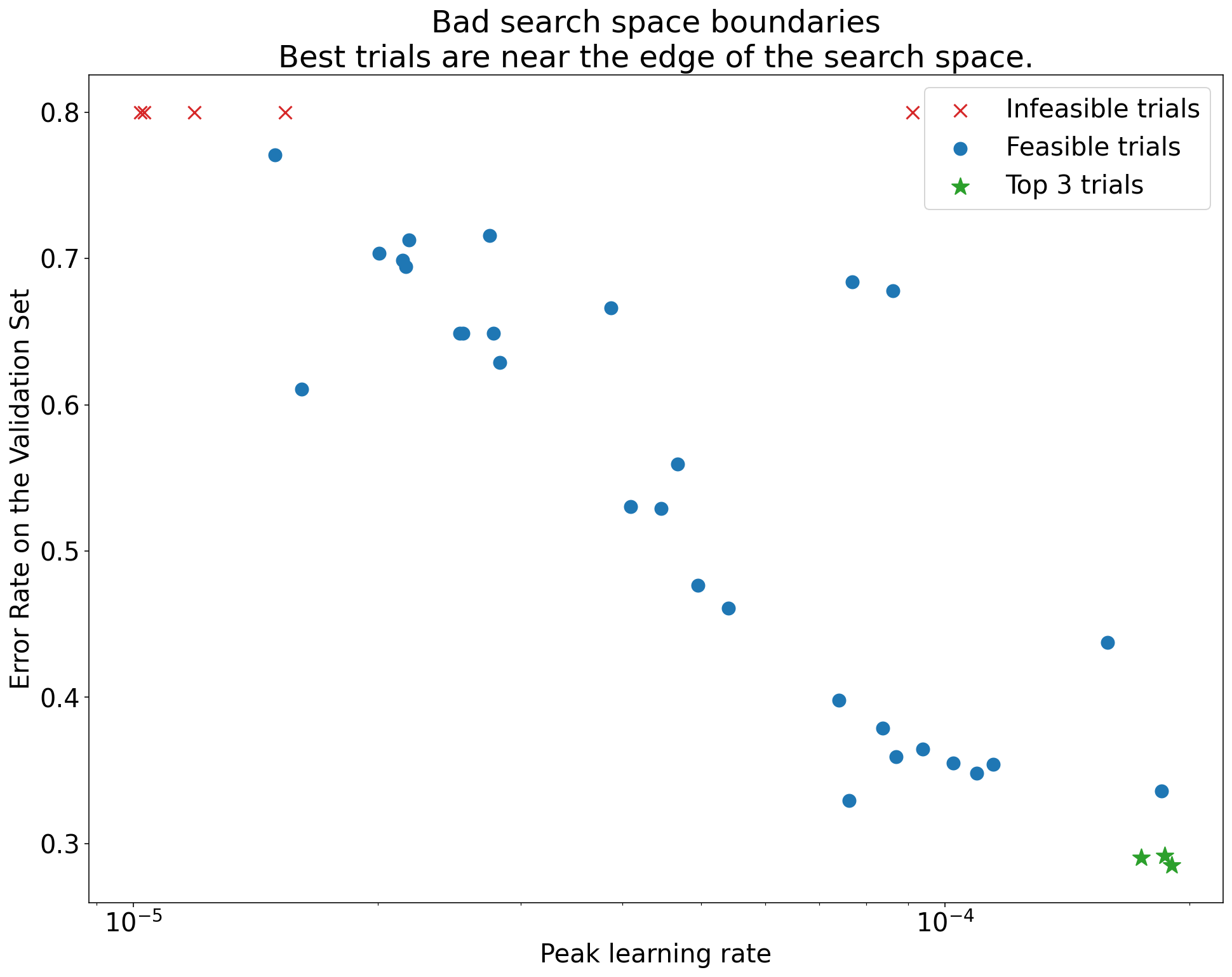
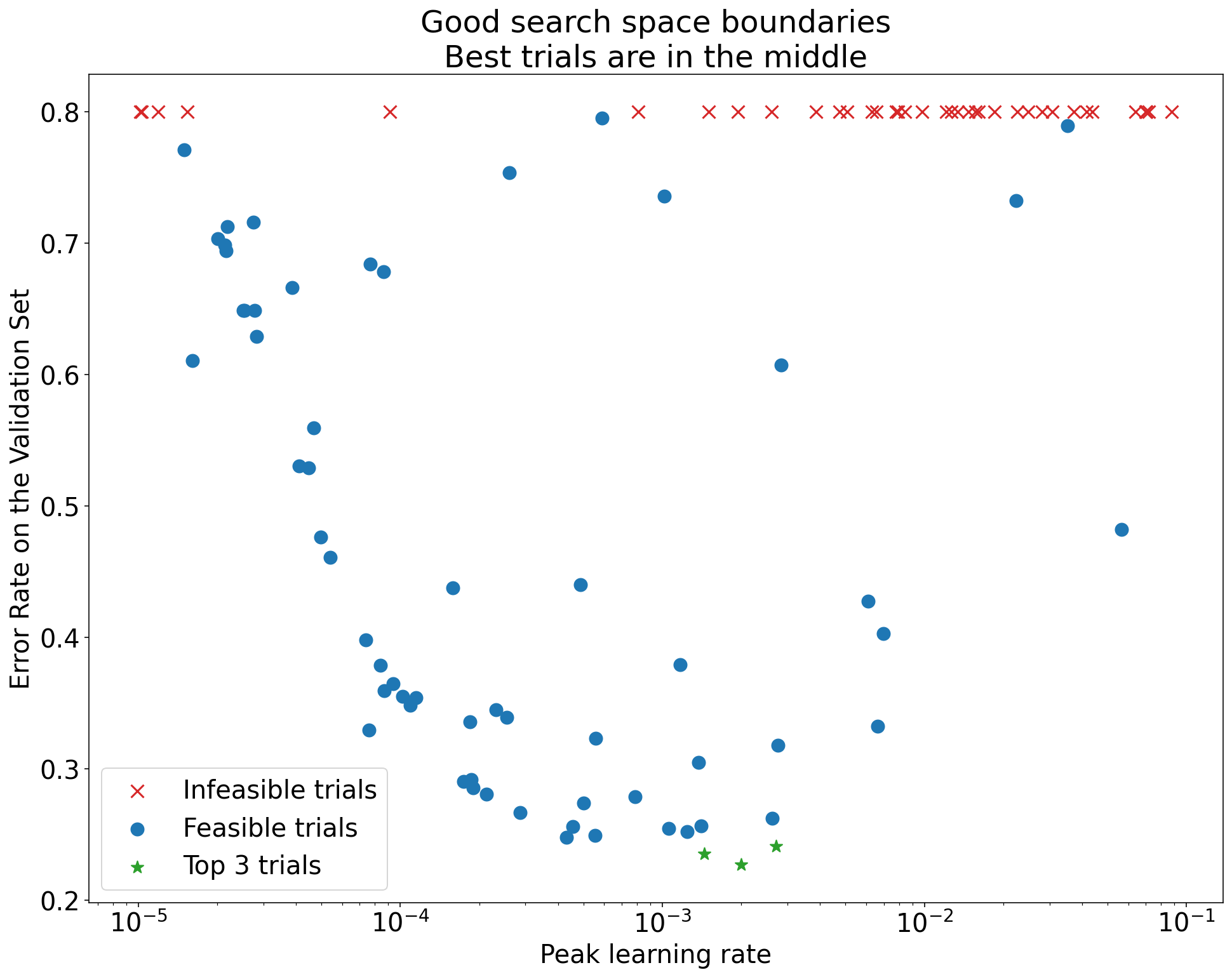
איור 1: דוגמאות לגבולות לא תקינים של מרחב חיפוש ולגבולות תקינים של מרחב חיפוש.
התרשימים באיור 1 מציגים את שיעור השגיאה (ערך נמוך יותר טוב יותר) לעומת שיעור הלמידה הראשוני. אם הנקודות הכי טובות מתקבצות לקצה של מרחב החיפוש (במאפיין מסוים), יכול להיות שתצטרכו להרחיב את הגבולות של מרחב החיפוש עד שהנקודה הכי טובה שנצפתה לא תהיה יותר קרובה לגבול.
בדרך כלל, מחקר כולל ניסויים 'לא מעשיים' שמתפצלים או מניבים תוצאות גרועות מאוד (מסומנים ב-X אדום באיור 1). אם כל הניסויים לא מתאימים לשיעורי למידה שגבוהים מערך סף מסוים, ואם שיעורי הלמידה בניסויים עם הביצועים הכי טובים נמצאים בקצה של האזור הזה, יכול להיות שהמודל סובל מבעיות יציבות שמונעות ממנו לגשת לשיעורי למידה גבוהים יותר.
לא נדגמות מספיק נקודות במרחב החיפוש
באופן כללי, יכול להיות מאוד קשה לדעת אם מרחב החיפוש נדגם בצפיפות מספקת. 🤖 עדיף להריץ יותר ניסויים מאשר פחות, אבל יותר ניסויים יוצרים עלות נוספת ברורה.
קשה לדעת מתי דגמתם מספיק נתונים, ולכן אנחנו ממליצים:
- לבדוק מה אתם יכולים להרשות לעצמכם.
- כיול של רמת הביטחון האינטואיטיבית על ידי התבוננות חוזרת בגרפים של ציר ההיפרפרמטרים השונים וניסיון להבין כמה נקודות נמצאות באזור ה "טוב" של מרחב החיפוש.
בדיקת עקומות האימון
סיכום: בדיקת עקומות ההפסד היא דרך קלה לזהות מצבי כשל נפוצים, והיא יכולה לעזור לכם לתעדף פעולות אפשריות.
במקרים רבים, כדי להשיג את המטרה העיקרית של הניסויים, צריך רק להתייחס לשגיאת האימות של כל ניסיון. עם זאת, צריך להיזהר כשמצמצמים כל ניסיון למספר יחיד, כי המיקוד הזה עלול להסתיר פרטים חשובים על מה שקורה מתחת לפני השטח. בכל מחקר, מומלץ מאוד לעיין בעקומות ההפסד של כמה מהניסויים הטובים ביותר לפחות. גם אם זה לא הכרחי כדי להשיג את המטרה העיקרית של הניסוי, בדיקת עקומות ההפסד (כולל הפסד האימון והפסד האימות) היא דרך טובה לזהות מצבי כשל נפוצים, והיא יכולה לעזור לכם לקבוע אילו פעולות כדאי לבצע בהמשך.
כשבודקים את עקומות ההפסד, כדאי להתמקד בשאלות הבאות:
האם יש ניסויים שבהם יש התאמת יתר בעייתית? בעיה של התאמת יתר מתרחשת כשהשגיאה באימות מתחילה לגדול במהלך האימון. בהגדרות ניסוי שבהן מבצעים אופטימיזציה של היפרפרמטרים לא רלוונטיים על ידי בחירת הניסיון ה"טוב ביותר" לכל הגדרה של ההיפרפרמטרים המדעיים, צריך לבדוק אם יש התאמת יתר בעייתית לפחות בכל אחד מהניסיונות הטובים ביותר שמתאימים להגדרות של ההיפרפרמטרים המדעיים שמשווים ביניהם. אם באחד מהניסויים הטובים ביותר יש התאמת יתר בעייתית, אפשר לבצע את אחת מהפעולות הבאות או את שתיהן:
- מריצים מחדש את הניסוי עם טכניקות רגולריזציה נוספות
- כדאי לכוונן מחדש את פרמטרי הרגולריזציה הקיימים לפני השוואת הערכים של ההיפר-פרמטרים המדעיים. יכול להיות שההמלצה הזו לא רלוונטית אם הפרמטרים העל-מוגדרים המדעיים כוללים פרמטרים של רגולריזציה, כי אז לא מפתיע שהגדרות של הפרמטרים האלה עם עוצמה נמוכה מובילות להתאמת יתר בעייתית.
לרוב קל לצמצם את התאמת היתר באמצעות טכניקות רגולריזציה נפוצות שמוסיפות מורכבות מינימלית לקוד או חישוב נוסף (לדוגמה, רגולריזציה של נשירה, החלקת תוויות, דעיכת משקל). לכן, בדרך כלל קל להוסיף אחד או יותר מהם לסבב הבא של הניסויים. לדוגמה, אם ההיפרפרמטר המדעי הוא 'מספר השכבות הנסתרות' והניסיון הטוב ביותר שמשתמש במספר הגדול ביותר של שכבות נסתרות מציג התאמת יתר בעייתית, מומלץ לנסות שוב עם רגולריזציה נוספת במקום לבחור מיד את המספר הקטן יותר של שכבות נסתרות.
גם אם באף אחד מהניסויים 'הטובים ביותר' לא זוהה התאמת יתר בעייתית, יכול להיות שיש בעיה אם היא מתרחשת באחד מהניסויים. בחירת הניסוי הטוב ביותר מדכאת הגדרות שמציגות התאמת יתר בעייתית, ומעדיפה הגדרות שלא מציגות התאמת יתר. במילים אחרות, בחירה באפשרות 'הניסיון הטוב ביותר' מעדיפה הגדרות עם יותר רגולריזציה. עם זאת, כל דבר שפוגע באימון יכול לשמש כרגולריזטור, גם אם זו לא הייתה הכוונה. לדוגמה, בחירה של שיעור למידה קטן יותר יכולה להסדיר את האימון על ידי הגבלת תהליך האופטימיזציה, אבל בדרך כלל לא מומלץ לבחור את שיעור הלמידה בדרך הזו. חשוב לשים לב שאולי המערכת תבחר את תקופת הניסיון 'הטובה ביותר' לכל הגדרה של ההיפרפרמטרים המדעיים באופן שמעדיף ערכים 'גרועים' של חלק מההיפרפרמטרים המדעיים או המטרידים.
האם יש שונות גבוהה משלב לשלב בשגיאת האימון או האימות בשלב מאוחר באימון? אם כן, יכול להיות שהיא תשפיע על שני הדברים הבאים:
- היכולת להשוות בין ערכים שונים של היפרפרמטרים מדעיים. הסיבה לכך היא שכל תקופת ניסיון מסתיימת באופן אקראי בשלב 'מזל' או 'חוסר מזל'.
- היכולת לשחזר את התוצאה של תקופת הניסיון הטובה ביותר בסביבת הייצור. הסיבה לכך היא שאולי מודל הייצור לא יסתיים באותו שלב 'מזל' כמו במחקר.
הסיבות הסבירות ביותר לשונות בין השלבים הן:
- שונות במקבץ בגלל דגימה אקראית של דוגמאות ממערך האימון לכל מקבץ.
- קבוצות קטנות של נתונים לאימות
- שימוש בקצב למידה גבוה מדי בשלב מאוחר באימון.
פתרונות אפשריים:
- הגדלת גודל האצווה.
- קבלת נתוני אימות נוספים.
- שימוש בדעיכה של קצב הלמידה.
- שימוש בשיטת הממוצע של פוליאק.
האם עדיין יש שיפורים בניסויים בסוף ההכשרה? אם כן, אתם נמצאים במצב 'מוגבל על ידי חישוב' ויכול להיות שתפיקו תועלת מהגדלת מספר שלבי האימון או משינוי לוח הזמנים של קצב הלמידה.
האם הביצועים במערכי האימון והאימות הגיעו לנקודת רוויה הרבה לפני שלב האימון הסופי? אם כן, זה מצביע על כך שאתם נמצאים במצב 'לא מוגבל על ידי מחשוב', ואולי תוכלו להקטין את מספר שלבי האימון.
מעבר לרשימה הזו, אפשר לראות הרבה התנהגויות נוספות בגרפים של הפסדי האימון. לדוגמה, אם ההפסד של האימון עולה במהלך האימון, בדרך כלל זה מצביע על באג בצינור העיבוד של האימון.
זיהוי שינוי שימושי באמצעות תרשימי בידוד
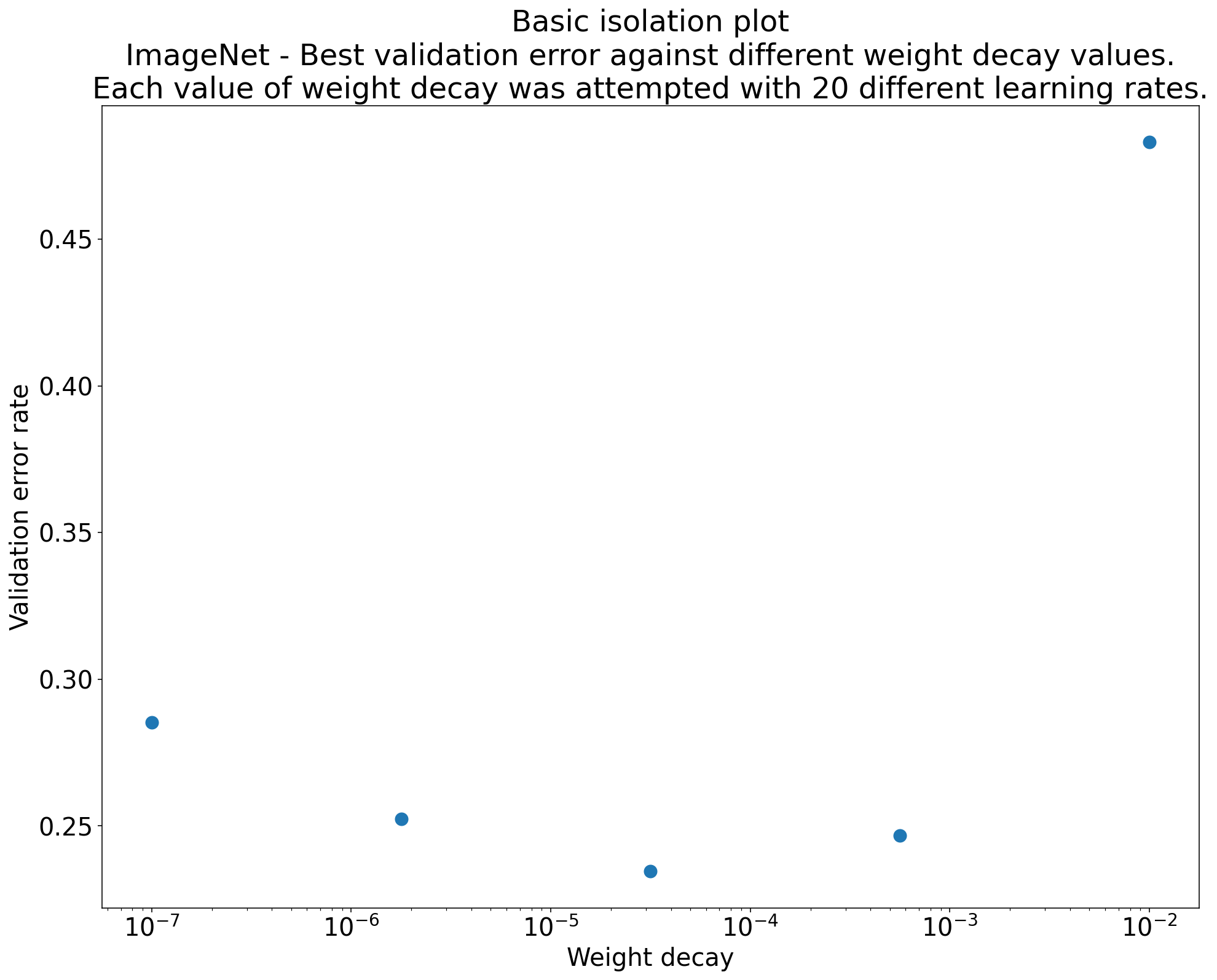
איור 2: תרשים בידוד שבודק את הערך הטוב ביותר של דעיכת המשקל עבור ResNet-50 שאומן על ImageNet.
לרוב, המטרה של סדרת ניסויים היא להשוות בין ערכים שונים של היפרפרמטר מדעי. לדוגמה, נניח שאתם רוצים לקבוע את ערך דעיכת המשקל שמניב את שגיאת האימות הטובה ביותר. גרף בידוד הוא מקרה מיוחד של גרף ציר היפרפרמטר בסיסי. כל נקודה בתרשים הבידוד מתאימה לביצועים של הניסוי הכי טוב בחלק מההיפרפרמטרים המפריעים (או בכולם). במילים אחרות, צריך לשרטט את ביצועי המודל אחרי 'אופטימיזציה' של הפרמטרים העודפים.
תרשים בידוד מפשט את ההשוואה בין ערכים שונים של ההיפרפרמטר המדעי. לדוגמה, בעלילה של הבידוד באיור 2 אפשר לראות את הערך של דעיכת המשקל שמניב את ביצועי האימות הטובים ביותר עבור הגדרה מסוימת של ResNet-50 שאומן על ImageNet.
אם המטרה היא להחליט אם לכלול דעיכת משקל בכלל, צריך להשוות את הנקודה הכי טובה מהתרשים הזה לנקודת הבסיס של אי-דעיכת משקל. כדי שההשוואה תהיה הוגנת, צריך לכוון את קצב הלמידה של נקודת הבסיס באותה מידה.
אם יש לכם נתונים שנוצרו על ידי חיפוש (כמעט) אקראי ואתם שוקלים להשתמש בהיפרפרמטר רציף לתרשים בידוד, אתם יכולים ליצור קירוב לתרשים הבידוד על ידי חלוקת ערכי ציר ה-x של תרשים ציר ההיפרפרמטר הבסיסי לקטגוריות, ובחירת הניסיון הטוב ביותר בכל פרוסת נתונים אנכית שמוגדרת על ידי הקטגוריות.
אוטומציה של תרשימים שימושיים באופן כללי
ככל שנדרש יותר מאמץ כדי ליצור תרשימים, כך פחות סביר שתעיינו בהם כמו שצריך. לכן, מומלץ להגדיר את התשתית כך שתפיק כמה שיותר תרשימים באופן אוטומטי. לפחות, מומלץ ליצור באופן אוטומטי תרשימי צירים של היפרפרמטרים בסיסיים לכל ההיפרפרמטרים שמשתנים בניסוי.
בנוסף, מומלץ ליצור באופן אוטומטי עקומות הפסד לכל הניסויים. בנוסף, מומלץ להקל ככל האפשר על מציאת כמה מהניסויים הטובים ביותר בכל מחקר ועל בחינת עקומות ההפסד שלהם.
אפשר להוסיף עוד הרבה תרשימים ורכיבים חזותיים שימושיים. פרפרזה של ג'פרי הינטון:
בכל פעם שאתם מתכננים משהו חדש, אתם לומדים משהו חדש.
החלטה אם לאמץ את השינוי המוצע
סיכום: כשמחליטים אם לבצע שינוי במודל או בהליך ההדרכה, או לאמץ הגדרה חדשה של היפרפרמטרים, חשוב לשים לב למקורות השונות השונים בתוצאות.
כשמנסים לשפר מודל, יכול להיות ששינוי מסוים יניב שגיאת אימות טובה יותר בהשוואה להגדרה הקיימת. עם זאת, יכול להיות שחזרה על הניסוי לא תראה יתרון עקבי. באופן לא רשמי, אפשר לקבץ את המקורות הכי חשובים לתוצאות לא עקביות לקטגוריות הרחבות הבאות:
- שונות בהליך ההכשרה, שונות בהכשרה מחדש או שונות בניסוי: השונות בין הרצות של הכשרה שמשתמשות באותם היפרפרמטרים אבל בערכי התחלה אקראיים שונים. לדוגמה, אתחולים אקראיים שונים, ערבובים של נתוני אימון, מסכות של נשירה, דפוסים של פעולות הגדלת נתונים וסדר של פעולות אריתמטיות מקבילות הם כולם מקורות פוטנציאליים לשונות בניסוי.
- שונות בחיפוש היפרפרמטרים או שונות במחקר: השונות בתוצאות שנובעת מההליך שלנו לבחירת ההיפרפרמטרים. לדוגמה, יכול להיות שתריצו את אותו הניסוי עם מרחב חיפוש מסוים, אבל עם שני ערכי seed שונים לחיפוש פסאודו-אקראי, ובסופו של דבר תבחרו ערכים שונים של היפרפרמטרים.
- שונות של איסוף נתונים ודגימה: השונות מכל סוג של פיצול אקראי לנתוני אימון, אימות ובדיקה, או שונות שנובעת מתהליך יצירת נתוני האימון באופן כללי יותר.
נכון, אפשר להשוות שיעורי שגיאות אימות שמוערכים על קבוצת אימות סופית באמצעות בדיקות סטטיסטיות קפדניות. עם זאת, לעיתים השונות של הניסוי לבדה יכולה להפיק הבדלים בעלי מובהקות סטטיסטית בין שני מודלים מאומנים שונים שמשתמשים באותן הגדרות של היפרפרמטרים.
הדבר שהכי חשוב לנו הוא השונות במחקר כשמנסים להסיק מסקנות שחורגות מהרמה של נקודה ספציפית במרחב של היפרפרמטרים. השונות במחקר תלויה במספר הניסויים ובמרחב החיפוש. ראינו מקרים שבהם השונות של המחקר גדולה יותר מהשונות של תקופת הניסיון, ומקרים שבהם היא קטנה בהרבה. לכן, לפני שמיישמים שינוי מומלץ, כדאי להריץ את הניסוי הטוב ביותר N פעמים כדי לאפיין את השונות בין הניסויים. בדרך כלל, אפשר להסתפק בסיווג מחדש של השונות בניסוי אחרי שינויים משמעותיים בצינור, אבל במקרים מסוימים יכול להיות שתצטרכו הערכות עדכניות יותר. באפליקציות אחרות, העלות של אפיון השונות בניסוי גבוהה מדי.
אמנם אתם רוצים לאמץ רק שינויים (כולל הגדרות חדשות של היפרפרמטרים) שמניבים שיפורים אמיתיים, אבל גם לא נכון לדרוש ודאות מוחלטת ששינוי מסוים עוזר. לכן, אם נקודה חדשה של היפרפרמטר (או שינוי אחר) מניבה תוצאה טובה יותר מהתוצאה של נקודת הבסיס (בהתחשב בשונות של האימון מחדש של הנקודה החדשה ושל נקודת הבסיס, ככל האפשר), כדאי לאמץ אותה כנקודת הבסיס החדשה להשוואות עתידיות. עם זאת, אנחנו ממליצים לאמץ רק שינויים שמניבים שיפורים שגדולים יותר מכל מורכבות שהם מוסיפים.
אחרי שהחיפוש מסתיים
סיכום: כדאי להשתמש בכלים של אופטימיזציה בייסיאנית אחרי שמסיימים לחפש מרחבי חיפוש טובים ומחליטים אילו היפרפרמטרים כדאי לכוונן.
בסופו של דבר, סדר העדיפויות שלכם ישתנה. במקום ללמוד עוד על בעיית ההתאמה, תרצו ליצור את ההגדרה הטובה ביותר להפעלה או לשימוש אחר. בשלב הזה, אמור להיות מרחב חיפוש משופר שמכיל בנוחות את האזור המקומי סביב הניסוי הטוב ביותר שנצפה, ושנדגם בצורה מספקת. תהליך האופטימיזציה אמור לחשוף את ההיפרפרמטרים החיוניים ביותר שצריך לשנות ואת הטווחים הסבירים שלהם. תוכלו להשתמש בטווחים האלה כדי ליצור מרחב חיפוש למחקר סופי של אופטימיזציה אוטומטית, תוך שימוש בתקציב אופטימיזציה גדול ככל האפשר.
מכיוון שכבר לא חשוב לך למקסם את התובנות לגבי בעיית ההתאמה, הרבה מהיתרונות של חיפוש פסאודו-אקראי כבר לא רלוונטיים. לכן, כדאי להשתמש בכלי אופטימיזציה בייסיאנית כדי למצוא באופן אוטומטי את ההגדרה הטובה ביותר של היפרפרמטרים. Open-Source Vizier מיישם מגוון אלגוריתמים מתוחכמים לכוונון מודלים של למידת מכונה, כולל אלגוריתמים של אופטימיזציה בייסיאנית.
נניח שמרחב החיפוש מכיל נפח לא טריוויאלי של נקודות שונות, כלומר נקודות שמקבלות הפסד אימון מסוג NaN או אפילו הפסד אימון שגרוע מהממוצע בהרבה סטיות תקן. במקרה כזה, מומלץ להשתמש בכלים לאופטימיזציה של קופסה שחורה שמטפלים בצורה נכונה בניסויים שמתפצלים. (במאמר אופטימיזציה בייסיאנית עם אילוצים לא ידועים מוסבר על דרך מצוינת לפתור את הבעיה הזו). ל-Vizier בקוד פתוח יש תמיכה בסימון נקודות שונות על ידי סימון ניסויים כלא מעשיים, אבל יכול להיות שהוא לא ישתמש בגישה המועדפת שלנו מתוך Gelbart et al., בהתאם לאופן ההגדרה שלו.
אחרי שהתהליך מסתיים, כדאי לבדוק את הביצועים במערך הבדיקה. באופן עקרוני, אפשר אפילו לכלול את קבוצת האימות בקבוצת האימון ולאמן מחדש את ההגדרה הטובה ביותר שנמצאה באמצעות אופטימיזציה בייסיאנית. עם זאת, זה מתאים רק אם לא יהיו השקות עתידיות עם עומס העבודה הספציפי הזה (למשל, תחרות חד-פעמית ב-Kaggle).
