Uma abordagem científica para melhorar o desempenho do modelo

Para os fins deste documento:

O objetivo final do desenvolvimento de machine learning é maximizar a utilidade do modelo implantado.

Normalmente, é possível usar os mesmos princípios e etapas básicas nesta seção sobre qualquer problema de ML.

Esta seção parte dos seguintes pressupostos:

• Você já tem um pipeline de treinamento em execução, junto com uma configuração que recebe um resultado razoável.
• Você tem recursos computacionais suficientes para realizar experimentos de ajuste significativos e executar pelo menos vários jobs de treinamento em paralelo.

A estratégia de ajuste incremental

Recomendação: comece com uma configuração simples. Em seguida, faça melhorias de modo incremental, criando insights sobre o problema. Certifique-se de que qualquer melhoria seja baseada em evidências fortes.

Presumimos que seu objetivo seja encontrar uma configuração que maximize o desempenho do seu modelo. Às vezes, sua meta é maximizar a melhoria do modelo por um prazo fixo. Em outros casos, é possível continuar melhorando o modelo indefinidamente. Por exemplo, aprimorando continuamente um modelo usado na produção.

Em princípio, você poderia maximizar o desempenho usando um algoritmo para pesquisar automaticamente todo o espaço de configurações possíveis, mas essa não é uma opção prática. O espaço de possíveis configurações é extremamente grande e ainda não há algoritmos sofisticados o suficiente para pesquisar com eficiência esse espaço sem orientação humana. A maioria dos algoritmos de pesquisa automatizada conta com um espaço de pesquisa projetado manualmente que define o conjunto de configurações a ser pesquisado. Esses espaços de pesquisa podem ser importantes.

A maneira mais eficiente de maximizar o desempenho é começar com uma configuração simples e adicionar recursos e fazer melhorias de maneira incremental, enquanto desenvolve insights sobre o problema.

Recomendamos o uso de algoritmos de pesquisa automatizados em cada rodada de ajuste e atualização contínua de espaços de pesquisa à medida que sua compreensão aumenta. À medida que explora, você encontrará configurações cada vez melhores e, portanto, seu "melhor" modelo será continuamente aprimorado.

O termo "lançamento" se refere a uma atualização da nossa melhor configuração, que pode ou não corresponder a um lançamento real de um modelo de produção. Para cada "lançamento", você precisa garantir que a alteração seja baseada em fortes evidências, e não apenas na probabilidade aleatória com base em uma configuração de sorte. Assim, você não adiciona complexidade desnecessária ao pipeline de treinamento.

Em um alto nível, nossa estratégia de ajuste incremental envolve a repetição das quatro etapas a seguir:

1. Escolha uma meta para a próxima rodada de experimentos. Verifique se o escopo da meta está definido corretamente.
2. Criar a próxima rodada de experimentos. Elabore e execute um conjunto de experiências que progrida em relação a essa meta.
3. Aprenda com os resultados experimentais. Avalie o experimento em relação a uma lista de verificação.
4. Determine se você quer adotar a alteração do candidato.

O restante desta seção detalha essa estratégia.

Escolha uma meta para a próxima rodada de experiências

Se você tentar adicionar vários recursos ou responder a várias perguntas de uma só vez, talvez não seja possível desfazer os efeitos separados nos resultados. Exemplos de metas incluem:

• Tente uma possível melhoria no pipeline (por exemplo, um novo regularizador, escolha de pré-processamento etc.).
• Entender o impacto de um hiperparâmetro de modelo específico (por exemplo, a função de ativação)
• Minimize o erro de validação.

Priorize o progresso a longo prazo em vez de melhorar os erros de validação de curto prazo

Resumo: na maioria das vezes, sua meta principal é conseguir informações sobre o problema de ajuste.

Recomendamos que a maior parte do tempo você receba insights sobre o problema e, em comparação, pouco tempo se concentra em maximizar o desempenho no conjunto de validação. Em outras palavras, gaste a maior parte do tempo em "exploração" e apenas uma pequena quantidade de "exploração". Entender o problema é fundamental para maximizar o desempenho final. Priorizar insights sobre ganhos de curto prazo ajuda a:

• Evite lançar alterações desnecessárias em execuções com bom desempenho apenas por acidente histórico.
• Identifique quais hiperparâmetros são mais sensíveis ao erro de validação, quais são os que mais interagem e, portanto, precisam ser ajustados juntos. Eles também são insensíveis a outras alterações e, portanto, podem ser corrigidos em experimentos futuros.
• Sugira novos recursos em potencial para testar, como novos regularizadores quando o overfitting for um problema.
• Identifique os recursos que não ajudam e, portanto, podem ser removidos, reduzindo a complexidade dos experimentos futuros.
• Reconhecer quando as melhorias do ajuste de hiperparâmetro provavelmente foram saturadas.
• Restrinja nossos espaços de pesquisa com base no valor ideal para melhorar a eficiência do ajuste.

Futuramente, você entenderá o problema. Assim, é possível se concentrar somente no erro de validação, mesmo que os experimentos não sejam maximicamente informativos sobre a estrutura do problema de ajuste.

Criar a próxima rodada de experimentos

Resumo: identifique quais hiperparâmetros são científicos, de incômodo e fixos para a meta experimental. Crie uma sequência de estudos para comparar valores diferentes dos hiperparâmetros científicos e otimizar os hiperparâmetros incômodos. Escolha o espaço de pesquisa de hiperparâmetros incômodos para equilibrar os custos dos recursos com o valor científico.

Identificar hiperparâmetros científicos, de incômodo e fixos

Para uma determinada meta, todos os hiperparâmetros se enquadram em uma das seguintes categorias:

• Os hiperparâmetros científicos são aqueles com efeito sobre o desempenho do modelo que você está tentando medir.
• Os hiperparâmetros incômodos são aqueles que precisam ser otimizados para comparar valores diferentes dos hiperparâmetros científicos. Os hiperparâmetros de incômodo são semelhantes aos parâmetros de incômodo nas estatísticas.
• Os hiperparâmetros fixos têm valores constantes na rodada atual de experimentos. Os valores de hiperparâmetros fixos não devem ser alterados quando você comparar valores diferentes de hiperparâmetros científicos. Ao corrigir determinados hiperparâmetros para um conjunto de experimentos, você precisa aceitar que as conclusões derivadas dos experimentos podem não ser válidas para outras configurações dos hiperparâmetros fixos. Em outras palavras, os hiperparâmetros fixos criam ressalvas para todas as conclusões que você tira dos experimentos.

Por exemplo, suponha que sua meta seja a seguinte:

Determinar se um modelo com mais camadas ocultas tem menor erro de validação.

Neste caso:

• A taxa de aprendizado é um hiperparâmetro incômodo porque só é possível comparar modelos de maneira justa com diferentes números de camadas escondidas se ela for ajustada separadamente para cada um. A taxa de aprendizado ideal geralmente depende da arquitetura do modelo.
• A função de ativação pode ser um hiperparâmetro fixo se você tiver determinado em experimentos anteriores que a melhor função de ativação não é sensível à profundidade do modelo. Ou você está disposto a limitar suas conclusões sobre o número de camadas escondidas para cobrir essa função de ativação. Como alternativa, ele pode ser um hiperparâmetro incômodo se você estiver preparado para ajustá-lo separadamente para cada número de camadas escondidas.

Um hiperparâmetro específico pode ser um hiperparâmetro científico, de incômodo ou fixo. A designação do hiperparâmetro muda de acordo com a meta experimental. Por exemplo, a função de ativação pode ser qualquer uma das seguintes:

• hiperparâmetro científico: o ReLU ou o tanh são uma opção melhor para nosso problema?
• hiperparâmetro incômodo: o melhor modelo de cinco camadas é melhor que o melhor modelo de seis camadas quando você permite várias funções de ativação possíveis?
• hiperparâmetro corrigido: para redes ReLU, adicionar normalização em lote em uma posição específica ajuda?

Ao criar uma nova rodada de experiências:

1. Identifique os hiperparâmetros científicos do objetivo experimental. Nesse estágio, considere todos os outros hiperparâmetros como hiperparâmetros incômodos.
2. Converta alguns hiperparâmetros incômodos em hiperparâmetros fixos.

Com recursos ilimitados, você deixaria todos os hiperparâmetros não científicos como hiperparâmetros incômodos, para que as conclusões obtidas dos seus experimentos estivessem livres de ressalvas sobre valores fixos de hiperparâmetros. No entanto, quanto mais hiperparâmetros incômodos você tentar ajustar, maior será o risco de não ajustá-los o suficiente para cada configuração dos hiperparâmetros científicos e acabar chegando às conclusões erradas dos seus experimentos. Conforme descrito em uma seção posterior, você pode evitar esse risco aumentando o orçamento computacional. No entanto, seu orçamento máximo de recursos geralmente é menor do que o necessário para ajustar todos os hiperparâmetros não científicos.

Recomendamos converter um hiperparâmetro incômodo em um hiperparâmetro fixo quando as ressalvas introduzidas pela correção forem menos onerosas do que o custo de incluí-lo como um hiperparâmetro incômodo. Quanto mais um hiperparâmetro incômodo interagir com os hiperparâmetros científicos, mais danos serão necessários para corrigir esse valor. Por exemplo, o melhor valor da força da redução de peso normalmente depende do tamanho do modelo. Portanto, comparar diferentes tamanhos de modelo, supondo que um único valor específico da redução de peso não seria muito relevante.

Alguns parâmetros do otimizador

Como regra geral, alguns hiperparâmetros do otimizador (por exemplo, taxa de aprendizado, momento, parâmetros de programação de taxa de aprendizado, versões Beta do Adam etc.) são hiperparâmetros incômodos, porque tendem a interagir mais com outras mudanças. Esses hiperparâmetros do otimizador raramente são científicos, porque uma meta como "qual é a melhor taxa de aprendizado para o pipeline atual?" não fornece muitos insights. Afinal, a melhor configuração pode mudar com a próxima alteração do pipeline.

Alguns hiperparâmetros do otimizador podem ser corrigidos ocasionalmente devido a restrições de recursos ou a evidências particularmente fortes de que eles não interagem com os parâmetros científicos. No entanto, geralmente é necessário presumir que é preciso ajustar os hiperparâmetros do otimizador separadamente para fazer comparações justas entre diferentes configurações dos hiperparâmetros científicos. Portanto, não é necessário corrigi-los. Além disso, não há um motivo prioritário para preferir um valor de hiperparâmetro do otimizador a outro. Por exemplo, os valores de hiperparâmetro do otimizador geralmente não afetam o custo computacional de passes ou gradientes futuros.

A escolha do otimizador

A escolha do otimizador normalmente é:

• um hiperparâmetro científico
• um hiperparâmetro fixo

Um otimizador é um hiperparâmetro científico se seu objetivo experimental envolve fazer comparações justas entre dois ou mais otimizadores diferentes. Por exemplo:

Determine qual otimizador produz o menor erro de validação em um determinado número de etapas.

Como alternativa, é possível tornar o otimizador um hiperparâmetro fixo por vários motivos, incluindo:

• Experimentos anteriores sugerem que o melhor otimizador para seu problema de ajuste não é sensível aos hiperparâmetros científicos atuais.
• Você prefere comparar valores de hiperparâmetros científicos usando esse otimizador, porque as curvas de treinamento são mais fáceis de entender.
• Você prefere usar esse otimizador porque ele usa menos memória do que as alternativas.

hiperparâmetros de regularização

Os hiperparâmetros introduzidos por uma técnica de regularização geralmente são hiperparâmetros incômodos. No entanto, a escolha de incluir ou não a técnica de regularização é um hiperparâmetro científico ou fixo.

Por exemplo, a regularização de dropout adiciona complexidade de código. Portanto, ao decidir incluir ou não a regularização de dropout, é possível fazer com que "sem dropout" e "desistência" sejam um hiperparâmetro científico, mas a taxa de dropout seja um hiperparâmetro incômodo. Se você decidir adicionar a regularização de dropout ao pipeline com base nesse experimento, a taxa de desistência seria um hiperparâmetro incômodo em experimentos futuros.

Hiperparâmetros arquitetônicos

Os hiperparâmetros de arquitetura geralmente são científicos ou fixos, porque as mudanças na arquitetura podem afetar os custos de disponibilização e treinamento, a latência e os requisitos de memória. Por exemplo, o número de camadas geralmente é um hiperparâmetro científico ou fixo, já que tende a ter consequências drásticas para o treinamento e o uso de memória.

Dependências de hiperparâmetros científicos

Em alguns casos, os conjuntos de incômodos e hiperparâmetros fixos dependem dos valores dos hiperparâmetros científicos. Por exemplo, suponha que você esteja tentando determinar qual otimizador no momentoro de Nesserov e Adam produz o menor erro de validação. Neste caso:

• O hiperparâmetro científico é o otimizador, que usa valores {"Nesterov_momentum", "Adam"}
• O valor optimizer="Nesterov_momentum" introduz os hiperparâmetros {learning_rate, momentum}, que podem ser inconvenientes ou hiperparâmetros fixos.
• O valor optimizer="Adam" introduz os hiperparâmetros {learning_rate, beta1, beta2, epsilon}, que podem ser hiperparâmetros incômodos ou fixos.

Os hiperparâmetros presentes apenas em determinados valores dos hiperparâmetros científicos são chamados de hiperparâmetros condicionais. Não presuma que dois hiperparâmetros condicionais são iguais por terem o mesmo nome. No exemplo anterior, o hiperparâmetro condicional chamado learning_rate é diferente de optimizer="Nesterov_momentum" para optimizer="Adam". Seu papel é semelhante (embora não seja idêntico) nos dois algoritmos, mas o intervalo de valores que funciona bem em cada um dos otimizadores normalmente é diferente por várias ordens de magnitude.

Criar um conjunto de estudos

Depois de identificar os hiperparâmetros científicos e incômodos, projete um estudo ou sequência de estudos para progredir em direção ao objetivo experimental. Um estudo especifica um conjunto de configurações de hiperparâmetros que serão executados para análise posterior. Cada configuração é chamada de teste. A criação de um estudo geralmente envolve escolher o seguinte:

• Os hiperparâmetros que variam entre os testes.
• Os valores que os hiperparâmetros podem assumir (o espaço de pesquisa).
• O número de tentativas.
• Um algoritmo de pesquisa automatizado para amostragem de tantos testes do espaço de pesquisa.

Como alternativa, crie um estudo especificando o conjunto de configurações de hiperparâmetro manualmente.

O objetivo dos estudos é:

• Execute o canal com valores diferentes dos hiperparâmetros científicos.
• "Otimizar" (ou otimizar) os hiperparâmetros incômodos para que as comparações entre valores diferentes dos hiperparâmetros científicos sejam o mais justas possível.

No caso mais simples, você faria um estudo separado para cada configuração dos parâmetros científicos, em que cada estudo ajusta os hiperparâmetros incômodos. Por exemplo, se o seu objetivo é selecionar o melhor otimizador do momento "Nestrov" e do Adam, você pode criar dois estudos:

• Um estudo em que optimizer="Nesterov_momentum" e os hiperparâmetros incômodos são {learning_rate, momentum}
• Outro estudo em que optimizer="Adam" e os hiperparâmetros incômodos são {learning_rate, beta1, beta2, epsilon}.

Você compararia os dois otimizadores selecionando o teste de melhor desempenho de cada estudo.

Você pode usar qualquer algoritmo de otimização sem gradiente, incluindo métodos como otimização bayesiana ou algoritmos evolutivos, para otimizar os hiperparâmetros incômodos. No entanto, preferimos usar a pesquisa semialeatória na fase de exploração do ajuste devido a várias vantagens nessa configuração. Após a conclusão da exploração, recomendamos usar um software de otimização bayesiano de última geração (se disponível).

Considere um caso mais complicado em que você queira comparar um grande número de valores dos hiperparâmetros científicos, mas não é prático fazer tantos estudos independentes. Nesse caso, você pode fazer o seguinte:

• Inclua os parâmetros científicos no mesmo espaço de pesquisa que os hiperparâmetros incômodos.
• Usar um algoritmo de pesquisa para coletar amostras de valores dos hiperparâmetros científicos e de incômodo em um único estudo.

Ao adotar essa abordagem, os hiperparâmetros condicionais podem causar problemas. Afinal, é difícil especificar um espaço de pesquisa, a menos que o conjunto de hiperparâmetros incômodos seja o mesmo para todos os valores dos hiperparâmetros científicos. Nesse caso, nossa preferência por usar a pesquisa quase aleatória em vez de ferramentas de otimização de caixa preta mais avançadas é ainda mais forte, já que garante que diferentes valores dos hiperparâmetros científicos serão amostrados de maneira uniforme. Independentemente do algoritmo de pesquisa, verifique se ele pesquisa os parâmetros científicos de maneira uniforme.

Encontre o equilíbrio entre experiências informativas e acessíveis

Ao criar um estudo ou uma sequência de estudos, aloque um orçamento limitado para atingir adequadamente as três metas a seguir:

• Comparação de valores diferentes o suficiente dos hiperparâmetros científicos.
• Ajustar os hiperparâmetros incômodos em um espaço de pesquisa grande o suficiente.
• Amostragem do espaço de pesquisa de hiperparâmetros incômodos o suficiente.

Quanto mais você conseguir alcançar essas três metas, mais insights poderá extrair do experimento. Comparar o maior número possível de hiperparâmetros científicos amplia o escopo dos insights obtidos com o experimento.

Incluir o maior número possível de hiperparâmetros incômodos e permitir que cada hiperparâmetro varie para o maior intervalo possível aumenta a confiança de que um valor "bom" dos hiperparâmetros incômodos existe no espaço de pesquisa para cada configuração dos hiperparâmetros científicos. Caso contrário, é possível fazer comparações injustas entre os valores dos hiperparâmetros científicos, não pesquisando regiões possíveis do espaço de hiperparâmetros incômodos em que valores melhores possam estar para alguns valores dos parâmetros científicos.

Amostra do espaço de pesquisa de hiperparâmetros incômodos o mais densamente possível. Isso aumenta a confiança de que o procedimento de pesquisa encontrará todas as configurações adequadas para os hiperparâmetros incômodos que existem no seu espaço de pesquisa. Caso contrário, é possível fazer comparações injustas entre os valores dos parâmetros científicos, porque alguns deles estão com sorte de fazer a amostragem dos hiperparâmetros incômodos.

Infelizmente, as melhorias em qualquer uma dessas três dimensões exigem uma destas opções:

• Aumentar o número de testes e, portanto, o custo do recurso.
• Encontrar uma maneira de salvar recursos em uma das outras dimensões.

Cada problema tem as próprias idiossincrasias e restrições computacionais. Portanto, alocar recursos nesses três objetivos requer algum nível de conhecimento do domínio. Depois de executar um estudo, sempre tente saber se o estudo ajustou os hiperparâmetros incômodos o suficiente. Ou seja, o estudo pesquisou um espaço grande o suficiente para comparar de forma justa os hiperparâmetros científicos (conforme descrito em mais detalhes na próxima seção).

Aprenda com os resultados experimentais

Recomendação: além de tentar atingir a meta científica original de cada grupo de experimentos, siga a lista de verificação de perguntas adicionais. Se você descobrir problemas, revise e execute novamente os experimentos.

Em última análise, cada grupo de experiências tem uma meta específica. Avalie as evidências que os experimentos oferecem em relação a esse objetivo. No entanto, se você fizer as perguntas certas, geralmente poderá encontrar problemas para corrigir antes que um determinado conjunto de experimentos atinja a meta original. Se você não fizer essas perguntas, poderá tirar conclusões incorretas.

Como a execução de experimentos pode ser cara, você também precisa extrair outros insights úteis de cada grupo de experiências, mesmo que esses insights não sejam imediatamente relevantes para a meta atual.

Antes de analisar um determinado conjunto de experiências para progredir em direção à meta original, pergunte-se o seguinte:

• O espaço de pesquisa é grande o suficiente? Se o ponto ideal de um estudo estiver perto do limite do espaço de pesquisa em uma ou mais dimensões, a pesquisa provavelmente não será grande o suficiente. Nesse caso, faça outro estudo com um espaço de pesquisa expandido.
• Você já conseguiu uma quantidade suficiente de pontos do espaço de pesquisa? Caso contrário, execute mais pontos ou menos ambicioso nas metas de ajuste.
• Qual fração dos testes em cada estudo é inviável? Ou seja, quais testes divergem, recebem valores de perda muito ruins ou falham na execução porque violam alguma restrição implícita? Quando uma fração de pontos muito grande em um estudo for inviável, ajuste o espaço de pesquisa para evitar a amostragem desses pontos, o que, às vezes, requer a reparação do espaço de pesquisa. Em alguns casos, um grande número de pontos inviáveis pode indicar um bug no código de treinamento.
• O modelo apresenta problemas de otimização?
• O que você pode aprender com as curvas de treinamento dos melhores testes? Por exemplo, as melhores avaliações têm curvas de treinamento consistentes com overfitting problemático?

Se necessário, com base nas respostas às perguntas anteriores, refine o estudo mais recente ou o grupo de estudos para melhorar o espaço de pesquisa e/ou coletar mais amostras ou faça outras ações corretivas.

Depois de responder às perguntas anteriores, avalie as evidências que as experiências fornecem em relação à sua meta original, por exemplo, avaliar se uma alteração é útil.

Identificar limites inadequados de espaço de pesquisa

Um espaço de pesquisa é suspeito se o melhor ponto de amostragem dele está perto do limite. Talvez você encontre um ponto ainda melhor se expandir o intervalo de pesquisa nessa direção.

Para verificar os limites do espaço de pesquisa, recomendamos traçar testes concluídos no que chamamos de gráficos básicos do eixo de hiperparâmetros. Neles, traçamos o valor do objetivo de validação em relação a um dos hiperparâmetros (por exemplo, taxa de aprendizado). Cada ponto no gráfico corresponde a um único teste.

O valor do objetivo de validação para cada teste geralmente é o melhor valor alcançado ao longo do treinamento.

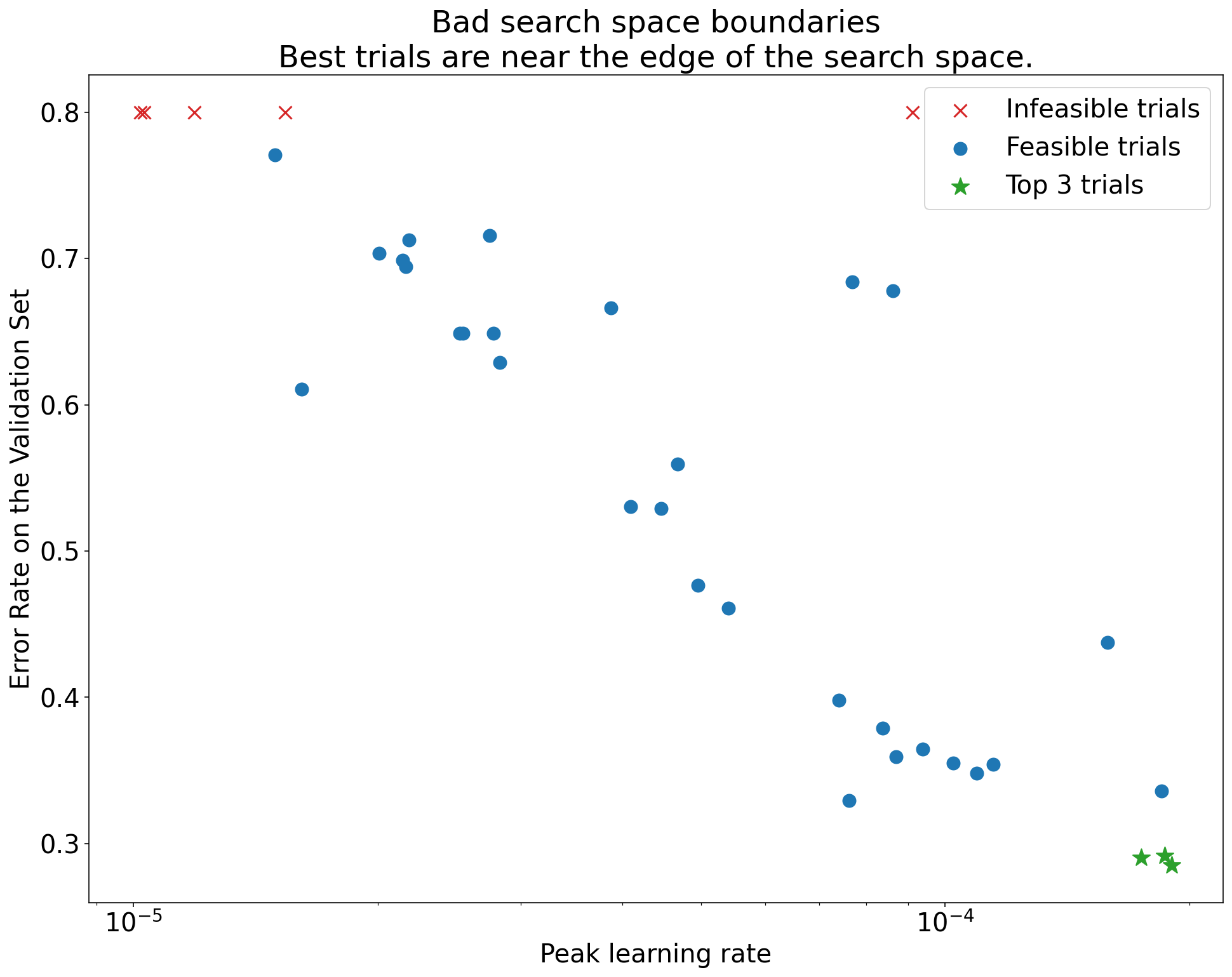
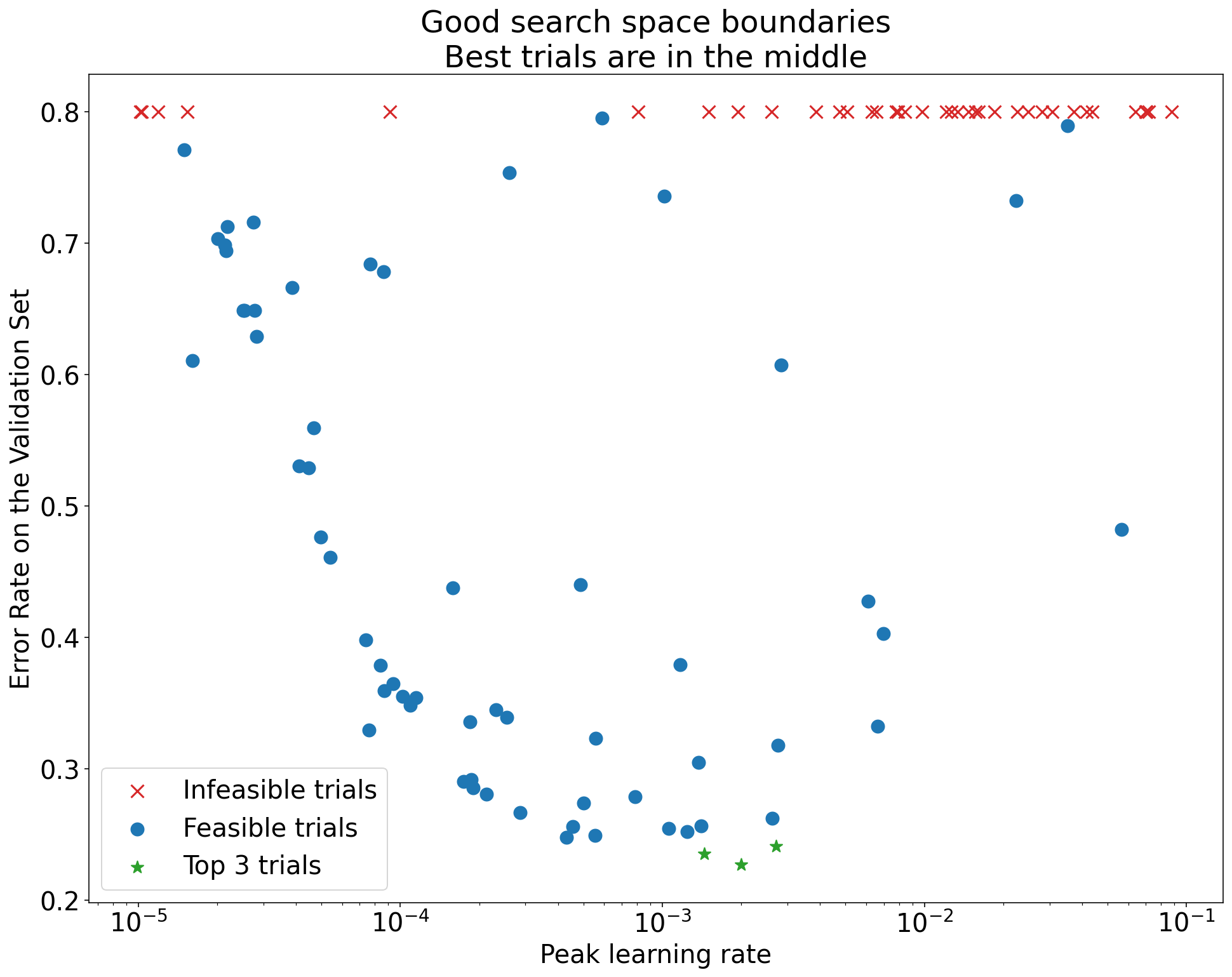
Figura 1: exemplos de limites de espaço de pesquisa inválidos e aceitáveis.

Os gráficos na Figura 1 mostram a taxa de erro (quanto mais baixo, melhor) do que a taxa de aprendizado inicial. Se os melhores pontos se agrupam em direção à borda de um espaço de pesquisa (em alguma dimensão), talvez seja necessário expandir os limites do espaço de pesquisa até que o melhor ponto observado não esteja mais perto do limite.

Muitas vezes, um estudo inclui testes "inviáveis" que divergem ou recebem resultados muito ruins (marcados com "Xs" vermelhos na Figura 1). Se todos os testes forem inviáveis para taxas de aprendizado maiores que um valor de limite e se os testes com melhor desempenho tiverem taxas de aprendizado na extremidade dessa região, o modelo pode ter problemas de estabilidade que o impedem de acessar taxas de aprendizado mais altas.

Não há amostragem de pontos suficientes no espaço de pesquisa

Em geral, pode ser muito difícil saber se a amostragem do espaço de pesquisa foi densa o suficiente. 🤖 Executar mais testes é melhor do que realizar menos testes. No entanto, mais testes geram um custo extra óbvio.

Como é muito difícil saber quando você tem amostras suficientes, recomendamos:

• Amostras do que você pode pagar.
• Calibrar sua confiança intuitiva de observar repetidamente vários gráficos de eixo de hiperparâmetro e tentar ter uma noção de quantos pontos estão na região "boa" do espaço de pesquisa.

Examine as curvas de treinamento

Resumo: o exame das curvas de perda é uma maneira fácil de identificar modos de falha comuns e pode ajudar você a priorizar possíveis próximas ações.

Em muitos casos, o objetivo principal dos experimentos exige apenas considerar o erro de validação de cada teste. No entanto, tenha cuidado ao reduzir cada teste a um único número, porque esse foco pode ocultar detalhes importantes sobre o que está acontecendo abaixo da superfície. Para cada estudo, recomendamos que você analise as curvas de perda de pelo menos os melhores testes. Mesmo que isso não seja necessário para lidar com o objetivo experimental principal, examinar as curvas de perda (incluindo perda de treinamento e perda de validação) é uma boa maneira de identificar modos de falha comuns e pode ajudar você a priorizar quais ações serão tomadas em seguida.

Ao examinar as curvas de perda, concentre-se nas seguintes perguntas:

• Algum dos testes está com overfitting problemático? O overfitting problemático ocorre quando o erro de validação começa a aumentar durante o treinamento. Nas configurações experimentais em que você otimiza os hiperparâmetros incômodos selecionando o "melhor" teste para cada configuração dos hiperparâmetros científicos, verifique o overfitting problemático em pelo menos cada um dos melhores testes correspondentes às configurações dos hiperparâmetros que você está comparando. Se uma das melhores avaliações mostrar um overfitting problemático, siga um destes procedimentos ou ambos:

  • Executar o experimento novamente com outras técnicas de regularização
  • Ajuste novamente os parâmetros de regularização existentes antes de comparar os valores dos hiperparâmetros científicos. Isso não se aplica se os hiperparâmetros científicos incluírem parâmetros de regularização, já que não seria surpreendente se as configurações de baixa intensidade desses parâmetros resultassem em overfitting problemático.

  Reduzir o overfitting costuma ser simples usando técnicas de regularização comuns que adicionam complexidade de código mínima ou computação extra (por exemplo, regularização de dropout, suavização de rótulos, redução de peso). Portanto, normalmente é trivial adicionar um ou mais deles à próxima rodada de experiências. Por exemplo, se o hiperparâmetro científico for "número de camadas escondidas" e o melhor teste que usar o maior número de camadas ocultas exibir um overfitting problemático, recomendamos tentar novamente com regularização extra em vez de selecionar imediatamente o número menor de camadas escondidas.

  Mesmo que nenhum dos "melhores" testes exiba overfitting problemático, ainda pode haver um problema se ele ocorrer em qualquer um dos testes. A seleção do melhor teste suprime as configurações que exibem overfitting problemáticos e favorece aquelas que não o fazem. Em outras palavras, selecionar o melhor teste favorece as configurações com mais regularização. No entanto, qualquer coisa que torne o treinamento pior pode agir como um regularizador, mesmo que não tenha sido intencional. Por exemplo, a escolha de uma taxa de aprendizado menor pode regularizar o treinamento prejudicando o processo de otimização, mas normalmente não queremos escolher a taxa de aprendizado dessa maneira. O "melhor" teste para cada configuração de hiperparâmetros científicos pode ser selecionado de maneira a favorecer valores "ruins" de alguns deles.

• Há alta variação passo a passo no final do erro de treinamento ou de validação no treinamento? Em caso afirmativo, isso pode interferir no seguinte:

  • Sua capacidade de comparar valores diferentes dos hiperparâmetros científicos. Isso ocorre porque cada teste termina aleatoriamente em uma etapa "sortudo" ou "azar".
  • Sua capacidade de reproduzir o resultado do melhor teste em produção. Isso ocorre porque o modelo de produção pode não terminar na mesma etapa "sortudo" do estudo.

  As causas mais prováveis da variação passo a passo são:

  • Variação de lote devido à amostragem aleatória de exemplos do conjunto de treinamento para cada lote.
  • Pequenos conjuntos de validação
  • Usar uma taxa de aprendizado muito alta no treinamento.

  As possíveis soluções são:

  • Aumentar o tamanho do lote.
  • Coletando mais dados de validação.
  • Como usar o decaimento da taxa de aprendizado.
  • Usando a média do Polyak.

• Os testes ainda estão melhorando ao final do treinamento? Nesse caso, você está no regime de "computação limitada" e pode se beneficiar com o aumento do número de etapas de treinamento ou a alteração da programação da taxa de aprendizado.

• O desempenho nos conjuntos de treinamento e validação está saturado muito antes da etapa de treinamento final? Nesse caso, isso indica que você está no regime "sem limite de computação" e que pode diminuir o número de etapas de treinamento.

Além dessa lista, muitos comportamentos adicionais podem ficar evidentes ao examinar as curvas de perda. Por exemplo, o aumento da perda de treinamento durante o treinamento geralmente indica um bug no pipeline de treinamento.

Como detectar se uma alteração é útil com gráficos de isolamento

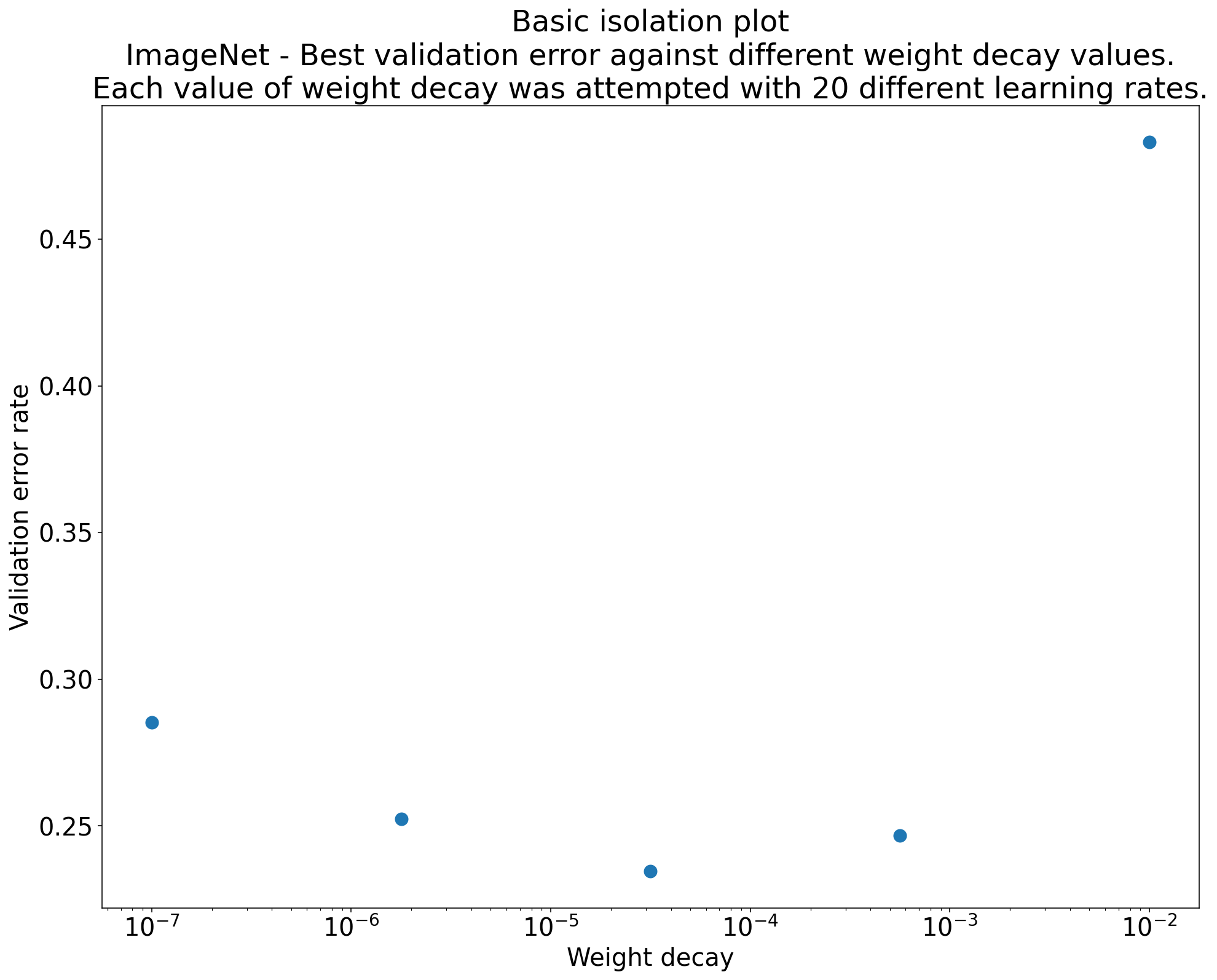
Figura 2: gráfico de isolamento que investiga o melhor valor de redução de peso para o ResNet-50 treinado no ImageNet.

 

Muitas vezes, o objetivo de um conjunto de experimentos é comparar diferentes valores de um hiperparâmetro científico. Por exemplo, suponha que você queira determinar o valor de redução de peso que resulta no melhor erro de validação. Um gráfico de isolamento é um caso especial do gráfico básico do eixo de hiperparâmetro. Cada ponto em um gráfico de isolamento corresponde ao desempenho do melhor teste em alguns (ou todos) os hiperparâmetros incômodos. Em outras palavras, plote o desempenho do modelo depois de "otimizar" os hiperparâmetros incômodos.

Um gráfico de isolamento simplifica a comparação entre diferentes valores do hiperparâmetro científico. Por exemplo, o gráfico de isolamento na Figura 2 revela o valor da redução de peso que produz o melhor desempenho de validação para uma configuração específica de ResNet-50 treinada no ImageNet.

Se o objetivo for determinar se deve incluir redução de peso, compare o melhor ponto desse gráfico com o valor de referência de nenhum decaimento. Para uma comparação justa, a linha de base também precisa ter a taxa de aprendizado igualmente bem ajustada.

Quando você tem dados gerados pela pesquisa (quase) aleatória e está considerando um hiperparâmetro contínuo para um gráfico de isolamento, é possível aproximar o gráfico de isolamento agrupando os valores do eixo x do gráfico de hiperparâmetro básico e fazendo o melhor teste em cada fatia vertical definida pelos buckets.

Automatize gráficos genéricos úteis

Quanto mais esforço for gerar os gráficos, menor será a probabilidade de vê-los o máximo possível. Portanto, recomendamos configurar sua infraestrutura para produzir automaticamente o máximo de gráficos possível. No mínimo, recomendamos gerar automaticamente gráficos de eixo de hiperparâmetros básicos para todos os hiperparâmetros que você varia em um experimento.

Além disso, recomendamos a produção automática de curvas de perda para todos os testes. Além disso, recomendamos facilitar ao máximo a localização dos melhores testes de cada estudo e examinar as curvas de perda.

É possível adicionar vários outros gráficos e visualizações úteis. Para parafrasear Geoffrey Hinton:

Toda vez que você cria algo novo, aprende algo novo.

Determinar se a alteração do candidato deve ser adotada

Resumo: ao decidir se você quer fazer uma alteração em nosso modelo ou procedimento de treinamento ou adotar uma nova configuração de hiperparâmetro, observe as diferentes fontes de variação nos resultados.

Ao tentar melhorar um modelo, uma alteração candidato específica pode inicialmente atingir um melhor erro de validação em comparação com uma configuração estabelecida. No entanto, repetir o experimento pode não demonstrar nenhuma vantagem consistente. As fontes mais importantes de resultados inconsistentes podem ser agrupadas nas seguintes categorias amplas:

• Variação de procedimento de treinamento, variação de treinamento ou variação de teste: a variação entre as execuções de treinamento que usam os mesmos hiperparâmetros, mas diferentes sugestões aleatórias. Por exemplo, inicializações aleatórias diferentes, embaralhamentos de dados de treinamento, máscaras de saída, padrões de operações de aumento de dados e ordens de operações aritméticas paralelas são possíveis fontes de variação de teste.
• Variação de pesquisa de hiperparâmetro ou variação de estudo: a variação nos resultados causada pelo procedimento para selecionar os hiperparâmetros. Por exemplo, você pode executar o mesmo experimento com um espaço de pesquisa específico, mas com duas sugestões diferentes para a pesquisa quase aleatória e acabar selecionando diferentes valores de hiperparâmetros.
• Variação da amostragem e coleta de dados: a variação de qualquer tipo de divisão aleatória em dados de treinamento, validação e teste ou variação devido ao processo de geração de dados de treinamento de maneira mais geral.

Verdadeiro. É possível comparar as taxas de erro de validação estimadas em um conjunto de validação finita usando testes rápidos de estatística. No entanto, muitas vezes a variação de teste pode produzir diferenças estatisticamente significativas entre dois modelos treinados diferentes que usam as mesmas configurações de hiperparâmetro.

Estamos mais preocupados com a variação do estudo ao tentar tirar conclusões que vão além do nível de um ponto individual no espaço de hiperparâmetros. A variação do estudo depende do número de testes e do espaço de pesquisa. Vimos casos em que a variação do estudo é maior do que a variação de teste e casos em que é muito menor. Portanto, antes de adotar uma alteração candidata, considere executar o melhor teste N vezes para caracterizar a variação do teste de execução para execução. Normalmente, é possível reformular a variação do teste apenas após grandes alterações no pipeline, mas você pode precisar de estimativas mais recentes em alguns casos. Em outros aplicativos, caracterizar a variação de teste é muito cara para valer a pena.

Embora você só queira adotar alterações (incluindo novas configurações de hiperparâmetros) que produzam melhorias reais, exigir a certeza completa de que uma determinada alteração ajuda também não é a resposta certa. Portanto, se um novo ponto de hiperparâmetro (ou outra alteração) tiver um resultado melhor do que o valor de referência (levando em conta a variação de treinamento do novo ponto e do valor de referência o máximo possível), você provavelmente precisará adotá-lo como o novo valor de referência para comparações futuras. No entanto, recomendamos que você adote somente as alterações que produzem melhorias que superam as complexidades que adicionam.

Após a conclusão da exploração

Resumo: as ferramentas de otimização bayesianas são uma opção interessante quando você termina de pesquisar bons espaços de pesquisa e decide quais hiperparâmetros valem a pena ajustar.

Futuramente, suas prioridades não serão mais sobre o problema de ajuste, mas para produzir uma única configuração única para lançamento ou uso. Nesse momento, deve haver um espaço de pesquisa refinado que contenha confortavelmente a região local em torno da melhor avaliação observada e tenha sido adequadamente amostrada. Seu trabalho de exploração precisa ter revelado os hiperparâmetros mais essenciais a serem ajustados e os intervalos sensatos que podem ser usados para criar um espaço de pesquisa para um estudo final de ajuste automatizado usando o maior orçamento possível.

Como você não está mais preocupado em maximizar o insight sobre o problema de ajuste, muitas das vantagens da pesquisa quase aleatória não se aplicam mais. Portanto, use as ferramentas de otimização bayesianas para encontrar automaticamente a melhor configuração de hiperparâmetro. O Openier de código aberto implementa uma variedade de algoritmos sofisticados para ajustar modelos de ML, incluindo algoritmos de otimização bayesianos.

Suponha que o espaço de pesquisa contenha um volume não trivial de pontos de divisão, o que significa que os pontos que recebem perda de treinamento NaN ou até mesmo a perda de treinamento têm muitos desvios padrão piores do que a média. Nesse caso, recomendamos o uso de ferramentas de otimização de caixa preta que lidam adequadamente com testes que divergem. Consulte Otimização bayesiana com restrições desconhecidas para conhecer uma maneira excelente de lidar com esse problema. O Vizier de código aberto é compatível com a marcação de pontos divergentes marcando testes como inviáveis, embora ele não possa usar nossa abordagem preferida de Gelbart et al., dependendo de como está configurado.

Depois que a exploração for concluída, verifique o desempenho no conjunto de teste. Em princípio, você pode até mesmo dobrar o conjunto de validação no conjunto de treinamento e treinar novamente a melhor configuração encontrada com a otimização bayesiana. No entanto, isso é apropriado apenas se não houver lançamentos futuros com essa carga de trabalho específica (por exemplo, uma competição única da Kaggle).