Divisor exato para classificação binária com atributos numéricos

Nesta unidade, você conhecerá o algoritmo de divisor mais simples e comum que cria condições da forma $\mathrm{feature}_i \geq t$ na seguinte configuração:

• Tarefa de classificação binária
• Sem valores ausentes nos exemplos
• Sem índice pré-calculado nos exemplos

Suponha que um conjunto de exemplos de $n$ tenha um atributo numérico e um rótulo binário, `quot;orange" e "blue". Oficialmente, vamos descrever o conjunto de dados $D$ como:

$$D = \{(x_i,y_i)\}_{i\in[1,n]}$$

onde:

• $x_i$ é o valor de um atributo numérico em $\mathbb{R}$ (o conjunto de números reais).
• $y_i$ é um valor de marcador de classificação binária em {orange, blue}.

Nosso objetivo é encontrar um valor limite $t$ (threshold), de modo que a divisão dos exemplos $D$ nos grupos $T(rue)$ e $F(alse)$ de acordo com a condição $x_i \geq t$ melhora a separação dos rótulos. Por exemplo, mais exemplos de $quot;orange" em$ T $e mais $"blueF

A entropia de Hanhan é uma medida de transtorno. Para um marcador binário:

• A entropia Shannon é máxima quando os rótulos nos exemplos são equilibrados (50% azul e 50% laranja).
• A entropia Shannon é, no mínimo, (valor zero) quando os rótulos nos exemplos são puros (100% azul ou 100% laranja).

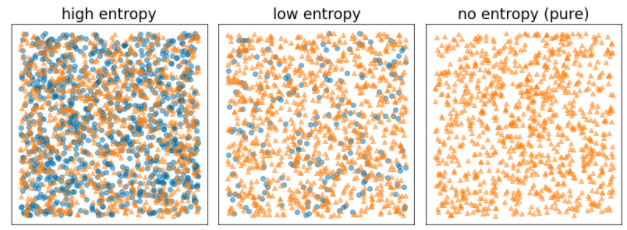
Figura 8. Três níveis diferentes de entropia.

 

Oficialmente, queremos encontrar uma condição que diminua a soma ponderada da entropia das distribuições de rótulos em $T$ e $F$. A pontuação correspondente é o ganho de informações, que é a diferença entre entropia de $D$'s e $$T$,$F$}. Essa diferença é chamada de ganho de informação.

A figura a seguir mostra uma divisão incorreta, em que a entropia permanece alta e as informações ganham baixa:

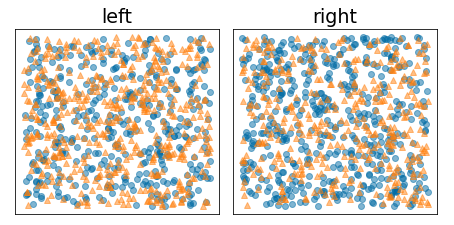
Figura 9. Uma divisão ruim não reduz a entropia do rótulo.

 

Por outro lado, a figura a seguir mostra uma divisão melhor em que a entropia se torna baixa (e as informações ganham alta):

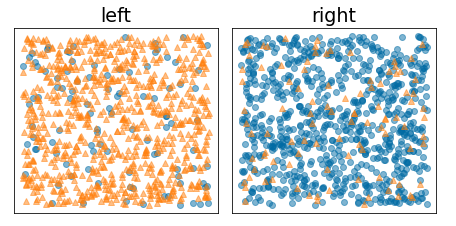
Figura 10. Uma boa divisão reduz a entropia do rótulo.

 

Oficialmente:

\[\begin{eqnarray} T & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \ge t \} \\[12pt] F & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \lt t \} \\[12pt] R(X) & = & \frac{\lvert \{ x | x \in X \ \textrm{and} \ x = \mathrm{pos} \} \rvert}{\lvert X \rvert} \\[12pt] H(X) & = & - p \log p - (1 - p) \log (1-p) \ \textrm{with} \ p = R(X)\\[12pt] IG(D,T,F) & = & H(D) - \frac {\lvert T\rvert} {\lvert D \rvert } H(T) - \frac {\lvert F \rvert} {\lvert D \rvert } H(F) \end{eqnarray}\]

onde:

• $IG(D,T,F)$ é o ganho das informações de dividir $D$ em $T$ e $F$.
• $H(X)$ é a entropia do conjunto de exemplos de $X$.
• $|X|$ é o número de elementos do conjunto $X$.
• $t$ é o valor do limite.
• $pos$ é o valor de rótulo positive, por exemplo, "quot;blue" no exemplo acima. Escolher um identificador diferente para ser "quot;positive label" não altera o valor da entropia ou o ganho de informações.
• $R(X)$ é a proporção de valores de rótulo positivos em exemplos $X$.
• $D$ é o conjunto de dados, conforme definido anteriormente nesta unidade.

No exemplo a seguir, consideramos um conjunto de dados de classificação binária com um único recurso numérico $x$. A figura a seguir mostra diferentes valores de limite $t$ (eixo X):

1. O histograma da característica $x$.
2. A proporção de exemplos em azul nos conjuntos $D$, $T$ e $F$ de acordo com o valor do limite.
3. A entropia em $D$, $T$ e $F$.
4. O ganho de informações, ou seja, o delta de entropia entre $D$ e {$T$,$F$}, ponderado pelo número de exemplos.

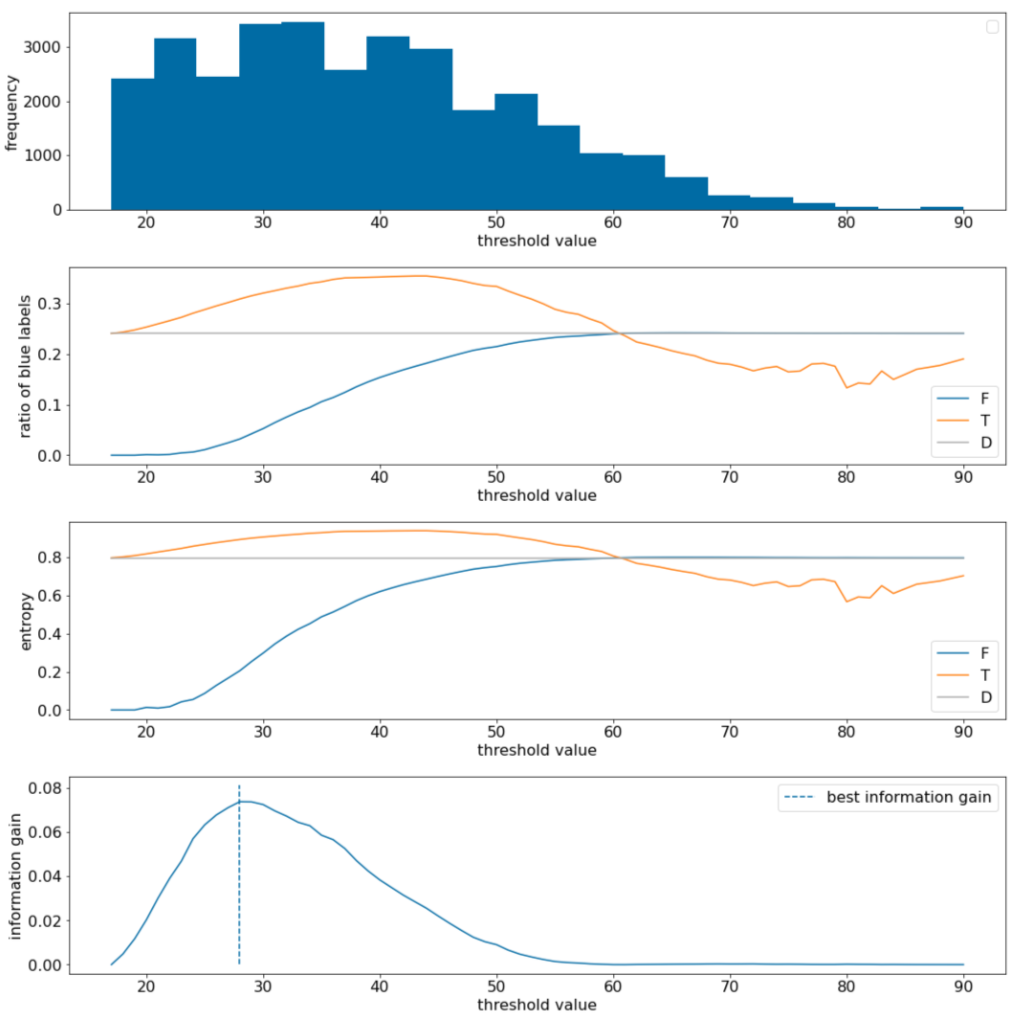
Figura 11. Quatro gráficos de limite.

 

Esses gráficos mostram o seguinte:

• O gráfico "frequency" mostra que as observações são relativamente bem distribuídas com concentrações entre 18 e 60. Uma propagação ampla de valor significa que há muitas divisões possíveis, o que é bom para treinar o modelo.

• A proporção de rótulos "azul" no conjunto de dados é de aproximadamente 25%. A linha "proporção de rótulo azul" mostra que, para valores de limite entre 20 e 50:

  • O conjunto $T$ contém um excesso de exemplos de etiquetas "blue" (até 35% para o limite 35).
  • O conjunto $F$ contém um déficit complementar de exemplos de etiquetas "blue" (somente 8% para o limite 35).

  Tanto a "proporção de rótulos azuis" quanto os gráficos "entropy" indicam que os rótulos podem ser relativamente bem separados nesse intervalo de limite.

• Esta observação é confirmada no gráfico de "ganhos de informação" O ganho máximo de informações é obtido com t~=28 para um valor de ganho de informação de aproximadamente 0,074. Portanto, a condição retornada pelo divisor será $x \geq 28$.

• O ganho de informações é sempre positivo ou nulo. A convergência ocorre em zero porque o valor limite atinge o valor máximo / mínimo. Nesses casos, $F$ ou $T$ fica vazio enquanto o outro contém todo o conjunto de dados e mostra uma entropia igual à de $D$. O ganho de informações também pode ser zero quando $H(T)$ = $H(F)$ = $H(D)$. No limite de 60, as proporções de "blue" identificadores $$ são iguais a $$$ e $$

Os valores candidatos para $t$ no conjunto de números reais ($\mathbb{R}$) são infinitos. No entanto, considerando um número finito de exemplos, existem apenas um número finito de divisões de $D$ em $T$ e $F$. Portanto, apenas um número finito de valores de $t$ é significativo para teste.

Uma abordagem clássica é classificar os valores x_i em ordem crescente de x_s(i), de modo que:

$$ x_{s(i)} \leq x_{s(i+1)} $$

Em seguida, teste $t$ para cada valor na metade entre valores ordenados consecutivos de $x_i$. Por exemplo, suponha que você tenha 1.000 valores de ponto flutuante de um recurso específico. Após a classificação, suponha que os dois primeiros valores sejam 8,5 e 8,7. Nesse caso, o primeiro valor do limite a ser testado seria 8.6.

Consideramos formalmente os seguintes valores candidatos para t:

$$ X = \left\{ \frac {x_{s(i)} + x_{s(i + 1)}} {2} \lvert x_{s(i)} \ne x_{s(i+1)} \right\} $$

A complexidade de tempo desse algoritmo é $\mathcal{O} ( n \log n) $ com $n$ o número de exemplos no nó (devido à classificação dos valores do atributo). Quando aplicado em uma árvore de decisão, o algoritmo do divisor é aplicado a cada nó e cada recurso. Observe que cada nó recebe aproximadamente 1/2 dos exemplos pai. Portanto, de acordo com o teorema principal, a complexidade de tempo do treinamento de uma árvore de decisão com esse divisor é:

$$ \mathcal{O} ( m n \log^2 n ) $$

onde:

• $m$ é o número de atributos.
• $n$ é o número de exemplos de treinamento.

Nesse algoritmo, o valor dos recursos não importa, somente a ordem. Por esse motivo, esse algoritmo funciona independentemente da escala ou da distribuição dos valores do atributo. Por isso, não precisamos normalizar nem dimensionar os atributos numéricos ao treinar uma árvore de decisão.