Exakte Trennlinie für binäre Klassifizierung mit numerischen Features

In diesem Modul lernen Sie den einfachsten und gängigsten Splitteralgorithmus kennen, der Bedingungen der Form „Attribut i ≥ t“ in der folgenden Umgebung erstellt:

• Binäre Klassifizierungsaufgabe
• Ohne fehlende Werte in den Beispielen
• Ohne vorab berechneten Index für die Beispiele

Angenommen, Sie haben eine Reihe von n Beispielen mit einem numerischen Merkmal und einem binären Label „orange“ und „blau“. Formal können wir den Datensatz D so beschreiben:

$$D = \{(x_i,y_i)\}_{i\in[1,n]}$$

Dabei gilt:

• $x_i$ ist der Wert eines numerischen Features in $\mathbb{R}$ (der Menge der reellen Zahlen).
• $y_i$ ist ein Labelwert für die binäre Klassifizierung aus {orange, blau}.

Unser Ziel ist es, einen Grenzwert t (Threshold) zu finden, durch den die Trennung der Labels verbessert wird, wenn die Beispiele D gemäß der Bedingung x ≥ t in die Gruppen „Wahr“ (T) und „Falsch“ (F) unterteilt werden. So gibt es beispielsweise mehr „orange“ Beispiele in T und mehr „blaue“ Beispiele in F.

Die Shannon-Entropie ist ein Maß für Unordnung. Für ein binäres Label:

• Die Shannon-Entropie ist maximal, wenn die Labels in den Beispielen ausgewogen sind (50% blau und 50% orange).
• Die Shannon-Entropie ist minimal (Wert 0), wenn die Labels in den Beispielen rein sind (100% blau oder 100% orange).

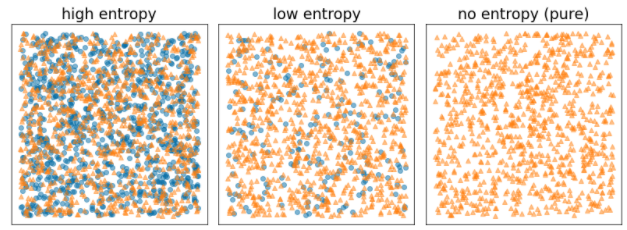
Abbildung 8. Drei verschiedene Entropieebenen.

 

Formell möchten wir eine Bedingung finden, die die gewichtete Summe der Entropie der Labelverteilungen in $T$ und $F$ verringert. Der entsprechende Wert ist der Informationsgewinn, also die Differenz zwischen der Entropie von $D$ und der Entropie von {$T$,$F$}. Dieser Unterschied wird als Informationsgewinn bezeichnet.

Die folgende Abbildung zeigt eine schlechte Aufteilung, bei der die Entropie hoch bleibt und der Informationsgewinn niedrig ist:

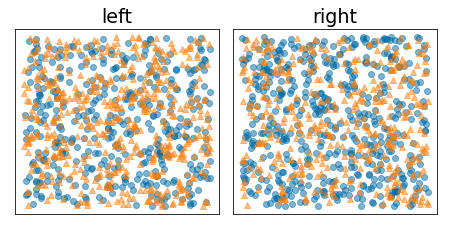
Abbildung 9. Eine schlechte Aufteilung reduziert die Entropie des Labels nicht.

 

Im folgenden Diagramm ist dagegen eine bessere Aufteilung zu sehen, bei der die Entropie niedrig (und der Informationsgewinn hoch) ist:

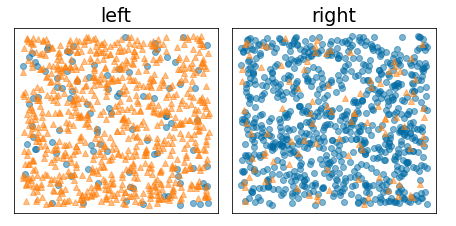
Abbildung 10. Eine gute Aufteilung reduziert die Entropie des Labels.

 

Formell:

\[\begin{eqnarray} T & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \ge t \} \\[12pt] F & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \lt t \} \\[12pt] R(X) & = & \frac{\lvert \{ x | x \in X \ \textrm{and} \ x = \mathrm{pos} \} \rvert}{\lvert X \rvert} \\[12pt] H(X) & = & - p \log p - (1 - p) \log (1-p) \ \textrm{with} \ p = R(X)\\[12pt] IG(D,T,F) & = & H(D) - \frac {\lvert T\rvert} {\lvert D \rvert } H(T) - \frac {\lvert F \rvert} {\lvert D \rvert } H(F) \end{eqnarray}\]

Dabei gilt:

• $IG(D,T,F)$ ist der Informationsgewinn, der durch die Aufteilung von D in T und F erzielt wird.
• H(X) ist die Entropie der Beispielmenge X.
• $|X|$ ist die Anzahl der Elemente im Satz X.
• $t$ ist der Grenzwert.
• $pos$ ist der positive Labelwert, z. B. „blau“ im Beispiel oben. Wenn Sie ein anderes Label als „positives Label“ auswählen, ändert sich der Wert der Entropie oder des Informationsgewinns nicht.
• R(X) ist das Verhältnis der positiven Labelwerte in den Beispielen X.
• „D“ ist der Datensatz (wie oben in dieser Einheit definiert).

Im folgenden Beispiel betrachten wir einen Datensatz für die binäre Klassifizierung mit einem einzelnen numerischen Merkmal x. Die folgende Abbildung zeigt für verschiedene Schwellenwerte t (x-Achse):

1. Das Histogramm des Merkmals x.
2. Das Verhältnis der „blauen“ Beispiele in den Mengen D, T und F gemäß dem Grenzwert.
3. Die Entropie in $D$, $T$ und $F$.
4. Der Informationsgewinn, d. h. die Entropiedifferenz zwischen $D$ und {$T$,$F$}, gewichtet durch die Anzahl der Beispiele.

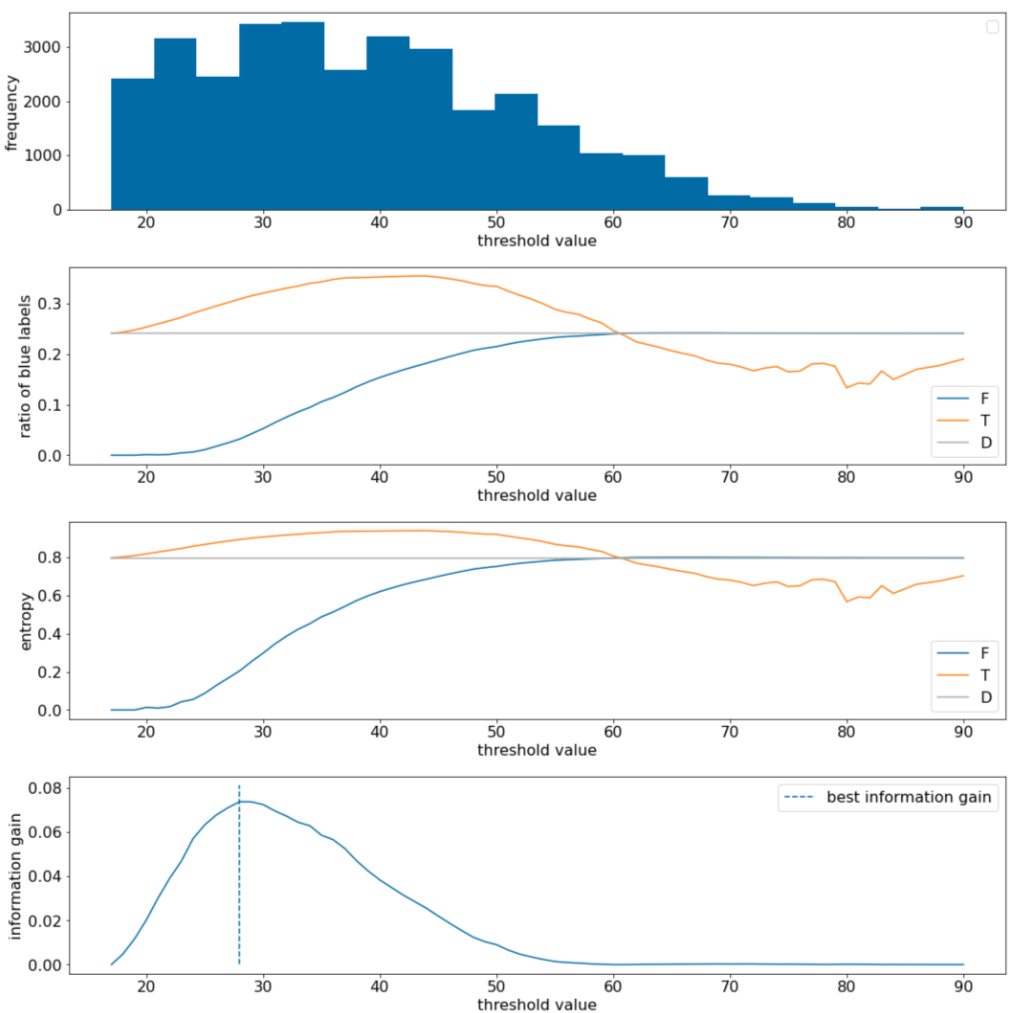
Abbildung 11. Vier Schwellenwertdiagramme.

 

Diese Diagramme zeigen Folgendes:

• Das Diagramm „Häufigkeit“ zeigt, dass die Beobachtungen mit Konzentrationen zwischen 18 und 60 relativ gut verteilt sind. Eine große Streuung der Werte bedeutet, dass es viele potenzielle Aufteilungen gibt, was für das Training des Modells von Vorteil ist.

• Das Verhältnis der blauen Labels im Datensatz beträgt etwa 25%. Im Diagramm „Anteil der blauen Kennzeichnung“ ist zu sehen, dass bei Schwellenwerten zwischen 20 und 50 Folgendes gilt:

  • Der Satz $T$ enthält zu viele Beispiele für das Label „blau“ (bis zu 35% bei einem Grenzwert von 35).
  • Der Satz F enthält ein komplementäres Defizit an Beispielen für das blaue Label (nur 8% für den Grenzwert 35).

  Sowohl das Diagramm „Anteil der blauen Labels“ als auch das Diagramm „Entropie“ zeigen, dass die Labels in diesem Bereich des Grenzwerts relativ gut voneinander getrennt werden können.

• Diese Beobachtung wird im Diagramm „Informationsgewinn“ bestätigt. Der maximale Informationsgewinn wird bei t=28 mit einem Wert von etwa 0,074 erreicht. Die vom Splitter zurückgegebene Bedingung lautet daher $x \geq 28$.

• Der Informationsgewinn ist immer positiv oder null. Er konvergiert gegen Null, wenn der Grenzwert gegen seinen Maximal-/Minimalwert konvergiert. In diesen Fällen ist entweder $F$ oder $T$ leer, während das andere den gesamten Datensatz enthält und eine Entropie aufweist, die der in $D$ entspricht. Der Informationsgewinn kann auch null sein, wenn $H(T)$ = $H(F)$ = $H(D)$. Bei einem Grenzwert von 60 % sind die Anteile der blauen Labels sowohl für $T$ als auch für $F$ gleich denen von $D$ und der Informationsgewinn ist null.

Die Kandidaten für $t$ im Komplex sind unendlich. Bei einer endlichen Anzahl von Beispielen gibt es jedoch nur eine endliche Anzahl von Teilungen von D in T und F. Daher ist nur eine endliche Anzahl von Werten für t sinnvoll zu testen.

Ein klassischer Ansatz besteht darin, die Werte x_i in aufsteigender Reihenfolge zu sortieren, wobei x_s(i) gilt:

$$ x_{s(i)} \leq x_{s(i+1)} $$

Testen Sie dann t für jeden Wert, der genau in der Mitte zwischen zwei aufeinanderfolgenden sortierten Werten von x liegt. Angenommen, Sie haben 1.000 Fließkommawerte für ein bestimmtes Merkmal. Angenommen, nach der Sortierung sind die ersten beiden Werte 8,5 und 8,7. In diesem Fall wäre der erste zu testende Grenzwert 8, 6.

Formell betrachten wir die folgenden Kandidatenwerte für t:

$$ X = \left\{ \frac {x_{s(i)} + x_{s(i + 1)}} {2} \lvert x_{s(i)} \ne x_{s(i+1)} \right\} $$

Die Zeitkomplexität dieses Algorithmus ist $\mathcal{O} ( n \log n) $, wobei n die Anzahl der Beispiele im Knoten ist (aufgrund der Sortierung der Featurewerte). Bei der Anwendung auf einen Entscheidungsbaum wird der Trennalgorithmus auf jeden Knoten und jedes Merkmal angewendet. Beachten Sie, dass jeder Knoten etwa die Hälfte seiner übergeordneten Beispiele erhält. Gemäß dem Mastertheorem ist die Zeitkomplexität des Trainings eines Entscheidungsbaums mit diesem Splitter daher:

$$ \mathcal{O} ( m n \log^2 n ) $$

Dabei gilt:

• $m$ ist die Anzahl der Merkmale.
• n ist die Anzahl der Trainingsbeispiele.

Bei diesem Algorithmus spielt der Wert der Features keine Rolle, nur die Reihenfolge. Daher funktioniert dieser Algorithmus unabhängig von der Skalierung oder Verteilung der Feature-Werte. Daher müssen wir die numerischen Merkmale beim Trainieren eines Entscheidungsbaums nicht normalisieren oder skalieren.