ביחידה הזו נסביר על האלגוריתם הפשוט והנפוץ ביותר לחלוקה, שיוצר תנאים מהסוג $\mathrm{feature}_i \geq t$ בהגדרה הבאה:
- משימה של סיווג בינארי
- ללא ערכים חסרים בדוגמאות
- ללא אינדקס מחושב מראש בדוגמאות
נניח שיש קבוצה של n דוגמאות עם מאפיין מספרי ותווית בינארית 'כתום' ו'כחול'. באופן רשמי, נתייחס למערך הנתונים D באופן הבא:
where:
- $x_i$ הוא הערך של מאפיין מספרי ב-$\mathbb{R}$ (קבוצת המספרים הממשיים).
- הערך של $y_i$ הוא ערך של תווית סיווג בינארי מתוך {orange, blue}.
המטרה שלנו היא למצוא ערך סף t (סף) כך שחלוקת הדוגמאות D לקבוצות T(true) ו-F(false) בהתאם לתנאי x_i \geq t תשפר את ההפרדה בין התוויות. לדוגמה, יותר דוגמאות 'כתום' ב-T ויותר דוגמאות 'כחול' ב-F.
אנטרופיה של שרנון היא מדד של אי-סדר. בתווית בינארית:
- האנטרופיה של שרנון היא המקסימלית כשהתוויות בדוגמאות מאוזנות (50% כחול ו-50% כתום).
- האנטרופיה של שרנון היא מינימלית (ערך אפס) כשהתוויות בדוגמאות הן טהורות (100% כחול או 100% כתום).
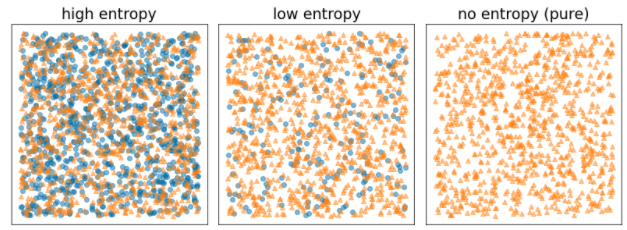
איור 8. שלוש רמות אנטרופי שונות.
באופן רשמי, אנחנו רוצים למצוא תנאי שמקטין את הסכום המשוקלל של האנטרופי של התפלגויות התוויות ב-T וב-F. הציון התואם הוא רווח המידע, שהוא ההפרש בין האנטרופי של D לבין האנטרופי של {T,F}. ההפרש הזה נקרא רווח מידע.
באיור הבא מוצג פילוח לא טוב, שבו האנטרופיה נשארת גבוהה והרווח המידעי נמוך:
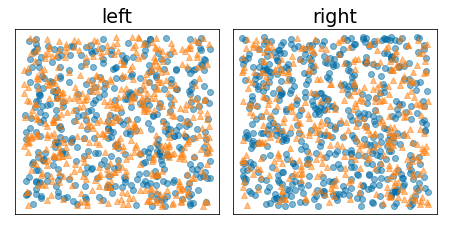
איור 9. חלוקה לא טובה לא מפחיתה את האנטרופיה של התווית.
לעומת זאת, באיור הבא מוצגת חלוקה טובה יותר שבה האנטרופיה קטנה (והרווח המידעי גבוה):
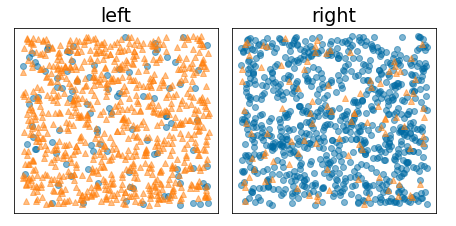
איור 10. חלוקה טובה מפחיתה את האנטרופיה של התווית.
באופן רשמי:
\[\begin{eqnarray} T & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \ge t \} \\[12pt] F & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \lt t \} \\[12pt] R(X) & = & \frac{\lvert \{ x | x \in X \ \textrm{and} \ x = \mathrm{pos} \} \rvert}{\lvert X \rvert} \\[12pt] H(X) & = & - p \log p - (1 - p) \log (1-p) \ \textrm{with} \ p = R(X)\\[12pt] IG(D,T,F) & = & H(D) - \frac {\lvert T\rvert} {\lvert D \rvert } H(T) - \frac {\lvert F \rvert} {\lvert D \rvert } H(F) \end{eqnarray}\]
where:
- $IG(D,T,F)$ הוא הרווח המידעי מהפיצול של $D$ ל-T ול-F.
- $H(X)$ היא האנטרופיה של קבוצת הדוגמאות $X$.
- הערך של $|X|$ הוא מספר הרכיבים בקבוצה $X$.
- $t$ הוא ערך הסף.
- $pos$ הוא ערך התווית החיובי, לדוגמה, 'כחול' בדוגמה שלמעלה. בחירת תווית אחרת בתור 'תווית חיובית' לא משנה את הערך של האנטרופיה או את הרווח המידעי.
- $R(X)$ הוא היחס של ערכי התוויות החיוביים בדוגמאות $X$.
- $D$ הוא מערך הנתונים (כפי שהוגדר קודם לכן ביחידה הזו).
בדוגמה הבאה נבחן מערך נתונים של סיווג בינארי עם מאפיין מספרי יחיד x. באיור הבא מוצגים ערכים שונים של הסף t (ציר x):
- ההיסטוגרמה של המאפיין x.
- היחס בין הדוגמאות 'כחולות' בקבוצות $D$, $T$ ו-$F$, בהתאם לערך הסף.
- האנטרופיה ב-D, ב-T וב-F.
- רווח המידע, כלומר הדלתה של האנטרופיה בין $D$ לבין {$T$,$F$} שמשוקללת לפי מספר הדוגמאות.
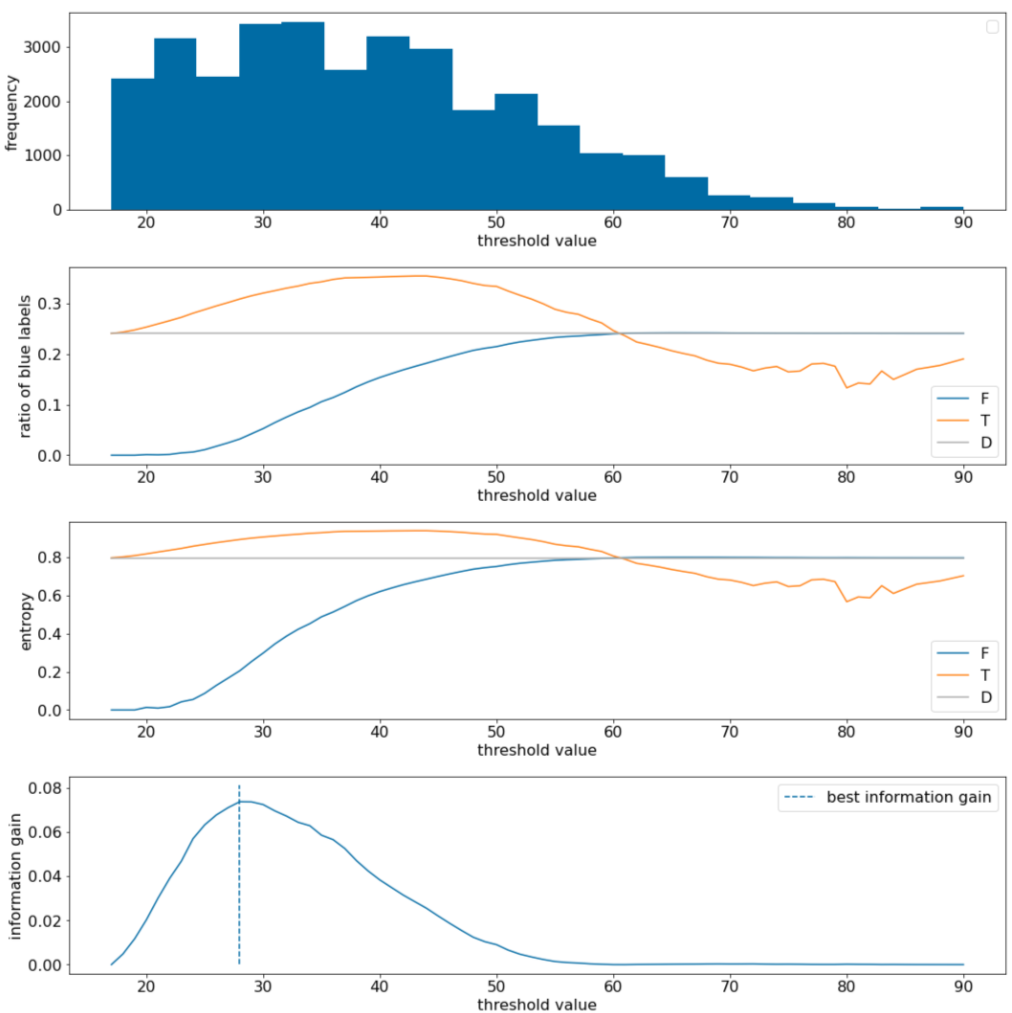
איור 11. ארבע תרשימים של ערכי סף.
בתרשים הזה מוצגים הנתונים הבאים:
- בתרשים 'תדירות' מוצג שהתצפיות מפוזרות באופן יחסי, עם ריכוזים בין 18 ל-60. אם יש טווח רחב של ערכים, יש הרבה חלוקות פוטנציאליות, וזה טוב לאימון המודל.
היחס של התוויות הכחולות במערך הנתונים הוא כ-25%. בתרשים 'יחס התווית הכחולה' מוצג שעבור ערכי סף בין 20 ל-50:
- הקבוצה $T$ מכילה יותר מדי דוגמאות של תוויות 'כחול' (עד 35% אם הסף הוא 35).
- קבוצת $F$ מכילה חסכון משלים של דוגמאות לתווית 'כחולה' (רק 8% עבור הסף 35).
גם התרשימים של 'יחס התוויות הכחולות' וגם התרשימים של 'אנטרופיה' מצביעים על כך שאפשר להפריד את התוויות באופן יחסי טוב בטווח הסף הזה.
התצפית הזו מאומתת בתרשים 'שיפור המידע'. אנחנו רואים שהרווח המרבי במידע מתקבל כאשר t~=28, עם ערך של רווח המידע של ~0.074. לכן, התנאי שהמפצל מחזיר יהיה $x \geq 28$.
הרווח המידעי הוא תמיד חיובי או אפס. הוא מתקרב לאפס כאשר ערך הסף מתקרב לערך המקסימלי או המינימלי שלו. במקרים כאלה, המאפיין $F$ או המאפיין $T$ הופכים ריקים, והמאפיין השני מכיל את מערך הנתונים כולו ומציג אנטרופיה שווה לזו של המאפיין $D$. רווח המידע יכול להיות אפס גם כאשר $H(T)$ = $H(F)$ = $H(D)$. בערך הסף 60, היחסים של התוויות 'כחול' גם למאפיין $T$ וגם למאפיין $F$ זהים ליחסים של המאפיין $D$, ורווחי המידע הוא אפס.
יש אינסוף ערכים מועמדים ל-t בקבוצת המספרים הממשיים ($\mathbb{R}$). עם זאת, אם יש מספר סופי של דוגמאות, קיים רק מספר סופי של חלוקות של D ל-T ול-F. לכן, רק מספר סופי של ערכים של t מועילים לבדיקה.
גישה קלאסית היא למיין את הערכים xi בסדר עולה xs(i) כך ש:
לאחר מכן, בודקים את $t$ לכל ערך באמצע בין ערכים ממוינים רצופים של $x_i$. לדוגמה, נניח שיש לכם 1,000 ערכים של נקודה צפה של מאפיין מסוים. אחרי המיון, נניח ששני הערכים הראשונים הם 8.5 ו-8.7. במקרה הזה, ערך הסף הראשון לבדיקה יהיה 8.6.
באופן רשמי, אנחנו מביאים בחשבון את הערכים הבאים של t:
מורכבות הזמן של האלגוריתם הזה היא $\mathcal{O} ( n \log n) $, כאשר n הוא מספר הדוגמאות בצומת (בגלל המיון של ערכי המאפיינים). כשמחילים את האלגוריתם על עץ החלטות, הוא מופעל על כל צומת ועל כל מאפיין. שימו לב שכל צומת מקבל כמחצית מהדוגמאות של ההורה שלו. לכן, לפי המשפט הראשי, מורכבות הזמן של אימון עץ החלטות עם המפריד הזה היא:
where:
- m הוא מספר המאפיינים.
- n הוא מספר הדוגמאות לאימון.
באלגוריתם הזה, הערך של המאפיינים לא משנה, רק הסדר משנה. לכן, האלגוריתם הזה פועל באופן עצמאי מהסולם או מההפצה של ערכי המאפיינים. לכן אין צורך לבצע נורמליזציה או שינוי קנה מידה של המאפיינים המספריים כשמאמנים עץ החלטות.