W tej jednostce poznasz najprostszy i najczęściej stosowany algorytm splittera, który tworzy warunki w formie $\mathrm{feature}_i \geq t$ w tych ustawieniach:
- Zadanie binarnej klasyfikacji
- Przykłady bez brakujących wartości
- Bez wstępnie obliczonego indeksu w przypadku przykładów
Załóżmy, że mamy zbiór $n$ przykładów z cechą liczbową i etykietą binarną „pomarańczowy” i „niebieski”. Formalnie zbiór danych $D$ można opisać w ten sposób:
gdzie:
- $x_i$ to wartość cechy liczbowej w $\mathbb{R}$ (zbiorze liczb rzeczywistych).
- $y_i$ to binarna wartość etykiety klasyfikacji w skali {pomarańczowy, niebieski}.
Naszym celem jest znalezienie wartości progowej $t$ (progres) takiej, aby podział przykładów $D$ na grupy $T(rue)$ i $F(alse)$ zgodnie z warunkiem $x_i \geq t$ poprawiał rozdzielność etykiet, np. więcej przykładów „pomarańczowych” w grupie $T$ i więcej przykładów „niebieskich” w grupie $F$.
Entropia Shannona to miara nieuporządkowania. Etykieta binarna:
- Entropia Shannona osiąga maksimum, gdy etykiety w przykładach są zrównoważone (50% niebieskiego i 50% pomarańczowego).
- Entropia Shannona jest minimalna (wartość 0), gdy etykiety w przykladach są czyste (100% niebieski lub 100% pomarańczowy).
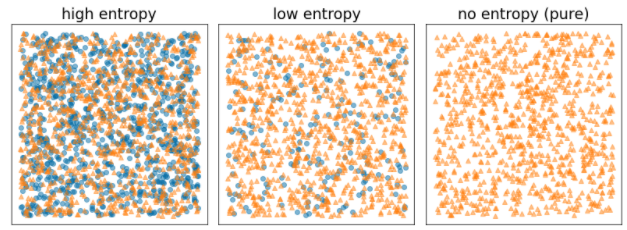
Rysunek 8. 3 poziomy entropii.
Formalnie chcemy znaleźć warunek, który zmniejsza ważoną sumę entropii rozkładu etykiet w $T$ i $F$. Odpowiadająca temu wartość to wzrost informacji, który jest różnicą między entropią $D$ i entropią {$T$,$F$}. Ta różnica nazywana jest wzrostem informacji.
Rysunek poniżej przedstawia niekorzystny podział, w którym entropia pozostaje wysoka, a zysk informacji jest niski:
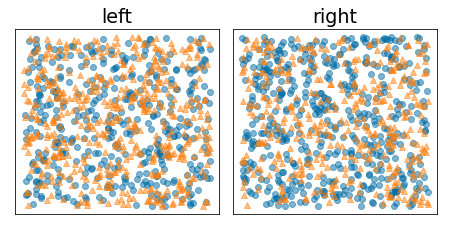
Rysunek 9. Nieudany podział nie zmniejsza entropii etykiety.
Natomiast na rysunku poniżej widać lepszy podział, w którym entropia jest niska (a informacyjność – wysoka):
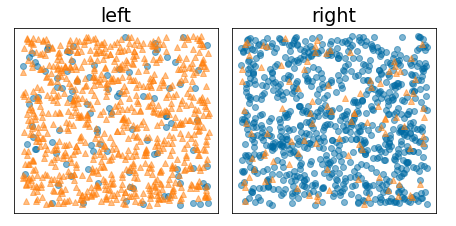
Rysunek 10. Dobry podział zmniejsza entropię etykiety.
Formalnie:
\[\begin{eqnarray} T & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \ge t \} \\[12pt] F & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \lt t \} \\[12pt] R(X) & = & \frac{\lvert \{ x | x \in X \ \textrm{and} \ x = \mathrm{pos} \} \rvert}{\lvert X \rvert} \\[12pt] H(X) & = & - p \log p - (1 - p) \log (1-p) \ \textrm{with} \ p = R(X)\\[12pt] IG(D,T,F) & = & H(D) - \frac {\lvert T\rvert} {\lvert D \rvert } H(T) - \frac {\lvert F \rvert} {\lvert D \rvert } H(F) \end{eqnarray}\]
gdzie:
- $IG(D,T,F)$ to zyski informacyjne z podziału zbioru $D$ na zbiory $T$ i $F$.
- $H(X)$ to entropia zbioru przykładów $X$.
- $|X|$ to liczba elementów w zbiorze $X$.
- $t$ to wartość progowa.
- $pos$ to dodatnia wartość etykiety, np. „niebieski” w przykładzie powyżej. Wybranie innej etykiety jako „etykiety pozytywnej” nie zmienia wartości entropii ani zysku informacyjnego.
- $R(X)$ to stosunek wartości dodatnich etykiet w przypadku przykładów $X$.
- $D$ to zbiór danych (zdefiniowany wcześniej w tym module).
W tym przykładzie rozważamy zbiór danych do klasyfikacji binarnej z jedną cechą numeryczną $x$. Na rysunku poniżej dla różnych wartości progu $t$ (oś X) przedstawiono:
- Histogram funkcji $x$.
- Stosunek przykładów „niebieski” w zbiorach $D$, $T$ i $F$ zgodnie z wartością progową.
- entropia w $D$, $T$ i $F$;
- Zysk informacji, czyli różnica entropii między $D$ a {$T$,$F$} zważona przez liczbę przykładów.
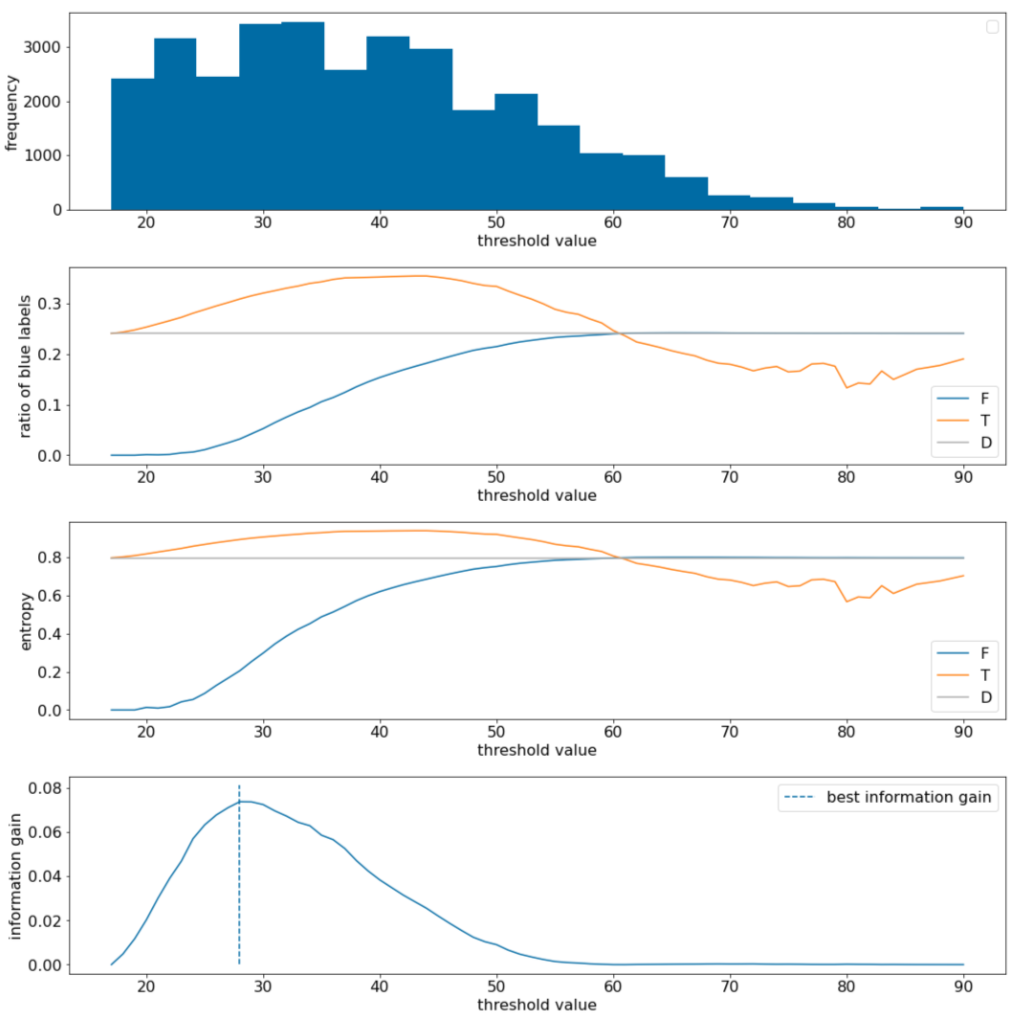
Rysunek 11. 4 wykresy progów.
Te wykresy przedstawiają:
- Wykres „częstotliwość” pokazuje, że obserwacje są stosunkowo dobrze rozłożone, a ich skoncentrowanie się na wartościach od 18 do 60. Szeroki zakres wartości oznacza, że istnieje wiele potencjalnych podziałów, co jest korzystne dla trenowania modelu.
Stosunek etykiet „niebieskich” w zbiorze danych wynosi ok. 25%. Wykres „stosunek niebieskiej etykiety” pokazuje, że w przypadku wartości progowych od 20 do 50:
- Zbiór $T$ zawiera nadmiar przykładów etykiet „niebieskich” (do 35% dla progu 35).
- Zestaw $F$ zawiera uzupełniający deficyt przykładów etykiet „niebieskich” (tylko 8% dla progu 35).
Zarówno wykres „stosunek niebieskich etykiet” (ang. „ratio of blue labels”), jak i wykres „entropii” (ang. „entropy”) wskazują, że w tym zakresie progu etykiety można stosunkowo dobrze rozdzielić.
To spostrzeżenie potwierdza wykres „wzrost informacji”. Widzimy, że maksymalny przyrost informacji uzyskujemy przy t ≈ 28, a jego wartość wynosi ~0,074. Dlatego warunek zwracany przez splitter będzie miał postać $x \geq 28$.
Zysk informacji jest zawsze dodatni lub równy 0. Zbliża się do zera, gdy wartość progowa zbliża się do wartości maksymalnej lub minimalnej. W takich przypadkach albo $F$, albo $T$ staje się pusty, a drugi z nich zawiera cały zbiór danych i wyświetla entropię równą entropii w $D$. Zysk informacji może też wynosić 0, gdy $H(T)$ = $H(F)$ = $H(D)$. Przy progu 60 proporcje etykiet „niebieskich” zarówno dla $T$, jak i dla $F$ są takie same jak w $D$, a wzrost informacji wynosi 0.
Wartości kandydatów dla $t$ w zbiorze liczb rzeczywistych ($\mathbb{R}$) są nieskończenie. Jednak ze względu na ograniczoną liczbę przykładów istnieje tylko skończona liczba podziałów zbioru $D$ na zbiory $T$ i $F$. Dlatego tylko skończona liczba wartości $t$ jest istotna dla testu.
Klasycznym podejściem jest sortowanie wartości xi w rosnącej kolejności xs(i), tak aby:
Następnie przetestuj $t$ dla każdej wartości leżącej w połowie odległości między kolejnymi posortowanymi wartościami funkcji $x_i$. Załóżmy na przykład, że masz 1000 wartości zmiennoprzecinkowych danej cechy. Po posortowaniu załóżmy, że pierwsze 2 wartości to 8,5 i 8,7. W tym przypadku pierwszą wartością progową do przetestowania będzie 8, 6.
Formalnie rozważamy te wartości kandydatów dla t:
Złożoność czasowa tego algorytmu to $\mathcal{O} ( n \log n) $, gdzie $n$ to liczba przykładów w węźle (z powodu sortowania wartości cech). Gdy jest stosowany w drzewie decyzyjnym, algorytm rozdzielania jest stosowany do każdego węzła i każdej cechy. Pamiętaj, że każdy węzeł otrzymuje około połowy przykładów swojego rodzica. Dlatego zgodnie z twierdzeniem głównym złożoność czasową trenowania schematu decyzyjnego za pomocą tego rozdrabniania można wyrazić w ten sposób:
gdzie:
- $m$ to liczba cech.
- $n$ to liczba przykładów treningowych.
W tym algorytmie nie ma znaczenia, jakie są wartości funkcji – liczy się tylko kolejność. Z tego powodu działa niezależnie od skali lub dystrybucji wartości cech. Dlatego podczas trenowania drzewa decyzyjnego nie trzeba normalizować ani skalować cech liczbowych.