适用于包含数值特征的二元分类的精确分屏器

在本单元中，您将探索最简单、最常见的分屏算法，该算法会在以下设置中创建形式为 $\mathrm{feature}_i \geq t$ 的条件：

• 二元分类任务
• 示例中没有缺失值
• 未对示例预计算索引

假设有一组 $n$ 个示例，其中包含一个数值特征和一个二元标签“橙色”和“蓝色”。形式上，我们将数据集 $D$ 描述为：

$$D = \{(x_i,y_i)\}_{i\in[1,n]}$$

其中：

• $x_i$ 是 $\mathbb{R}$（实数集）中的数值特征的值。
• $y_i$ 是 {orange, blue} 中的二元分类标签值。

我们的目标是找到一个阈值 $t$（阈值），使得根据 $x_i \geq t$ 条件将示例 $D$ 划分为 $T(rue)$ 和 $F(alse)$ 组，从而改进标签分离效果；例如，$T$ 中包含更多“橙色”示例，$F$ 中包含更多“蓝色”示例。

香农熵是一种混乱程度的衡量标准。对于二元标签：

• 当示例中的标签平衡（50% 为蓝色，50% 为橙色）时，香农熵最大。
• 如果示例中的标签是纯色（100% 蓝色或 100% 橙色），则香农熵最小（值为 0）。

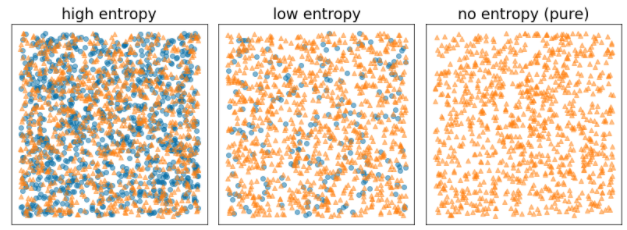
图 8. 三种不同的熵级别。

 

形式上，我们希望找到一个条件，以降低 $T$ 和 $F$ 中的标签分布熵的加权和。相应的得分是信息增益，即 $D$ 的熵与 {$T$,$F$} 熵之间的差值。这项差异称为信息增益。

下图显示了一种不良的拆分，其中熵保持较高，信息增益较低：

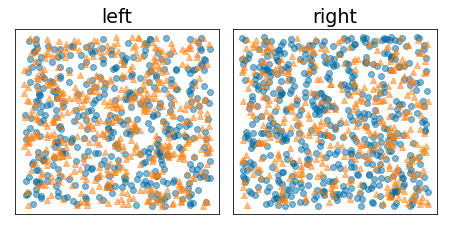
图 9. 糟糕的分块不会降低标签的熵。

 

相比之下，下图显示了一种更好的分块，其中熵变低（信息增益变高）：

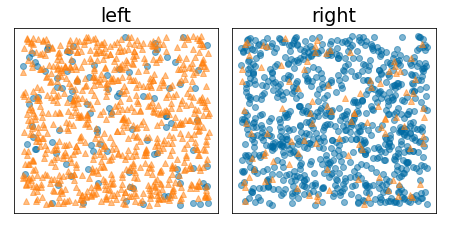
图 10. 良好的分块可降低标签的熵。

 

正式：

\[\begin{eqnarray} T & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \ge t \} \\[12pt] F & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \lt t \} \\[12pt] R(X) & = & \frac{\lvert \{ x | x \in X \ \textrm{and} \ x = \mathrm{pos} \} \rvert}{\lvert X \rvert} \\[12pt] H(X) & = & - p \log p - (1 - p) \log (1-p) \ \textrm{with} \ p = R(X)\\[12pt] IG(D,T,F) & = & H(D) - \frac {\lvert T\rvert} {\lvert D \rvert } H(T) - \frac {\lvert F \rvert} {\lvert D \rvert } H(F) \end{eqnarray}\]

其中：

• $IG(D,T,F)$ 是将 $D$ 拆分为 $T$ 和 $F$ 的信息增益。
• $H(X)$ 是样本集 $X$ 的熵。
• $|X|$ 是集合 $X$ 中的元素数量。
• $t$ 是阈值。
• $pos$ 是正面标签值，例如上例中的“blue”。选择其他标签作为“正例标签”不会改变熵或信息增益的值。
• $R(X)$ 是样本 $X$ 中正例标签值的比率。
• $D$ 是数据集（如本单元前面所定义）。

在以下示例中，我们考虑一个包含单个数值特征 $x$ 的二元分类数据集。下图显示了对于不同的阈值 $t$ 值（x 轴）：

1. 特征 $x$ 的直方图。
2. 根据阈值的大小，$D$、$T$ 和 $F$ 集中“蓝色”示例的比例。
3. $D$、$T$ 和 $F$ 中的熵。
4. 信息增益；即 $D$ 与 {$T$,$F$} 之间的熵差，乘以示例数量。

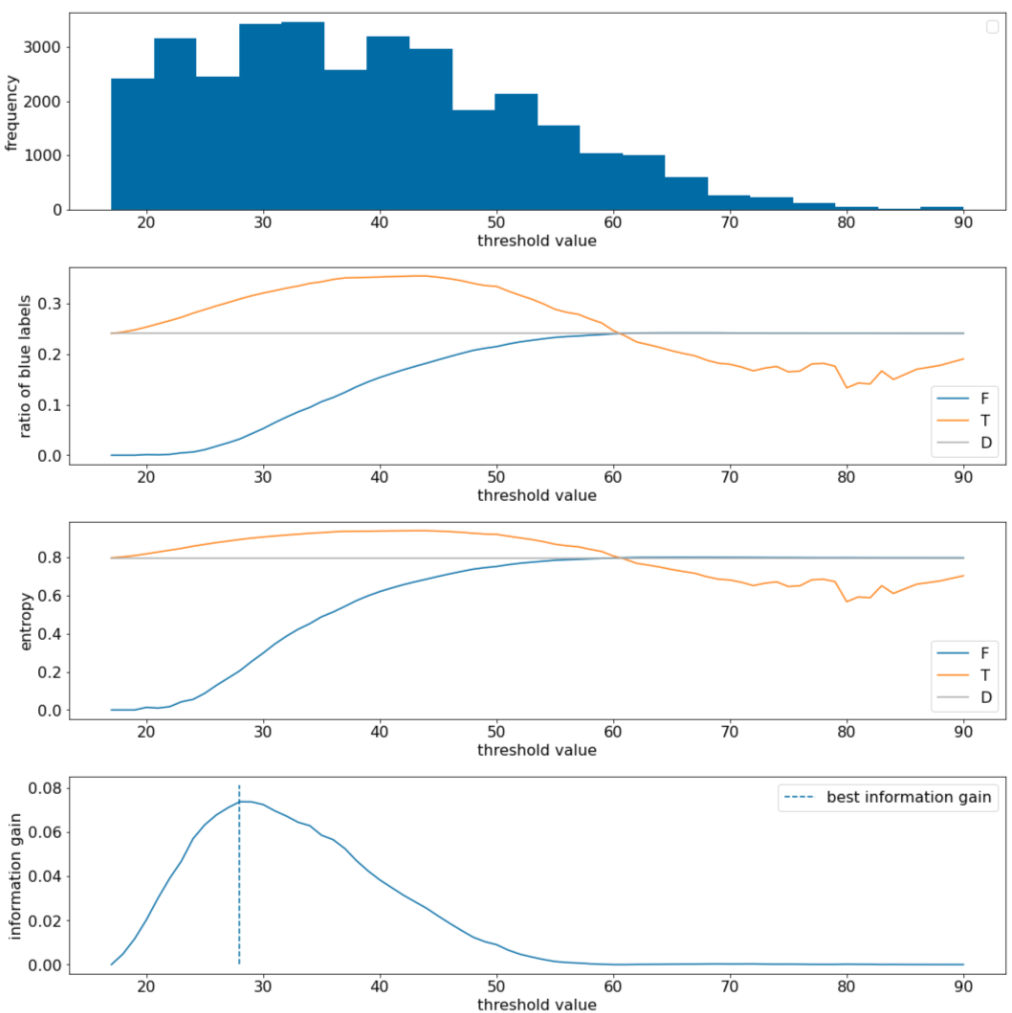
图 11. 四个阈值图。

 

这些图表会显示以下内容：

• “频率”图表显示，观察结果分布相对均匀，浓度介于 18 到 60 之间。值范围较大意味着存在许多潜在的分块，这对训练模型很有帮助。

• 数据集中“蓝色”标签的比例约为 25%。“蓝色标签的比例”图表显示，对于介于 20 到 50 之间的阈值值：

  • $T$ 集包含过多的“蓝色”标签示例（如果阈值为 35，则最多占 35%）。
  • $F$ 集包含“蓝色”标签示例的补充缺口（阈值为 35 时仅为 8%）。

  “蓝色标签的比例”和“熵”图表均表明，在该阈值范围内，标签可以相对较好地分离。

• “信息增益”图表证实了这一点。我们发现，当 t 约为 28 时，信息增益最大，信息增益值约为 0.074。因此，分屏器返回的条件将为 $x \geq 28$。

• 信息增益始终为正数或 null。随着阈值趋近于最大值 / 最小值，该值会趋近于零。在这些情况下，$F$ 或 $T$ 会变为空，而另一个集合包含整个数据集，并且熵等于 $D$ 中的熵。当 $H(T)$ = $H(F)$ = $H(D)$ 时，信息增益也可能为零。在阈值为 60 时，$T$ 和 $F$ 的“蓝色”标签比例与 $D$ 相同，并且信息增益为零。

实数集 ($\mathbb{R}$) 中的 $t$ 候选值无限。但是，对于有限数量的示例，$D$ 只能以有限的方式划分为 $T$ 和 $F$。因此，只有有限数量的 $t$ 值有意义。

传统方法是按升序 x_s(i) 对值 x_i 进行排序，以便：

$$ x_{s(i)} \leq x_{s(i+1)} $$

然后，针对 $x_i$ 的连续排序值中间的每个值测试 $t$。例如，假设您有 1,000 个特定特征的浮点值。假设排序后，前两个值分别为 8.5 和 8.7。在本例中，要测试的第一个阈值为 8.6。

正式地，我们考虑以下 t 候选值：

$$ X = \left\{ \frac {x_{s(i)} + x_{s(i + 1)}} {2} \lvert x_{s(i)} \ne x_{s(i+1)} \right\} $$

此算法的时间复杂度为 $\mathcal{O} ( n \log n) $，其中 $n$ 是节点中的示例数量（由于特征值的排序）。在决策树上应用时，分屏算法会应用于每个节点和每个特征。请注意，每个节点会收到其父级示例的约 1/2。因此，根据主定理，使用此拆分器训练决策树的时间复杂度为：

$$ \mathcal{O} ( m n \log^2 n ) $$

其中：

• $m$ 是特征数。
• $n$ 是训练示例的数量。

在此算法中，特征的值无关紧要；只有顺序才重要。因此，此算法的工作方式与特征值的规模或分布无关。因此，在训练决策树时，我们无需对数值特征进行归一化或缩放。