ในยูนิตนี้ คุณจะได้สํารวจอัลกอริทึมตัวแยกที่ง่ายที่สุดและพบบ่อยที่สุด ซึ่งสร้างเงื่อนไขในรูปแบบ $\mathrm{feature}_i \geq t$ ในการตั้งค่าต่อไปนี้
- งานการจัดประเภทแบบไบนารี
- ไม่มีค่าที่ขาดหายไปในตัวอย่าง
- ไม่มีดัชนีที่คำนวณไว้ล่วงหน้าในตัวอย่าง
สมมติชุดตัวอย่าง $n$ ชุดที่มีฟีเจอร์ตัวเลขและป้ายกำกับแบบไบนารี นั่นคือ "ส้ม" และ "น้ำเงิน" ในทางที่เป็นทางการ เราจะอธิบายชุดข้อมูล $D$ ดังนี้
where:
- $x_i$ คือค่าของฟีเจอร์ตัวเลขใน $\mathbb{R}$ (ชุดของจำนวนจริง)
- $y_i$ คือค่าป้ายกำกับการแยกประเภทแบบไบนารีใน {orange, blue}
วัตถุประสงค์ของเราคือการหาค่าเกณฑ์ $t$ (เกณฑ์) ที่ทำให้การแบ่งตัวอย่าง $D$ เป็นกลุ่ม $T(rue)$ และ $F(alse)$ ตามเงื่อนไข $x_i \geq t$ ปรับปรุงการแยกป้ายกำกับได้ เช่น ตัวอย่าง "สีส้ม" ในกลุ่ม $T$ มากขึ้นและตัวอย่าง "สีน้ำเงิน" ในกลุ่ม $F$ มากขึ้น
เอนโทรปีของ Shannon เป็นมาตรวัดความไม่เป็นระเบียบ สําหรับป้ายกำกับแบบไบนารี
- เอนโทรปีของ Shannon จะสูงสุดเมื่อป้ายกำกับในตัวอย่างมีความสมดุล (สีน้ำเงิน 50% และสีส้ม 50%)
- เอนโทรปีของ Shannon จะต่ำสุด (ค่า 0) เมื่อป้ายกำกับในตัวอย่างเป็นสีเดียว (น้ำเงิน 100% หรือส้ม 100%)
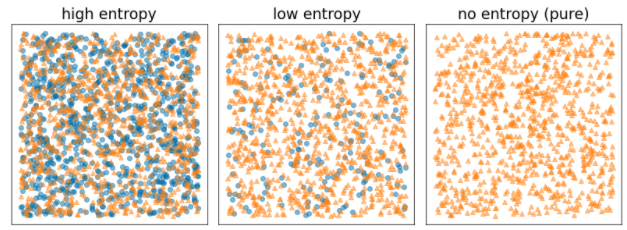
รูปที่ 8 ระดับเอนโทรปี 3 ระดับ
ในทางที่เป็นทางการ เราต้องการค้นหาเงื่อนไขที่จะลดผลรวมถ่วงน้ำหนักของการเข้ารหัสของข้อมูลการแจกแจงป้ายกำกับใน $T$ และ $F$ คะแนนที่เกี่ยวข้องคือการได้ข้อมูล ซึ่งเป็นความแตกต่างระหว่างการเข้ารหัสของข้อมูล $D$ กับการเข้ารหัสของข้อมูล {$T$,$F$} ความแตกต่างนี้เรียกว่าการได้ข้อมูล
รูปภาพต่อไปนี้แสดงการแยกที่ไม่ดี ซึ่งเอนโทรปียังคงสูงและค่าการได้ข้อมูลต่ำ
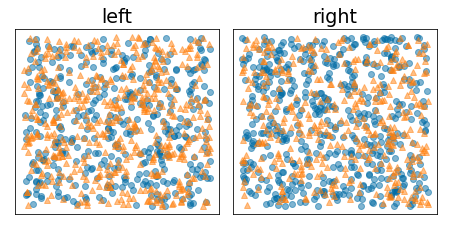
รูปที่ 9 การแยกที่ไม่ถูกต้องจะไม่ลดเอนโทรปีของป้ายกำกับ
ในทางตรงกันข้าม รูปภาพต่อไปนี้แสดงการแยกที่ดีกว่าซึ่งเอนโทรปีจะต่ำ (และอัตราขยายข้อมูลสูง)
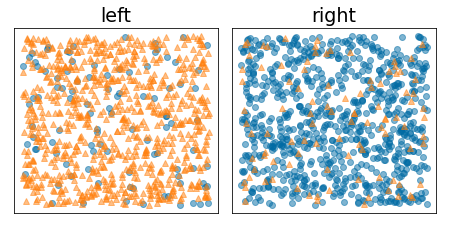
รูปที่ 10 การแยกที่ดีจะช่วยลดความผันผวนของป้ายกำกับ
อย่างเป็นทางการ
\[\begin{eqnarray} T & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \ge t \} \\[12pt] F & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \lt t \} \\[12pt] R(X) & = & \frac{\lvert \{ x | x \in X \ \textrm{and} \ x = \mathrm{pos} \} \rvert}{\lvert X \rvert} \\[12pt] H(X) & = & - p \log p - (1 - p) \log (1-p) \ \textrm{with} \ p = R(X)\\[12pt] IG(D,T,F) & = & H(D) - \frac {\lvert T\rvert} {\lvert D \rvert } H(T) - \frac {\lvert F \rvert} {\lvert D \rvert } H(F) \end{eqnarray}\]
where:
- $IG(D,T,F)$ คืออัตราส่วนการได้ข้อมูลจากการแยก $D$ เป็น $T$ และ $F$
- $H(X)$ คือเอนโทรปีของชุดตัวอย่าง $X$
- $|X|$ คือจํานวนองค์ประกอบในเซต $X$
- $t$ คือค่าเกณฑ์
- $pos$ คือค่าป้ายกํากับบวก เช่น "blue" ในตัวอย่างข้างต้น การเลือกป้ายกำกับอื่นเป็น "ป้ายกำกับบวก" จะไม่เปลี่ยนแปลงค่าของข้อมูลความผันผวนหรืออัตราขยายข้อมูล
- $R(X)$ คืออัตราส่วนของค่าป้ายกำกับบวกในตัวอย่าง $X$
- $D$ คือชุดข้อมูล (ตามที่ระบุไว้ก่อนหน้านี้ในหน่วยนี้)
ในตัวอย่างต่อไปนี้ เราจะพิจารณาชุดข้อมูลการจัดประเภทแบบ 2 กลุ่มที่มีฟีเจอร์ตัวเลขรายการเดียว $x$ รูปภาพต่อไปนี้แสดงค่าเกณฑ์ $t$ (แกน x) ที่ต่างกัน
- ฮิสโตแกรมของฟีเจอร์ $x$
- อัตราส่วนของตัวอย่าง "สีน้ำเงิน" ในชุด $D$, $T$ และ $F$ ตามค่าเกณฑ์
- เอนโทรปีใน $D$, $T$ และ $F$
- อัตราผลตอบแทนของข้อมูล ซึ่งก็คือเดลต้าเอนโทรปีระหว่าง $D$ กับ {$T$,$F$} ที่ถ่วงน้ำหนักด้วยจำนวนตัวอย่าง
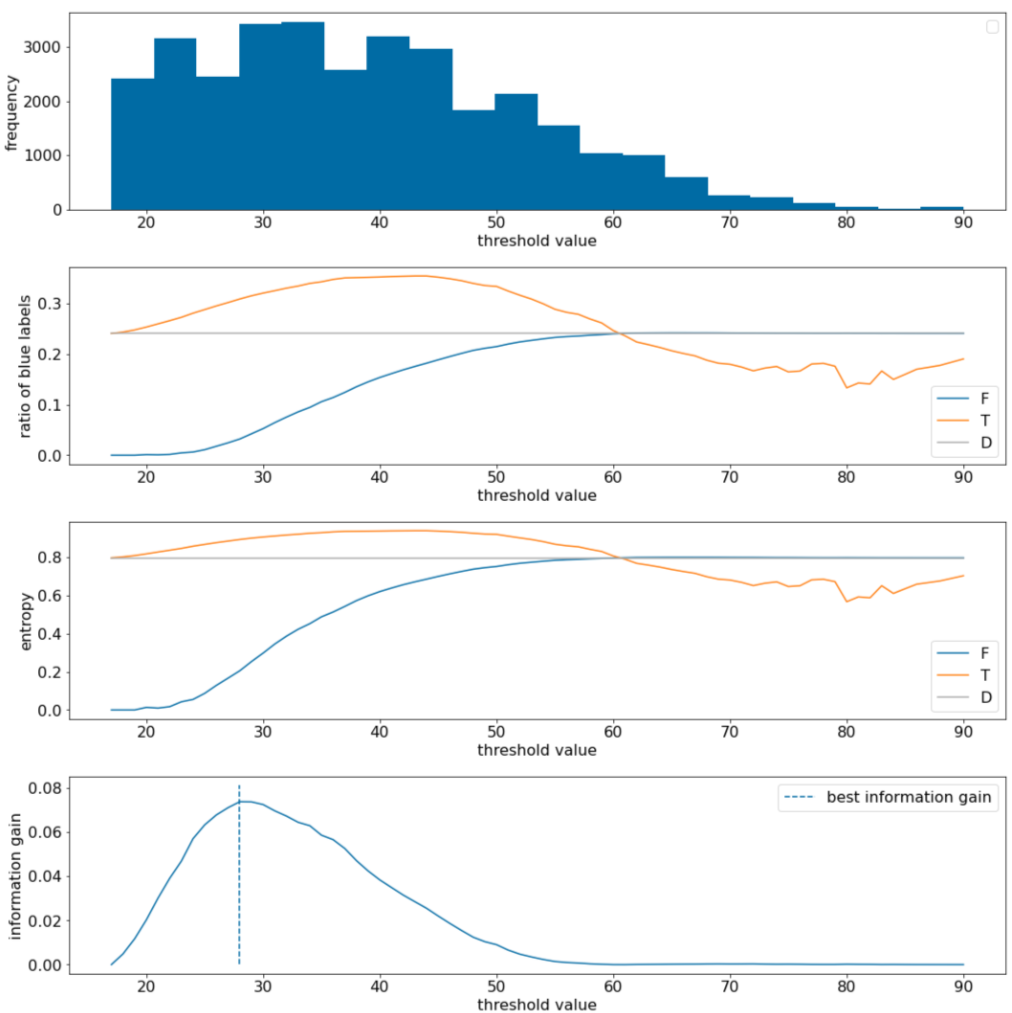
รูปที่ 11 ผังเกณฑ์ 4 รายการ
ผังเหล่านี้แสดงข้อมูลต่อไปนี้
- ผัง "ความถี่" แสดงให้เห็นว่าค่าที่สังเกตได้ค่อนข้างกระจายตัวดี โดยมีค่าเข้มข้นระหว่าง 18 ถึง 60 ค่าที่กระจายกว้างหมายความว่ามีโอกาสแยกกลุ่มได้หลายกลุ่ม ซึ่งเหมาะสำหรับการฝึกโมเดล
อัตราส่วนของป้ายกำกับ "สีน้ำเงิน" ในชุดข้อมูลคือประมาณ 25% ผัง "อัตราส่วนของป้ายกํากับสีน้ำเงิน" แสดงให้เห็นว่าสําหรับค่าเกณฑ์ระหว่าง 20 ถึง 50
- ชุด $T$ มีตัวอย่างป้ายกำกับ "น้ำเงิน" มากเกินไป (สูงสุด 35% สำหรับเกณฑ์ 35)
- ชุด $F$ มีค่าขาดทุนเสริมของตัวอย่างป้ายกำกับ "สีน้ำเงิน" (เพียง 8% สำหรับเกณฑ์ 35)
ทั้งผัง "อัตราส่วนของป้ายกำกับสีน้ำเงิน" และ "ความผันผวนของข้อมูล" บ่งชี้ว่าป้ายกำกับสามารถแยกออกจากกันได้ค่อนข้างดีในช่วงเกณฑ์นี้
การสังเกตนี้ได้รับการยืนยันในผัง "การได้ข้อมูล" เราพบว่าค่า t ที่ให้ค่าความได้เปรียบด้านข้อมูลสูงสุดคือ t~=28 โดยมีค่าความได้เปรียบด้านข้อมูลประมาณ 0.074 ดังนั้นเงื่อนไขที่ตัวแยกแสดงผลจะเป็น $x \geq 28$
ผลที่ได้คือค่าบวกหรือค่าว่างเสมอ ค่านี้จะเข้าใกล้ 0 เมื่อค่าเกณฑ์เข้าใกล้ค่าสูงสุด / ต่ำสุด ในกรณีเหล่านี้ ข้อมูล $F$ หรือ $T$ จะว่างเปล่า ขณะที่อีกข้อมูลหนึ่งมีชุดข้อมูลทั้งหมดและแสดงเอนโทรปีเท่ากับใน $D$ อัตราส่วนของป้ายกำกับ "สีน้ำเงิน" สำหรับทั้ง $T$ และ $F$ จะเหมือนกับของ $D$ และอัตราส่วนการได้ข้อมูลจะเป็น 0
ค่าที่เป็นไปได้สำหรับ $t$ ในชุดจำนวนจริง ($\mathbb{R}$) มีจำนวนอนันต์ อย่างไรก็ตาม เมื่อพิจารณาตัวอย่างที่มีจำนวนจำกัด การแบ่ง $D$ เป็น $T$ และ $F$ จะมีเพียงจำนวนจำกัดเท่านั้น ดังนั้น ค่าของ $t$ ที่มีความหมายในการทดสอบจึงมีเพียงจำนวนจำกัด
แนวทางแบบคลาสสิกคือการจัดเรียงค่า xi ตามลําดับจากน้อยไปมาก xs(i) โดยที่
จากนั้นทดสอบ $t$ สำหรับทุกค่าที่อยู่ระหว่างค่าที่เรียงลําดับกันของ $x_i$ ตัวอย่างเช่น สมมติว่าคุณมีค่าทศนิยม 1,000 ค่าของฟีเจอร์หนึ่งๆ หลังจากจัดเรียงแล้ว สมมติว่า 2 ค่าแรกคือ 8.5 และ 8.7 ในกรณีนี้ ค่าเกณฑ์แรกที่จะทดสอบคือ 8.6
ในทางที่เป็นทางการ เราจะพิจารณาค่าต่อไปนี้สำหรับ t
ความซับซ้อนของเวลาของอัลกอริทึมนี้คือ $\mathcal{O} ( n \log n) $ โดยที่ $n$ คือจำนวนตัวอย่างในโหนด (เนื่องจากการจัดเรียงค่าฟีเจอร์) เมื่อใช้กับต้นไม้การตัดสินใจ ระบบจะใช้อัลกอริทึมตัวแยกกับโหนดและฟีเจอร์แต่ละรายการ โปรดทราบว่าโหนดแต่ละโหนดจะได้รับตัวอย่างประมาณ 1/2 ของโหนดหลัก ดังนั้น ตามความซับซ้อนของเวลาในการฝึกต้นไม้การตัดสินใจด้วยตัวแยกนี้ตามทฤษฎีหลักจะเท่ากับ
where:
- $m$ คือจํานวนฟีเจอร์
- $n$ คือจํานวนตัวอย่างการฝึก
ในอัลกอริทึมนี้ ค่าของฟีเจอร์ไม่สำคัญ มีเพียงลําดับเท่านั้นที่ส่งผล ด้วยเหตุนี้ อัลกอริทึมนี้จึงทํางานโดยไม่ขึ้นกับมาตราส่วนหรือการกระจายของค่าฟีเจอร์ ด้วยเหตุนี้ เราจึงไม่จำเป็นต้องทำให้เป็นมาตรฐานหรือปรับขนาดฟีเจอร์ที่เป็นตัวเลขเมื่อฝึกต้นไม้การตัดสินใจ