সংখ্যাসূচক বৈশিষ্ট্য সহ বাইনারি শ্রেণীবিভাগের জন্য সঠিক স্প্লিটার,সংখ্যাসূচক বৈশিষ্ট্য সহ বাইনারি শ্রেণীবিভাগের জন্য সঠিক স্প্লিটার

এই ইউনিটে, আপনি সবচেয়ে সহজ এবং সবচেয়ে সাধারণ স্প্লিটার অ্যালগরিদমটি অন্বেষণ করবেন, যা নিম্নলিখিত সেটিংসে $\mathrm{feature}_i \geq t$ ফর্মের শর্ত তৈরি করে:

• বাইনারি ক্লাসিফিকেশন টাস্ক
• উদাহরণে মান অনুপস্থিত ছাড়া
• উদাহরণগুলিতে পূর্বনির্ধারিত সূচক ছাড়াই

একটি সংখ্যাসূচক বৈশিষ্ট্য এবং একটি বাইনারি লেবেল "কমলা" এবং "নীল" সহ $n$ উদাহরণগুলির একটি সেট অনুমান করুন। আনুষ্ঠানিকভাবে, আসুন ডেটাসেট $D$কে এভাবে বর্ণনা করি:

$$D = \{(x_i,y_i)\}_{i\in[1,n]}$$

কোথায়:

• $x_i$ হল $\mathbb{R}$ (বাস্তব সংখ্যার সেট) এ একটি সংখ্যাসূচক বৈশিষ্ট্যের মান।
• $y_i$ হল একটি বাইনারি শ্রেণীবিভাগ লেবেল মান {কমলা, নীল}।

আমাদের উদ্দেশ্য হল একটি থ্রেশহোল্ড মান $t$ (থ্রেশহোল্ড) খুঁজে বের করা যাতে উদাহরণ $D$কে $T(rue)$ এবং $F(alse)$ গ্রুপে ভাগ করলে $x_i \geq t$ অবস্থার উন্নতি হয় লেবেল বিচ্ছেদ; উদাহরণস্বরূপ, $T$-এ আরও "কমলা" উদাহরণ এবং $F$-এ আরও "নীল" উদাহরণ।

শ্যানন এনট্রপি ব্যাধির একটি পরিমাপ। একটি বাইনারি লেবেলের জন্য:

• শ্যানন এনট্রপি সর্বাধিক হয় যখন উদাহরণগুলির লেবেলগুলি সুষম থাকে (50% নীল এবং 50% কমলা)।
• শ্যানন এনট্রপি ন্যূনতম (মান শূন্য) হয় যখন উদাহরণগুলির লেবেলগুলি খাঁটি হয় (100% নীল বা 100% কমলা)।

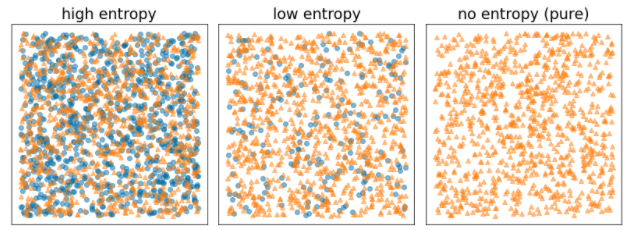
চিত্র 8. তিনটি ভিন্ন এনট্রপি স্তর।

আনুষ্ঠানিকভাবে, আমরা এমন একটি শর্ত খুঁজে পেতে চাই যা $T$ এবং $F$ এ লেবেল বিতরণের এনট্রপির ওজনযুক্ত যোগফলকে হ্রাস করে। সংশ্লিষ্ট স্কোর হল তথ্য লাভ , যা $D$ এর এনট্রপি এবং {$T$,$F$} এনট্রপির মধ্যে পার্থক্য। এই পার্থক্যকে বলা হয় তথ্য লাভ ।

নিম্নলিখিত চিত্রটি একটি খারাপ বিভাজন দেখায়, যেখানে এনট্রপি বেশি থাকে এবং তথ্য কম হয়:

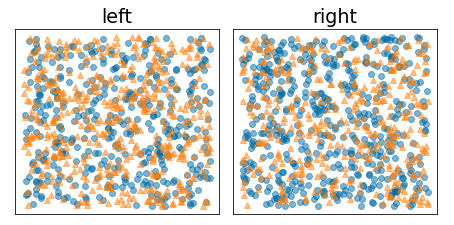
চিত্র 9. একটি খারাপ বিভাজন লেবেলের এনট্রপি হ্রাস করে না।

বিপরীতে, নিম্নলিখিত চিত্রটি একটি ভাল বিভাজন দেখায় যেখানে এনট্রপি কম হয়ে যায় (এবং তথ্য বেশি হয়):

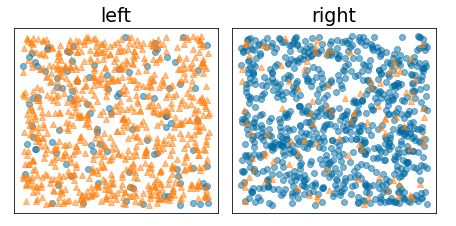
চিত্র 10. একটি ভাল বিভাজন লেবেলের এনট্রপি হ্রাস করে।

আনুষ্ঠানিকভাবে:

\[\begin{eqnarray} T & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \ge t \} \\[12pt] F & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \lt t \} \\[12pt] R(X) & = & \frac{\lvert \{ x | x \in X \ \textrm{and} \ x = \mathrm{pos} \} \rvert}{\lvert X \rvert} \\[12pt] H(X) & = & - p \log p - (1 - p) \log (1-p) \ \textrm{with} \ p = R(X)\\[12pt] IG(D,T,F) & = & H(D) - \frac {\lvert T\rvert} {\lvert D \rvert } H(T) - \frac {\lvert F \rvert} {\lvert D \rvert } H(F) \end{eqnarray}\]

কোথায়:

• $IG(D,T,F)$ হল $D$কে $T$ এবং $F$ এ বিভক্ত করার তথ্য লাভ।
• $H(X)$ হল $X$ উদাহরণের সেটের এনট্রপি।
• $|X|$ হল $X$ সেটের উপাদানের সংখ্যা।
• $t$ হল থ্রেশহোল্ড মান।
• $pos$ হল ইতিবাচক লেবেল মান, উদাহরণস্বরূপ, উপরের উদাহরণে "নীল"। "ইতিবাচক লেবেল" হতে একটি ভিন্ন লেবেল বাছাই করা এনট্রপি বা তথ্য লাভের মান পরিবর্তন করে না।
• $R(X)$ হল $X$ উদাহরণে ইতিবাচক লেবেল মানের অনুপাত।
• $D$ হল ডেটাসেট (যেমন এই ইউনিটে আগে সংজ্ঞায়িত করা হয়েছে)।

নিম্নলিখিত উদাহরণে, আমরা একটি একক সংখ্যাসূচক বৈশিষ্ট্য $x$ সহ একটি বাইনারি শ্রেণীবিভাগ ডেটাসেট বিবেচনা করি। নিম্নলিখিত চিত্রটি বিভিন্ন থ্রেশহোল্ড $t$ মানের (x-অক্ষ) জন্য দেখায়:

1. $x$ বৈশিষ্ট্যটির হিস্টোগ্রাম।
2. থ্রেশহোল্ড মান অনুযায়ী $D$, $T$, এবং $F$ সেটে "নীল" উদাহরণের অনুপাত।
3. $D$, $T$ এবং $F$ এ এনট্রপি।
4. তথ্য লাভ; অর্থাৎ, $D$ এবং {$T$,$F$} এর মধ্যে এনট্রপি ডেল্টা উদাহরণের সংখ্যা দ্বারা ওজন করা হয়েছে।

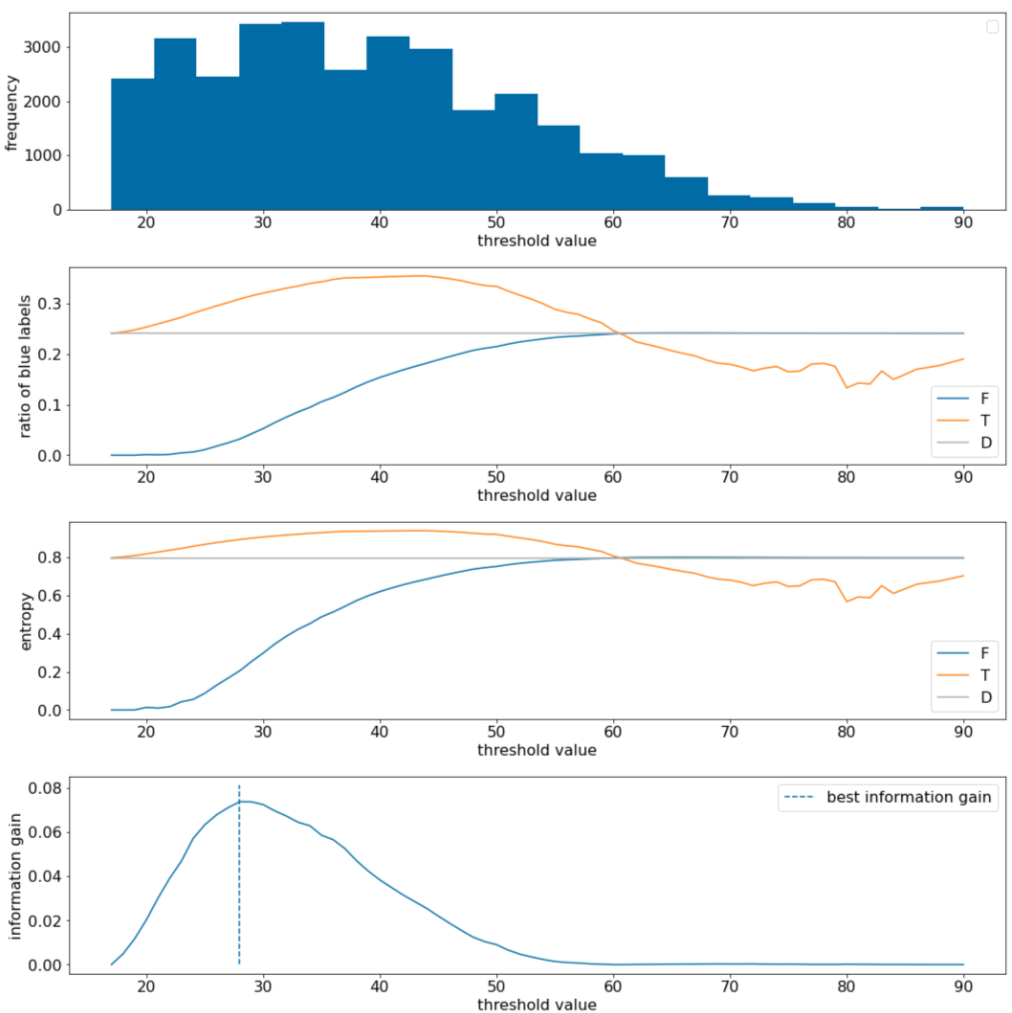
চিত্র 11. চার প্রান্তিক প্লট।

এই প্লটগুলি নিম্নলিখিতগুলি দেখায়:

• "ফ্রিকোয়েন্সি" প্লটটি দেখায় যে পর্যবেক্ষণগুলি 18 এবং 60 এর মধ্যে ঘনত্বের সাথে তুলনামূলকভাবে ভালভাবে ছড়িয়ে পড়েছে। একটি বিস্তৃত মূল্যের স্প্রেডের অর্থ হল প্রচুর সম্ভাব্য বিভাজন রয়েছে, যা মডেলটিকে প্রশিক্ষণের জন্য ভাল।

• ডেটাসেটে "নীল" লেবেলের অনুপাত হল ~25%৷ "নীল লেবেলের অনুপাত" প্লট দেখায় যে 20 এবং 50 এর মধ্যে থ্রেশহোল্ড মানগুলির জন্য:

  • $T$ সেটটিতে অতিরিক্ত "নীল" লেবেলের উদাহরণ রয়েছে (থ্রেশহোল্ড 35 এর জন্য 35% পর্যন্ত)।
  • $F$ সেটে "নীল" লেবেলের উদাহরণগুলির পরিপূরক ঘাটতি রয়েছে (থ্রেশহোল্ড 35 এর জন্য শুধুমাত্র 8%)।

  "নীল লেবেলের অনুপাত" এবং "এনট্রপি" প্লট উভয়ই ইঙ্গিত দেয় যে লেবেলগুলি এই প্রান্তিক পরিসরে তুলনামূলকভাবে ভালভাবে আলাদা করা যেতে পারে।

• এই পর্যবেক্ষণটি "তথ্য লাভ" প্লটে নিশ্চিত করা হয়েছে। আমরা দেখতে পাই যে ~0.074 একটি তথ্য লাভের মানের জন্য t~=28 দিয়ে সর্বাধিক তথ্য লাভ পাওয়া যায়। অতএব, স্প্লিটার দ্বারা প্রত্যাবর্তিত শর্তটি হবে $x \geq 28$।

• তথ্য লাভ সবসময় ইতিবাচক বা শূন্য হয়। থ্রেশহোল্ড মান তার সর্বোচ্চ / সর্বনিম্ন মানের দিকে রূপান্তরিত হওয়ার সাথে সাথে এটি শূন্যে রূপান্তরিত হয়। এই ক্ষেত্রে, হয় $F$ বা $T$ খালি হয়ে যায় যখন অন্যটিতে পুরো ডেটাসেট থাকে এবং $D$-এর সমান একটি এনট্রপি দেখায়। তথ্য লাভ শূন্য হতে পারে যখন $H(T)$ = $H(F)$ = $H(D)$। থ্রেশহোল্ড 60-এ, $T$ এবং $F$ উভয়ের জন্য "নীল" লেবেলের অনুপাত $D$-এর সমান এবং তথ্য লাভ শূন্য৷

প্রকৃত সংখ্যার ($\mathbb{R}$) সেটে $t$-এর প্রার্থীর মান অসীম। যাইহোক, সসীম সংখ্যক উদাহরণ দিলে, $D$-এর $T$ এবং $F$-এ শুধুমাত্র একটি সীমিত সংখ্যক বিভাজন বিদ্যমান। অতএব, শুধুমাত্র $t$ এর একটি সীমিত সংখ্যক মান পরীক্ষা করার জন্য অর্থপূর্ণ।

একটি শাস্ত্রীয় পদ্ধতি হল x _i মানগুলিকে x _s(i) ক্রমবর্ধমান ক্রমে সাজানো যেমন:

$$ x_{s(i)} \leq x_{s(i+1)} $$

তারপর, পরপর বাছাই করা $x_i$ এর মধ্যে প্রতিটি মানের জন্য $t$ পরীক্ষা করুন। উদাহরণস্বরূপ, ধরুন আপনার কাছে একটি নির্দিষ্ট বৈশিষ্ট্যের 1,000 ফ্লোটিং-পয়েন্ট মান রয়েছে। সাজানোর পর, ধরুন প্রথম দুটি মান হল 8.5 এবং 8.7। এই ক্ষেত্রে, পরীক্ষা করার প্রথম থ্রেশহোল্ড মান হবে 8.6।

আনুষ্ঠানিকভাবে, আমরা t এর জন্য নিম্নলিখিত প্রার্থীর মানগুলি বিবেচনা করি:

$$ X = \left\{ \frac {x_{s(i)} + x_{s(i + 1)}} {2} \lvert x_{s(i)} \ne x_{s(i+1)} \right\} $$

এই অ্যালগরিদমের সময় জটিলতা হল $\mathcal{O} ( n \log n) $ $n$ সহ নোডের উদাহরণের সংখ্যা (বৈশিষ্ট্যের মানগুলি সাজানোর কারণে)। সিদ্ধান্ত গাছে প্রয়োগ করা হলে, স্প্লিটার অ্যালগরিদম প্রতিটি নোড এবং প্রতিটি বৈশিষ্ট্যে প্রয়োগ করা হয়। মনে রাখবেন যে প্রতিটি নোড তার মূল উদাহরণগুলির ~1/2 গ্রহণ করে। অতএব, মাস্টার থিওরেম অনুসারে, এই স্প্লিটার দিয়ে একটি সিদ্ধান্ত গাছকে প্রশিক্ষণের সময় জটিলতা হল:

$$ \mathcal{O} ( m n \log^2 n ) $$

কোথায়:

• $m$ হল বৈশিষ্ট্যের সংখ্যা।
• $n$ হল প্রশিক্ষণের উদাহরণের সংখ্যা।

এই অ্যালগরিদমে, বৈশিষ্ট্যের মান কোন ব্যাপার না; শুধুমাত্র আদেশ গুরুত্বপূর্ণ। এই কারণে, এই অ্যালগরিদম স্কেল বা বৈশিষ্ট্য মান বিতরণ স্বাধীনভাবে কাজ করে। এই কারণেই একটি সিদ্ধান্ত গাছকে প্রশিক্ষণ দেওয়ার সময় আমাদের সংখ্যাসূচক বৈশিষ্ট্যগুলিকে স্বাভাবিক করার বা স্কেল করার দরকার নেই।