В этом модуле вы изучите простейший и наиболее распространенный алгоритм разделения, который создает условия вида $\mathrm{feature}_i \geq t$ в следующих настройках:
- Задача двоичной классификации
- Без пропущенных значений в примерах
- Без заранее вычисленного индекса в примерах
Предположим, имеется набор из $n$ примеров с числовым признаком и двоичной меткой «оранжевый» и «синий». Формально опишем набор данных $D$ как:
где:
- $x_i$ — значение числового признака в $\mathbb{R}$ (множестве действительных чисел).
- $y_i$ — значение метки двоичной классификации в {оранжевом, синем} цвете.
Наша цель — найти такое пороговое значение $t$ (порог), при котором разделение примеров $D$ на группы $T(rue)$ и $F(alse)$ по условию $x_i \geq t$ улучшает разделение меток; например, больше «оранжевых» примеров в $T$ и больше «синих» примеров в $F$.
Энтропия Шеннона является мерой беспорядка. Для двоичной метки:
- Энтропия Шеннона максимальна, когда метки в примерах сбалансированы (50% синего и 50% оранжевого).
- Энтропия Шеннона минимальна (значение 0), когда метки в примерах чистые (100% синие или 100% оранжевые).
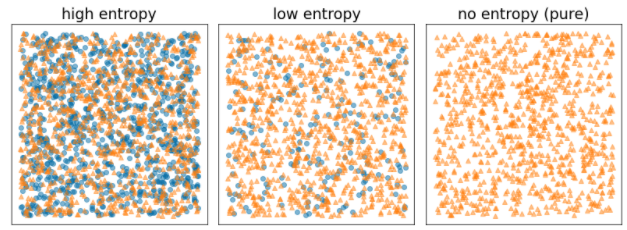
Рисунок 8. Три разных уровня энтропии.
Формально мы хотим найти условие, уменьшающее взвешенную сумму энтропии распределений меток в $T$ и $F$. Соответствующая оценка — это прирост информации , который представляет собой разницу между энтропией $D$ и энтропией {$T$,$F$}. Эта разница называется приростом информации .
На следующем рисунке показано плохое разделение, при котором энтропия остается высокой, а прирост информации – низким:
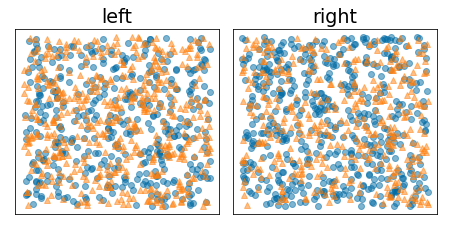
Рисунок 9. Плохое разделение не снижает энтропию метки.
Напротив, на следующем рисунке показано лучшее разделение, при котором энтропия становится низкой (а прирост информации высок):
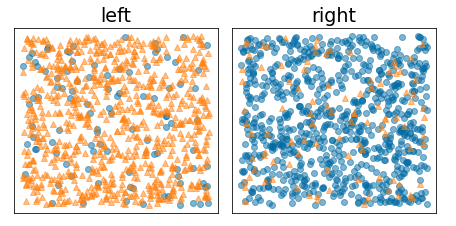
Рисунок 10. Хорошее разделение снижает энтропию метки.
Формально:
\[\begin{eqnarray} T & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \ge t \} \\[12pt] F & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \lt t \} \\[12pt] R(X) & = & \frac{\lvert \{ x | x \in X \ \textrm{and} \ x = \mathrm{pos} \} \rvert}{\lvert X \rvert} \\[12pt] H(X) & = & - p \log p - (1 - p) \log (1-p) \ \textrm{with} \ p = R(X)\\[12pt] IG(D,T,F) & = & H(D) - \frac {\lvert T\rvert} {\lvert D \rvert } H(T) - \frac {\lvert F \rvert} {\lvert D \rvert } H(F) \end{eqnarray}\]
где:
- $IG(D,T,F)$ — это информационный выигрыш от разделения $D$ на $T$ и $F$.
- $H(X)$ — энтропия множества примеров $X$.
- $|X|$ — количество элементов в множестве $X$.
- $t$ — пороговое значение.
- $pos$ — это положительное значение метки, например «синий» в приведенном выше примере. Выбор другой метки в качестве «положительной метки» не меняет значения энтропии или прироста информации.
- $R(X)$ — соотношение положительных значений меток в примерах $X$.
- $D$ — это набор данных (как определено ранее в этом модуле).
В следующем примере мы рассматриваем набор данных двоичной классификации с одним числовым признаком $x$. На следующем рисунке показаны различные пороговые значения $t$ (ось X):
- Гистограмма признака $x$.
- Соотношение «синих» примеров в $D$, $T$ и $F$ устанавливается в соответствии с пороговым значением.
- Энтропия в $D$, $T$ и $F$.
- Прирост информации; то есть дельта энтропии между $D$ и {$T$,$F$}, взвешенная по количеству примеров.
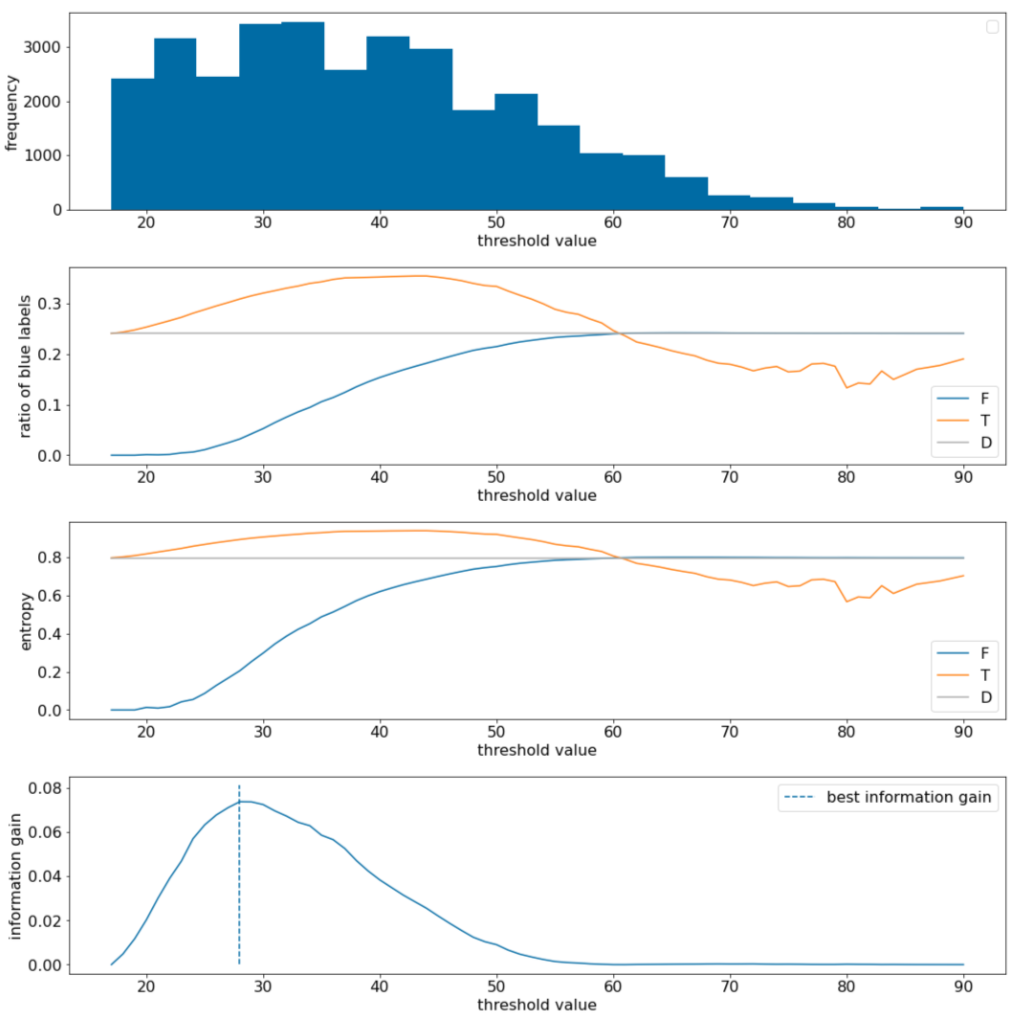
Рисунок 11. Четыре пороговых графика.
Эти графики показывают следующее:
- График «частоты» показывает, что наблюдения относительно хорошо разбросаны с концентрациями от 18 до 60. Широкий разброс значений означает, что существует много потенциальных разделений, что хорошо для обучения модели.
Доля «синих» меток в наборе данных составляет ~25%. График «коэффициента синей метки» показывает, что для пороговых значений от 20 до 50:
- Набор $T$ содержит избыток примеров «синих» меток (до 35% для порога 35).
- Набор $F$ содержит дополнительный дефицит примеров «синих» меток (всего 8% для порога 35).
Как «соотношение синих меток», так и графики «энтропии» показывают, что метки могут быть относительно хорошо разделены в этом пороговом диапазоне.
Это наблюдение подтверждается графиком «прироста информации». Мы видим, что максимальный прирост информации достигается при t~=28 при значении прироста информации ~0,074. Следовательно, условие, возвращаемое разделителем, будет $x \geq 28$.
Прирост информации всегда положителен или равен нулю. Он сходится к нулю, когда пороговое значение приближается к своему максимальному/минимальному значению. В этих случаях либо $F$, либо $T$ становится пустым, а другой содержит весь набор данных и показывает энтропию, равную энтропии в $D$. Прирост информации также может быть нулевым, когда $H(T)$ = $H(F)$ = $H(D)$. На пороге 60 соотношение «синих» меток как для $T$, так и для $F$ такое же, как и для $D$, и прирост информации равен нулю.
Возможные значения $t$ в множестве действительных чисел ($\mathbb{R}$) бесконечны. Однако при конечном числе примеров существует лишь конечное число делений $D$ на $T$ и $F$. Следовательно, только конечное число значений $t$ имеет смысл проверять.
Классический подход заключается в сортировке значений x i в порядке возрастания x s(i) так, чтобы:
Затем проверьте $t$ для каждого значения на полпути между последовательными отсортированными значениями $x_i$. Например, предположим, что у вас есть 1000 значений с плавающей запятой для определенного объекта. Предположим, что после сортировки первые два значения равны 8,5 и 8,7. В этом случае первое пороговое значение для проверки будет 8,6.
Формально мы рассматриваем следующие возможные значения t:
Временная сложность этого алгоритма составляет $\mathcal{O} ( n \log n) $ с $n$ количеством примеров в узле (из-за сортировки значений признаков). При применении к дереву решений алгоритм разделения применяется к каждому узлу и каждому объекту. Обратите внимание, что каждый узел получает ~1/2 своих родительских примеров. Следовательно, согласно основной теореме , временная сложность обучения дерева решений с помощью этого сплиттера равна:
где:
- $m$ — количество функций.
- $n$ — количество обучающих примеров.
В этом алгоритме ценность признаков не имеет значения; важен только порядок. По этой причине этот алгоритм работает независимо от масштаба или распределения значений признаков. Вот почему нам не нужно нормализовать или масштабировать числовые характеристики при обучении дерева решений.
