Bộ chia chính xác để phân loại nhị phân với các tính năng dạng số

Trong bài này, bạn sẽ tìm hiểu thuật toán phân chia phổ biến và đơn giản nhất. Thuật toán này sẽ tạo các điều kiện của biểu mẫu $\mathrm{feature}_i \geq t$ trong chế độ cài đặt sau:

• Nhiệm vụ phân loại tệp nhị phân
• Không có giá trị nào trong các ví dụ
• Không có chỉ mục được tính toán trước trong các ví dụ

Giả sử một tập hợp các ví dụ $n$ với một tính năng dạng số và nhãn nhị phân &"cam" và "blue" Chính thức, hãy mô tả tập dữ liệu $D$ như sau:

$$D = \{(x_i,y_i)\}_{i\in[1,n]}$$

nơi:

• $x_i$ là giá trị của một tính năng số trong $\mathbb{R}$ (tập hợp các số thực).
• $y_i$ là giá trị của nhãn phân loại nhị phân trong {cam, xanh}.

Mục tiêu của chúng tôi là tìm ngưỡng giá trị $t$ (ngưỡng) chia các ví dụ $D$ vào các nhóm $T(rue)$ và $F(alse)$ theo điều kiện $x_i \geq t$ để cải thiện sự tách biệt các nhãn; ví dụ: more "Orange" ví dụ trong $T$ và các trường hợp khác "blue"

Ehannon entropy là một giải pháp đo lường chứng rối loạn. Đối với nhãn nhị phân:

• Entropy của Shannon đạt mức tối đa khi các nhãn trong các ví dụ được cân bằng (50% màu xanh dương và 50% màu cam).
• Entropy của Shannon ở mức tối thiểu (giá trị bằng 0) khi các nhãn trong ví dụ là tinh khiết (100% màu xanh lam hoặc 100% màu cam).

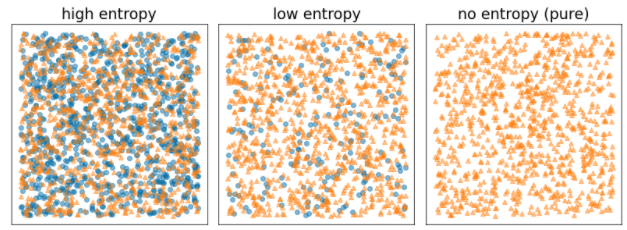
Hình 8. Ba cấp độ entropy khác nhau.

 

Chính thức, chúng ta muốn tìm một điều kiện làm giảm tổng trọng số của entropy của sự phân phối nhãn trong $T$ và $F$. Điểm tương ứng là mức tăng thông tin, là sự khác biệt giữa entropy $D$&39; {$T$,$F$}. Sự khác biệt này được gọi là mức tăng thông tin.

Hình dưới đây cho thấy phần phân tách không hợp lệ, trong đó entropy vẫn cao và thông tin tăng lên thấp:

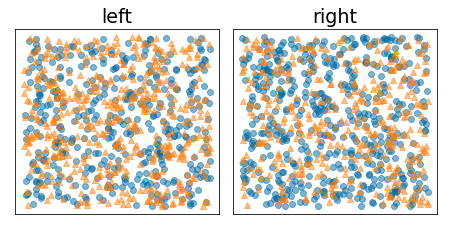
Hình 9. Việc phân tách không hợp lệ sẽ không làm giảm entropy của nhãn.

 

Ngược lại, hình sau đây cho thấy mức phân tách tốt hơn, trong đó entropy trở nên thấp (và thông tin tăng cao):

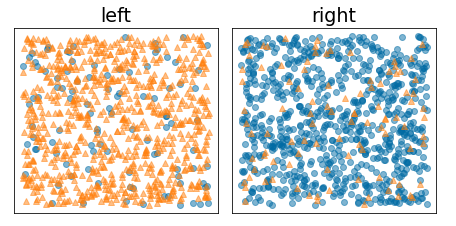
Hình 10. Việc phân tách hiệu quả sẽ làm giảm entropy của nhãn.

 

Chính thức:

\[\begin{eqnarray} T & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \ge t \} \\[12pt] F & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \lt t \} \\[12pt] R(X) & = & \frac{\lvert \{ x | x \in X \ \textrm{and} \ x = \mathrm{pos} \} \rvert}{\lvert X \rvert} \\[12pt] H(X) & = & - p \log p - (1 - p) \log (1-p) \ \textrm{with} \ p = R(X)\\[12pt] IG(D,T,F) & = & H(D) - \frac {\lvert T\rvert} {\lvert D \rvert } H(T) - \frac {\lvert F \rvert} {\lvert D \rvert } H(F) \end{eqnarray}\]

nơi:

• $IG(D,T,F)$ là mức tăng thông tin khi chia $D$ thành $T$ và $F$.
• $H(X)$ là giá trị entropy của tập hợp ví dụ $X$.
• $|X|$ là số phần tử trong tập hợp $X$.
• $t$ là giá trị ngưỡng.
• $pos$ là giá trị nhãn tích cực, ví dụ: "blue" trong ví dụ ở trên. Việc chọn một nhãn khác làm "nhãn tích cực" không thay đổi giá trị của entropy hoặc việc lấy thông tin.
• $R(X)$ là tỷ lệ giá trị nhãn dương trong ví dụ $X$.
• $D$ là tập dữ liệu (như đã định nghĩa trong bài này).

Trong ví dụ sau, chúng tôi xem xét một tập dữ liệu phân loại nhị phân có một tính năng số duy nhất $x$. Hình bên dưới cho thấy các giá trị ngưỡng $t$ khác nhau (Trục x):

1. Biểu đồ của tính năng $x$.
2. Tỷ lệ "blue" ví dụ trong các tập hợp $D$, $T$ và $F$ theo giá trị ngưỡng.
3. Entropy trong $D$, $T$ và $F$.
4. Giá trị thu được thông tin; nghĩa là entropy delta giữa $D$ và {$T$,$F$} được tính trọng số theo số lượng ví dụ.

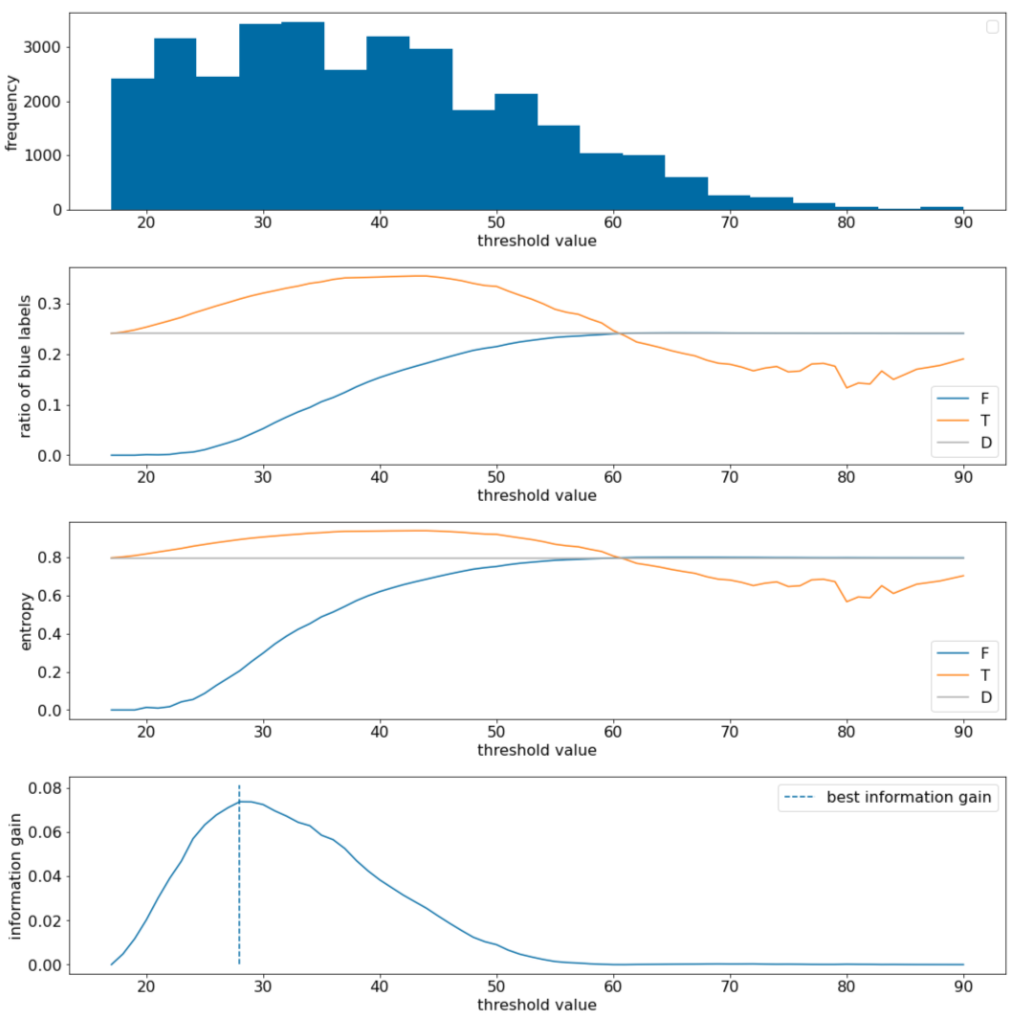
Hình 11. 4 biểu đồ ngưỡng.

 

Những biểu đồ này cho thấy những điều sau:

• "frequency" cốt truyện cho thấy rằng các quan sát tương đối tốt với độ tập trung trong khoảng từ 18 đến 60. Sự chênh lệch giá trị rộng có nghĩa là có rất nhiều yếu tố có thể phân tách, vì vậy, rất phù hợp để đào tạo mô hình.

• Tỷ lệ "blue" nhãn trong tập dữ liệu là ~25%. "tỷ lệ nhãn màu xanh" biểu đồ cho thấy rằng đối với các giá trị ngưỡng từ 20 đến 50:

  • Tập hợp $T$ chứa vượt quá ví dụ về "blue" nhãn (tối đa 35% cho ngưỡng 35).
  • Tập hợp $F$ chứa mức thâm hụt bổ sung của "blue" ví dụ về nhãn (chỉ 8% cho ngưỡng 35).

  Cả "tỷ lệ nhãn màu xanh" và "entropy" biểu đồ cho biết rằng nhãn có thể được phân tách tương đối tốt trong phạm vi ngưỡng này.

• Quan sát này được xác nhận trong "thông tin lợi nhuận" cốt truyện. Chúng tôi thấy rằng mức tăng thông tin tối đa thu được với t~=28 cho giá trị mức tăng thông tin là ~0,074. Do đó, điều kiện mà bộ chia trả về sẽ là $x \geq 28$.

• Lượng thông tin thu được luôn là số dương hoặc rỗng. Giá trị này hội tụ về 0 khi giá trị ngưỡng hội tụ về giá trị tối đa / tối thiểu. Trong những trường hợp đó, $F$ hoặc $T$ sẽ trống trong khi lớp còn lại chứa toàn bộ tập dữ liệu và hiển thị một entropy bằng giá trị trong $D$. Lượng thông tin thu được cũng có thể bằng 0 khi $H(T)$ = $H(F)$ = $H(D)$. Ở ngưỡng 60, tỷ lệ "blue&quot là $0 và $0 tương ứng với $$

Các giá trị ứng viên cho $t$ trong tập hợp các số thực ($\mathbb{R}$) là vô hạn. Tuy nhiên, với một số ví dụ hữu hạn, chỉ tồn tại một số hạn chế hữu hạn là $D$ thành $T$ và $F$. Do đó, chỉ có một số lượng giá trị hữu hạn là $t$ mới có ý nghĩa với việc kiểm thử.

Cách tiếp cận cổ điển là sắp xếp các giá trị x_i theo thứ tự tăng dần x_s(i) sao cho:

$$ x_{s(i)} \leq x_{s(i+1)} $$

Sau đó, hãy thử $t$ cho mọi giá trị nằm giữa các giá trị được sắp xếp liên tiếp là $x_i$. Ví dụ: giả sử bạn có 1.000 giá trị dấu phẩy động của một tính năng cụ thể. Sau khi sắp xếp, giả sử hai giá trị đầu tiên là 8,5 và 8,7. Trong trường hợp này, giá trị ngưỡng đầu tiên để kiểm thử sẽ là 8,6.

Chính thức, chúng tôi xem xét các giá trị đề xuất sau cho t:

$$ X = \left\{ \frac {x_{s(i)} + x_{s(i + 1)}} {2} \lvert x_{s(i)} \ne x_{s(i+1)} \right\} $$

Độ phức tạp của thời gian của thuật toán này là $\mathcal{O} ( n \log n) $ với $n$ số ví dụ trong nút (do cách sắp xếp các giá trị tính năng). Khi áp dụng một cây quyết định, thuật toán của bộ chia sẽ được áp dụng cho từng nút và từng tính năng. Lưu ý rằng mỗi nút nhận khoảng ~1/2 ví dụ thành phần mẹ. Do đó, theo nguyên tắc chính, sự phức tạp về thời gian của việc đào tạo cây quyết định bằng bộ chia này là:

$$ \mathcal{O} ( m n \log^2 n ) $$

nơi:

• $m$ là số lượng đối tượng.
• $n$ là số ví dụ về đào tạo.

Trong thuật toán này, giá trị của các tính năng không quan trọng; chỉ có ý nghĩa về thứ tự. Vì lý do này, thuật toán này hoạt động độc lập với quy mô hoặc sự phân phối các giá trị tính năng. Đây là lý do tại sao chúng ta không cần phải chuẩn hoá hoặc điều chỉnh tỷ lệ các tính năng dạng số khi huấn luyện cây quyết định.