Splitter esatto per la classificazione binaria con caratteristiche numeriche

In questa unità esaminerai l'algoritmo di suddivisione più semplice e comune, che crea condizioni del tipo $\mathrm{feature}_i \geq t$ nella seguente impostazione:

• Attività di classificazione binaria
• Senza valori mancanti negli esempi
• Senza indice precalcolato sugli esempi

Supponiamo un insieme di $n$ esempi con un attributo numerico e un'etichetta binaria "arancione" e "blu". Formalmente, descriviamo il set di dati $D$ come:

$$D = \{(x_i,y_i)\}_{i\in[1,n]}$$

dove:

• $x_i$ è il valore di una caratteristica numerica in $\mathbb{R}$ (l'insieme dei numeri reali).
• $y_i$ è un valore dell'etichetta di classificazione binaria in {orange, blue}.

Il nostro obiettivo è trovare un valore di soglia $t$ (soglia) tale che la suddivisione degli esempi $D$ nei gruppi $T(rue)$ e $F(alse)$ in base alla condizione $x_i \geq t$ migliori la separazione delle etichette; ad esempio, più esempi "arancioni" in $T$ e più esempi "blu" in $F$.

L'entropia di Shannon è una misura del disordine. Per un'etichetta binaria:

• L'entropia di Shannon è massima quando le etichette negli esempi sono bilanciate (50% blu e 50% arancione).
• L'entropia di Shannon è minima (valore zero) quando le etichette negli esempi sono pure (100% blu o 100% arancione).

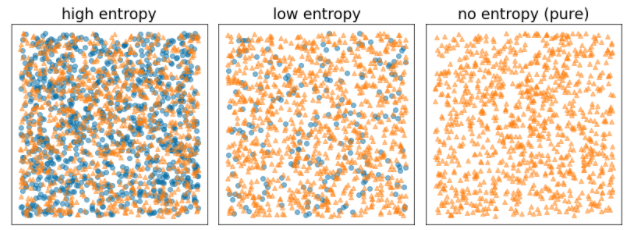
Figura 8. Tre diversi livelli di entropia.

 

Formalmente, vogliamo trovare una condizione che diminuisca la somma ponderata dell'entropia delle distribuzioni delle etichette in $T$ e $F$. Il punteggio corrispondente è il guadagno di informazione, ovvero la differenza tra l'entropia di $D$ e l'entropia di {$T$,$F$}. Questa differenza viene chiamata guadagno di informazione.

La figura seguente mostra una suddivisione errata, in cui l'entropia rimane elevata e il guadagno informativo è basso:

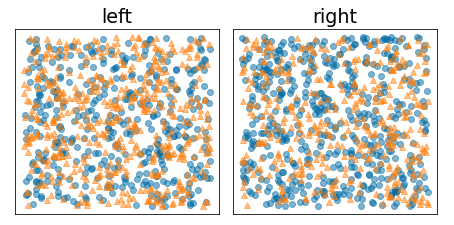
Figura 9. Una suddivisione errata non riduce l'entropia dell'etichetta.

 

Al contrario, la figura seguente mostra una suddivisione migliore in cui l'entropia diventa bassa (e l'aumento dell'informazione è elevato):

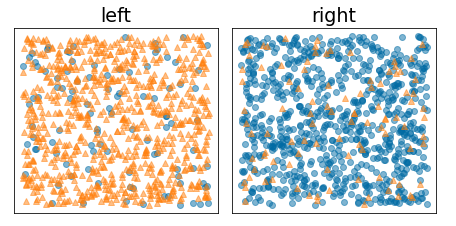
Figura 10. Una suddivisione efficace riduce l'entropia dell'etichetta.

 

In forma ufficiale:

\[\begin{eqnarray} T & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \ge t \} \\[12pt] F & = & \{ (x_i,y_i) | (x_i,y_i) \in D \ \textrm{with} \ x_i \lt t \} \\[12pt] R(X) & = & \frac{\lvert \{ x | x \in X \ \textrm{and} \ x = \mathrm{pos} \} \rvert}{\lvert X \rvert} \\[12pt] H(X) & = & - p \log p - (1 - p) \log (1-p) \ \textrm{with} \ p = R(X)\\[12pt] IG(D,T,F) & = & H(D) - \frac {\lvert T\rvert} {\lvert D \rvert } H(T) - \frac {\lvert F \rvert} {\lvert D \rvert } H(F) \end{eqnarray}\]

dove:

• $IG(D,T,F)$ è l'incremento dell'informazione derivante dalla suddivisione di $D$ in $T$ e $F$.
• $H(X)$ è l'entropia dell'insieme di esempi $X$.
• $|X|$ è il numero di elementi nell'insieme $X$.
• $t$ è il valore soglia.
• $pos$ è il valore dell'etichetta positivo, ad esempio "blu" nell'esempio riportato sopra. La scelta di un'etichetta diversa come "etichetta positiva" non cambia il valore dell'entropia o dell'incremento dell'informazione.
• $R(X)$ è il rapporto tra i valori delle etichette positive negli esempi $X$.
• $D$ è il set di dati (come definito in precedenza in questa unità).

Nell'esempio seguente, consideriamo un set di dati di classificazione binaria con una singola caratteristica numerica $x$. La figura seguente mostra per diversi valori della soglia $t$ (asse x):

1. L'istogramma della funzionalità $x$.
2. Il rapporto tra gli esempi "blu" negli insiemi $D$, $T$ e $F$ in base al valore di soglia.
3. L'entropia in $D$, $T$ e $F$.
4. Il guadagno di informazione, ovvero il delta di entropia tra $D$ e {$T$,$F$} pesato in base al numero di esempi.

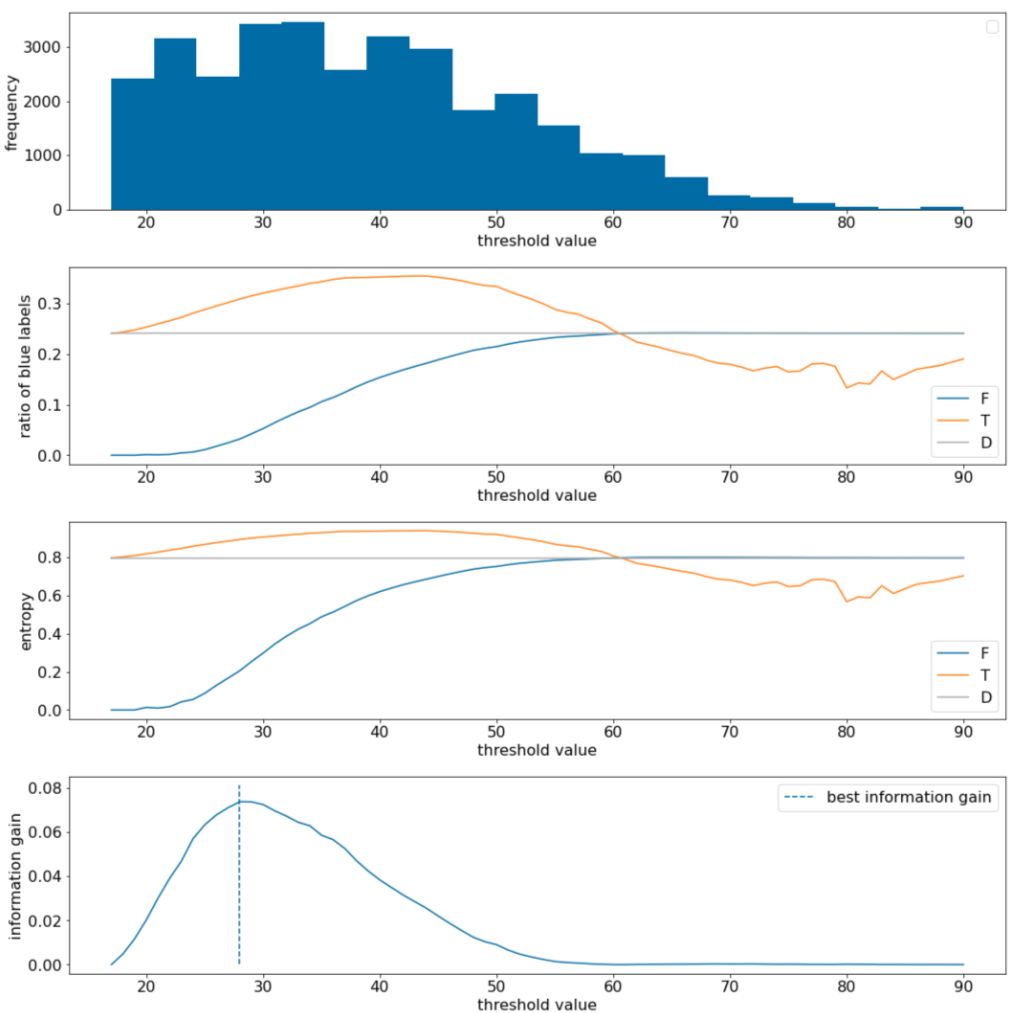
Figura 11. Quattro grafici di soglie.

 

Questi grafici mostrano quanto segue:

• Il grafico "Frequenza" mostra che le osservazioni sono relativamente ben distribuite con concentrazioni tra 18 e 60. Un'ampia distribuzione dei valori indica che esistono molte potenziali suddivisioni, il che è positivo per l'addestramento del modello.

• Il rapporto tra le etichette "blu" nel set di dati è di circa il 25%. Il grafico "Rapporto di etichetta blu" indica che per valori di soglia compresi tra 20 e 50:

  • L'insieme $T$ contiene un eccesso di esempi di etichette "blu" (fino al 35% per la soglia 35).
  • L'insieme $F$ contiene un deficit complementare di esempi di etichette "blu" (solo l'8% per la soglia 35).

  Sia il grafico "Rapporto di etichette blu" sia il grafico "Entropia" indicano che le etichette possono essere relativamente ben separate in questo intervallo di soglie.

• Questa osservazione è confermata nel grafico "guadagno di informazioni". Vediamo che l'incremento massimo dell'informazione viene ottenuto con t~=28 per un valore di incremento dell'informazione di circa 0,074. Pertanto, la condizione restituita dallo splitter sarà $x \geq 28$.

• Il guadagno informativo è sempre positivo o nullo. Convergono a zero man mano che il valore di soglia convergono verso il valore massimo / minimo. In questi casi, $F$ o $T$ diventano vuoti, mentre l'altro contiene l'intero set di dati e mostra un'entropia uguale a quella di $D$. Il guadagno informativo può essere zero anche quando $H(T)$ = $H(F)$ = $H(D)$. Al valore di soglia 60, i rapporti delle etichette "blu" sia per $T$ che per $F$ sono uguali a quelli di $D$ e il guadagno informativo è zero.

I valori candidati per $t$ nell'insieme dei numeri reali ($\mathbb{R}$) sono infiniti. Tuttavia, dato un numero finito di esempi, esiste solo un numero finito di suddivisioni di D in T ed F. Pertanto, solo un numero finito di valori di t è significativo per il test.

Un approccio classico è ordinare i valori x_i in ordine crescente x_s(i) in modo che:

$$ x_{s(i)} \leq x_{s(i+1)} $$

Poi, testa $t$ per ogni valore a metà tra i valori ordinati consecutivi di $x_i$. Ad esempio, supponiamo di avere 1000 valori in virgola mobile di una determinata funzionalità. Dopo l'ordinamento, supponiamo che i primi due valori siano 8,5 e 8,7. In questo caso, il primo valore di soglia da testare sarà 8,6.

Formalmente, consideriamo i seguenti valori candidati per t:

$$ X = \left\{ \frac {x_{s(i)} + x_{s(i + 1)}} {2} \lvert x_{s(i)} \ne x_{s(i+1)} \right\} $$

La complessità temporale di questo algoritmo è $\mathcal{O} ( n \log n) $ con $n$ il numero di esempi nel nodo (a causa dell'ordinamento dei valori delle caratteristiche). Quando viene applicato a un albero decisionale, l'algoritmo di suddivisione viene applicato a ogni nodo e a ogni funzionalità. Tieni presente che ogni nodo riceve circa la metà degli esempi del nodo principale. Pertanto, in base al teorema magistrale, la complessità temporale dell'addestramento di un albero decisionale con questo suddivisore è:

$$ \mathcal{O} ( m n \log^2 n ) $$

dove:

• $m$ è il numero di elementi.
• $n$ è il numero di esempi di addestramento.

In questo algoritmo, il valore delle funzionalità non è importante; è importante solo l'ordine. Per questo motivo, questo algoritmo funziona indipendentemente dalla scala o dalla distribuzione dei valori delle funzionalità. Questo è il motivo per cui non è necessario normalizzare o estendere le caratteristiche numeriche durante l'addestramento di uno schema decisionale.