דף זה תורגם על ידי Cloud Translation API.

סוגים של תנאים

היחידה הזו מתמקדת בסוגים שונים של תנאים שמשמשים ליצירת עצי החלטות.

תנאים לאורך ציר לעומת תנאים בזווית

תנאי במישור ציר כרוך רק בתכונה אחת. תנאי עקיף כרוך בכמה מאפיינים. לדוגמה, זהו תנאי שתואמת לציר:

num_legs ≥ 2

לעומת זאת, זהו תנאי עקיף:

num_legs ≥ num_fingers

לעיתים קרובות, עצי החלטות מאומנים רק עם תנאים שמותאמים לציר. עם זאת, חלוקות אופקיות יעילות יותר כי הן יכולות לבטא דפוסים מורכבים יותר. לפעמים, חלוקות אופקיות מניבות תוצאות טובות יותר, אבל על חשבון עלויות גבוהות יותר של אימון והסקה.

קוד YDF

ב-YDF, עצי החלטות מאומנים עם תנאי שתואמים לציר כברירת מחדל. אפשר להפעיל עצים של החלטות משוטים באמצעות הפרמטר split_axis="SPARSE_OBLIQUE".

התנאי שמוכן לציר הוא "num_legs >= 3". התנאי העקיף הוא

"num_legs + weight * 5 >= 12".

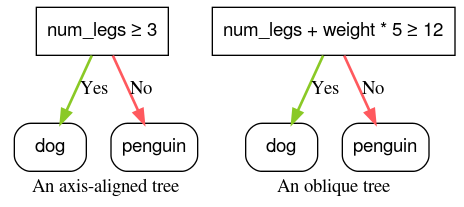
איור 4. דוגמאות לתנאי לאורך ציר ולתנאי משופע.

הצגת שני התנאים הקודמים בתרשים מובילה להפרדה הבאה במרחב המאפיינים:

תרשים של weight לעומת num_legs. התנאי 'התאמה לציר' מתעלם מהמשקל, ולכן הוא רק קו אנכי. התנאי משופע מראה קו עם שיפוע שלילי.

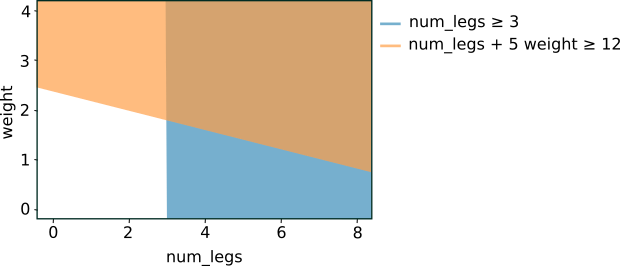
איור 5. הפרדה במרחב התכונות לתנאים שמוצגים באיור 4.

תנאים בינאריים לעומת תנאים לא בינאריים

תנאים עם שני תוצאות אפשריות (לדוגמה, true או false) נקראים תנאים בינאריים. עצי החלטות שמכילים רק תנאים בינאריים נקראים עצי החלטות בינאריים.

לתנאים לא בינאריים יש יותר משתי תוצאות אפשריות. לכן, לתנאים לא בינאריים יש יותר יכולת להבחין בין קבוצות מאשר לתנאים בינאריים. החלטות שמכילות תנאי לא בינארי אחד או יותר נקראות עצים של החלטות לא בינאריות.

השוואה בין עצי החלטה בינאריים לעצים לא בינאריים. עץ ההחלטות הבינארי מכיל שני תנאים בינאריים, ועץ ההחלטות הלא בינארי מכיל תנאי אחד לא בינארי.

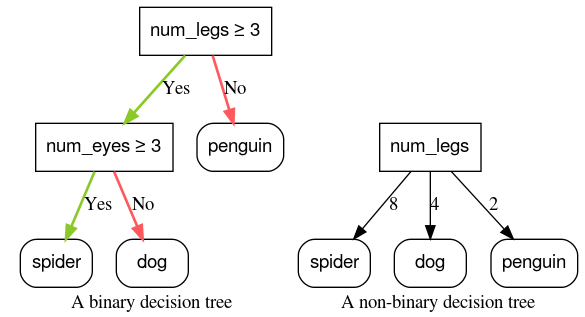
איור 6: עצי החלטה בינאריים לעומת עצי החלטה לא בינאריים.

תנאים עם עוצמה גדולה מדי נוטים יותר להתאמה יתר. לכן, בדרך כלל משתמשים ביערות החלטות עם עצי החלטות בינאריים, ולכן הקורס הזה יתמקד בהם.

הסוג הנפוץ ביותר של תנאי הוא תנאי סף שמתבטא באופן הבא:

feature ≥ threshold

לדוגמה:

num_legs ≥ 2

יש סוגים אחרים של תנאים. אלה סוגי תנאים בינאריים נפוצים נוספים:

טבלה 2. סוגים נפוצים של תנאים בינאריים.

שם	Condition	דוגמה
תנאי סף	$\mathrm{feature}_i \geq \mathrm{threshold}$	‎ $\mathrm{num\_legs} \geq 2$ ‎
תנאי שוויון	‎ $\mathrm{feature}_i = \mathrm{value}$ ‎	‎ $\mathrm{species} = ``cat"$ ‎
תנאי בקבוצה	‎ $\mathrm{feature}_i \in \mathrm{collection}$ ‎	‎ $\mathrm{species} \in \{``cat", ``dog", ``bird"\}$ ‎
תנאי משופע	‎ $\sum_{i} \mathrm{weight}_i \mathrm{feature}_i \geq \mathrm{threshold}$ ‎	‎ $5 \ \mathrm{num\_legs} + 2 \ \mathrm{num\_eyes} \geq 10$ ‎
התכונה חסרה	$\mathrm{feature}_i \mathrm{is} \mathrm{Missing}$	‎ $\mathrm{num\_legs} \mathrm{is} \mathrm{Missing}$ ‎

סקירה כללית

בדיקת ההבנה