Esta unidade se concentra em diferentes tipos de condições usadas para criar árvores de decisão.
Condições alinhadas ao eixo x oblíquas
Uma condição alinhada ao eixo envolve apenas um único elemento. Uma condição oblíqua envolve vários recursos. Por exemplo, a seguir está uma condição alinhada ao eixo:
num_legs ≥ 2
Já esta é uma condição oblíqua:
num_legs ≥ num_fingers
Muitas vezes, as árvores de decisão são treinadas apenas com condições alinhadas ao eixo. No entanto, as divisões oblíquas são mais poderosas porque podem expressar padrões mais complexos. As divisões oblíquas às vezes produzem resultados melhores à custa de custos de treinamento e inferência mais altos.
split_axis="SPARSE_OBLIQUE".
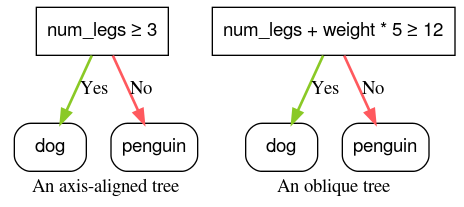
Figura 4. Exemplos de uma condição alinhada ao eixo e uma oblíqua.
O gráfico das duas condições anteriores gera a seguinte separação de espaço de recursos:
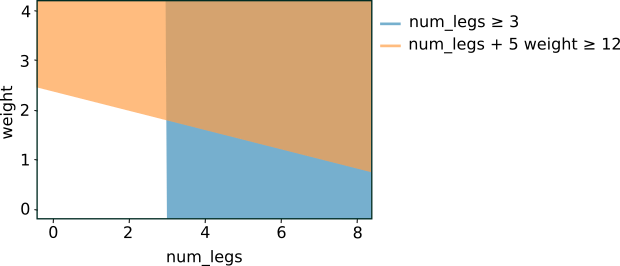
Figura 5. Separação do espaço de recursos para as condições na Figura 4.
Condições binárias e não binárias
Condições com dois resultados possíveis (por exemplo, verdadeiro ou falso) são chamadas de condições binárias. As árvores de decisão que contêm apenas condições binárias são chamadas de árvores de decisão binárias.
As condições não binárias têm mais de dois resultados possíveis. Portanto, as condições não binárias têm mais poder de discriminação do que as condições binárias. As decisões que contêm uma ou mais condições não binárias são chamadas de árvores de decisão não binárias.
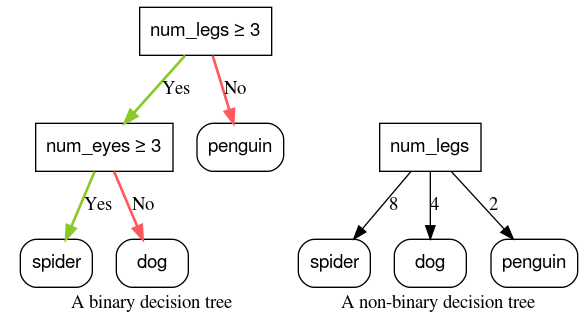
Figura 6: árvores de decisão binária e não binária.
Condições com muita potência também têm mais chances de apresentar overfitting. Por esse motivo, as florestas de decisão geralmente usam árvores de decisão binárias. Portanto, este curso vai se concentrar nelas.
O tipo mais comum de condição é a condição de limite expressa como:
feature ≥ threshold
Exemplo:
num_legs ≥ 2
Existem outros tipos de condições. Confira a seguir outros tipos de condições binárias usados com frequência:
Tabela 2. Tipos comuns de condições binárias.
| Nome | Condição | Exemplo |
| condição de limite | $\mathrm{feature}_i \geq \mathrm{threshold}$ | $\mathrm{num\_legs} \geq 2$ |
| condição de igualdade | $\mathrm{feature}_i = \mathrm{value}$ | $\mathrm{species} = ``cat"$ |
| condição no conjunto | $\mathrm{feature}_i \in \mathrm{collection}$ | $\mathrm{species} \in \{``cat", ``dog", ``bird"\}$ |
| condição oblíqua | $\sum_{i} \mathrm{weight}_i \mathrm{feature}_i \geq \mathrm{threshold}$ | $5 \ \mathrm{num\_legs} + 2 \ \mathrm{num\_eyes} \geq 10$ |
| recurso ausente | $\mathrm{feature}_i \mathrm{is} \mathrm{Missing}$ | $\mathrm{num\_legs} \mathrm{is} \mathrm{Missing}$ |