В этом модуле основное внимание уделяется различным типам условий , используемых для построения деревьев решений.
Условия выравнивания по оси и наклона
Условие выравнивания по оси включает только один объект. Наклонное условие включает в себя несколько функций. Например, следующее условие выравнивания по оси:
num_legs ≥ 2
В то время как следующее является косвенным условием:
num_legs ≥ num_fingers
Часто деревья решений обучаются только с использованием условий, выровненных по осям. Однако косые разделения более эффективны, поскольку могут выражать более сложные закономерности. Косое разбиение иногда дает лучшие результаты за счет более высоких затрат на обучение и логические выводы.
split_axis="SPARSE_OBLIQUE" . 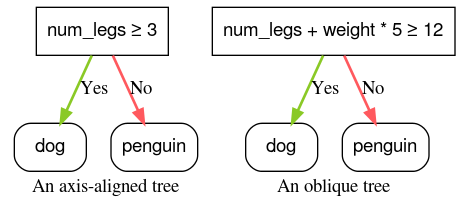
Рисунок 4. Примеры условий выравнивания по оси и наклона.
Построение графика двух предыдущих условий дает следующее разделение пространства признаков:
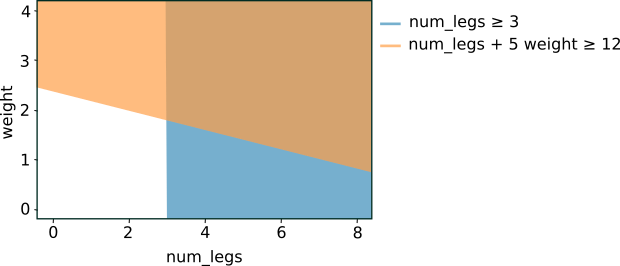
Рисунок 5. Разделение пространства признаков для условий, показанных на рисунке 4.
Двоичные и небинарные условия
Условия с двумя возможными исходами (например, истина или ложь) называются бинарными условиями . Деревья решений, содержащие только бинарные условия, называются бинарными деревьями решений .
Небинарные условия имеют более двух возможных результатов. Следовательно, небинарные условия обладают большей дискриминационной силой, чем бинарные. Решения, содержащие одно или несколько небинарных условий, называются небинарными деревьями решений .
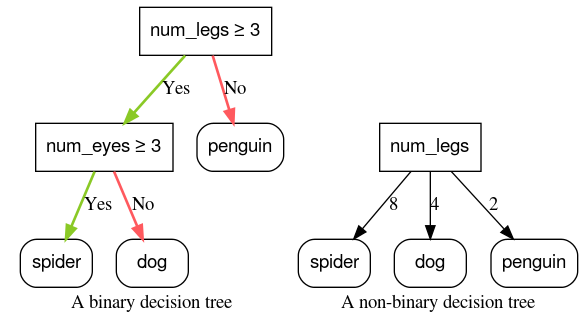
Рисунок 6: Двоичные и недвоичные деревья решений.
Условия со слишком большой мощностью также с большей вероятностью переобучаются. По этой причине в лесах решений обычно используются бинарные деревья решений, поэтому в этом курсе основное внимание будет уделено им.
Наиболее распространенным типом состояния является пороговое состояние, выражаемое как:
feature ≥ threshold
Например:
num_legs ≥ 2
Существуют и другие типы условий. Ниже приведены другие часто используемые типы бинарных условий:
Таблица 2. Распространенные типы бинарных условий.
| Имя | Состояние | Пример |
| пороговое состояние | $\mathrm{feature}_i \geq \mathrm{threshold}$ | $\mathrm{num\_legs} \geq 2$ |
| условие равенства | $\mathrm{feature}_i = \mathrm{value}$ | $\mathrm{species} = ``кошка"$ |
| в установленном состоянии | $\mathrm{feature}_i \in \mathrm{collection}$ | $\mathrm{species} \in \{``кошка", ``собака", ``птица"\}$ |
| косое состояние | $\sum_{i} \mathrm{weight}_i \mathrm{feature}_i \geq \mathrm{threshold}$ | $5 \ \mathrm{num\_legs} + 2 \ \mathrm{num\_eyes} \geq 10$ |
| функция отсутствует | $\mathrm{feature}_i \mathrm{is} \mathrm{Missing}$ | $\mathrm{num\_legs} \mathrm{is} \mathrm{Missing}$ |
