本單元將著重於用於建立決策樹的不同類型條件。
對齊軸與斜向條件
軸對齊 條件只涉及單一地圖項目。斜向條件涉及多個特徵。例如,以下是與軸對齊的條件:
num_legs ≥ 2
以下則為斜線條件:
num_legs ≥ num_fingers
決策樹通常只會以與軸對齊的條件進行訓練。不過,斜線分割符更強大,因為它可以表示更複雜的模式。斜向分割有時會產生更好的結果,但訓練和推論成本會提高。
YDF 代碼
在 YDF 中,決策樹預設會使用與軸對齊的條件進行訓練。您可以使用 split_axis="SPARSE_OBLIQUE" 參數啟用決策斜向樹狀圖。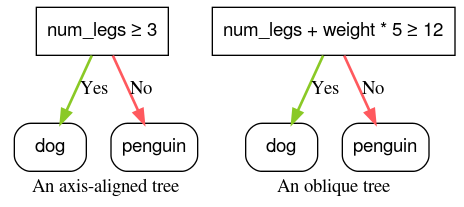
圖 4. 軸對齊條件和斜向條件的範例。
將上述兩個條件繪製成圖表,可產生下列特徵空間分隔:
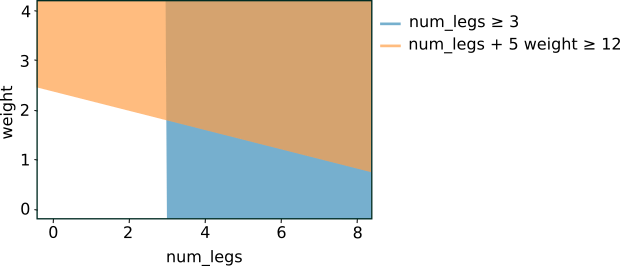
圖 5. 圖 4 中條件的特徵空間分離。
二元條件與非二元條件
有兩種可能結果的條件 (例如 true 或 false) 稱為二元條件。只包含二元條件的決策樹稱為二元決策樹。
非二元條件有超過兩種可能的結果。因此,非二元條件比二元條件具有更強的判別能力。包含一或多個非二元條件的決策稱為非二元決策樹。
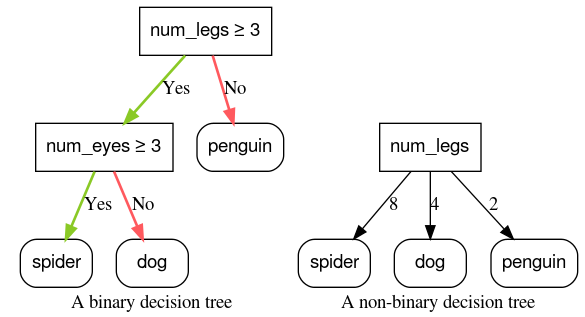
圖 6:二元與非二元決策樹狀圖。
過度強大的條件也較有可能過度擬合。因此,決策樹通常會使用二元決策樹,因此本課程會著重於這類樹狀圖。
最常見的條件類型是門檻條件,表示方式如下:
feature ≥ threshold
例如:
num_legs ≥ 2
還有其他類型的條件。以下是其他常用的二元條件類型:
表 2. 常見的二元條件類型。
| 名稱 | 狀況 | 示例 |
| 門檻條件 | $\mathrm{feature}_i \geq \mathrm{threshold}$ | $\mathrm{num\_legs} \geq 2$ |
| 相等條件 | $\mathrm{feature}_i = \mathrm{value}$ | $\mathrm{species} = ``cat"$ |
| 在集合內的條件 | $\mathrm{feature}_i \in \mathrm{collection}$ | $\mathrm{species} \in \{``cat", ``dog", ``bird"\}$ |
| 斜線條件 | $\sum_{i} \mathrm{weight}_i \mathrm{feature}_i \geq \mathrm{threshold}$ | $5 \ \mathrm{num\_legs} + 2 \ \mathrm{num\_eyes} \geq 10$ |
| 缺少功能 | $\mathrm{feature}_i \mathrm{is} \mathrm{Missing}$ | $\mathrm{num\_legs} \mathrm{is} \mathrm{Missing}$ |
