In diesem Modul geht es um verschiedene Arten von Bedingungen, die zum Erstellen von Entscheidungsbäumen verwendet werden.
Achsenorientierte und schräge Bedingungen
Eine Achsenausrichtungsbedingung bezieht sich nur auf ein einzelnes Element. Eine schräge Bedingung bezieht sich auf mehrere Features. Hier ist beispielsweise eine achsenunabhängige Bedingung zu sehen:
num_legs ≥ 2
Die folgende Bedingung ist indirekt:
num_legs ≥ num_fingers
Häufig werden Entscheidungsbäume nur mit achsorientierten Bedingungen trainiert. Schrägachsen sind jedoch leistungsfähiger, da sie komplexere Muster ausdrücken können. Schrägachsen-Splits führen manchmal zu besseren Ergebnissen, allerdings zu höheren Trainings- und Inferenzkosten.
split_axis="SPARSE_OBLIQUE" aktivieren.
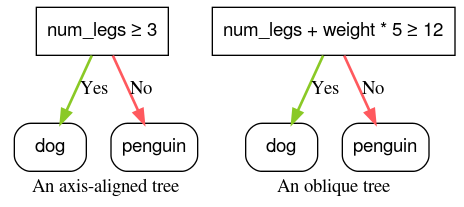
Abbildung 4. Beispiele für eine achsenunabhängige Bedingung und eine schräge Bedingung.
Wenn Sie die beiden vorherigen Bedingungen grafisch darstellen, ergibt sich die folgende Trennung des Merkmalsraums:
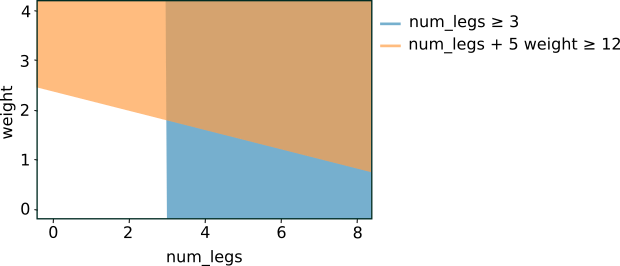
Abbildung 5. Trennung des Feature-Bereichs für die Bedingungen in Abbildung 4.
Binäre und nicht binäre Bedingungen
Bedingungen mit zwei möglichen Ergebnissen (z. B. wahr oder falsch) werden als binäre Bedingungen bezeichnet. Entscheidungsbäume, die nur binäre Bedingungen enthalten, werden als binäre Entscheidungsbäume bezeichnet.
Nicht binäre Bedingungen haben mehr als zwei mögliche Ergebnisse. Daher haben nicht binäre Bedingungen eine größere Unterscheidungskraft als binäre Bedingungen. Entscheidungen mit einer oder mehreren nicht binären Bedingungen werden als nicht binäre Entscheidungsbäume bezeichnet.
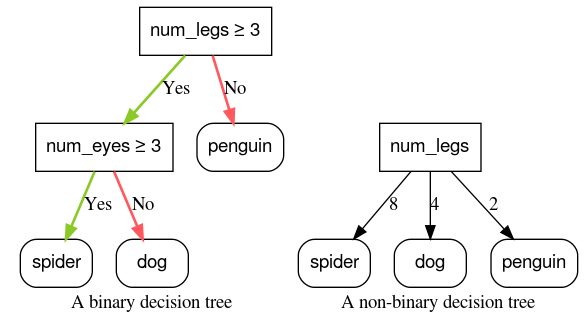
Abbildung 6: Binäre und nicht binäre Entscheidungsbäume.
Bei Bedingungen mit zu viel Gewichtung ist die Wahrscheinlichkeit einer Überanpassung ebenfalls höher. Aus diesem Grund werden in Entscheidungswäldern in der Regel binäre Entscheidungsbäume verwendet. In diesem Kurs liegt der Schwerpunkt daher auf diesen.
Die gängigste Art von Bedingung ist die Grenzwertbedingung, die so ausgedrückt wird:
feature ≥ threshold
Beispiel:
num_legs ≥ 2
Es gibt noch weitere Arten von Bedingungen. Im Folgenden finden Sie weitere häufig verwendete Arten von binären Bedingungen:
Tabelle 2. Gängige Arten binärer Bedingungen.
| Name | Bedingung | Beispiel |
| Schwellenwertbedingung | $\mathrm{feature}_i \geq \mathrm{threshold}$ | $\mathrm{num\_legs} \geq 2$ |
| Gleichheitsbedingung | $\mathrm{feature}_i = \mathrm{value}$ | $\mathrm{species} = ``cat"$ |
| Bedingung im Set | $\mathrm{feature}_i \in \mathrm{collection}$ | $\mathrm{species} \in \{``cat", ``dog", ``bird"\}$ |
| Schrägachsenprojektion | $\sum_{i} \mathrm{weight}_i \mathrm{feature}_i \geq \mathrm{threshold}$ | $5 \ \mathrm{num\_legs} + 2 \ \mathrm{num\_eyes} \geq 10$ |
| Funktion fehlt | $\mathrm{feature}_i \mathrm{is} \mathrm{Missing}$ | $\mathrm{num\_legs} \mathrm{is} \mathrm{Missing}$ |