इस यूनिट में, अलग-अलग तरह की शर्तों पर फ़ोकस किया जाता है. इन शर्तों का इस्तेमाल, डिसीज़न ट्री बनाने के लिए किया जाता है.
अक्ष के साथ अलाइन होने वाली बनाम ऑब्लिक स्थितियां
ऐक्सिस के साथ अलाइन की गई शर्त में सिर्फ़ एक फ़ीचर शामिल होता है. तिरछी शर्त में कई सुविधाएं शामिल होती हैं. उदाहरण के लिए, यहां दी गई शर्त, अक्ष के साथ अलाइन की गई है:
num_legs ≥ 2
जबकि यह एक अस्पष्ट शर्त है:
num_legs ≥ num_fingers
आम तौर पर, डिसिज़न ट्री को सिर्फ़ ऐक्सिस के अलाइन होने की शर्तों के साथ ट्रेन किया जाता है. हालांकि, ऑब्लिक स्प्लिट ज़्यादा असरदार होते हैं, क्योंकि इनसे ज़्यादा जटिल पैटर्न दिखाए जा सकते हैं. कभी-कभी, ऑब्लिक स्प्लिट से बेहतर नतीजे मिलते हैं. हालांकि, इसके लिए ट्रेनिंग और अनुमान लगाने की लागत ज़्यादा होती है.
split_axis="SPARSE_OBLIQUE" पैरामीटर की मदद से, डिसीज़न ऑब्लिक ट्री चालू किए जा सकते हैं.
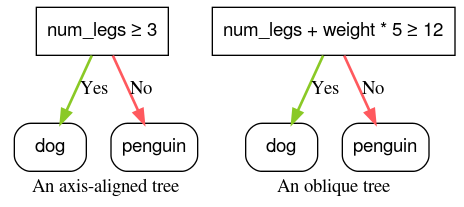
चौथी इमेज. अक्ष के साथ अलाइन की गई शर्त और तिरछी शर्त के उदाहरण.
ऊपर दी गई दो शर्तों को ग्राफ़ में दिखाने पर, सुविधाओं के बीच का फ़र्क़ इस तरह दिखता है:
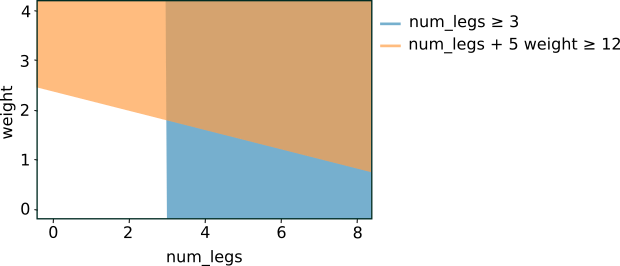
पांचवां चित्र. चौथी इमेज में दी गई शर्तों के लिए, फ़ीचर स्पेस को अलग करना.
बाइनरी बनाम नॉन-बाइनरी शर्तें
दो संभावित नतीजों (उदाहरण के लिए, सही या गलत) वाली शर्तों को बाइनरी शर्तें कहा जाता है. सिर्फ़ बाइनरी शर्तों वाले डिसीज़न ट्री को बाइनरी डिसीज़न ट्री कहा जाता है.
नॉन-बाइनरी शर्तों के दो से ज़्यादा संभावित नतीजे हो सकते हैं. इसलिए, बिनेरी कंडीशन के मुकाबले नॉन-बाइनरी कंडीशन में, भेदभाव करने की क्षमता ज़्यादा होती है. एक या उससे ज़्यादा नॉन-बाइनरी शर्तों वाले फ़ैसलों को नॉन-बाइनरी डिसीज़न ट्री कहा जाता है.
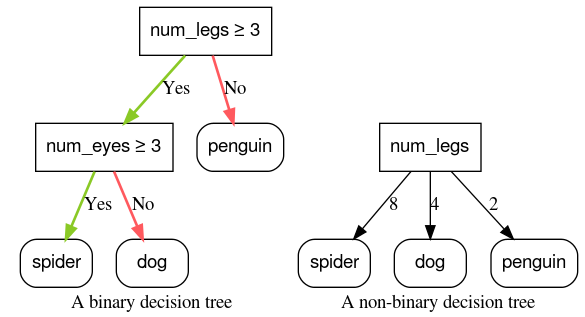
छठी इमेज: बाइनरी बनाम नॉन-बाइनरी डिसीज़न ट्री.
बहुत ज़्यादा वैल्यू वाली शर्तों के लिए भी, मॉडल के ओवरफ़िट होने की संभावना ज़्यादा होती है. इस वजह से, डिसीज़न फ़ॉरेस्ट आम तौर पर बाइनरी डिसीज़न ट्री का इस्तेमाल करते हैं. इसलिए, इस कोर्स में इन पर फ़ोकस किया जाएगा.
सबसे आम टाइप की शर्त, थ्रेशोल्ड शर्त होती है. इसे इस तरह दिखाया जाता है:
feature ≥ threshold
उदाहरण के लिए:
num_legs ≥ 2
अन्य तरह की शर्तें भी मौजूद हैं. आम तौर पर इस्तेमाल होने वाली अन्य बाइनरी शर्तें यहां दी गई हैं:
दूसरी टेबल. बाइनरी शर्तों के सामान्य टाइप.
| नाम | शर्त | उदाहरण |
| थ्रेशोल्ड की शर्त | $\mathrm{feature}_i \geq \mathrm{threshold}$ | $\mathrm{num\_legs} \geq 2$ |
| बराबरी की शर्त | $\mathrm{feature}_i = \mathrm{value}$ | $\mathrm{species} = ``cat"$ |
| इन-सेट स्थिति | $\mathrm{feature}_i \in \mathrm{collection}$ | $\mathrm{species} \in \{``cat", ``dog", ``bird"\}$ |
| ऑब्लिक कंडीशन | $\sum_{i} \mathrm{weight}_i \mathrm{feature}_i \geq \mathrm{threshold}$ | $5 \ \mathrm{num\_legs} + 2 \ \mathrm{num\_eyes} \geq 10$ |
| सुविधा मौजूद नहीं है | $\mathrm{feature}_i \mathrm{is} \mathrm{Missing}$ | $\mathrm{num\_legs} \mathrm{is} \mathrm{Missing}$ |