এই ইউনিট সিদ্ধান্ত গাছ তৈরি করতে ব্যবহৃত বিভিন্ন ধরনের অবস্থার উপর ফোকাস করে।
অক্ষ-সারিবদ্ধ বনাম তির্যক অবস্থা
একটি অক্ষ-সারিবদ্ধ অবস্থায় শুধুমাত্র একটি বৈশিষ্ট্য জড়িত। একটি তির্যক অবস্থা একাধিক বৈশিষ্ট্য জড়িত। উদাহরণস্বরূপ, নিম্নলিখিতটি একটি অক্ষ-সারিবদ্ধ শর্ত:
num_legs ≥ 2
যদিও নিম্নলিখিত একটি তির্যক অবস্থা:
num_legs ≥ num_fingers
প্রায়শই, সিদ্ধান্ত গাছ শুধুমাত্র অক্ষ-সারিবদ্ধ অবস্থার সাথে প্রশিক্ষিত হয়। যাইহোক, তির্যক বিভাজন আরও শক্তিশালী কারণ তারা আরও জটিল নিদর্শন প্রকাশ করতে পারে। তির্যক বিভাজন কখনও কখনও উচ্চতর প্রশিক্ষণ এবং অনুমান খরচের খরচে আরও ভাল ফলাফল দেয়।
split_axis="SPARSE_OBLIQUE" প্যারামিটার দিয়ে সিদ্ধান্ত তির্যক গাছ সক্ষম করতে পারেন। 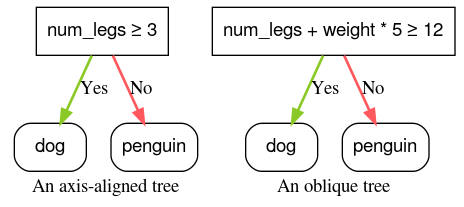
চিত্র 4. একটি অক্ষ-সারিবদ্ধ অবস্থা এবং একটি তির্যক অবস্থার উদাহরণ।
পূর্ববর্তী দুটি অবস্থার গ্রাফ করা নিম্নলিখিত বৈশিষ্ট্য স্থান বিচ্ছেদ প্রদান করে:

চিত্র 5. চিত্র 4-এ শর্তগুলির জন্য স্থান বিভাজনের বৈশিষ্ট্য।
বাইনারি বনাম নন-বাইনারী শর্ত
দুটি সম্ভাব্য ফলাফল সহ শর্তগুলি (উদাহরণস্বরূপ, সত্য বা মিথ্যা) বাইনারি অবস্থা বলা হয়। শুধুমাত্র বাইনারি শর্তযুক্ত ডিসিশন ট্রিকে বাইনারি ডিসিশন ট্রি বলা হয়।
নন-বাইনারী অবস্থার দুটির বেশি সম্ভাব্য ফলাফল রয়েছে। অতএব, বাইনারি অবস্থার তুলনায় নন-বাইনারী অবস্থার বেশি বৈষম্যমূলক শক্তি রয়েছে। এক বা একাধিক নন-বাইনারী শর্ত সম্বলিত সিদ্ধান্তকে নন-বাইনারী সিদ্ধান্ত গাছ বলা হয়।
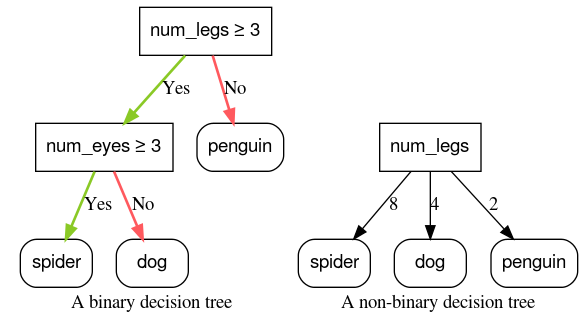
চিত্র 6: বাইনারি বনাম অ-বাইনারি সিদ্ধান্ত গাছ।
অত্যধিক শক্তি সহ শর্তগুলিও ওভারফিট হওয়ার সম্ভাবনা বেশি। এই কারণে, সিদ্ধান্ত বন সাধারণত বাইনারি সিদ্ধান্ত গাছ ব্যবহার করে, তাই এই কোর্সটি তাদের উপর ফোকাস করবে।
অবস্থার সবচেয়ে সাধারণ ধরনের হল থ্রেশহোল্ড শর্ত হিসাবে প্রকাশ করা হয়:
feature ≥ threshold
যেমন:
num_legs ≥ 2
অন্যান্য ধরনের শর্ত বিদ্যমান। নিম্নলিখিত বাইনারি অবস্থার অন্যান্য সাধারণভাবে ব্যবহৃত ধরনের:
সারণি 2. বাইনারি অবস্থার সাধারণ প্রকার।
| নাম | অবস্থা | উদাহরণ |
| প্রান্তিক অবস্থা | $\mathrm{feature}_i \geq \mathrm{threshold}$ | $\mathrm{num\_legs} \geq 2$ |
| সমতা শর্ত | $\mathrm{feature__i = \mathrm{value}$ | $\mathrm{species} = ``বিড়াল"$ |
| ইন-সেট অবস্থা | $\mathrm{feature__i \in \mathrm{collection}$ | $\mathrm{species} \in \{``cat", ``dog", ``bird"\}$ |
| তির্যক অবস্থা | $\sum_{i} \mathrm{weight}_i \mathrm{feature}_i \geq \mathrm{threshold}$ | $5 \ \mathrm{num\_legs} + 2 \ \mathrm{num\_eyes} \geq 10$ |
| বৈশিষ্ট্য অনুপস্থিত | $\mathrm{feature__i \mathrm{is} \mathrm{মিসিং}$ | $\mathrm{num\_legs} \mathrm{is} \mathrm{মিসিং}$ |
