หน่วยนี้มุ่งเน้นที่เงื่อนไขประเภทต่างๆ ที่ใช้ในการสร้างแผนภูมิการตัดสินใจ
เงื่อนไขที่สอดคล้องกับแกนกับเงื่อนไขที่เอียง
เงื่อนไข ที่สอดคล้องกับแกนเกี่ยวข้องกับองค์ประกอบเพียงรายการเดียว เงื่อนไขแบบเอียงเกี่ยวข้องกับองค์ประกอบหลายอย่าง ตัวอย่างเช่น เงื่อนไขต่อไปนี้เป็นเงื่อนไขที่สอดคล้องกับแกน
num_legs ≥ 2
ส่วนเงื่อนไขต่อไปนี้เป็นเงื่อนไขแบบอ้อม
num_legs ≥ num_fingers
บ่อยครั้งที่ต้นไม้การตัดสินใจได้รับการฝึกด้วยเงื่อนไขที่สอดคล้องกับแกนเท่านั้น อย่างไรก็ตาม การแยกแนวเฉียงมีประสิทธิภาพมากกว่าเนื่องจากสามารถแสดงรูปแบบที่ซับซ้อนมากขึ้น บางครั้งการแยกแนวเฉียงจะให้ผลลัพธ์ที่ดีกว่า แต่ก็ต้องแลกมาด้วยค่าใช้จ่ายในการฝึกและการอนุมานที่สูงขึ้น
split_axis="SPARSE_OBLIQUE"
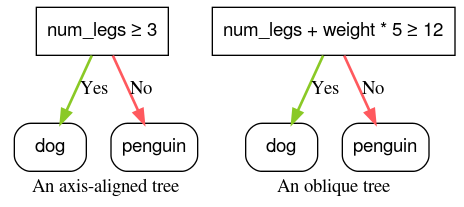
รูปที่ 4 ตัวอย่างเงื่อนไขที่สอดคล้องกับแกน และเงื่อนไขที่เอียง
การเขียนกราฟของเงื่อนไข 2 ข้อก่อนหน้าจะให้การแยกพื้นที่ลักษณะต่อไปนี้
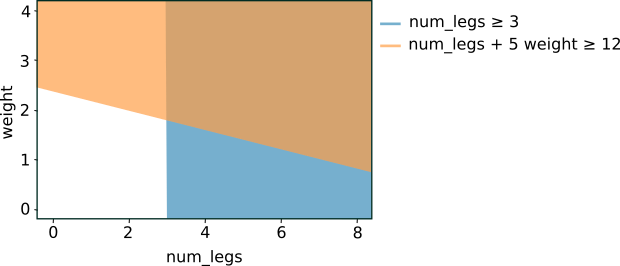
รูปที่ 5 การแยกพื้นที่ลักษณะของเงื่อนไขในรูปที่ 4
เงื่อนไขแบบไบนารีกับแบบไม่ไบนารี
เงื่อนไขที่มีผลลัพธ์ที่เป็นไปได้ 2 รายการ (เช่น จริงหรือเท็จ) เรียกว่าเงื่อนไขไบนารี แผนผังการตัดสินใจที่มีเฉพาะเงื่อนไขแบบไบนารีเรียกว่าแผนผังการตัดสินใจแบบไบนารี
เงื่อนไขที่ไม่ใช่แบบ 2 ค่าจะมีผลลัพธ์ที่เป็นไปได้มากกว่า 2 รายการ ดังนั้น เงื่อนไขที่ไม่ใช่แบบไบนารีจึงมีความสามารถในการแยกแยะมากกว่าเงื่อนไขแบบไบนารี การตัดสินใจที่มีเงื่อนไขที่ไม่ใช่แบบ 2 ค่าอย่างน้อย 1 รายการเรียกว่าต้นไม้การตัดสินใจที่ไม่ใช่แบบ 2 ค่า
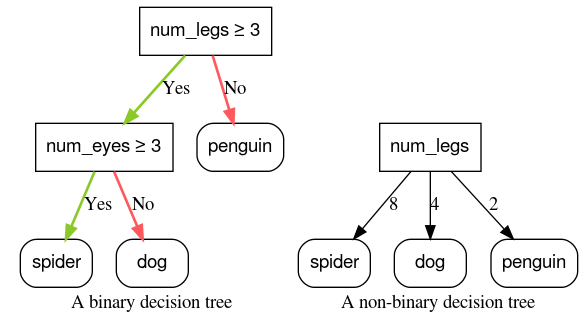
รูปที่ 6: แผนภูมิการตัดสินใจแบบไบนารีกับแบบไม่ไบนารี
เงื่อนไขที่มีกำลังมากเกินไปก็มีแนวโน้มที่จะปรับให้พอดีมากเกินไปด้วย ด้วยเหตุนี้ ป่าการตัดสินใจจึงมักใช้แผนผังการตัดสินใจแบบไบนารี ดังนั้นหลักสูตรนี้จะมุ่งเน้นที่แผนผังดังกล่าว
เงื่อนไขประเภทที่พบบ่อยที่สุดคือเงื่อนไขเกณฑ์ที่แสดงเป็น
feature ≥ threshold
เช่น
num_legs ≥ 2
เงื่อนไขประเภทอื่นๆ ก็มี เงื่อนไขไบนารีประเภทอื่นๆ ที่มักใช้มีดังนี้
ตาราง 2 เงื่อนไขไบนารีประเภทต่างๆ ที่พบบ่อย
| ชื่อ | Condition | ตัวอย่าง |
| เงื่อนไขเกณฑ์ | $\mathrm{feature}_i \geq \mathrm{threshold}$ | $\mathrm{num\_legs} \geq 2$ |
| เงื่อนไขความเท่าเทียม | $\mathrm{feature}_i = \mathrm{value}$ | $\mathrm{species} = ``cat"$ |
| เงื่อนไขในชุด | $\mathrm{feature}_i \in \mathrm{collection}$ | $\mathrm{species} \in \{``cat", ``dog", ``bird"\}$ |
| เงื่อนไขเอียง | $\sum_{i} \mathrm{weight}_i \mathrm{feature}_i \geq \mathrm{threshold}$ | $5 \ \mathrm{num\_legs} + 2 \ \mathrm{num\_eyes} \geq 10$ |
| ไม่มีฟีเจอร์ | $\mathrm{feature}_i \mathrm{is} \mathrm{Missing}$ | $\mathrm{num\_legs} \mathrm{is} \mathrm{Missing}$ |