이 단원에서는 의사결정 트리를 만드는 데 사용되는 다양한 유형의 조건에 중점을 둡니다.
축 정렬 조건과 경사 조건
축에 정렬된 조건은 단일 지형지물만 포함합니다. 경사 조건에는 여러 지형지물이 포함됩니다. 예를 들어 다음은 축에 정렬된 조건입니다.
num_legs ≥ 2
다음은 경사 조건입니다.
num_legs ≥ num_fingers
결정 트리는 축에 정렬된 조건으로만 학습되는 경우가 많습니다. 그러나 더 복잡한 패턴을 표현할 수 있으므로 경사 분할이 더 강력합니다. 경사 분할은 학습 및 추론 비용이 더 많이 들지만 더 나은 결과를 얻을 수 있습니다.
split_axis="SPARSE_OBLIQUE" 매개변수를 사용하여 결정 경사형 트리를 사용 설정할 수 있습니다.
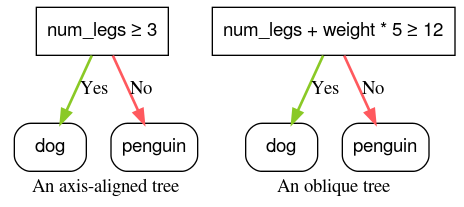
그림 4. 축에 정렬된 조건과 경사 조건의 예시입니다.
위의 두 조건을 그래프로 표시하면 다음과 같은 특징 공간 분리가 나타납니다.
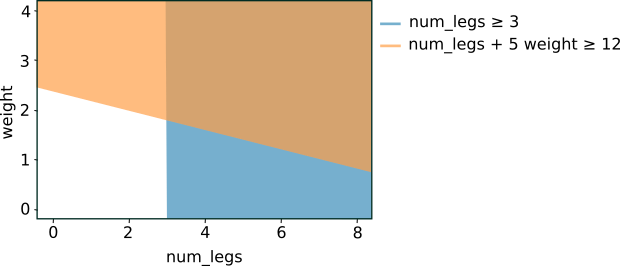
그림 5. 그림 4의 조건에 대한 특성 공간 분리.
바이너리 조건과 비바이너리 조건
가능한 두 가지 결과 (예: true 또는 false)가 있는 조건을 이진 조건이라고 합니다. 바이너리 조건만 포함된 결정 트리를 바이너리 결정 트리라고 합니다.
비바이너리 조건에는 두 가지 이상의 결과가 있을 수 있습니다. 따라서 바이너리 외 조건은 바이너리 조건보다 더 높은 판별력을 갖습니다. 하나 이상의 비바이너리 조건이 포함된 결정을 비바이너리 결정 트리라고 합니다.
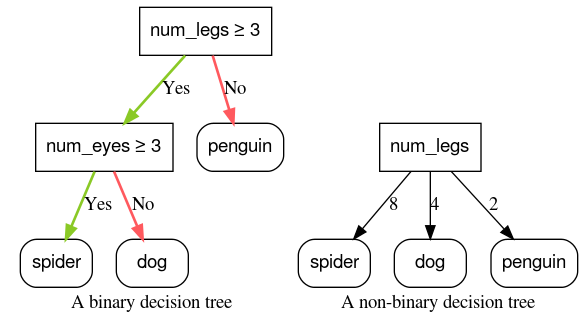
그림 6: 바이너리 결정 트리와 비바이너리 결정 트리 비교
또한 검증력이 너무 강한 조건은 과적합될 가능성이 높습니다. 이 때문에 결정 숲은 일반적으로 이진 결정 트리를 사용하므로 이 과정에서는 이진 결정 트리에 중점을 둡니다.
가장 일반적인 조건 유형은 다음과 같이 표현되는 기준점 조건입니다.
feature ≥ threshold
예를 들면 다음과 같습니다.
num_legs ≥ 2
다른 유형의 조건도 있습니다. 다음은 흔히 사용되는 다른 유형의 이진 조건입니다.
표 2. 일반적인 유형의 바이너리 조건입니다.
| 이름 | 조건 | 예 |
| 임곗값 조건 | $\mathrm{feature}_i \geq \mathrm{threshold}$ | $\mathrm{num\_legs} \geq 2$ |
| 등식 조건 | $\mathrm{feature}_i = \mathrm{value}$ | $\mathrm{species} = ``cat"$ |
| in-set 조건 | $\mathrm{feature}_i \in \mathrm{collection}$ | $\mathrm{species} \in \{``cat", ``dog", ``bird"\}$ |
| 경사 조건 | $\sum_{i} \mathrm{weight}_i \mathrm{feature}_i \geq \mathrm{threshold}$ | $5 \ \mathrm{num\_legs} + 2 \ \mathrm{num\_eyes} \geq 10$ |
| 기능이 누락됨 | $\mathrm{feature}_i \mathrm{is} \mathrm{Missing}$ | $\mathrm{num\_legs} \mathrm{is} \mathrm{Missing}$ |