Arbres de décision: tester vos connaissances

Cette page vous invite à répondre à une série d'exercices à choix multiples sur le contenu abordé dans le module "Arbres de décision".

Question 1

L'inférence d'un arbre de décision s'exécute en acheminant un exemple...
de la feuille à la racine.
Toutes les inférences commencent à la racine (première condition).
d'une feuille à l'autre.
Toutes les inférences commencent par la racine, et non par une feuille.
de la racine à la feuille.
Bravo !

Question 2

Toutes les conditions ne concernent-elles qu'une seule fonctionnalité ?
Oui.
Les éléments obliques testent plusieurs éléments.
Non.
Bien que les conditions alignées sur l'axe ne concernent qu'un seul élément géographique, les conditions obliques en impliquent plusieurs.

Question 3

Prenons la carte de prédiction suivante sur deux caractéristiques x1 et x2:

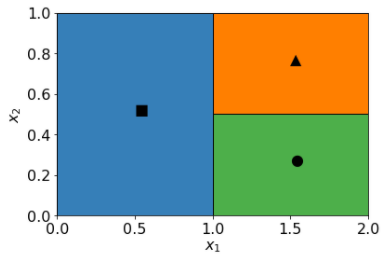
Carte avec deux axes: x1, qui s'étend de 0,0 à 2,0, et x2, qui s'étend de 0,0 à 1,0. La carte est organisée en trois zones contiguës. La zone bleue définit un rectangle couvrant x1 de 0,0 à 1,0 et x2 de 0,0 à 1,0. La zone verte définit un rectangle couvrant x1 de 1,0 à 2,0 et x2 de 0 à 0,5. La zone orange définit un rectangle couvrant x1 de 1,0 à 2,0 et x2 de 0,5 à 1,0.

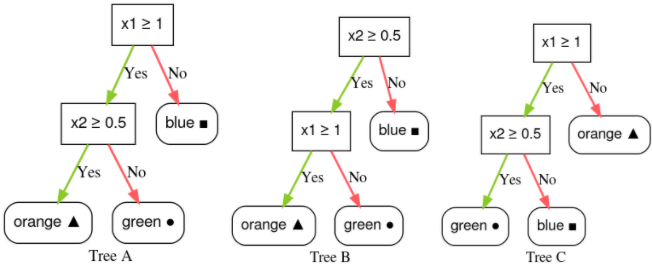
Parmi les arbres de décision suivants, lesquels correspondent à la carte de prédiction ? Trois arbres de décision, chacun contenant deux conditions. La racine de l'arbre de décision A est "x1 >= 1". Si ce n'est pas le cas, la feuille est "bleue". Sinon, la deuxième condition est "x2 >= 0,5". Si la deuxième condition est remplie, la feuille est "orange". Dans le cas contraire, elle est "verte". La racine de l'arbre de décision B est "x2 >= 0,5". Si ce n'est pas le cas, la feuille est "blue". Si oui, la deuxième condition est "x1 >= 1.0". Si la deuxième condition est remplie, la feuille est "orange". Dans le cas contraire, elle est "verte". La racine de l'arbre de décision C est "x1 >= 1". Si ce n'est pas le cas, la feuille est "orange". Sinon, la deuxième condition est "x2 >= 0,5". Si la deuxième condition est remplie, la feuille est "verte". Dans le cas contraire, elle est "bleue".
Arbre de décision A.
Oui.
Arbre de décision B.
Si la condition x2 ≥ 0, 5 est non, la feuille peut être bleue ou non.Il s'agit donc d'une mauvaise condition.
Arbre de décision C.
Si x1 n'est pas ≥ 1, 0, la feuille doit être "bleue" plutôt qu'"orange". Il s'agit donc de la mauvaise feuille.
Précédent
Conditions
Suivant
Arbres de décision en pleine croissance