すべての教師あり ML モデルと同様に、ディシジョン ツリーは、一連のトレーニング サンプルを最も適切に説明するようにトレーニングされます。ディシジョン ツリーの最適なトレーニングは NP 困難な問題です。したがって、トレーニングは通常、ヒューリスティクスを使用して行われます。ヒューリスティクスは、最適ではないが最適に近い決定木を生成できる、作成が簡単な学習アルゴリズムです。
ディシジョン ツリーのトレーニングに使用されるほとんどのアルゴリズムは、貪欲な分割統治戦略で動作します。このアルゴリズムは、単一のノード(ルート)を作成することから始まり、再帰的に貪欲に決定木を成長させます。
各ノードで、考えられるすべての条件が評価され、スコアが付けられます。アルゴリズムは「最適な」条件(スコアが最も高い条件)を選択します。スコアはタスクと関連する指標であり、その指標を最大化するように条件が選択されることを理解しておいてください。
たとえば、Palmer Penguins データセット(このコースの後半のコード例で使用)では、ほとんどのアデリーペンギンとチンストラップペンギンのくちばしの長さが 16 mm を超えるのに対し、ほとんどのジェンツーペンギンのくちばしの長さは短くなります。したがって、条件 bill_length_mm ≥ 16 はジェンツーペンギンの予測をほぼ完璧に行うことができますが、アデリーペンギンとチンストラップペンギンを区別することはできません。アルゴリズムはおそらくこの条件を選択します。

図 7. 木を育てる最初のステップです。
その後、アルゴリズムは両方の子ノードで再帰的に独立して繰り返します。条件を満たすノードが見つからない場合、ノードはリーフになります。リーフ予測は、サンプルで最も代表的なラベル値として決定されます。
アルゴリズムは次のとおりです。
def train_decision_tree(training_examples):
root = create_root() # Create a decision tree with a single empty root.
grow_tree(root, training_examples) # Grow the root node.
return root
def grow_tree(node, examples):
condition = find_best_condition(examples) # Find the best condition.
if condition is None:
# No satisfying conditions were found, therefore the grow of the branch stops.
set_leaf_prediction(node, examples)
return
# Create two childrens for the node.
positive_child, negative_child = split_node(node, condition)
# List the training examples used by each children.
negative_examples = [example for example in examples if not condition(example)]
positive_examples = [example for example in examples if condition(example)]
# Continue the growth of the children.
grow_tree(negative_child, negative_examples)
grow_tree(positive_child, positive_examples)
特定のディシジョン ツリーをトレーニングする手順について詳しく説明します。
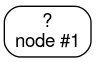
ステップ 1: ルートを作成します。
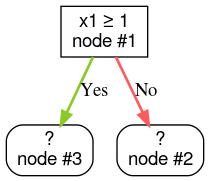
ステップ 2: ノード 1 を拡張します。「x1 ≥ 1」という条件が見つかりました。2 つの子ノードが作成されます。
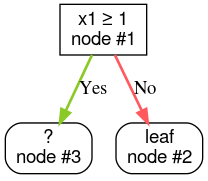
ステップ 3: ノード 2 を拡張します。条件を満たす条件は見つかりませんでした。ノードからリーフを作成します。
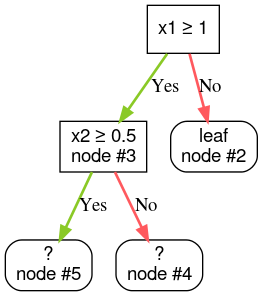
ステップ 4: ノード 3 を拡張します。「x2 ≥ 0.5」という条件が見つかりました。2 つの子ノードが作成されます。
ディシジョン ツリーを成長させる方法は他にもあります。分割統治戦略を使用する代わりに、ノードをグローバルに最適化することも一般的です。
growing_strategy="BEST_FIRST_GLOBAL" パラメータを使用してグローバルな成長を有効にすることもできます。詳しくは、
ドキュメントをご覧ください。入力特徴の数とタイプによっては、特定のノードで可能な条件の数は非常に大きくなり、通常は無限になります。たとえば、しきい値条件 $\mathrm{feature}_i \geq t$ が与えられた場合、$t \in \mathbb{R}$ のすべての可能なしきい値の組み合わせは無限です。
最適な条件を見つけるルーティンは、分割ツールと呼ばれます。分割ツールは、考えられる多くの条件をテストする必要があるため、ディシジョン ツリーをトレーニングする際のボトルネックになります。
分割ツールによって最大化されるスコアはタスクによって異なります。次に例を示します。
分割アルゴリズムには多くの種類があり、それぞれ次のようなサポートが異なります。
- 特徴のタイプ(数値、カテゴリ、テキストなど)
- タスク(バイナリ分類、多クラス分類、回帰など)
- 条件のタイプ(しきい値条件、セット内条件、斜め条件など)
- 正規化条件(しきい値条件の正確な分割または近似分割など)
さらに、メモリ使用量、CPU 使用量、計算分散などに関して異なるトレードオフがある同等の分割ツールがあります。