Tüm gözetimli makine öğrenimi modelleri gibi karar ağaçları da bir dizi eğitim örneğini en iyi şekilde açıklamak için eğitilir. Karar ağacının optimum eğitimi NP-zor bir problemdir. Bu nedenle, eğitim genellikle heuristikler kullanılarak yapılır. Heuristikler, optimum olmayan ancak optimuma yakın bir karar ağacı veren, oluşturulması kolay bir öğrenme algoritmasıdır.
Karar ağaçlarını eğitmek için kullanılan çoğu algoritma, açgözlü bir bölme ve fethetme stratejisiyle çalışır. Algoritma, tek bir düğüm (kök) oluşturarak başlar ve karar ağacını yinelemeli ve açgözlü bir şekilde büyütür.
Her düğümde, olası tüm koşullar değerlendirilir ve puanlanır. Algoritma, "en iyi" koşulu, yani en yüksek puana sahip koşulu seçer. Puanın, görevle ilişkili bir metrik olduğunu ve koşulların bu metriği en üst düzeye çıkaracak şekilde seçildiğini bilmenizde fayda var.
Örneğin, Palmer penguenleri veri kümesinde (bu dersin ilerleyen bölümlerindeki kod örnekleri için kullanılır), Adelie ve Gentoo penguenlerinin çoğunun gagası 16 mm'den uzundur. Bu nedenle, bill_length_mm ≥ 16 koşulu Gentoo penguenleri için neredeyse mükemmel tahminler yapar ancak Adelie ve Chinstrap penguenleri arasında ayrım yapamaz. Algoritma büyük olasılıkla bu koşulu seçer.

Şekil 7. Ağaç yetiştirmenin ilk adımı.
Ardından algoritma, her iki alt düğümde de yinelemeli ve bağımsız olarak tekrarlanır. Uygun koşul bulunmadığında düğüm bir yaprak olur. Yaprak tahmini, örneklerdeki en temsili etiket değeri olarak belirlenir.
Algoritma şu şekildedir:
def train_decision_tree(training_examples):
root = create_root() # Create a decision tree with a single empty root.
grow_tree(root, training_examples) # Grow the root node.
return root
def grow_tree(node, examples):
condition = find_best_condition(examples) # Find the best condition.
if condition is None:
# No satisfying conditions were found, therefore the grow of the branch stops.
set_leaf_prediction(node, examples)
return
# Create two childrens for the node.
positive_child, negative_child = split_node(node, condition)
# List the training examples used by each children.
negative_examples = [example for example in examples if not condition(example)]
positive_examples = [example for example in examples if condition(example)]
# Continue the growth of the children.
grow_tree(negative_child, negative_examples)
grow_tree(positive_child, positive_examples)
Belirli bir karar ağacını eğitme adımlarını daha ayrıntılı bir şekilde inceleyelim.
1. Adım: Kök oluşturun:
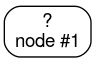
2. adım: 1. düğümü büyütün. "x1 ≥ 1" koşulu bulundu. İki alt düğüm oluşturulur:
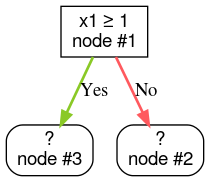
3. adım: 2. düğümü büyütün. Koşulları karşılayan bir sonuç bulunamadı. Dolayısıyla düğümü bir yaprak haline getirin:
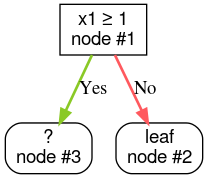
4. Adım: 3. düğümü büyütün. "x2 ≥ 0,5" koşulu bulundu. İki alt düğüm oluşturulur.
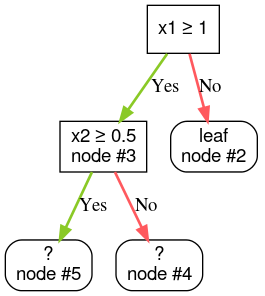
Karar ağaçları oluşturmanın başka yöntemleri de vardır. Bölme ve fethetme stratejisi kullanmak yerine düğümleri küresel olarak optimize etmek popüler bir alternatiftir.
growing_strategy="BEST_FIRST_GLOBAL" parametresini kullanarak global büyümeyi etkinleştirebilirsiniz.
Daha fazla ayrıntı için
dokümanları inceleyin.
Giriş özelliklerinin sayısına ve türüne bağlı olarak, belirli bir düğüm için olası koşulların sayısı çok büyük olabilir (genellikle sonsuzdur). Örneğin, $\mathrm{feature}_i \geq t$ eşik koşulu verildiğinde, $t \in \mathbb{R}$ için tüm olası eşik değerlerinin kombinasyonu sonsuzdur.
En iyi koşulu bulmakla sorumlu rutine ayırıcı denir. Birçok olası koşulu test etmesi gerektiğinden, bölücüler karar ağacı eğitirken darboğaz oluşturur.
Bölme aracı tarafından artırılan puan, göreve bağlıdır. Örneğin:
- Bilgi kazancı ve Gini (her ikisi de daha sonra ele alınacaktır) sınıflandırma için yaygın olarak kullanılır.
- Ortalama karesel hata, genellikle regresyon için kullanılır.
Her biri aşağıdakiler için farklı düzeyde destek sunan birçok bölme algoritması vardır:
- Özelliklerin türü (ör. sayısal, kategorik, metin)
- Görev (ör. ikili sınıflandırma, çok sınıflı sınıflandırma, regresyon)
- Koşul türü (ör. eşik koşulu, ayar içinde koşul, eğik koşul)
- Normalleştirme ölçütleri (ör. eşik koşulları için tam veya yaklaşık bölücüler)
Ayrıca, bellek kullanımı, CPU kullanımı, hesaplama dağıtımı vb. ile ilgili farklı dengeler içeren eşdeğer ayırıcı varyantları da vardır.