Podobnie jak wszystkie modele nadzorowanych systemów uczących się, drzewa decyzyjne są trenowane w taki sposób, aby jak najlepiej wyjaśniać zestaw przykładów treningowych. Optymalne wytrenowanie schematu decyzyjnego to problem trudny w rozwiązaniu w czasie wielomianowym. Dlatego trening jest zwykle przeprowadzany za pomocą heurystyki – łatwego w utworzeniu algorytmu uczenia się, który daje drzewo decyzyjne nieoptymalne, ale zbliżone do optymalnego.
Większość algorytmów używanych do trenowania drzew decyzyjnych działa zgodnie ze strategią żarłocznego dziel i podbijaj. Algorytm zaczyna od utworzenia pojedynczego węzła (węzła głównego) i rekursywnie oraz żarłocznie rozbudowuje drzewo decyzyjne.
W każdym węźle wszystkie możliwe warunki są oceniane i przypisywane. Algorytm wybiera „najlepszy” stan, czyli stan o najwyższym wyniku. Na razie wystarczy wiedzieć, że wynik to dane, które są skorelowane z zadaniem, a warunki są wybierane w celu maksymalizacji tych danych.
Na przykład w zbiorze danych Palmer Penguins (używanym w przypadku przykładów kodu w dalszej części tego kursu) większość pingwinów Adelijskiego i Tundrowego ma dziób dłuższy niż 16 mm, a pingwiny białolica mają krótsze dzioby. Dlatego warunek bill_length_mm ≥ 16 zapewnia niemal idealne prognozy dotyczące pingwinów śnieżnych, ale nie pozwala odróżnić pingwinów Adeli i pingwinów białobrewych. Algorytm prawdopodobnie wybierze ten warunek.

Rysunek 7. Pierwszy krok w hodowaniu drzewa.
Następnie algorytm powtarza się rekurencyjnie i niezależnie na obu podrzędnych węzłach. Jeśli nie zostanie znaleziony żaden warunek, węzeł stanie się liściem. Prognoza na poziomie liścia jest określana jako najbardziej reprezentatywna wartość etykiety w przypadku przykładów.
Algorytm działa w ten sposób:
def train_decision_tree(training_examples):
root = create_root() # Create a decision tree with a single empty root.
grow_tree(root, training_examples) # Grow the root node.
return root
def grow_tree(node, examples):
condition = find_best_condition(examples) # Find the best condition.
if condition is None:
# No satisfying conditions were found, therefore the grow of the branch stops.
set_leaf_prediction(node, examples)
return
# Create two childrens for the node.
positive_child, negative_child = split_node(node, condition)
# List the training examples used by each children.
negative_examples = [example for example in examples if not condition(example)]
positive_examples = [example for example in examples if condition(example)]
# Continue the growth of the children.
grow_tree(negative_child, negative_examples)
grow_tree(positive_child, positive_examples)
Przyjrzyjmy się dokładniej etapom trenowania konkretnego schematu decyzyjnego.
Krok 1. Utwórz element rdzeniowy:
Krok 2. Rozwiń węzeł 1. Wykryto warunek „x1 ≥ 1”. Tworzone są 2 węzły podrzędne:
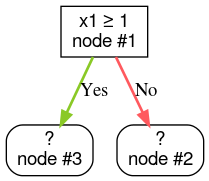
Krok 3. Rozwiń węzeł 2. Nie znaleziono warunków spełniających kryteria. Zmień węzeł na liść:
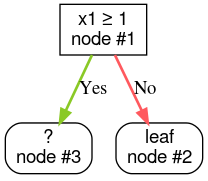
Krok 4. Rozwiń węzeł 3. Wykryto warunek „x2 ≥ 0,5”. Tworzone są 2 węzły podrzędne.
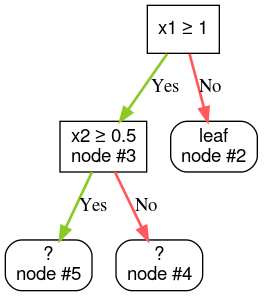
Istnieją też inne metody rozwijania drzewek decyzji. Popularną alternatywą jest globalna optymalizacja węzłów zamiast stosowania strategii „dziel i rządź”.
growing_strategy="BEST_FIRST_GLOBAL".
Aby dowiedzieć się więcej, zapoznaj się z
dokumentacją.
W zależności od liczby i typu danych wejściowych liczba możliwych warunków dla danego węzła może być ogromna, a na ogół nieskończona. Na przykład przy założeniu warunku progowego $\mathrm{feature}_i \geq t$ kombinacja wszystkich możliwych wartości progowych dla $t \in \mathbb{R}$ jest nieskończona.
Procedura odpowiedzialna za znajdowanie najlepszego warunku nosi nazwę splitter. Ponieważ musi testować wiele możliwych warunków, splittery są wąskim gardłem podczas trenowania drzewa decyzyjnego.
Wynik maksymalizowany przez splitter zależy od zadania. Przykład:
- Do klasyfikacji często stosuje się wzrost informacji i współczynnik Giniego (opisane poniżej).
- Błąd średniokwadratowy jest często używany do regresji.
Istnieje wiele algorytmów splitterów, z różnym poziomem obsługi:
- Typy cech, np. liczbowe, kategorialne, tekstowe
- zadanie, np. klasyfikacja binarna, klasyfikacja wieloklasowa, regresja;
- Typ warunku, np. warunek progowy, warunek w zestawie, warunek ukośny
- kryteria regularyzacji, np. rozdzielacze dokładne lub przybliżone w przypadku warunków progowych;
Dodatkowo istnieją równoważne warianty rozdzielaczy z różnymi kompromisami dotyczącymi wykorzystania pamięci, procesora, rozkładu obliczeń itp.