Wie alle überwachten ML-Modelle werden Entscheidungsbäume darauf trainiert, eine Reihe von Trainingsbeispielen. Das optimale Training eines Entscheidungsbaums ein NP-schweres Problem. Daher wird das Training in der Regel mithilfe von Heuristiken durchgeführt. einfach zu erstellenden Lernalgorithmus, der eine nicht optimale, aber Entscheidungsbaum.
Die meisten Algorithmen zum Trainieren von Entscheidungsbäumen arbeiten mit einer gierigen Kluft und erfolgreich zu sein. Der Algorithmus beginnt mit der Erstellung eines einzelnen Knotens (dem Stamm) und rekursiv und gierig wächst den Entscheidungsbaum.
An jedem Knoten werden alle möglichen Bedingungen ausgewertet und bewertet. Die der Algorithmus die „beste“ d. h. die Bedingung mit der höchsten Punkte. Im Moment reicht es, wenn Sie wissen, dass der Score ein Messwert ist, der mit dem Messwert und Bedingungen ausgewählt sind, um diesen Messwert zu maximieren.
Nehmen wir zum Beispiel im Palmer Pinguine (wird später in diesem Kurs für Codebeispiele verwendet), die meisten Adelie- und Zügel- Pinguine haben einen Schnabel von mehr als 16 mm, während die meisten Eselspinguine Pinguine haben kleinere Schnabeln. Dementsprechend ist die Bedingung bill_length_mm ≥ 16 liefert fast perfekte Vorhersagen für den Eselspinguine können aber nicht unterscheiden zwischen Adelies und Zügeln. Der Algorithmus wählt diese Bedingung wahrscheinlich aus.
<ph type="x-smartling-placeholder"></ph> Abbildung 7: Der erste Schritt beim Anbau eines Baums.
Der Algorithmus wiederholt sich dann rekursiv und unabhängig auf beiden untergeordneten Knoten. Wenn keine erfüllten Bedingungen gefunden werden, wird der Knoten zu einem Blatt. Das Blatt Vorhersage wird in den Beispielen als der repräsentativste Labelwert bestimmt.
Der Algorithmus sieht so aus:
def train_decision_tree(training_examples):
root = create_root() # Create a decision tree with a single empty root.
grow_tree(root, training_examples) # Grow the root node.
return root
def grow_tree(node, examples):
condition = find_best_condition(examples) # Find the best condition.
if condition is None:
# No satisfying conditions were found, therefore the grow of the branch stops.
set_leaf_prediction(node, examples)
return
# Create two childrens for the node.
positive_child, negative_child = split_node(node, condition)
# List the training examples used by each children.
negative_examples = [example for example in examples if not condition(example)]
positive_examples = [example for example in examples if condition(example)]
# Continue the growth of the children.
grow_tree(negative_child, negative_examples)
grow_tree(positive_child, positive_examples)
Sehen wir uns die Schritte zum Trainieren eines bestimmten Entscheidungsbaums um weitere Details zu erfahren.
Schritt 1:Stamm erstellen:
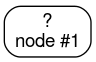
Schritt 2: Wachstum von Knoten 1. Die Bedingung „x1 ≥ 1“ wurde gefunden. Es werden zwei untergeordnete Knoten erstellt:
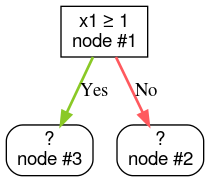
Schritt 3: Wachstum von Knoten 2. Es wurden keine erfüllenden Bedingungen gefunden. Stellen Sie sicher, dass der Knoten in ein Blatt zu verwandeln:
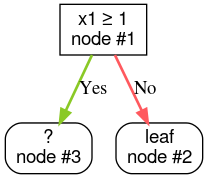
Schritt 4: Wachstum von Knoten 3. Die Bedingung „x2 ≥ 0.5“ wurde gefunden. Zwei Kinder Knoten erstellt werden.
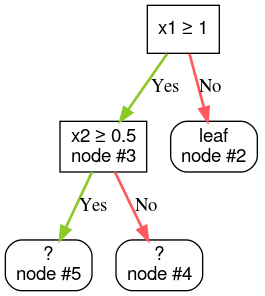
Es gibt noch andere Methoden, Entscheidungsbäume zu züchten. Eine beliebte Alternative ist Knoten global optimieren, anstatt eine Divide-and-Conquer-Strategie zu verwenden.
growing_strategy="BEST_FIRST_GLOBAL".
Weitere Informationen finden Sie unter .
finden Sie in der Dokumentation.
Je nach Anzahl und Art der Eingabemerkmale Die möglichen Bedingungen für einen Knoten können riesig und in der Regel unendlich sein. Beispiel: Bei einer Schwellenwertbedingung $\mathrm{feature}_i \geq t$, die Kombination aller möglich Schwellenwerte für $t \in \mathbb{R}$ ist unendlich.
Die Routine, die für die Suche nach der besten Bedingung verantwortlich ist, wird als Splitter. Da viele mögliche Bedingungen getestet werden müssen, sind die Engpässe beim Training eines Entscheidungsbaums.
Die vom Splitter maximierte Punktzahl hängt von der Aufgabe ab. Beispiel:
- Informationsgewinn und Gini (beide werden häufig für die Klassifizierung verwendet.
- Die mittlere quadratische Abweichung wird üblicherweise für Regressionen verwendet.
Es gibt viele Splitter-Algorithmen, die jeweils unterschiedliche Unterstützungen für Folgendes haben:
- Die Art der Funktionen Zum Beispiel „numerisch“, „kategorial“, „text“
- Die Aufgabe: Zum Beispiel binäre Klassifizierung, mehrere Klassen Klassifizierung, Regression
- Die Art der Bedingung, z. B. eine Schwellenwertbedingung, schräge Bedingung
- Die Regularisierungskriterien z. B. exakte oder ungefähre Aufteilungen für Schwellenwertbedingungen
Außerdem gibt es gleichwertige Splitter-Varianten mit unterschiedlichen Kompromissen. in Bezug auf Arbeitsspeichernutzung, CPU-Auslastung, Berechnungsverteilung usw.