Как и все модели машинного обучения с учителем, деревья решений обучаются так, чтобы лучше объяснять набор обучающих примеров. Оптимальное обучение дерева решений является NP-трудной задачей. Поэтому обучение обычно проводится с использованием эвристики — простого в создании алгоритма обучения, который дает неоптимальное, но близкое к оптимальному дерево решений.
Большинство алгоритмов, используемых для обучения деревьев решений, работают с жадной стратегией «разделяй и властвуй». Алгоритм начинается с создания одного узла (корня) и рекурсивно и жадно увеличивает дерево решений.
В каждом узле оцениваются и оцениваются все возможные условия. Алгоритм выбирает «лучшее» условие, то есть условие с наивысшим баллом. А пока просто знайте, что оценка — это метрика, которая коррелирует с задачей, и условия выбираются для максимизации этой метрики.
Например, в наборе данных Palmer Penguins (используемом для примеров кода далее в этом курсе) у большинства пингвинов Адели и Чинстрап длина клюва превышает 16 мм, тогда как у большинства пингвинов Генту клюв меньше. Следовательно, условие bill_length_mm ≥ 16 дает почти точные прогнозы для пингвинов Папуа, но не позволяет различить Адели и антарктических пингвинов. Алгоритм, вероятно, выберет это условие.
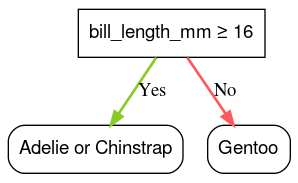
Рисунок 7. Первый шаг в выращивании дерева.
Затем алгоритм рекурсивно и независимо повторяется на обоих дочерних узлах. Если удовлетворяющих условий не обнаружено, узел становится листом. Предсказание листа определяется как наиболее репрезентативное значение метки в примерах.
Алгоритм следующий:
def train_decision_tree(training_examples):
root = create_root() # Create a decision tree with a single empty root.
grow_tree(root, training_examples) # Grow the root node.
return root
def grow_tree(node, examples):
condition = find_best_condition(examples) # Find the best condition.
if condition is None:
# No satisfying conditions were found, therefore the grow of the branch stops.
set_leaf_prediction(node, examples)
return
# Create two childrens for the node.
positive_child, negative_child = split_node(node, condition)
# List the training examples used by each children.
negative_examples = [example for example in examples if not condition(example)]
positive_examples = [example for example in examples if condition(example)]
# Continue the growth of the children.
grow_tree(negative_child, negative_examples)
grow_tree(positive_child, positive_examples)
Давайте рассмотрим этапы обучения конкретного дерева решений более подробно.
Шаг 1: Создайте корень:
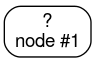
Шаг 2: Вырастите узел №1. Было обнаружено условие «x1 ≥ 1». Создаются два дочерних узла:
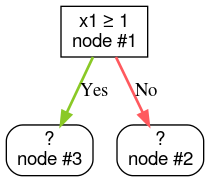
Шаг 3: Вырастите узел №2. Удовлетворительных условий не обнаружено. Итак, превратим узел в лист:
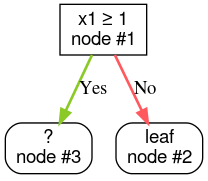
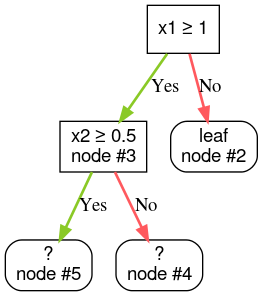
Шаг 4: Вырастите узел №3. Было обнаружено условие «x2 ≥ 0,5». Создаются два дочерних узла.
Существуют и другие методы выращивания деревьев решений. Популярной альтернативой является глобальная оптимизация узлов вместо использования стратегии «разделяй и властвуй».
growing_strategy="BEST_FIRST_GLOBAL" . Более подробную информацию смотрите в документации .В зависимости от количества и типа входных объектов количество возможных условий для данного узла может быть огромным, а иногда и бесконечным. Например, при заданном пороговом условии $\mathrm{feature}_i \geq t$ комбинация всех возможных пороговых значений для $t \in \mathbb{R}$ бесконечна.
Процедура, отвечающая за поиск наилучшего состояния, называется сплиттером . Поскольку необходимо проверить множество возможных условий, сплиттеры являются узким местом при обучении дерева решений.
Максимальный результат сплиттера зависит от задачи. Например:
- Прирост информации и коэффициент Джини (оба рассматриваются ниже) обычно используются для классификации.
- Среднеквадратическая ошибка обычно используется для регрессии.
Существует множество алгоритмов разделения, каждый из которых имеет разную поддержку:
- Тип функций; например, числовой, категориальный, текстовый
- Задача; например, бинарная классификация, многоклассовая классификация, регрессия
- Тип состояния; например, пороговое условие, установленное условие, наклонное условие
- Критерии регуляризации; например, точные или аппроксимированные разветвители для пороговых условий
Кроме того, существуют эквивалентные варианты разделителя с различными компромиссами в отношении использования памяти, использования ЦП, распределения вычислений и т. д.
