Al igual que todos los modelos de aprendizaje automático supervisado, los árboles de decisión se entrenan para explicar mejor un conjunto de ejemplos de entrenamiento. El entrenamiento óptimo de un árbol de decisión es un problema de NP duro. Por lo tanto, el entrenamiento suele realizarse con heurísticas, un algoritmo de aprendizaje fácil de crear que proporciona un árbol de decisión no óptimo, pero cercano al óptimo.
La mayoría de los algoritmos que se usan para entrenar árboles de decisión funcionan con una estrategia de división y conquista codiciosa. El algoritmo comienza por crear un solo nodo (la raíz) y crece el árbol de decisión de forma recursiva y codiciosa.
En cada nodo, se evalúan y puntúan todas las condiciones posibles. El algoritmo selecciona la "mejor" condición, es decir, la que tiene la puntuación más alta. Por ahora, ten en cuenta que la puntuación es una métrica que se correlaciona con la tarea, y las condiciones se seleccionan para maximizarla.
Por ejemplo, en el conjunto de datos de pingüinos de Palmer (que se usa para los ejemplos de código más adelante en este curso), la mayoría de los pingüinos Adelie y Chinstrap tienen una longitud de pico superior a 16 mm, mientras que la mayoría de los pingüinos Gentoo tienen picos más pequeños. Por lo tanto, la condición bill_length_mm ≥ 16 realiza predicciones casi perfectas para los pingüinos de barbijo, pero no puede diferenciar entre los pingüinos adelaida y los de barbijo. Es probable que el algoritmo elija esta condición.

Figura 7. El primer paso para cultivar un árbol.
Luego, el algoritmo se repite de forma recursiva e independiente en ambos nodos secundarios. Cuando no se encuentran condiciones que satisfagan, el nodo se convierte en hoja. La predicción de hoja se determina como el valor de etiqueta más representativo en los ejemplos.
El algoritmo es el siguiente:
def train_decision_tree(training_examples):
root = create_root() # Create a decision tree with a single empty root.
grow_tree(root, training_examples) # Grow the root node.
return root
def grow_tree(node, examples):
condition = find_best_condition(examples) # Find the best condition.
if condition is None:
# No satisfying conditions were found, therefore the grow of the branch stops.
set_leaf_prediction(node, examples)
return
# Create two childrens for the node.
positive_child, negative_child = split_node(node, condition)
# List the training examples used by each children.
negative_examples = [example for example in examples if not condition(example)]
positive_examples = [example for example in examples if condition(example)]
# Continue the growth of the children.
grow_tree(negative_child, negative_examples)
grow_tree(positive_child, positive_examples)
Analicemos los pasos para entrenar un árbol de decisión en particular con más detalle.
Paso 1: Crea una raíz:
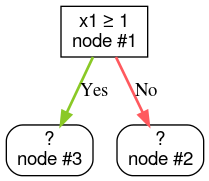
Paso 2: Expande el nodo n° 1. Se encontró la condición "x1 ≥ 1". Se crean dos nodos secundarios:
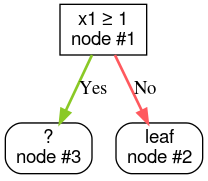
Paso 3: Expande el nodo 2. No se encontraron condiciones que satisfagan la búsqueda. Por lo tanto, convierte el nodo en una hoja:
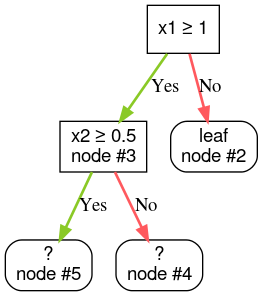
Paso 4: Expande el nodo 3. Se encontró la condición "x2 ≥ 0.5". Se crean dos nodos secundarios.
Existen otros métodos para desarrollar árboles de decisión. Una alternativa popular es optimizar los nodos de forma global en lugar de usar una estrategia de dividir y conquistar.
growing_strategy="BEST_FIRST_GLOBAL".
Para obtener más detalles, consulta
la documentación.
Según la cantidad y el tipo de atributos de entrada, la cantidad de condiciones posibles para un nodo determinado puede ser enorme, por lo general, infinita. Por ejemplo, dada una condición de umbral $\mathrm{feature}_i \geq t$, la combinación de todos los posibles valores de umbral para $t \in \mathbb{R}$ es infinita.
La rutina responsable de encontrar la mejor condición se denomina divisor. Debido a que deben probar muchas condiciones posibles, los divisores son el cuello de botella cuando se entrena un árbol de decisión.
La puntuación que maximiza el divisor depende de la tarea. Por ejemplo:
- La ganancia de información y el índice de Gini (ambos se analizan más adelante) suelen usarse para la clasificación.
- El error cuadrático medio se usa comúnmente para la regresión.
Existen muchos algoritmos de división, cada uno con diferentes niveles de compatibilidad con lo siguiente:
- El tipo de atributos, por ejemplo, numérico, categórico o de texto
- La tarea; por ejemplo, clasificación binaria, clasificación de clases múltiples o regresión
- Es el tipo de condición, por ejemplo, condición de límite, condición dentro del conjunto o condición oblicua.
- Los criterios de regularización, por ejemplo, divisores exactos o aproximados para condiciones de umbral
Además, existen variantes de divisores equivalentes con diferentes compensaciones en cuanto al uso de la memoria, el uso de la CPU, la distribución del procesamiento, etcétera.