Comme tous les modèles de machine learning supervisés, les arbres de décision sont entraînés pour expliquer au mieux un ensemble d'exemples d'entraînement. L'entraînement optimal d'un arbre de décision est un problème NP-difficile. Par conséquent, l'entraînement est généralement effectué à l'aide d'heuristiques, un algorithme d'apprentissage facile à créer qui fournit un arbre de décision non optimal, mais proche de l'optimum.
La plupart des algorithmes utilisés pour entraîner des arbres de décision fonctionnent avec une stratégie de division et de conquête gourmande. L'algorithme commence par créer un seul nœud (la racine) et développe de manière récursive et gourmande l'arbre de décision.
À chaque nœud, toutes les conditions possibles sont évaluées et notées. L'algorithme sélectionne la condition "meilleure", c'est-à-dire celle qui obtient le score le plus élevé. Pour l'instant, sachez simplement que le score est une métrique qui est corrélée à la tâche, et que des conditions sont sélectionnées pour maximiser cette métrique.
Par exemple, dans l'ensemble de données sur les manchots de l'Antarctique (utilisé pour les exemples de code plus tard dans ce cours), la plupart des manchots Adélie et à capuchon ont un bec de plus de 16 mm, tandis que la plupart des manchots gento sont dotés d'un bec plus petit. Par conséquent, la condition bill_length_mm ≥ 16 permet de faire des prédictions presque parfaites pour les pingouins Gentoo, mais ne permet pas de faire la distinction entre les pingouins Adélie et les pingouins à capuchon. L'algorithme sélectionnera probablement cette condition.

Figure 7. Première étape pour faire pousser un arbre.
L'algorithme se répète ensuite de manière récursive et indépendante sur les deux nœuds enfants. Si aucune condition n'est remplie, le nœud devient une feuille. La prédiction de la feuille est déterminée comme étant la valeur d'étiquette la plus représentative dans les exemples.
L'algorithme est le suivant:
def train_decision_tree(training_examples):
root = create_root() # Create a decision tree with a single empty root.
grow_tree(root, training_examples) # Grow the root node.
return root
def grow_tree(node, examples):
condition = find_best_condition(examples) # Find the best condition.
if condition is None:
# No satisfying conditions were found, therefore the grow of the branch stops.
set_leaf_prediction(node, examples)
return
# Create two childrens for the node.
positive_child, negative_child = split_node(node, condition)
# List the training examples used by each children.
negative_examples = [example for example in examples if not condition(example)]
positive_examples = [example for example in examples if condition(example)]
# Continue the growth of the children.
grow_tree(negative_child, negative_examples)
grow_tree(positive_child, positive_examples)
Examinons plus en détail les étapes d'entraînement d'un arbre de décision particulier.
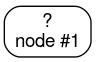
Étape 1:Créez une racine:
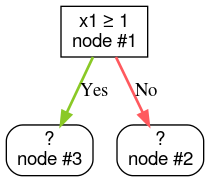
Étape 2:Développez le nœud 1. La condition "x1 ≥ 1" a été détectée. Deux nœuds enfants sont créés:
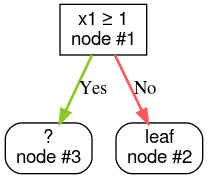
Étape 3:Développez le nœud 2. Aucune condition satisfaisante n'a été trouvée. Convertissez donc le nœud en feuille:
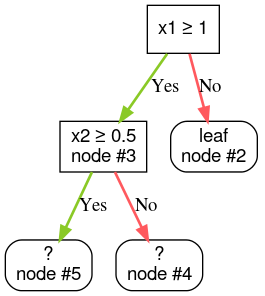
Étape 4:Développez le nœud 3. La condition "x2 ≥ 0,5" a été détectée. Deux nœuds enfants sont créés.
Il existe d'autres méthodes pour développer des arbres de décision. Une alternative populaire consiste à optimiser les nœuds de manière globale au lieu d'utiliser une stratégie de division et de conquête.
growing_strategy="BEST_FIRST_GLOBAL".
Pour en savoir plus, consultez la
documentation.
Selon le nombre et le type d'éléments géographiques d'entrée, le nombre de conditions possibles pour un nœud donné peut être énorme, généralement infini. Par exemple, étant donné une condition de seuil $\mathrm{feature}_i \geq t$, la combinaison de toutes les valeurs de seuil possibles pour $t \in \mathbb{R}$ est infinie.
La routine chargée de trouver la meilleure condition est appelée séparateur. Comme il doit tester de nombreuses conditions possibles, les séparateurs constituent le goulot d'étranglement lors de l'entraînement d'un arbre de décision.
Le score maximisé par le séparateur dépend de la tâche. Exemple :
- Le gain d'information et le coefficient de Gini (tous deux abordés plus loin) sont couramment utilisés pour la classification.
- L'erreur quadratique moyenne est couramment utilisée pour la régression.
Il existe de nombreux algorithmes de fractionnement, chacun étant compatible avec différents éléments:
- Type de caractéristiques (par exemple, numérique, catégorielle, texte)
- La tâche (par exemple, classification binaire, classification à classes multiples, régression)
- Type de condition (par exemple, condition de seuil, condition dans l'ensemble, condition oblique)
- Les critères de régularisation, par exemple des séparateurs exacts ou approchés pour les conditions de seuil
De plus, il existe des variantes d'un séparateur équivalent avec des compromis différents en termes d'utilisation de la mémoire, d'utilisation du processeur, de distribution du calcul, etc.
