隨機森林
透過集合功能整理內容
你可以依據偏好儲存及分類內容。
這是牛。
圖 19. 一頭牛。
1906 年，在英國舉辦了重量評估競賽。787 位參與者猜測牛的體重。個別猜測值的誤差中位數為 37 磅 (誤差 3.1%)。不過，猜測結果的整體中位數與牛的實際重量 (1,198 磅) 相差只有 9 磅，誤差率只有 0.7%。
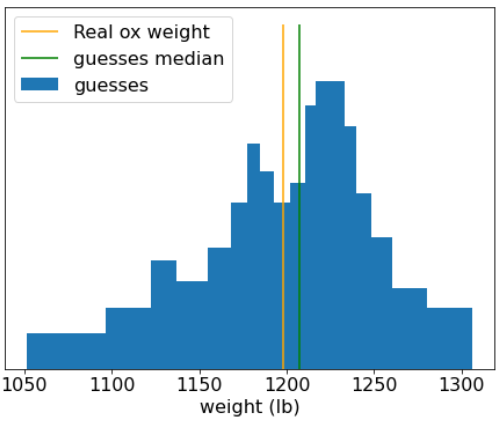
圖 20. 個別體重猜測值的直方圖。
這個軼事說明瞭「群眾智慧」：在某些情況下，集體意見可提供非常明智的判斷。
從數學角度來看，群眾智慧可透過中心極限定理建立模型：簡單來說，某個值與該值的 N 個雜訊估計值平均值之間的平方誤差，會隨著 1/N 因子趨近於零。不過，如果變數不獨立，變異數就會增加。
在機器學習中，集成是指一組模型，這些模型的預測結果會經過平均 (或以某種方式匯總)。如果集成模型彼此之間的差異足夠大，且個別模型的品質並未太差，集成模型的品質通常會優於個別模型。集成模型需要的訓練和推論時間，比單一模型還要長。畢竟您必須對多個模型 (而非單一模型) 執行訓練和推論。
非正式來說，為了讓集成模型發揮最佳效能，個別模型應保持獨立。舉例來說，由 10 個完全相同的模型組成的集成模型 (也就是完全不獨立) 不會比個別模型好。另一方面，強制讓模型保持獨立可能會讓模型變得更糟。要有效地進行集成，就必須在模型獨立性和子模型品質之間取得平衡。
除非另有註明，否則本頁面中的內容是採用創用 CC 姓名標示 4.0 授權，程式碼範例則為阿帕契 2.0 授權。詳情請參閱《Google Developers 網站政策》。Java 是 Oracle 和/或其關聯企業的註冊商標。
上次更新時間：2025-07-27 (世界標準時間)。
[null,null,["上次更新時間：2025-07-27 (世界標準時間)。"],[[["\u003cp\u003eThe "wisdom of the crowd" suggests that collective opinions can provide surprisingly accurate judgments, as demonstrated by a 1906 ox weight-guessing competition where the collective guess was remarkably close to the true weight.\u003c/p\u003e\n"],["\u003cp\u003eThis phenomenon can be explained by the Central Limit Theorem, which states that the average of multiple independent estimates tends to converge towards the true value.\u003c/p\u003e\n"],["\u003cp\u003eIn machine learning, ensembles leverage this principle by combining predictions from multiple models, improving overall accuracy when individual models are sufficiently diverse and reasonably accurate.\u003c/p\u003e\n"],["\u003cp\u003eWhile ensembles require more computational resources, their enhanced predictive performance often outweighs the added cost, especially when individual models are carefully selected and combined.\u003c/p\u003e\n"],["\u003cp\u003eAchieving optimal ensemble performance involves striking a balance between ensuring model independence to avoid redundant predictions and maintaining the individual quality of sub-models for overall accuracy.\u003c/p\u003e\n"]]],[],null,["# Random Forest\n\n\u003cbr /\u003e\n\nThis is an Ox.\n\n\n**Figure 19. An ox.**\n\n\u003cbr /\u003e\n\nIn 1906, a [weight judging competition was held in\nEngland](https://www.nature.com/articles/075450a0.pdf).\n787 participants guessed the weight of an ox. The median *error* of individual\nguesses was 37 lb (an error of 3.1%). However, the overall median of the\nguesses was only 9 lb away from the real weight of the ox (1198 lb), which was\nan error of only 0.7%.\n\n**Figure 20. Histogram of individual weight guesses.**\n\nThis anecdote illustrates the\n[Wisdom of the crowd](/machine-learning/glossary#wisdom_of_the_crowd): *In\ncertain situations, collective opinion provides very good judgment.*\n\nMathematically, the wisdom of the crowd can be modeled with the\n[Central limit theorem](https://wikipedia.org/wiki/Central_limit_theorem):\nInformally, the squared error between a value and the average of N noisy\nestimates of this value tends to zero with a 1/N factor.\nHowever, if the variables are not independent, the variance is greater.\n\nIn machine learning, an\n**[ensemble](/machine-learning/glossary#ensemble)** is a collection of models\nwhose predictions are averaged (or aggregated in some way). If the ensemble\nmodels are different enough without being too bad individually, the quality of\nthe ensemble is generally better than the quality of each of the individual\nmodels. An ensemble requires more training and inference time than a single\nmodel. After all, you have to perform training and inference on multiple models\ninstead of a single model.\n\nInformally, for an ensemble to work best, the individual models should be\nindependent. As an illustration, an ensemble composed of 10 of the exact same\nmodels (that is, not independent at all) won't be better than the individual\nmodel. On the other hand, forcing models to be independent could mean making\nthem worse. Effective ensembling requires finding the balance between model\nindependence and the quality of its sub-models."]]
