Random Forest
จัดทุกอย่างให้เป็นระเบียบอยู่เสมอด้วยคอลเล็กชัน
บันทึกและจัดหมวดหมู่เนื้อหาตามค่ากำหนดของคุณ
นี่คือวัว
รูปที่ 19 วัว
ในปี 1906 มีการจัดการแข่งขันการตัดสินน้ำหนักในอังกฤษ
ผู้เข้าร่วม 787 คนคาดเดาน้ำหนักของวัว ข้อผิดพลาดมัธยฐานของการคาดคะเนแต่ละรายการคือ 16.8 กก. (ข้อผิดพลาด 3.1%) อย่างไรก็ตาม ค่ามัธยฐานโดยรวมของการคาดคะเนอยู่ห่างจากน้ำหนักจริงของวัว (1,198 ปอนด์) เพียง 4 กก.ซึ่งมีความคลาดเคลื่อนเพียง 0.7%
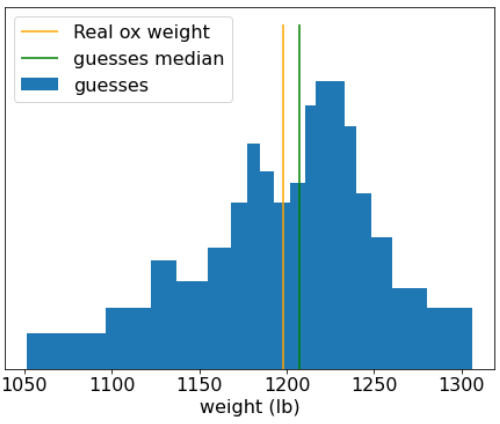
รูปที่ 20 ฮิสโตแกรมของการคาดคะเนน้ำหนักแต่ละรายการ
เกร็ดเล็กเกร็ดน้อยนี้แสดงให้เห็นถึงภูมิปัญญาของมวลชน: ในบางสถานการณ์ ความคิดเห็นของมวลชนจะให้การตัดสินที่ดีมาก
ในทางคณิตศาสตร์ เราสามารถประมาณภูมิปัญญาของมวลชนได้ด้วยทฤษฎีบททางสถิติส่วนกลาง ดังนี้
โดยทั่วไปแล้ว ความคลาดเคลื่อนกำลังสองระหว่างค่าหนึ่งๆ กับค่าเฉลี่ยของค่าประมาณ N ค่าที่มีสัญญาณรบกวนสำหรับค่านี้จะมีแนวโน้มเป็น 0 โดยมีปัจจัย 1/N
อย่างไรก็ตาม หากตัวแปรไม่อิสระ ค่าความแปรปรวนจะมากกว่า
ในแมชชีนเลิร์นนิง ชุดค่าผสมคือคอลเล็กชันโมเดลที่มีการคาดการณ์โดยเฉลี่ย (หรือรวบรวมข้อมูลด้วยวิธีใดวิธีหนึ่ง) หากโมเดลการรวมมีความแตกต่างกันมากพอโดยไม่แย่เกินไป โดยทั่วไปแล้วคุณภาพของการรวมจะดีกว่าคุณภาพของโมเดลแต่ละรายการ การรวมกลุ่มต้องใช้เวลาในการฝึกและเวลาในการอนุมานมากกว่าโมเดลเดียว ท้ายที่สุดแล้ว คุณต้องทำการเทรนและการอนุมานกับโมเดลหลายรายการแทนที่จะทำกับโมเดลเดียว
โดยทั่วไปแล้ว โมเดลแต่ละรายการควรเป็นอิสระต่อกันเพื่อให้การรวมโมเดลทำงานได้ดีที่สุด ตัวอย่างเช่น ชุดค่าผสมที่ประกอบด้วยโมเดลเดียวกันทั้งหมด 10 รายการ (กล่าวคือ ไม่ได้เป็นอิสระเลย) จะมีประสิทธิภาพไม่ดีกว่าโมเดลแต่ละรายการ ในทางกลับกัน การบังคับให้โมเดลเป็นแบบอิสระอาจทำให้โมเดลทำงานได้แย่ลง การรวมกลุ่มที่มีประสิทธิภาพต้องอาศัยการหาจุดสมดุลระหว่างความเป็นอิสระของโมเดลกับคุณภาพของโมเดลย่อย
เนื้อหาของหน้าเว็บนี้ได้รับอนุญาตภายใต้ใบอนุญาตที่ต้องระบุที่มาของครีเอทีฟคอมมอนส์ 4.0 และตัวอย่างโค้ดได้รับอนุญาตภายใต้ใบอนุญาต Apache 2.0 เว้นแต่จะระบุไว้เป็นอย่างอื่น โปรดดูรายละเอียดที่นโยบายเว็บไซต์ Google Developers Java เป็นเครื่องหมายการค้าจดทะเบียนของ Oracle และ/หรือบริษัทในเครือ
อัปเดตล่าสุด 2025-07-27 UTC
[null,null,["อัปเดตล่าสุด 2025-07-27 UTC"],[[["\u003cp\u003eThe "wisdom of the crowd" suggests that collective opinions can provide surprisingly accurate judgments, as demonstrated by a 1906 ox weight-guessing competition where the collective guess was remarkably close to the true weight.\u003c/p\u003e\n"],["\u003cp\u003eThis phenomenon can be explained by the Central Limit Theorem, which states that the average of multiple independent estimates tends to converge towards the true value.\u003c/p\u003e\n"],["\u003cp\u003eIn machine learning, ensembles leverage this principle by combining predictions from multiple models, improving overall accuracy when individual models are sufficiently diverse and reasonably accurate.\u003c/p\u003e\n"],["\u003cp\u003eWhile ensembles require more computational resources, their enhanced predictive performance often outweighs the added cost, especially when individual models are carefully selected and combined.\u003c/p\u003e\n"],["\u003cp\u003eAchieving optimal ensemble performance involves striking a balance between ensuring model independence to avoid redundant predictions and maintaining the individual quality of sub-models for overall accuracy.\u003c/p\u003e\n"]]],[],null,["# Random Forest\n\n\u003cbr /\u003e\n\nThis is an Ox.\n\n\n**Figure 19. An ox.**\n\n\u003cbr /\u003e\n\nIn 1906, a [weight judging competition was held in\nEngland](https://www.nature.com/articles/075450a0.pdf).\n787 participants guessed the weight of an ox. The median *error* of individual\nguesses was 37 lb (an error of 3.1%). However, the overall median of the\nguesses was only 9 lb away from the real weight of the ox (1198 lb), which was\nan error of only 0.7%.\n\n**Figure 20. Histogram of individual weight guesses.**\n\nThis anecdote illustrates the\n[Wisdom of the crowd](/machine-learning/glossary#wisdom_of_the_crowd): *In\ncertain situations, collective opinion provides very good judgment.*\n\nMathematically, the wisdom of the crowd can be modeled with the\n[Central limit theorem](https://wikipedia.org/wiki/Central_limit_theorem):\nInformally, the squared error between a value and the average of N noisy\nestimates of this value tends to zero with a 1/N factor.\nHowever, if the variables are not independent, the variance is greater.\n\nIn machine learning, an\n**[ensemble](/machine-learning/glossary#ensemble)** is a collection of models\nwhose predictions are averaged (or aggregated in some way). If the ensemble\nmodels are different enough without being too bad individually, the quality of\nthe ensemble is generally better than the quality of each of the individual\nmodels. An ensemble requires more training and inference time than a single\nmodel. After all, you have to perform training and inference on multiple models\ninstead of a single model.\n\nInformally, for an ensemble to work best, the individual models should be\nindependent. As an illustration, an ensemble composed of 10 of the exact same\nmodels (that is, not independent at all) won't be better than the individual\nmodel. On the other hand, forcing models to be independent could mean making\nthem worse. Effective ensembling requires finding the balance between model\nindependence and the quality of its sub-models."]]
