C'est un bœuf.
Figure 19. Un bœuf.
En 1906, un compétition d'évaluation de poids s'est tenue en Angleterre. 787 participants ont deviné le poids d'un bœuf. L'erreur médiane de requêtes individuelles était de 37 lb (erreur de 3,1%). Cependant, la médiane globale des digues n'était qu'à 9 lb du poids réel du bœuf (1 198 lb), soit une erreur de 0,7 % seulement.
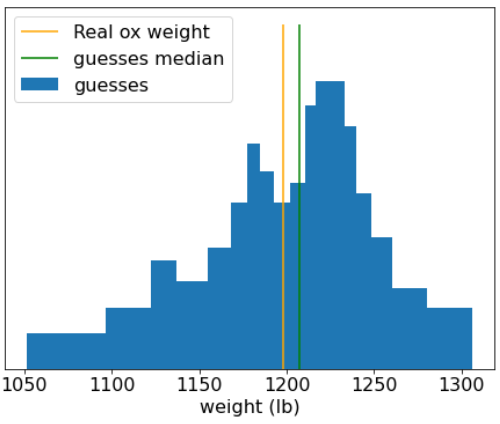
Figure 20. Histogramme des estimations de poids individuelles.
Cette anecdote illustre la sagesse des foules : Dans certaines situations, l'opinion collective est très juste.
Mathématiquement, la sagesse de la foule peut être modélisée à l'aide du théorème central : de manière formelle, l'erreur quadratique moyenne entre une valeur et la moyenne de N estimations bruyantes de cette valeur tend à zéro avec un facteur de 1/N. Toutefois, si les variables ne sont pas indépendantes, la variance est plus importante.
En machine learning, un ensemble est un ensemble de modèles dont la moyenne est calculée ou agrégée d'une manière ou d'une autre. Si les modèles d'ensemble sont suffisamment différents sans être trop mauvais individuellement, la qualité de l'ensemble est généralement meilleure que celle de chacun des modèles. Un ensemble nécessite plus de temps d'entraînement et d'inférence qu'un seul modèle. Après tout, vous devez effectuer l'entraînement et l'inférence sur plusieurs modèles au lieu d'un seul.
De manière informelle, pour qu'un ensemble fonctionne de manière optimale, les modèles individuels doivent être indépendants. À titre d'exemple, un ensemble composé de 10 mêmes modèles (c'est-à-dire totalement indépendants) ne sera pas meilleur que le modèle individuel. D'un autre côté, forcer des modèles pour qu'ils soient indépendants pourrait les empirer. Une inférence efficace nécessite de trouver l'équilibre entre l'indépendance du modèle et la qualité de ses sous-modèles.