דף זה תורגם על ידי Cloud Translation API.

עצי החלטות משופרים בצבע הדרגתי

בדף הזה
הצטמקות

בדומה ל-bagging ול-boosting, שיפור שיפוע הוא שיטת עבודה שמופעלת על גבי אלגוריתם אחר של למידת מכונה. באופן לא רשמי, שיפור גרדיאנטים כרוך בשני סוגים של מודלים:

מודל 'חלש' של למידת מכונה, שהוא בדרך כלל עץ החלטות.
מודל 'חזק' של למידת מכונה, שמורכב מכמה מודלים חלשים.

בשיטת ה-Gradient Boosting, בכל שלב מתבצע אימון של מודל חלש חדש כדי לחזות את 'השגיאה' של המודל החזק הנוכחי (שנקרא תגובה פסאודו). בהמשך נפרט על 'שגיאה'. בשלב הזה, נניח ש'שגיאה' היא ההבדל בין התחזית לבין תווית רגרסיבית. לאחר מכן, המודל החלש (כלומר 'השגיאה') מתווסף למודל החזק עם סימן שלילי כדי לצמצם את השגיאה של המודל החזק.

שיפור הרגישות לגרדיאנט הוא תהליך איטרטיבי. בכל חזרה על התהליך, הנוסחה הבאה מופעלת:

F_{i + 1} = F_{i} - f_{i}

$F_{i+1} = F_i - f_i$

where:

$F_i$ הוא המודל החזק בשלב $i$ .
$f_i$ הוא הדגם החלש בשלב $i$ .

הפעולה הזו חוזרת על עצמה עד לעמידה בקריטריון עצירה, כמו מספר סבבים מקסימלי או אם המודל (החזק) מתחיל להתאים יותר מדי, כפי שנמדד במערך נתונים נפרד לצורך אימות.

נציג דוגמה ל-Gradient Boosting במערך נתונים פשוט של רגרסיה, שבו:

המטרה היא לחזות את הערך של $y$ לפי הערך של $x$ .
מודל החזק מאופשר כקבוע אפס: $F_0(x) = 0$ .

# Simplified example of regressive gradient boosting.

y = ... # the labels
x = ... # the features

strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.

for i in range(num_iters):

    # Error of the strong model
    error = strong_predictions - y

    # The weak model is a decision tree (see CART chapter)
    # without pruning and a maximum depth of 3.
    weak_model = tfdf.keras.CartModel(
        task=tfdf.keras.Task.REGRESSION,
        validation_ratio=0.0,
        max_depth=3)
    weak_model.fit(x=x, y=error)

    strong_model.append(weak_model)

    weak_predictions = weak_model.predict(x)[:,0]

    strong_predictions -= weak_predictions

נשתמש בקוד הזה במערך הנתונים הבא:

תרשים של ערכי סף (ground truth) למאפיין אחד, x, ולתווית שלו, y. התרשים הוא סדרה של גלי סינוס שהתחזקו במקצת.

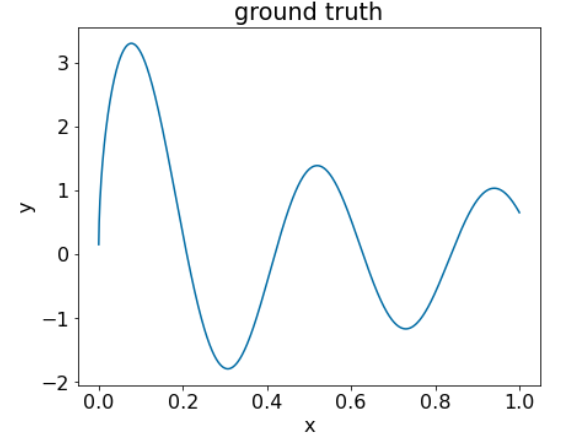
איור 25. מערך נתונים רגרסיבי סינתטי עם תכונה מספרית אחת.

לפניכם שלושה תרשימים אחרי האיטרציה הראשונה של אלגוריתם ה-gradient boosting:

שלוש תוכניות. בתרשים הראשון מוצגת התחזית של המודל החזק, שהיא קו ישר עם שיפוע 0 ו-y-intercept 0. בתרשים השני מוצגת השגיאה של המודל החזק, שהיא סדרה של גלי סינוס. בתרשים השלישי מוצגת התחזית של המודל החלש, שהיא קבוצה של גלים ריבועיים.

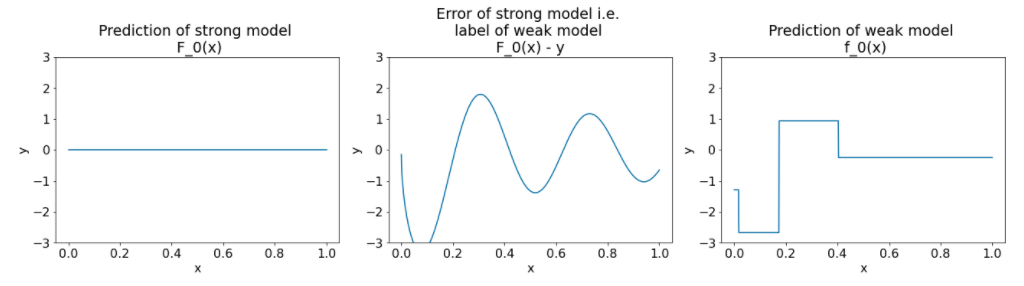
איור 26. שלושה תרשימים אחרי המחזור הראשון.

שימו לב לנקודות הבאות לגבי התרשימים באיור 26:

בתרשים הראשון מוצגות התחזיות של המודל החזק, שכרגע תמיד הן 0.
בתרשים השני מוצגת השגיאה, שהיא התווית של המודל החלש.
בתרשים השלישי מוצג המודל החלש.

המודל החלש הראשון לומד ייצוג גס של התווית, ומתמקד בעיקר בחלק הימני של מרחב המאפיינים (החלק עם השונות הגדולה ביותר, ולכן עם השגיאה הגדולה ביותר במודל הקבוע השגוי).

בהמשך מוצגים אותם תרשימים לגרסה אחרת של האלגוריתם:

שלוש תוכניות. בתרשים הראשון מוצגת התחזית של המודל החזק, שהיא ההופכית של התחזית של המודל החלש שמוצגת באיור הקודם. בתרשים השני מוצגת השגיאה של המודל החזק, שהיא קבוצה רועשת של גלי סינוס. בתרשים השלישי מוצגת התחזית של המודל החלש, שהיא כמה גלים ריבועיים.

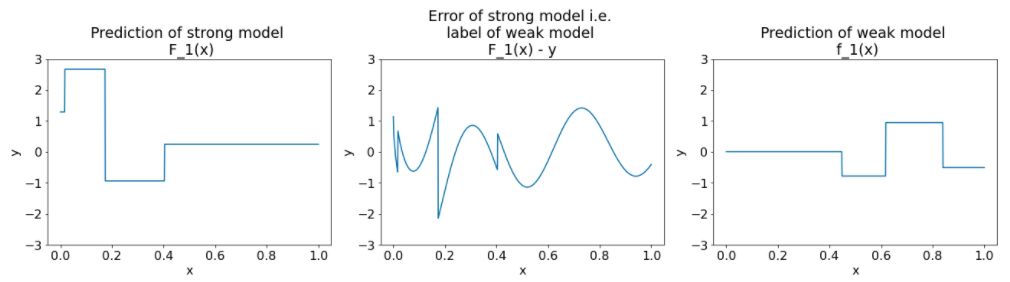
איור 27. שלוש תצוגות תרשים אחרי המחזור השני.

שימו לב לנקודות הבאות לגבי התרשימים בתרשים 27:

המודל החזק מכיל עכשיו את החיזוי של המודל החלש מהאיטרציה הקודמת.
השגיאה החדשה של המודל החזק קטנה יותר.
התחזית החדשה של המודל החלש מתמקדת עכשיו בחלק הימני של מרחב המאפיינים.

אנחנו מריצים את האלגוריתם ב-8 חזרות נוספות:

בתרשים אפשר לראות שהמודל החזק מתקרב בהדרגה לאמת, בעוד שהחיזוי של המודל החלש הולך ונעשה חלש יותר.

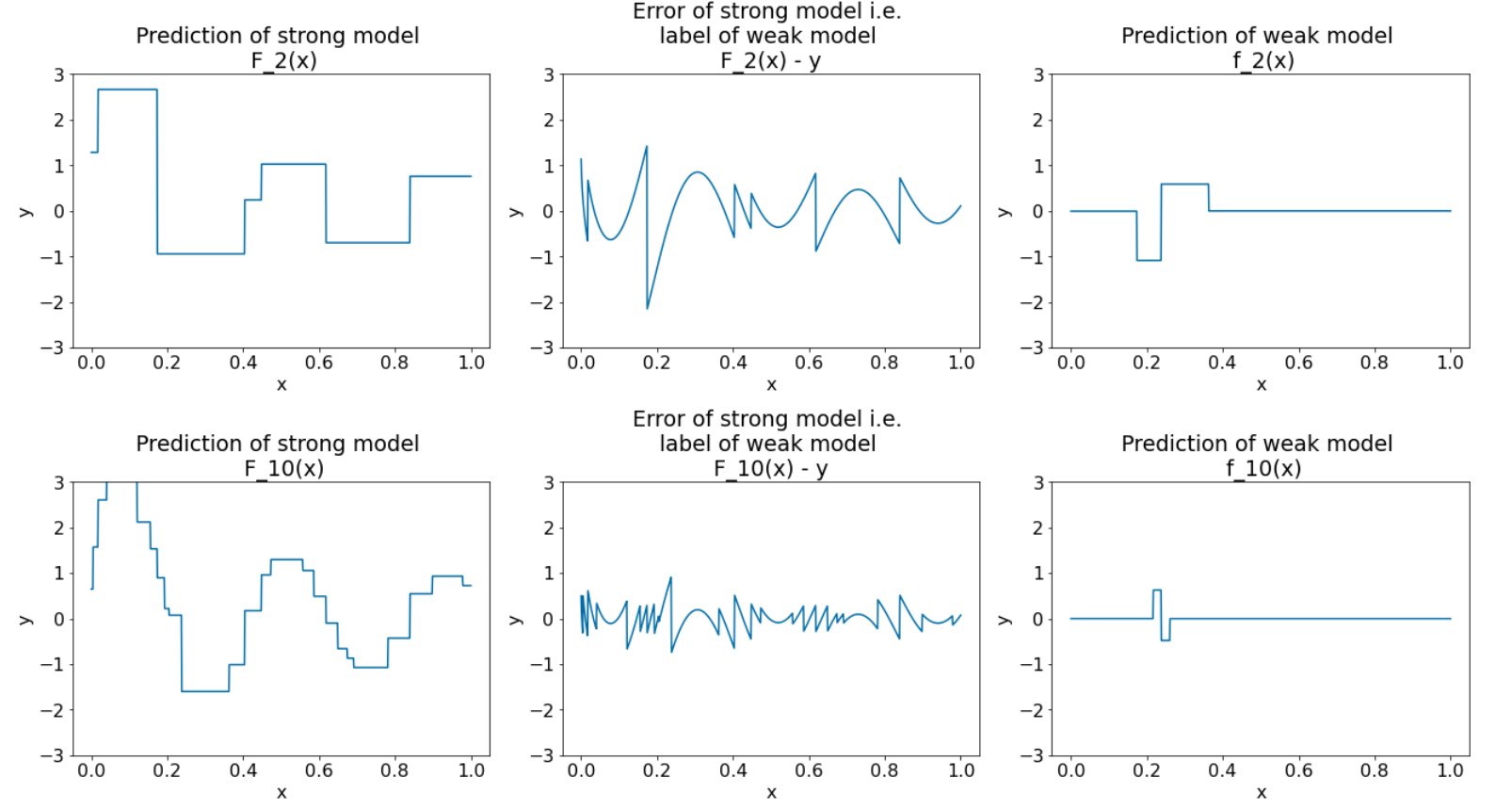
איור 28. שלוש תצוגות גרפיות אחרי האיטרציה השלישית ואחרי האיטרציה העשירית.

שימו לב שבאיור 28, התחזית של המודל החזק מתחילה להיראות כמו התרשים של מערך הנתונים.

התרשימים האלה מדגימים את אלגוריתם ה-gradient boosting באמצעות עצי החלטה כמודלים למידה חלשים. השילוב הזה נקרא עצים משופרים (החלטות) של שיפוע.

התרשימים הקודמים מראים את המהות של שיפור שיפוע (gradient boosting). עם זאת, בדוגמה הזו חסרות שתי הפעולות הבאות בעולם האמיתי:

הצמצום
אופטימיזציה של ערכי עלים באמצעות שלב אחד של שיטת ניוטון

הצטמקות

המודל החלש $f_i$ מוכפל בערך קטן $\nu$ (לדוגמה, $\nu = 0.1$ ) לפני שהוא מתווסף למודל החזק $F_i$ . הערך הקטן הזה נקרא צמצום. במילים אחרות, במקום להשתמש בנוסחה הבאה בכל חזרה:

F_{i + 1} = F_{i} - f_{i}

$F_{i+1} = F_i - f_i$

בכל חזרה על התהליך נעשה שימוש בנוסחה הבאה:

F_{i + 1} = F_{i} - ν f_{i}

$F_{i+1} = F_i - \nu f_i$

הצטמקות ב-gradient boosting דומה לשיעור הלמידה ברשתות נוירונים. באמצעות הצטמקות אפשר לקבוע את מהירות הלמידה של המודל החזק, וכך להגביל את ההתאמה היתרה. כלומר, ערך הצטמקות קרוב יותר ל-0.0 מפחית את ההתאמה היתרה יותר מערך הצטמקות קרוב יותר ל-1.0.

בקוד שלמעלה, הצמצום יוטמע באופן הבא:

shrinkage = 0.1   # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions

נושאים אחרים

האלגוריתם לשיפור הדרגה (אופציונלי)