Подобно пакетированию и повышению, повышение градиента — это методология, применяемая поверх другого алгоритма машинного обучения. Неофициально повышение градиента включает в себя два типа моделей:
- «слабая» модель машинного обучения, которая обычно представляет собой дерево решений.
- «сильная» модель машинного обучения, состоящая из нескольких слабых моделей.
При повышении градиента на каждом этапе новая слабая модель обучается для прогнозирования «ошибки» текущей сильной модели (которая называется псевдоответом ). Мы подробно опишем «ошибку» позже. А пока предположим, что «ошибка» — это разница между прогнозом и регрессивной меткой. Слабая модель (то есть «ошибка») затем добавляется к сильной модели с отрицательным знаком, чтобы уменьшить ошибку сильной модели.
Повышение градиента является итеративным. Каждая итерация вызывает следующую формулу:
\[ F_{i+1} = F_i - f_i \]
где:
- $F_i$ — сильная модель на шаге $i$.
- $f_i$ — слабая модель на шаге $i$.
Эта операция повторяется до тех пор, пока не будет выполнен критерий остановки, например максимальное количество итераций или если (сильная) модель не начнет переобучаться, как измерено в отдельном наборе проверочных данных.
Давайте проиллюстрируем повышение градиента на простом наборе данных регрессии, где:
- Цель состоит в том, чтобы предсказать $y$ из $x$.
- Сильная модель инициализируется нулевой константой: $F_0(x) = 0$.
# Simplified example of regressive gradient boosting.
y = ... # the labels
x = ... # the features
strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.
for i in range(num_iters):
# Error of the strong model
error = strong_predictions - y
# The weak model is a decision tree (see CART chapter)
# without pruning and a maximum depth of 3.
weak_model = tfdf.keras.CartModel(
task=tfdf.keras.Task.REGRESSION,
validation_ratio=0.0,
max_depth=3)
weak_model.fit(x=x, y=error)
strong_model.append(weak_model)
weak_predictions = weak_model.predict(x)[:,0]
strong_predictions -= weak_predictions
Давайте применим этот код к следующему набору данных:
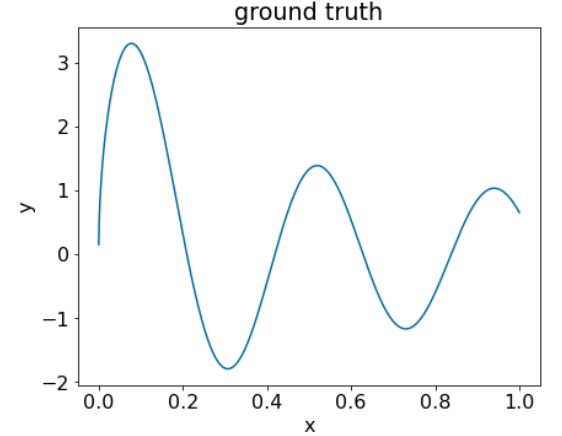
Рисунок 25. Синтетический регрессионный набор данных с одним числовым признаком.
Вот три графика после первой итерации алгоритма повышения градиента:
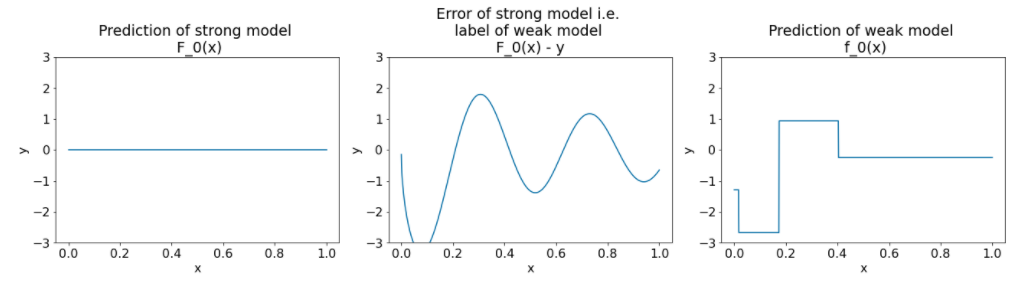
Рисунок 26. Три графика после первой итерации.
Обратите внимание на следующие моменты относительно графиков на рисунке 26:
- Первый график показывает прогнозы сильной модели, которая в настоящее время всегда равна 0.
- Второй график показывает ошибку, которая является меткой слабой модели.
- Третий график показывает слабую модель.
Первая слабая модель изучает грубое представление метки и в основном фокусируется на левой части пространства признаков (часть с наибольшим разнообразием и, следовательно, наибольшим количеством ошибок для постоянной неправильной модели).
Ниже приведены те же графики для другой итерации алгоритма:
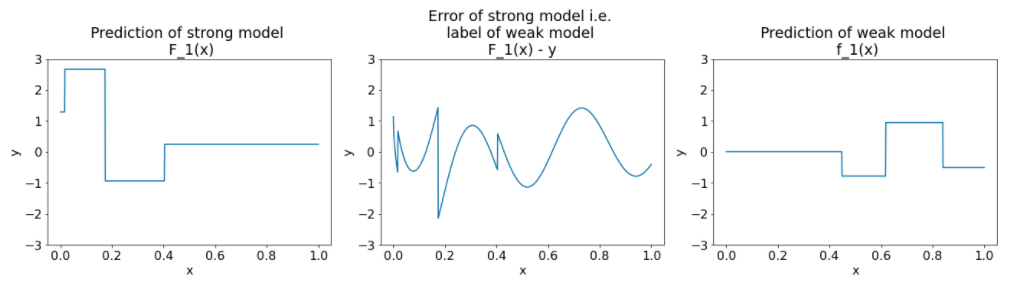
Рисунок 27. Три графика после второй итерации.
Обратите внимание на графики на рисунке 27:
- Сильная модель теперь содержит прогноз слабой модели предыдущей итерации.
- Новая ошибка сильной модели немного меньше.
- Новое предсказание слабой модели теперь фокусируется на правой части пространства признаков.
Прогоняем алгоритм еще на 8 итераций:
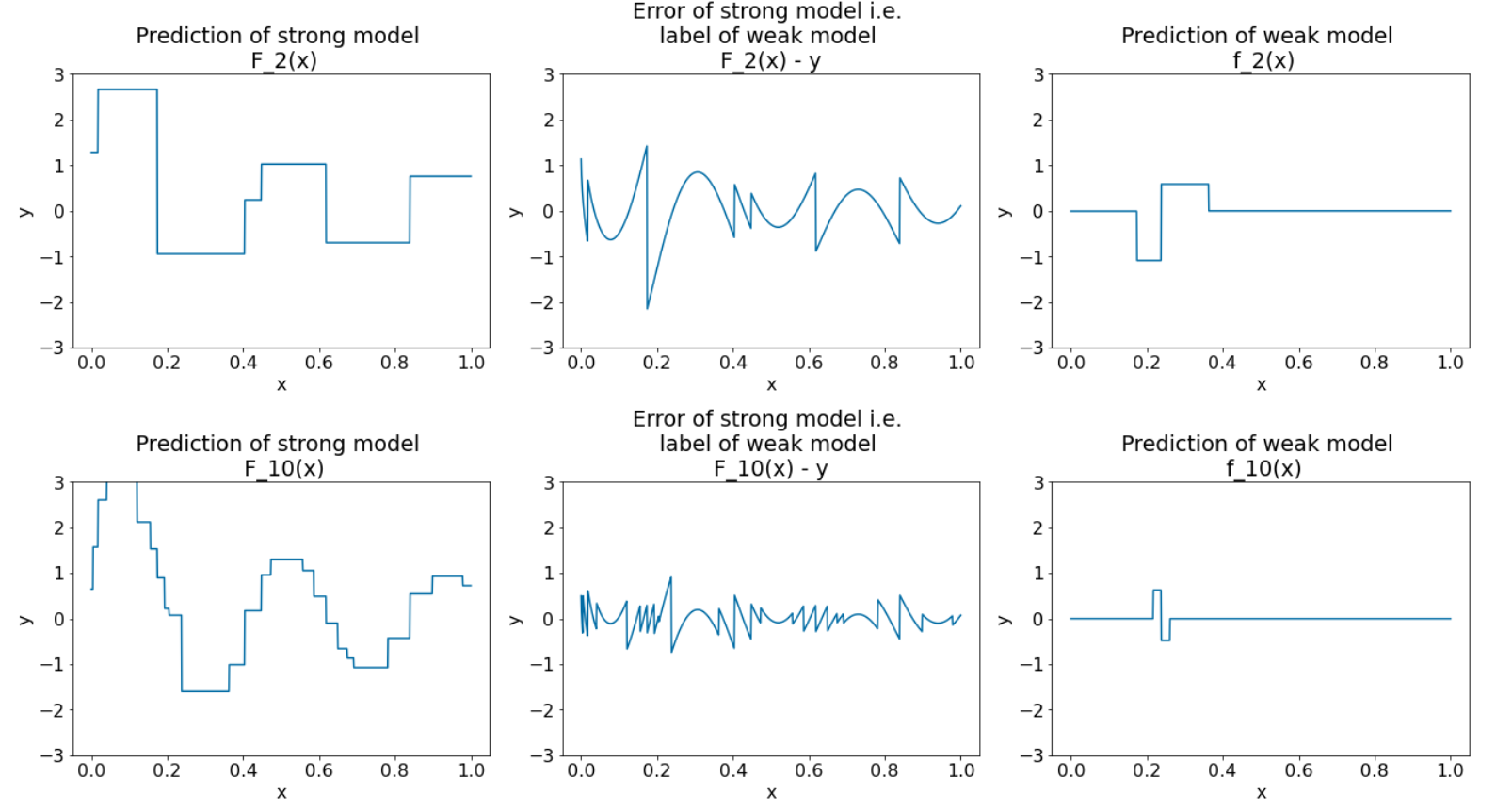
Рисунок 28. Три графика после третьей и десятой итерации.
Обратите внимание, что на рисунке 28 прогноз сильной модели начинает напоминать график набора данных .
Эти рисунки иллюстрируют алгоритм повышения градиента, использующий деревья решений в качестве слабых обучающихся. Эта комбинация называется деревьями решений с градиентным усилением .
Предыдущие графики показывают суть повышения градиента. Однако в этом примере отсутствуют следующие две реальные операции:
- Усадка
- Оптимизация значений листьев за один шаг метода Ньютона
Усадка
Слабая модель $f_i$ перед добавлением к сильной модели $F_i$ умножается на небольшое значение $\nu$ (например, $\nu = 0,1$). Эта небольшая величина называется усадкой . Другими словами, вместо каждой итерации используется следующая формула:
\[ F_{i+1} = F_i - f_i \]
Каждая итерация использует следующую формулу:
\[ F_{i+1} = F_i - \nu f_i \]
Сокращение при повышении градиента аналогично скорости обучения в нейронных сетях. Усадка контролирует скорость обучения сильной модели, что помогает ограничить переобучение. То есть значение усадки ближе к 0,0 уменьшает переобучение больше, чем значение усадки ближе к 1,0.
В нашем коде выше сжатие будет реализовано следующим образом:
shrinkage = 0.1 # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions
