與袋裝法和提升法一樣,梯度提升法是一種在其他機器學習演算法之上套用的做法。非正式的梯度提升包含兩種模型:
- 使用「弱」的機器學習模型,通常是決策樹。
- 由多個弱機器學習模型組成的「強大」機器學習模型。
在梯度提升法中,每個步驟都會訓練新的弱模型,以預測目前強模型的「錯誤」(稱為擬應答)。我們稍後會詳細說明「錯誤」。目前假設「誤差」是預測值和回歸標籤之間的差異。然後將弱模型 (即「錯誤」) 加上負號,再加入強模型,藉此減少強模型的錯誤。
梯度提升是一種疊代演算法。每個迭代都會叫用下列公式:
\[ F_{i+1} = F_i - f_i \]
其中:
- $F_i$ 是步驟 $i$ 的強大模型。
- $f_i$ 是步驟 $i$ 的弱模型。
這個作業會重複執行,直到符合停止條件為止,例如最大疊代次數,或是在個別驗證資料集上測量時,(強大) 模型開始過度擬合。
我們將以簡單的迴歸資料集說明梯度提升法,如下所示:
- 目標是根據 $x$ 預測 $y$。
- 強力模型會初始化為零常數:$F_0(x) = 0$。
# Simplified example of regressive gradient boosting.
y = ... # the labels
x = ... # the features
strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.
for i in range(num_iters):
# Error of the strong model
error = strong_predictions - y
# The weak model is a decision tree (see CART chapter)
# without pruning and a maximum depth of 3.
weak_model = tfdf.keras.CartModel(
task=tfdf.keras.Task.REGRESSION,
validation_ratio=0.0,
max_depth=3)
weak_model.fit(x=x, y=error)
strong_model.append(weak_model)
weak_predictions = weak_model.predict(x)[:,0]
strong_predictions -= weak_predictions
我們來在下列資料集上套用這段程式碼:
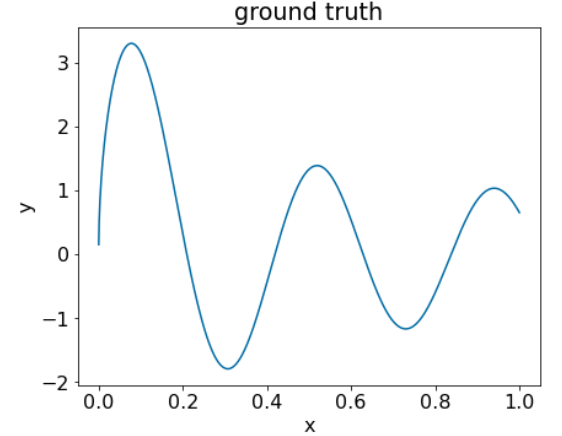
圖 25. 含有一個數值特徵的合成回歸資料集。
以下是梯度提升演算法第一次迭代後的三個圖表:
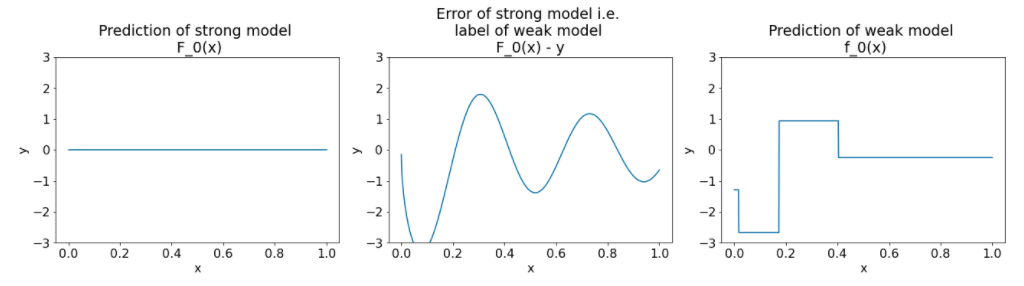
圖 26. 第一次迭代後的三個圖表。
請注意圖 26 中圖表的下列事項:
- 第一個圖表顯示強大模型的預測結果,目前一律為 0。
- 第二個圖表顯示錯誤,也就是弱模型的標籤。
- 第三個圖表顯示弱模型。
第一個弱模型會學習標籤的大致表示方式,主要著重於特徵空間的左側部分 (變化最多的部分,因此對常數錯誤模型的誤差最大)。
以下是另一個演算法疊代作業的相同圖表:
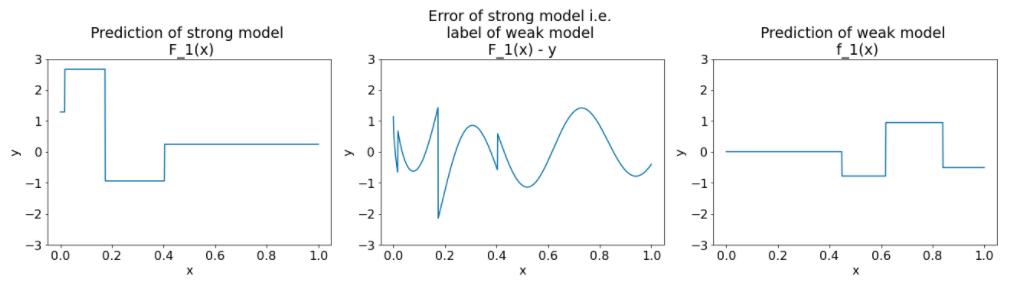
圖 27. 第二次迭代後的三個區塊。
請注意圖 27 中圖表的下列事項:
- 強模型現在包含上一個迭代中弱模型的預測結果。
- 強大模型的新誤差值會稍微縮小。
- 弱模型的新預測結果現在著重於特徵空間的右側。
我們執行演算法,進行 8 次疊代:
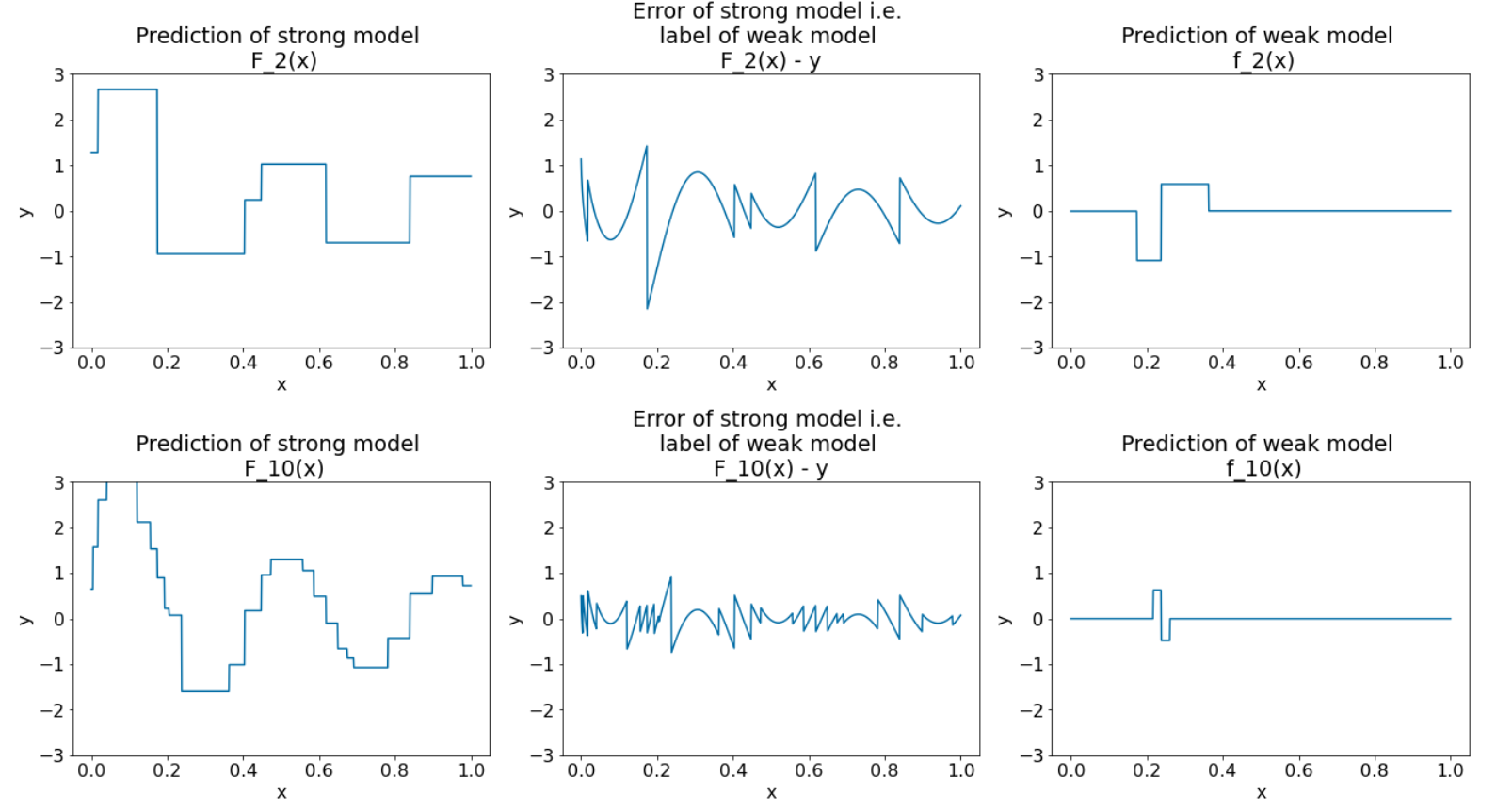
圖 28. 第三次和第十次疊代後的三個圖表。
請注意,在圖 28 中,強大模型的預測結果開始類似資料集的圖表。
這些圖表說明梯度提升演算法使用決策樹做為弱學習器。這種組合稱為梯度提升 (決策) 樹。
上述圖表顯示梯度提升法的精髓。不過,這個範例缺少以下兩個實際操作:
- 收縮
- 使用牛頓方法的一個步驟,對葉節值進行最佳化
縮水
弱模型 $f_i$ 會先乘上小值 $\nu$ (例如 $\nu = 0.1$),再加進強模型 $F_i$。這個小值稱為收縮。換句話說,不要在每次疊代中使用下列公式:
\[ F_{i+1} = F_i - f_i \]
每個迭代都會使用以下公式:
\[ F_{i+1} = F_i - \nu f_i \]
梯度提升中的收縮與類神經網路中的學習率類似。收縮功能會控制強大模型的學習速度,有助於限制過度擬合。也就是說,收縮值越接近 0.0,越能減少過度擬合,而收縮值越接近 1.0,越無法減少過度擬合。
在上述程式碼中,縮減功能的實作方式如下:
shrinkage = 0.1 # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions
