バギングやブーストと同様に、勾配ブーストは別の ML アルゴリズムの上に適用される手法です。非公式には、勾配ブーストには次の 2 種類のモデルが関与しています。
- 「弱い」機械学習モデル(通常はディシジョン ツリー)。
- 複数の弱いモデルで構成される「強力な」機械学習モデル。
勾配ブーストでは、各ステップで新しい弱いモデルがトレーニングされ、現在の強いモデルの「エラー」(疑似レスポンス)を予測します。「エラー」については後で詳しく説明します。ここでは、予測と回帰ラベルの差を「誤差」とします。弱いモデル(「エラー」)は、負の符号で強いモデルに追加され、強いモデルのエラーを減らします。
勾配ブースティングは反復処理です。各反復処理で、次の式が呼び出されます。
\[ F_{i+1} = F_i - f_i \]
ここで
- $F_i$ はステップ $i$ の強力なモデルです。
- $f_i$ はステップ $i$ の弱いモデルです。
このオペレーションは、最大イテレーション回数などの停止条件が満たされるか、別の検証データセットで測定された(強力な)モデルが過剰適合し始めるまで繰り返されます。
次の単純な回帰データセットで、勾配ブーストを説明しましょう。
- 目的は、$x$ から $y$ を予測することです。
- 強力なモデルは、ゼロ定数($F_0(x) = 0$)に初期化されます。
# Simplified example of regressive gradient boosting.
y = ... # the labels
x = ... # the features
strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.
for i in range(num_iters):
# Error of the strong model
error = strong_predictions - y
# The weak model is a decision tree (see CART chapter)
# without pruning and a maximum depth of 3.
weak_model = tfdf.keras.CartModel(
task=tfdf.keras.Task.REGRESSION,
validation_ratio=0.0,
max_depth=3)
weak_model.fit(x=x, y=error)
strong_model.append(weak_model)
weak_predictions = weak_model.predict(x)[:,0]
strong_predictions -= weak_predictions
このコードを次のデータセットに適用してみましょう。
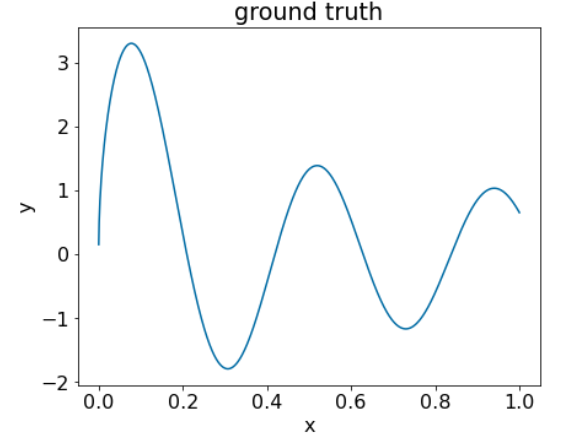
図 25. 1 つの数値特徴量を含む合成回帰データセット。
勾配ブースト アルゴリズムの最初の反復処理後の 3 つのプロットは次のとおりです。
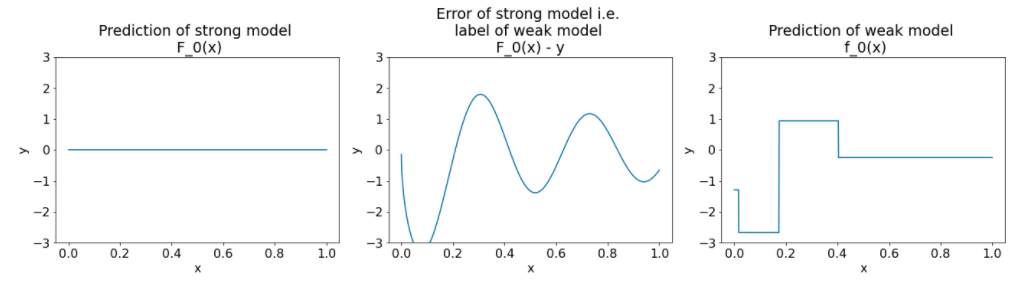
図 26. 最初の反復処理後の 3 つのプロット。
図 26 のグラフについて、次の点に注意してください。
- 最初のプロットは、強力なモデルの予測を示しています。現在、この予測は常に 0 です。
- 2 番目のプロットは、弱いモデルのラベルであるエラーを示しています。
- 3 つ目のプロットは弱いモデルを示しています。
最初の弱いモデルはラベルの粗い表現を学習し、主に特徴空間の左側(変化が最も大きい部分であり、常に間違ったモデルでエラーが最も多い部分)に焦点を当てます。
アルゴリズムの別の反復処理の同じプロットは次のとおりです。
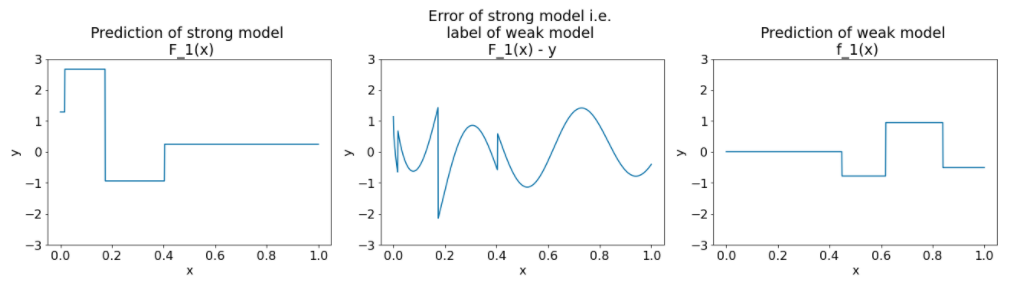
図 27. 2 回目の反復処理後の 3 つのプロット。
図 27 のグラフについて、次の点に注意してください。
- 強力なモデルには、前の反復処理の弱いモデルの予測が含まれるようになりました。
- 強力なモデルの新しいエラーは少し小さくなっています。
- 弱いモデルの新しい予測は、特徴空間の右側に焦点を当てています。
アルゴリズムをさらに 8 回反復します。
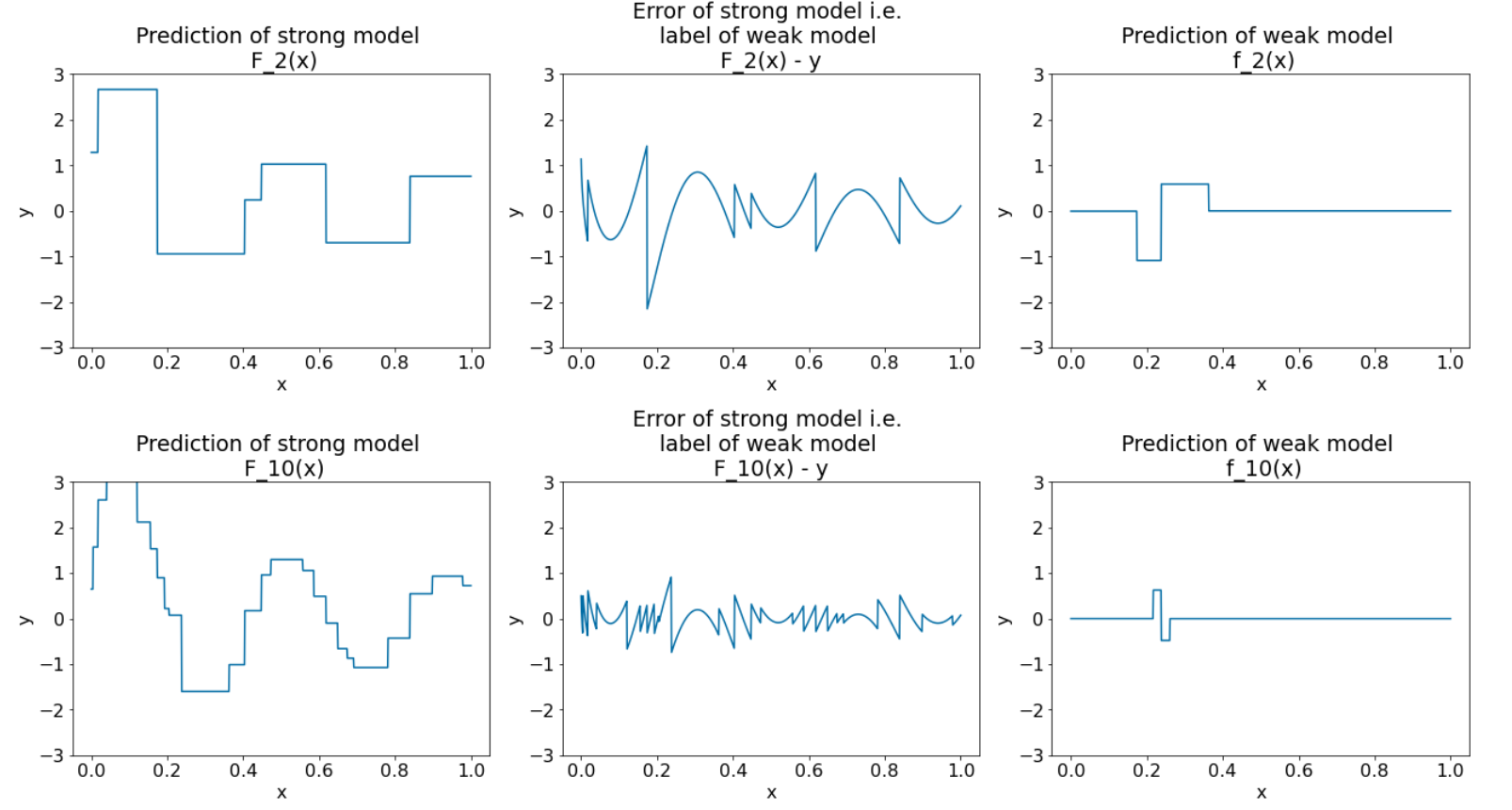
図 28. 3 回目の反復と 10 回目の反復後の 3 つのプロット。
図 28 では、強力なモデルの予測がデータセットのプロットに似ていることがわかります。
次の図は、ディシジョン ツリーを弱い学習者として使用する勾配ブースト アルゴリズムを示しています。この組み合わせは、勾配ブースト(ディシジョン)ツリーと呼ばれます。
上のグラフは、勾配ブーストの本質を示しています。ただし、この例には、次の 2 つの実際のオペレーションがありません。
- 縮み
- ニュートン法の 1 ステップによるリーフ値の最適化
収縮
弱いモデル $f_i$ は、小さな値 $\nu$(例: $\nu = 0.1$)を掛けた後に、強いモデル $F_i$ に追加されます。この小さな値は「縮小」と呼ばれます。つまり、各反復処理で次の式を使用するのではなく、
\[ F_{i+1} = F_i - f_i \]
各反復処理では、次の式を使用します。
\[ F_{i+1} = F_i - \nu f_i \]
勾配ブーストの縮小は、ニューラル ネットワークの学習率に似ています。縮小は、強力なモデルの学習速度を制御し、過剰適合を制限します。つまり、収縮値が 0.0 に近いほど、収縮値が 1.0 に近い場合よりも過剰適合が軽減されます。
上記のコードでは、収縮は次のように実装されます。
shrinkage = 0.1 # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions
