Assim como o bagging e o boosting, o gradient boosting é uma metodologia aplicada em cima de outro algoritmo de aprendizado de máquina. Informalmente, o aprimoramento por gradiente envolve dois tipos de modelos:
- um modelo de machine learning "fraco", que geralmente é uma árvore de decisão.
- um modelo de machine learning "forte", composto por vários modelos fracos.
No aumento gradual, em cada etapa, um novo modelo fraco é treinado para prever o "erro" do modelo forte atual, que é chamado de pseudoresposta. Vamos detalhar o "erro" mais adiante. Por enquanto, vamos supor que "erro" seja a diferença entre a previsão e um rótulo regressivo. O modelo fraco (ou seja, o "erro") é adicionado ao modelo forte com um sinal negativo para reduzir o erro do modelo forte.
O aumento do gradiente é iterativo. Cada iteração invoca a seguinte fórmula:
\[ F_{i+1} = F_i - f_i \]
em que:
- $F_i$ é o modelo forte na etapa $i$.
- $f_i$ é o modelo fraco na etapa $i$.
Essa operação se repete até que um critério de interrupção seja atendido, como um número máximo de iterações ou se o modelo (forte) começar a se ajustar em excesso, conforme medido em um conjunto de dados de validação separado.
Vamos ilustrar o aumento de gradiente em um conjunto de dados de regressão simples em que:
- O objetivo é prever $y$ a partir de $x$.
- O modelo forte é inicializado como uma constante zero: $F_0(x) = 0$.
# Simplified example of regressive gradient boosting.
y = ... # the labels
x = ... # the features
strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.
for i in range(num_iters):
# Error of the strong model
error = strong_predictions - y
# The weak model is a decision tree (see CART chapter)
# without pruning and a maximum depth of 3.
weak_model = tfdf.keras.CartModel(
task=tfdf.keras.Task.REGRESSION,
validation_ratio=0.0,
max_depth=3)
weak_model.fit(x=x, y=error)
strong_model.append(weak_model)
weak_predictions = weak_model.predict(x)[:,0]
strong_predictions -= weak_predictions
Vamos aplicar esse código ao seguinte conjunto de dados:

Figura 25. Um conjunto de dados regressivos sintéticos com um atributo numérico.
Aqui estão três gráficos após a primeira iteração do algoritmo de aprimoramento por gradiente:
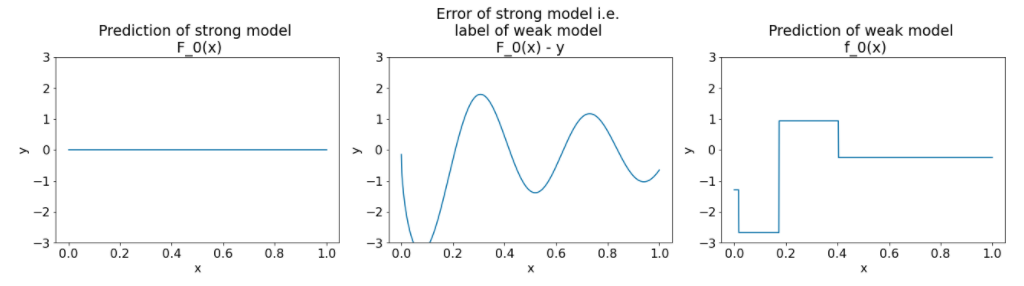
Figura 26. Três gráficos após a primeira iteração.
Observe o seguinte sobre os gráficos na Figura 26:
- O primeiro gráfico mostra as previsões do modelo forte, que atualmente é sempre 0.
- O segundo gráfico mostra o erro, que é o rótulo do modelo fraco.
- O terceiro gráfico mostra o modelo fraco.
O primeiro modelo fraco está aprendendo uma representação grosseira do rótulo e se concentra principalmente na parte esquerda do espaço de recursos (a parte com mais variação e, portanto, com mais erros para o modelo errado constante).
Confira a seguir os mesmos gráficos para outra iteração do algoritmo:
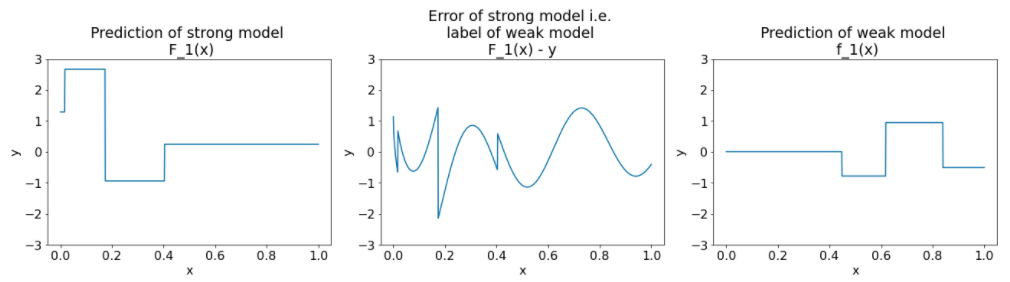
Figura 27. Três gráficos após a segunda iteração.
Observe o seguinte sobre os gráficos na Figura 27:
- O modelo forte agora contém a previsão do modelo fraco da iteração anterior.
- O novo erro do modelo forte é um pouco menor.
- A nova previsão do modelo fraco agora se concentra na parte direita do espaço de recursos.
Executamos o algoritmo para mais 8 iterações:
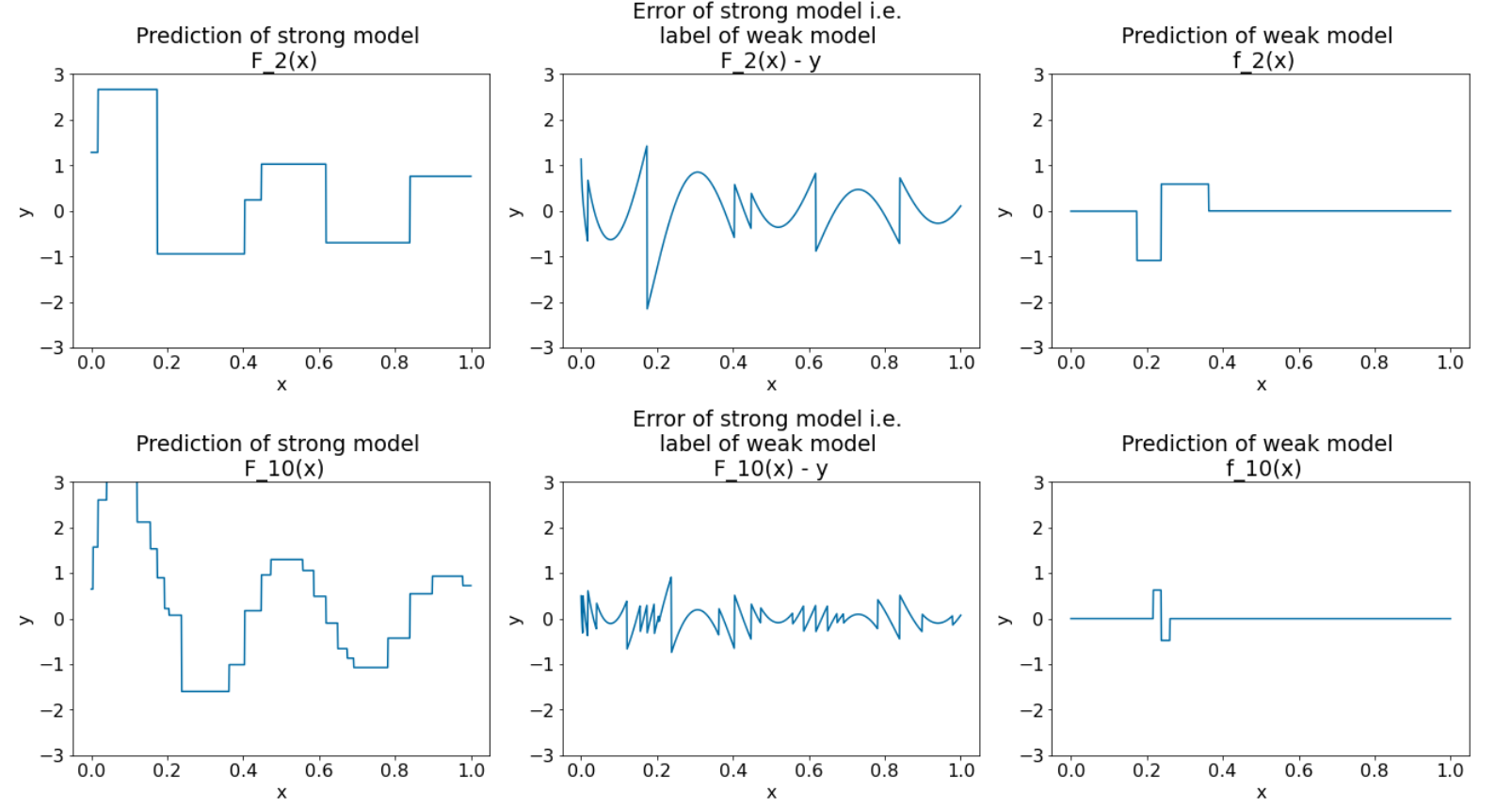
Figura 28. Três gráficos após a terceira e a décima iteração.
Na Figura 28, observe que a previsão do modelo forte começa a se parecer com o gráfico do conjunto de dados.
Estas figuras ilustram o algoritmo de intensificação por gradiente usando árvores de decisão como aprendizes fracos. Essa combinação é chamada de árvores (de decisão) aprimoradas por gradiente.
Os gráficos anteriores sugerem a essência do boosting por gradiente. No entanto, este exemplo não tem as duas operações reais a seguir:
- O encolhimento
- A otimização de valores de folhas com uma etapa do método de Newton
Encolhimento
O modelo fraco $f_i$ é multiplicado por um valor pequeno $\nu$ (por exemplo, $\nu = 0,1$) antes de ser adicionado ao modelo forte $F_i$. Esse valor pequeno é chamado de encolhimento. Em outras palavras, em vez de cada iteração usar a seguinte fórmula:
\[ F_{i+1} = F_i - f_i \]
Cada iteração usa a seguinte fórmula:
\[ F_{i+1} = F_i - \nu f_i \]
A redução no aumento de gradiente é análoga à taxa de aprendizado em redes neurais. A redução controla a rapidez com que o modelo forte está aprendendo, o que ajuda a limitar a superadaptação. Ou seja, um valor de encolhimento mais próximo de 0,0 reduz a superadaptação mais do que um valor de encolhimento mais próximo de 1,0.
No código acima, a redução seria implementada da seguinte maneira:
shrinkage = 0.1 # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions
