Paketleme ve güçlendirme gibi gradyan güçlendirme de başka bir makine öğrenimi algoritmasının üzerine uygulanan bir yöntemdir. Eğim artırma, iki tür model içerir:
- genellikle bir karar ağacı olan "zayıf" bir makine öğrenimi modeli
- birden fazla zayıf modelden oluşan "güçlü" bir makine öğrenimi modeli
Gradyan artırmada her adımda, mevcut güçlü modelin "hatasını" (sözde yanıt olarak adlandırılır) tahmin etmek için yeni bir zayıf model eğitilir. "Hata"yı daha sonra ayrıntılı olarak açıklayacağız. Şimdilik "hata"nın tahmin ile geriye dönük bir etiket arasındaki fark olduğunu varsayalım. Ardından zayıf model ("hata"), güçlü modelin hatasını azaltmak için güçlü modele eksi işaretiyle eklenir.
Gradyan güçlendirme yinelemeli bir işlemdir. Her iterasyon aşağıdaki formülü çağırır:
\[ F_{i+1} = F_i - f_i \]
Bu örnekte:
- $F_i$, $i$. adımdaki güçlü modeldir.
- $f_i$, $i$. adımdaki zayıf modeldir.
Bu işlem, maksimum iterasyon sayısı gibi bir durdurma ölçütü karşılanana veya (güçlü) model ayrı bir doğrulama veri kümesinde ölçüldüğü üzere aşırı uyum sağlamaya başlayana kadar tekrarlanır.
Aşağıdaki basit regresyon veri kümesinde gradyan artırmayı gösterelim:
- Amaç, $x$ değerinden $y$ değerini tahmin etmektir.
- Güçlü model, sıfır sabit olarak başlatılır: $F_0(x) = 0$.
# Simplified example of regressive gradient boosting.
y = ... # the labels
x = ... # the features
strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.
for i in range(num_iters):
# Error of the strong model
error = strong_predictions - y
# The weak model is a decision tree (see CART chapter)
# without pruning and a maximum depth of 3.
weak_model = tfdf.keras.CartModel(
task=tfdf.keras.Task.REGRESSION,
validation_ratio=0.0,
max_depth=3)
weak_model.fit(x=x, y=error)
strong_model.append(weak_model)
weak_predictions = weak_model.predict(x)[:,0]
strong_predictions -= weak_predictions
Bu kodu aşağıdaki veri kümesine uygulayalım:
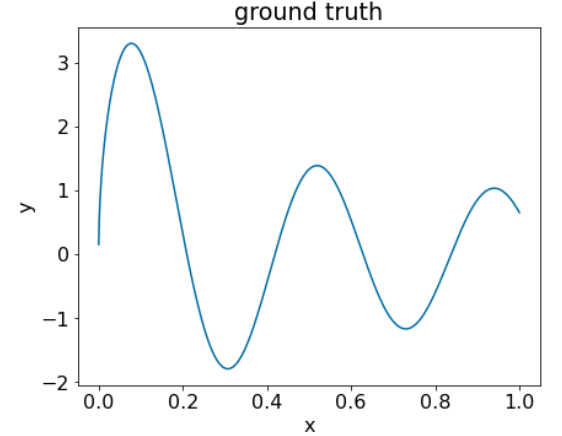
Şekil 25. Bir sayısal özelliğe sahip sentetik regresif veri kümesi.
Gradyan artırma algoritmasının ilk iterasyonundan sonra üç nokta grafiği gösterilmektedir:
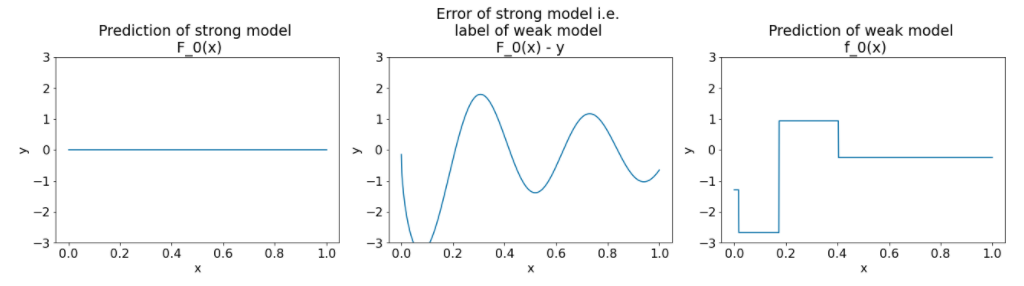
Şekil 26. İlk iterasyondan sonra üç nokta.
Şekil 26'daki noktalarla ilgili aşağıdakilere dikkat edin:
- İlk çizim, güçlü modelin tahminlerini gösterir. Bu tahminler şu anda her zaman 0'dır.
- İkinci grafikte, zayıf modelin etiketi olan hata gösterilir.
- Üçüncü grafikte zayıf model gösterilmektedir.
İlk zayıf model, etiketin kaba bir temsilini öğrenir ve çoğunlukla özellik alanının sol kısmına (en fazla varyasyona sahip olan ve dolayısıyla sürekli yanlış model için en fazla hataya sahip olan kısım) odaklanır.
Aşağıda, algoritmanın başka bir iterasyonu için aynı grafikler verilmiştir:
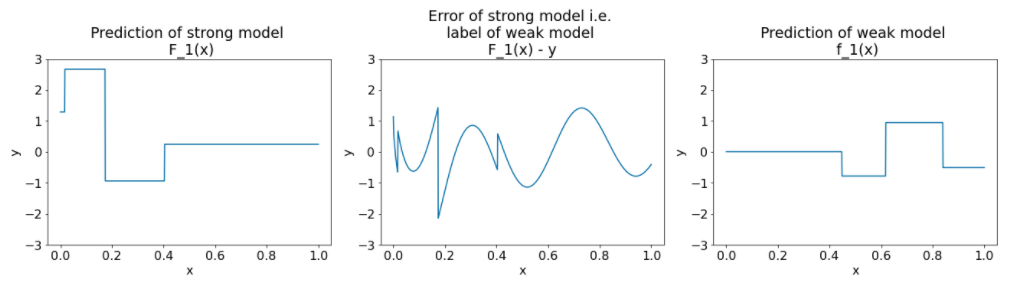
Şekil 27. İkinci iterasyondan sonra üç nokta.
Şekil 27'deki noktalarla ilgili aşağıdakilere dikkat edin:
- Güçlü model artık önceki iterasyonun zayıf modelinin tahminini içerir.
- Güçlü modelin yeni hatası biraz daha küçük.
- Zayıf modelin yeni tahmini artık özellik alanının sağ tarafına odaklanıyor.
Algoritmayı 8 iterasyon daha çalıştırırız:
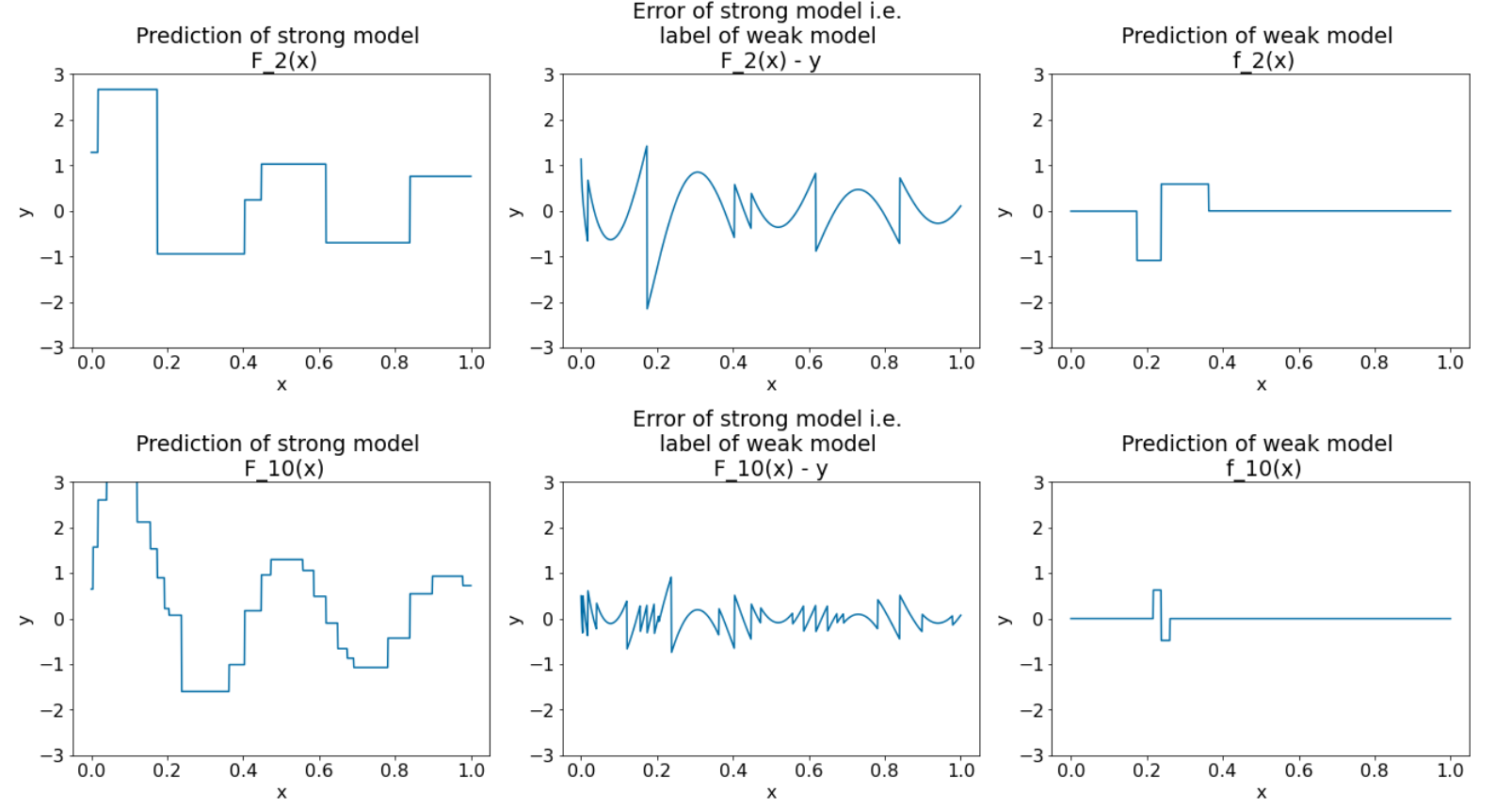
Şekil 28. Üçüncü iterasyondan ve onuncu iterasyondan sonra üç nokta.
Şekil 28'de, güçlü modelin tahmininin veri kümesinin grafiğine benzemeye başladığını görebilirsiniz.
Bu şekiller, zayıf öğrenenler olarak karar ağaçlarını kullanan gradyan artırma algoritmasını göstermektedir. Bu kombinasyona gradyan artırmalı (karar) ağaçlar denir.
Önceki grafikler, gradyan güçlendirmenin özünü göstermektedir. Ancak bu örnekte, gerçek dünyadaki aşağıdaki iki işlem eksiktir:
- Küçülme
- Newton yönteminin bir adımı kullanılarak yaprak değerlerinin optimizasyonu
Küçülme
Zayıf model $f_i$, güçlü model $F_i$'ye eklenmeden önce küçük bir değerle ($\nu$) çarpılır (ör.$\nu = 0,1$). Bu küçük değere küçültme adı verilir. Başka bir deyişle, her iterasyonda aşağıdaki formülü kullanmak yerine:
\[ F_{i+1} = F_i - f_i \]
Her iterasyonda aşağıdaki formül kullanılır:
\[ F_{i+1} = F_i - \nu f_i \]
Gradyan güçlendirmedeki küçülme, nöral ağlardaki öğrenme hızına benzer. Küçültme, güçlü modelin ne kadar hızlı öğrendiğini kontrol eder ve bu da aşırı uyumu sınırlamaya yardımcı olur. Yani, 0,0'a yakın bir küçülme değeri, 1,0'a yakın bir küçülme değerinden daha fazla aşırı uyumu azaltır.
Yukarıdaki kodumuzda, sıkıştırma aşağıdaki şekilde uygulanır:
shrinkage = 0.1 # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions
