مثل أسلوبَي "التجميع" و"الترقية"، فإنّ أسلوب "ترقية التدرّج" هو منهج يتم تطبيقه على خوارزمية تعلُّم آلي أخرى. بشكل غير رسمي، تشمل تعزيز التدرّج نوعَين من النماذج:
- نموذج تعلُّم آلي "ضعيف"، وهو عادةً شجرة قرارات
- نموذج "قوي" للتعلم الآلي، وهو يتألف من نماذج ضعيفة متعددة
في أسلوب "التعزيز التدرّجي"، يتم تدريب نموذج جديد منخفض الدقة في كل خطوة لتوقّع "الخطأ" في النموذج القوي الحالي (الذي يُعرف باسم الردّ الزائف). سنوضّح معنى "الخطأ" لاحقًا. لنفترض الآن أنّ "الخطأ" هو الفرق بين التوقّع والعلامة التنازلية. تتم بعد ذلك إضافة النموذج الضعيف (أي "الخطأ") إلى النموذج القوي مع علامة سلبية لتقليل خطأ النموذج القوي.
التعزيز الاشتقاقي هو عملية متكرّرة. تستدعي كلّ تكرار الصيغة التالية:
\[ F_{i+1} = F_i - f_i \]
حيث:
- $F_i$ هو النموذج القوي في الخطوة $i$.
- $f_i$ هو النموذج الضعيف في الخطوة $i$.
تتكرر هذه العملية إلى أن يتم استيفاء معيار التوقف، مثل الحد الأقصى لعدد التكرارات أو إذا بدأ النموذج (القوي) في التكيّف المفرط كما تم قياسه في مجموعة بيانات التحقّق المنفصلة.
لنوضّح أسلوب "التعزيز التدرّجي" على مجموعة بيانات انحدار بسيطة حيث:
- الهدف هو توقّع $y$ من $x$.
- يتمّ إعداد النموذج القوي ليكون ثابتًا يساوي صفرًا: $F_0(x) = 0$.
# Simplified example of regressive gradient boosting.
y = ... # the labels
x = ... # the features
strong_model = []
strong_predictions = np.zeros_like(y) # Initially, the strong model is empty.
for i in range(num_iters):
# Error of the strong model
error = strong_predictions - y
# The weak model is a decision tree (see CART chapter)
# without pruning and a maximum depth of 3.
weak_model = tfdf.keras.CartModel(
task=tfdf.keras.Task.REGRESSION,
validation_ratio=0.0,
max_depth=3)
weak_model.fit(x=x, y=error)
strong_model.append(weak_model)
weak_predictions = weak_model.predict(x)[:,0]
strong_predictions -= weak_predictions
لنطبّق هذا الرمز على مجموعة البيانات التالية:
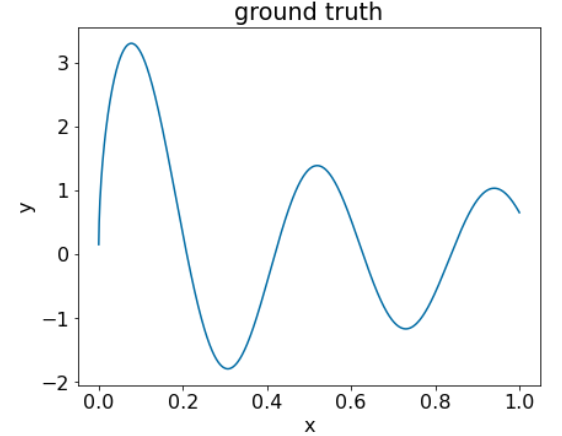
الشكل 25: مجموعة بيانات اصطناعية للانحدار تحتوي على سمة رقمية واحدة
في ما يلي ثلاث رسوم بيانية بعد التكرار الأول من أسلوب الصعُود التدرّجي للتصنيف:
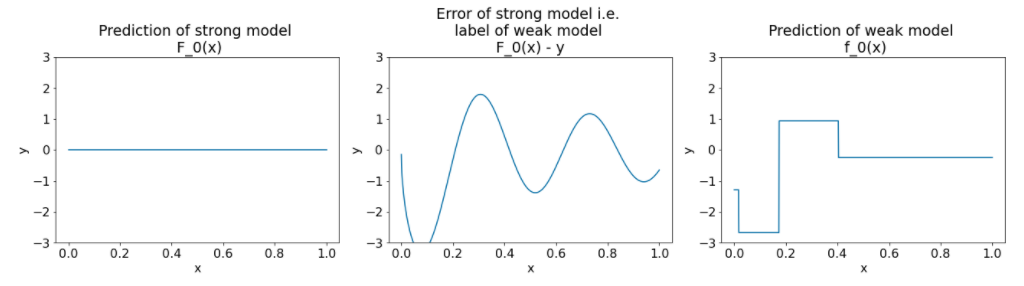
الشكل 26. ثلاث رسوم بيانية بعد التكرار الأول
يُرجى ملاحظة ما يلي بشأن الرسوم البيانية في الشكل 26:
- تعرِض الرسمة البيانية الأولى توقّعات النموذج القوي، والتي هي حاليًا 0 دائمًا.
- يعرض الرسم البياني الثاني الخطأ، وهو تصنيف النموذج الضعيف.
- يعرض الرسم البياني الثالث النموذج الضعيف.
يتعلم النموذج الضعيف الأول تمثيلًا فظًا للتصنيف ويركز في معظمه على الجزء الأيسر من مساحة العناصر (الجزء الذي يتضمّن أكبر قدر من الاختلاف، وبالتالي أكبر قدر من الأخطاء للنموذج الخاطئ الثابت).
في ما يلي الرسوم البيانية نفسها لتكرار آخر من الخوارزمية:
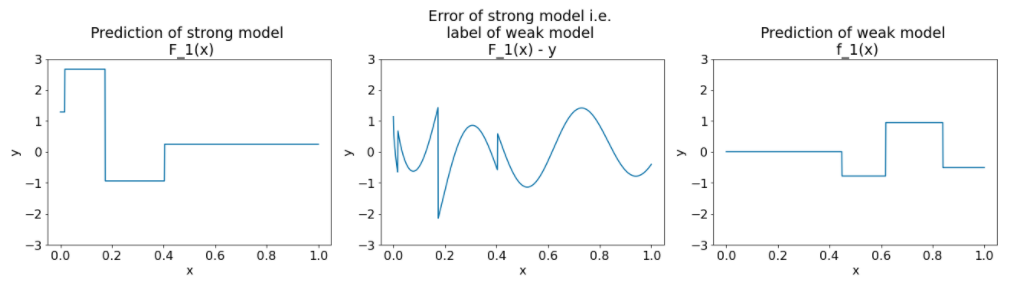
الشكل 27. ثلاث مقاطع بعد التكرار الثاني
يُرجى ملاحظة ما يلي بشأن الرسوم البيانية في الشكل 27:
- يتضمّن النموذج القوي الآن توقّعات النموذج الضعيف في المحاولة السابقة.
- الخطأ الجديد للنموذج القوي أصغر قليلاً.
- يركز التوقّع الجديد للنموذج الضعيف الآن على الجزء الأيمن من مساحة السمات.
نُجري الخوارزمية 8 مرّات أخرى:
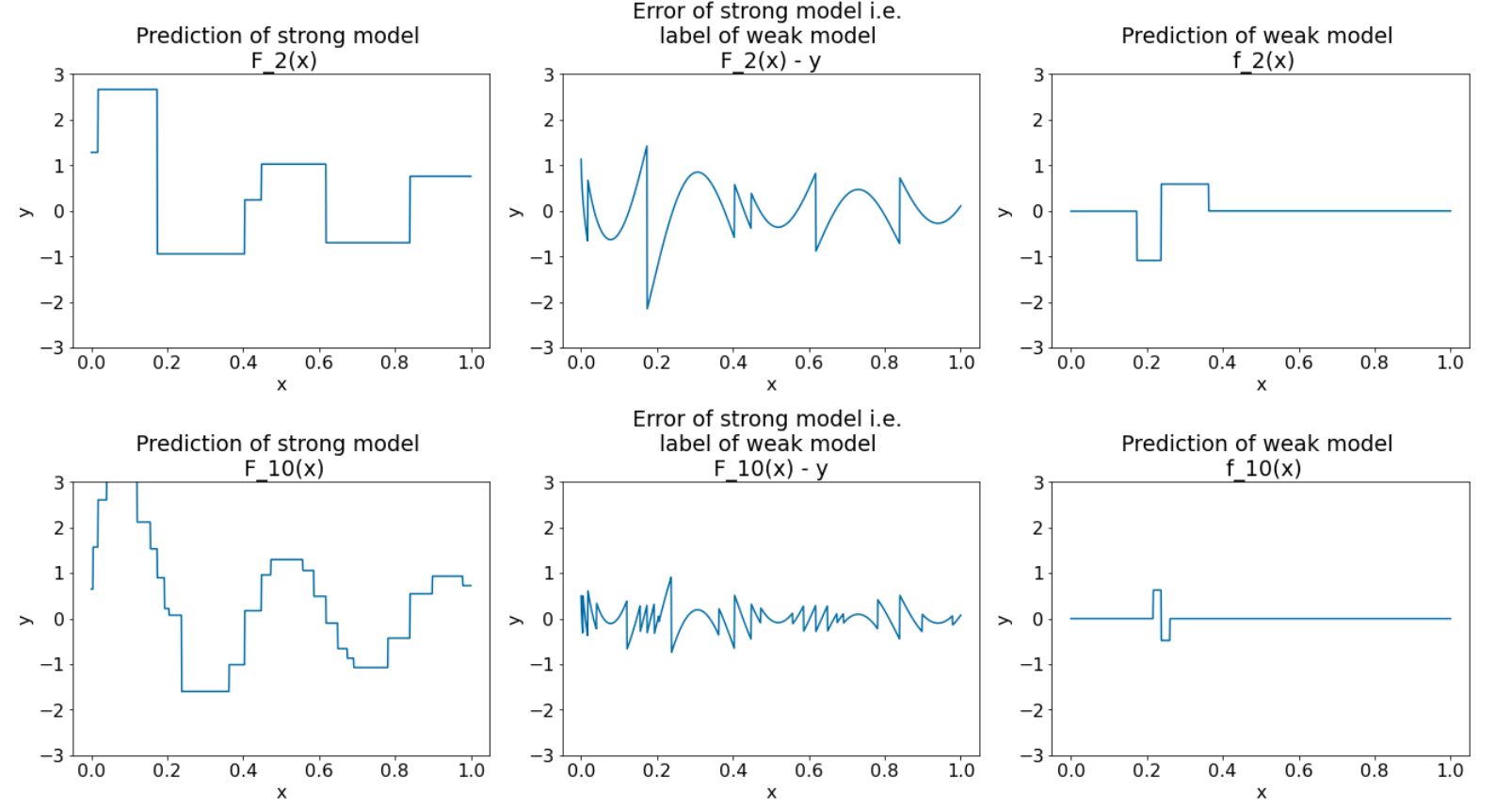
الشكل 28. ثلاث مقاطع بعد التكرار الثالث والتكرار العاشر
في الشكل 28، يُرجى ملاحظة أنّ توقّعات النموذج القوي تبدأ في التشابه مع مخطّط مجموعة البيانات.
توضِّح هذه الأشكال خوارزمية تقوية التدرّج باستخدام أشجار القرارات بصفتها مدرّبين ضعيفين. يُعرف هذا المزيج باسم الأشجار (القرارية) المحسَّنة باستخدام التدرّج.
تشير الرسوم البيانية السابقة إلى جوهر تحسين التدرّج. ومع ذلك، يفتقر هذا المثال إلى العمليتين التاليتَين في العالم الواقعي:
- التقلّص
- تحسين قيم الأوراق باستخدام خطوة واحدة من طريقة نيوتن
التقلّص
يتم ضرب النموذج الضعيف $f_i$ في قيمة صغيرة $\nu$ (على سبيل المثال، $\nu = 0.1$) قبل إضافته إلى النموذج القوي $F_i$. وتُعرف هذه القيمة الصغيرة باسم الانكماش. بعبارة أخرى، بدلاً من استخدام كل تكرار للمعادلة التالية:
\[ F_{i+1} = F_i - f_i \]
تستخدِم كلّ خطوة من الخطوات الصيغة التالية:
\[ F_{i+1} = F_i - \nu f_i \]
إنّ التقلّص في تحسين التدرّج مشابه لمعدل التعلّم في الشبكات العصبية. يتحكّم الانكماش في سرعة تعلُّم النموذج القوي، ما يساعد في الحدّ من الملاءمة الزائدة. وهذا يعني أنّ قيمة الانكماش الأقرب إلى 0.0 تقلّل من التكيّف المفرط أكثر مقارنةً بقيمة الانكماش الأقرب إلى 1.0.
في الرمز البرمجي أعلاه، سيتم تنفيذ عملية التصغير على النحو التالي:
shrinkage = 0.1 # 0.1 is a common shrinkage value.
strong_predictions -= shrinkage * weak_predictions
